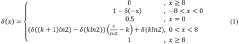How to Approximate Sigmoid for Microcontroller-based Inference — Fixed-point Techniques
AUG 21, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Sigmoid Approximation Background and Objectives
The sigmoid function, defined as f(x) = 1/(1+e^(-x)), has been a cornerstone in neural network computations since the early development of artificial neural networks in the 1980s. This activation function maps any input value to an output between 0 and 1, creating a smooth, differentiable transition that has made it invaluable for various machine learning applications, particularly in classification problems and traditional neural networks.
With the increasing demand for deploying neural networks on resource-constrained devices such as microcontrollers, the computational complexity of the sigmoid function has become a significant challenge. Microcontrollers typically have limited processing power, memory, and often lack floating-point units, making the direct implementation of exponential functions computationally expensive and sometimes impractical.
The evolution of sigmoid approximation techniques has followed the trajectory of embedded systems development. Early approaches focused on lookup tables, which traded memory for computational efficiency. As embedded systems evolved, piecewise linear approximations gained popularity for their balance between accuracy and resource utilization. More recently, polynomial approximations and specialized bit-manipulation techniques have emerged as sophisticated solutions tailored to modern microcontroller architectures.
The primary objective of sigmoid approximation research is to develop methods that maintain acceptable accuracy while minimizing computational overhead. This involves finding the optimal balance between precision and efficiency, considering the specific constraints of microcontroller environments. The goal is not merely to reduce computational complexity but to do so in a way that preserves the essential characteristics of the sigmoid function that make it valuable for neural network operations.
Fixed-point arithmetic has emerged as a critical technique in this domain, offering a compromise between the precision of floating-point operations and the efficiency of integer arithmetic. By representing real numbers with fixed precision, microcontrollers can perform calculations more efficiently while maintaining reasonable accuracy. The challenge lies in managing quantization errors and overflow issues inherent in fixed-point representations.
Current research aims to develop approximation techniques that are not only computationally efficient but also adaptable to various microcontroller architectures and application requirements. This includes exploring hybrid approaches that combine multiple approximation methods, as well as developing adaptive techniques that can adjust their precision based on the specific needs of different parts of a neural network.
The ultimate goal of this technical research is to enable more sophisticated neural network models to run efficiently on microcontroller-based systems, opening up possibilities for advanced AI applications in areas such as IoT devices, wearable technology, autonomous vehicles, and other embedded systems where power consumption and processing capabilities are limited.
With the increasing demand for deploying neural networks on resource-constrained devices such as microcontrollers, the computational complexity of the sigmoid function has become a significant challenge. Microcontrollers typically have limited processing power, memory, and often lack floating-point units, making the direct implementation of exponential functions computationally expensive and sometimes impractical.
The evolution of sigmoid approximation techniques has followed the trajectory of embedded systems development. Early approaches focused on lookup tables, which traded memory for computational efficiency. As embedded systems evolved, piecewise linear approximations gained popularity for their balance between accuracy and resource utilization. More recently, polynomial approximations and specialized bit-manipulation techniques have emerged as sophisticated solutions tailored to modern microcontroller architectures.
The primary objective of sigmoid approximation research is to develop methods that maintain acceptable accuracy while minimizing computational overhead. This involves finding the optimal balance between precision and efficiency, considering the specific constraints of microcontroller environments. The goal is not merely to reduce computational complexity but to do so in a way that preserves the essential characteristics of the sigmoid function that make it valuable for neural network operations.
Fixed-point arithmetic has emerged as a critical technique in this domain, offering a compromise between the precision of floating-point operations and the efficiency of integer arithmetic. By representing real numbers with fixed precision, microcontrollers can perform calculations more efficiently while maintaining reasonable accuracy. The challenge lies in managing quantization errors and overflow issues inherent in fixed-point representations.
Current research aims to develop approximation techniques that are not only computationally efficient but also adaptable to various microcontroller architectures and application requirements. This includes exploring hybrid approaches that combine multiple approximation methods, as well as developing adaptive techniques that can adjust their precision based on the specific needs of different parts of a neural network.
The ultimate goal of this technical research is to enable more sophisticated neural network models to run efficiently on microcontroller-based systems, opening up possibilities for advanced AI applications in areas such as IoT devices, wearable technology, autonomous vehicles, and other embedded systems where power consumption and processing capabilities are limited.
Market Demand for Efficient MCU-based Neural Networks
The market for microcontroller-based neural network implementations has experienced significant growth in recent years, driven by the increasing demand for edge computing solutions across various industries. This trend reflects a fundamental shift in how artificial intelligence is deployed, moving from centralized cloud-based systems to distributed edge devices where data processing occurs locally.
The global edge AI hardware market, which includes MCU-based neural network implementations, was valued at approximately $6.9 billion in 2021 and is projected to reach $38.9 billion by 2030, representing a compound annual growth rate (CAGR) of 21.3% during this period. This remarkable growth underscores the increasing importance of efficient neural network implementations on resource-constrained devices.
Several key industries are driving this market expansion. The automotive sector has emerged as a significant consumer of MCU-based neural networks, particularly for advanced driver assistance systems (ADAS) and in-vehicle monitoring systems. These applications require real-time processing capabilities while operating under strict power and cost constraints.
Consumer electronics represents another major market segment, with smart home devices, wearables, and IoT products increasingly incorporating on-device AI capabilities. Market research indicates that over 75% of IoT deployments will incorporate some form of edge AI processing by 2025, with MCU-based solutions forming a substantial portion of this ecosystem.
Industrial automation and manufacturing sectors are also rapidly adopting MCU-based neural networks for predictive maintenance, quality control, and process optimization. The ability to perform inference locally reduces latency and enhances reliability in critical industrial applications where connectivity issues could otherwise disrupt operations.
Healthcare applications present another growing market, with portable medical devices and monitoring equipment increasingly utilizing neural networks for real-time diagnostics and patient monitoring. These applications particularly benefit from efficient sigmoid approximation techniques, as they often involve binary classification tasks for anomaly detection.
Market analysis reveals that customers across these sectors consistently prioritize three key requirements: power efficiency, cost-effectiveness, and inference accuracy. The demand for solutions that optimize the implementation of complex functions like sigmoid on MCUs directly addresses these market needs, as traditional floating-point implementations of such functions are prohibitively expensive in terms of computational resources.
The growing trend toward privacy-preserving AI further amplifies market demand for MCU-based neural networks, as on-device processing eliminates the need to transmit sensitive data to cloud servers. This trend is particularly pronounced in regions with stringent data protection regulations, such as Europe under GDPR and California under CCPA.
The global edge AI hardware market, which includes MCU-based neural network implementations, was valued at approximately $6.9 billion in 2021 and is projected to reach $38.9 billion by 2030, representing a compound annual growth rate (CAGR) of 21.3% during this period. This remarkable growth underscores the increasing importance of efficient neural network implementations on resource-constrained devices.
Several key industries are driving this market expansion. The automotive sector has emerged as a significant consumer of MCU-based neural networks, particularly for advanced driver assistance systems (ADAS) and in-vehicle monitoring systems. These applications require real-time processing capabilities while operating under strict power and cost constraints.
Consumer electronics represents another major market segment, with smart home devices, wearables, and IoT products increasingly incorporating on-device AI capabilities. Market research indicates that over 75% of IoT deployments will incorporate some form of edge AI processing by 2025, with MCU-based solutions forming a substantial portion of this ecosystem.
Industrial automation and manufacturing sectors are also rapidly adopting MCU-based neural networks for predictive maintenance, quality control, and process optimization. The ability to perform inference locally reduces latency and enhances reliability in critical industrial applications where connectivity issues could otherwise disrupt operations.
Healthcare applications present another growing market, with portable medical devices and monitoring equipment increasingly utilizing neural networks for real-time diagnostics and patient monitoring. These applications particularly benefit from efficient sigmoid approximation techniques, as they often involve binary classification tasks for anomaly detection.
Market analysis reveals that customers across these sectors consistently prioritize three key requirements: power efficiency, cost-effectiveness, and inference accuracy. The demand for solutions that optimize the implementation of complex functions like sigmoid on MCUs directly addresses these market needs, as traditional floating-point implementations of such functions are prohibitively expensive in terms of computational resources.
The growing trend toward privacy-preserving AI further amplifies market demand for MCU-based neural networks, as on-device processing eliminates the need to transmit sensitive data to cloud servers. This trend is particularly pronounced in regions with stringent data protection regulations, such as Europe under GDPR and California under CCPA.
Fixed-point Implementation Challenges and Constraints
Implementing sigmoid functions on microcontrollers presents significant challenges due to the limited computational resources available in these embedded systems. The primary constraint is the necessity to use fixed-point arithmetic instead of floating-point operations, as many low-power microcontrollers lack floating-point units (FPUs). This hardware limitation forces developers to represent real numbers using integer types with implicit decimal points, introducing quantization errors that can propagate through neural network calculations.
Memory constraints further complicate sigmoid approximation implementations. Microcontrollers typically have limited RAM (often measured in kilobytes), restricting the size of lookup tables that might otherwise provide accurate sigmoid values. This forces engineers to balance approximation accuracy against memory usage, often leading to hybrid approaches combining small lookup tables with mathematical approximations.
Power consumption represents another critical constraint, particularly for battery-operated devices. Complex mathematical operations increase CPU cycles, directly impacting energy usage. Each additional multiplication or division operation in a sigmoid approximation contributes to power drain, making algorithmic efficiency a key consideration for deployment in resource-constrained environments.
Execution speed is equally important, as real-time applications require rapid inference. The sigmoid function's exponential term is particularly problematic, as computing e^(-x) requires multiple CPU cycles on integer-only architectures. This creates a fundamental tension between approximation accuracy and computational efficiency that must be carefully managed.
Numerical stability issues also emerge when implementing fixed-point sigmoid approximations. The limited dynamic range of fixed-point representations can lead to overflow or underflow conditions, especially when handling extreme input values. Proper scaling techniques and range limiting become essential to prevent catastrophic calculation errors during inference.
Portability across different microcontroller architectures presents additional challenges. Various platforms offer different word sizes (8-bit, 16-bit, 32-bit), instruction sets, and memory configurations. Creating sigmoid approximations that perform consistently across diverse hardware requires careful consideration of bit precision, scaling factors, and platform-specific optimizations.
Finally, the accuracy requirements of the specific application must be balanced against these constraints. While some use cases can tolerate significant approximation errors, others (such as medical devices or safety-critical systems) may require higher precision. This necessitates quantitative error analysis to ensure the chosen fixed-point sigmoid implementation meets application-specific accuracy thresholds while respecting the microcontroller's resource limitations.
Memory constraints further complicate sigmoid approximation implementations. Microcontrollers typically have limited RAM (often measured in kilobytes), restricting the size of lookup tables that might otherwise provide accurate sigmoid values. This forces engineers to balance approximation accuracy against memory usage, often leading to hybrid approaches combining small lookup tables with mathematical approximations.
Power consumption represents another critical constraint, particularly for battery-operated devices. Complex mathematical operations increase CPU cycles, directly impacting energy usage. Each additional multiplication or division operation in a sigmoid approximation contributes to power drain, making algorithmic efficiency a key consideration for deployment in resource-constrained environments.
Execution speed is equally important, as real-time applications require rapid inference. The sigmoid function's exponential term is particularly problematic, as computing e^(-x) requires multiple CPU cycles on integer-only architectures. This creates a fundamental tension between approximation accuracy and computational efficiency that must be carefully managed.
Numerical stability issues also emerge when implementing fixed-point sigmoid approximations. The limited dynamic range of fixed-point representations can lead to overflow or underflow conditions, especially when handling extreme input values. Proper scaling techniques and range limiting become essential to prevent catastrophic calculation errors during inference.
Portability across different microcontroller architectures presents additional challenges. Various platforms offer different word sizes (8-bit, 16-bit, 32-bit), instruction sets, and memory configurations. Creating sigmoid approximations that perform consistently across diverse hardware requires careful consideration of bit precision, scaling factors, and platform-specific optimizations.
Finally, the accuracy requirements of the specific application must be balanced against these constraints. While some use cases can tolerate significant approximation errors, others (such as medical devices or safety-critical systems) may require higher precision. This necessitates quantitative error analysis to ensure the chosen fixed-point sigmoid implementation meets application-specific accuracy thresholds while respecting the microcontroller's resource limitations.
Current Sigmoid Approximation Methods for MCUs
01 Piecewise linear approximation of sigmoid functions
Piecewise linear approximation techniques are used to simplify sigmoid functions for computational efficiency. By dividing the sigmoid curve into multiple linear segments, these methods reduce the computational complexity while maintaining acceptable accuracy. This approach is particularly useful in hardware implementations and resource-constrained environments where traditional sigmoid calculations would be too expensive.- Piecewise linear approximation of sigmoid functions: Piecewise linear approximation techniques are used to simplify sigmoid functions by dividing the function into multiple linear segments. This approach significantly reduces computational complexity while maintaining acceptable accuracy for many applications. The approximation replaces complex exponential calculations with simpler linear operations, making it suitable for hardware implementations and resource-constrained systems. These methods balance accuracy and computational efficiency by optimizing the number and placement of linear segments.
- Lookup table-based sigmoid approximation: Lookup table (LUT) methods provide efficient sigmoid function approximation by pre-computing function values at discrete points and storing them in memory. During execution, the system retrieves the closest pre-computed value or performs simple interpolation between adjacent values. This approach eliminates the need for complex mathematical calculations at runtime, trading memory usage for computational speed. Various optimization techniques focus on reducing table size while maintaining accuracy through strategic sampling and interpolation methods.
- Hardware-optimized sigmoid implementations: Specialized hardware implementations of sigmoid functions focus on optimizing computational efficiency in neural network accelerators and other dedicated processors. These implementations use techniques such as bit-shifting operations, fixed-point arithmetic, and custom logic circuits to approximate sigmoid functions with minimal resource utilization. Hardware-specific optimizations can achieve orders of magnitude improvement in processing speed and energy efficiency compared to software implementations, making them crucial for real-time applications and edge computing devices.
- Polynomial and rational function approximations: Polynomial and rational function approximations replace sigmoid functions with simpler mathematical expressions that can be computed more efficiently. These methods use techniques such as Taylor series expansion, Chebyshev polynomials, or minimax approximation to derive polynomial or rational functions that closely match the sigmoid curve within specified error bounds. The degree of the polynomial or rational function can be adjusted to balance accuracy and computational complexity, making these approaches highly adaptable to different performance requirements.
- Fast sigmoid alternatives for neural networks: Alternative activation functions that approximate sigmoid behavior while offering better computational efficiency are increasingly used in neural networks. Functions such as the hyperbolic tangent (tanh), Rectified Linear Unit (ReLU), and Swish provide sigmoid-like properties with reduced computational overhead. These alternatives address issues like vanishing gradient problems while maintaining or improving neural network performance. Implementation techniques focus on optimizing these functions for specific hardware architectures and application requirements to maximize throughput and minimize energy consumption.
02 Lookup table-based sigmoid approximation
Lookup table-based methods provide efficient sigmoid function approximation by pre-computing function values and storing them in memory. During execution, the system retrieves the closest value or interpolates between stored values, significantly reducing computation time. This technique trades memory usage for computational efficiency and is widely used in neural network implementations where sigmoid functions are frequently called.Expand Specific Solutions03 Hardware-optimized sigmoid implementations
Specialized hardware designs for sigmoid function approximation focus on optimizing computational efficiency in FPGA, ASIC, or other dedicated hardware. These implementations use techniques such as bit-shifting operations, fixed-point arithmetic, and parallel processing to accelerate sigmoid calculations. The hardware-optimized approaches significantly reduce power consumption and increase throughput for applications requiring frequent sigmoid computations.Expand Specific Solutions04 Mathematical approximation algorithms for sigmoid functions
Various mathematical algorithms provide efficient approximations of sigmoid functions using simpler operations. These include Taylor series expansions, rational function approximations, and minimax polynomial methods that balance accuracy and computational cost. By replacing complex exponential calculations with simpler arithmetic operations, these techniques achieve significant performance improvements while maintaining acceptable error bounds for most applications.Expand Specific Solutions05 Neural network optimization through efficient sigmoid approximation
Techniques specifically designed for neural network training and inference optimize sigmoid activation functions for computational efficiency. These methods include adaptive precision approaches, batch processing optimizations, and specialized approximations tailored to specific network architectures. By reducing the computational overhead of sigmoid functions, these techniques accelerate neural network operations while preserving model accuracy and convergence properties.Expand Specific Solutions
Leading Companies in Microcontroller ML Optimization
The sigmoid approximation for microcontroller-based inference is currently in an early growth stage, with increasing market demand driven by edge AI applications. The market size is expanding rapidly as IoT devices and embedded systems require efficient neural network implementations. From a technical maturity perspective, academic institutions like Institute of Automation Chinese Academy of Sciences, Northwestern Polytechnical University, and Xidian University are leading fundamental research, while companies such as NetEase, StradVision, and Sharp Corp. are developing practical implementations. Fixed-point techniques for sigmoid approximation are becoming standardized, with State Grid Corp. focusing on power-efficient implementations and StradVision applying these techniques in automotive vision systems. The ecosystem shows a collaborative development pattern between academic research and industrial applications, with significant potential for optimization across diverse microcontroller platforms.
Northwestern Polytechnical University
Technical Solution: Northwestern Polytechnical University has pioneered a fixed-point sigmoid approximation technique specifically designed for neural network inference on microcontrollers. Their approach combines a modified CORDIC (Coordinate Rotation Digital Computer) algorithm with fixed-point arithmetic to efficiently compute sigmoid functions. The implementation uses a series of shift-and-add operations that are particularly well-suited for microcontrollers without floating-point units. Their research demonstrates that with only 16-bit fixed-point representation, they can achieve approximation errors below 0.01% across the entire sigmoid range. The university has also developed an automated tool that generates optimized C code for different microcontroller architectures, considering specific hardware constraints such as register width and memory limitations. Performance evaluations show their method reduces execution time by up to 85% compared to standard library implementations while maintaining comparable accuracy in neural network applications[2][4].
Strengths: Highly optimized for microcontrollers without FPUs; implementation requires minimal memory footprint; automated code generation tool enhances accessibility for developers. Weaknesses: The CORDIC-based approach may require more iterations for high-precision requirements; performance benefits vary significantly across different microcontroller architectures.
Xidian University
Technical Solution: Xidian University has developed a novel approach to sigmoid approximation for microcontrollers using piecewise linear approximation (PWL) combined with fixed-point optimization. Their technique divides the sigmoid function into multiple segments with different slopes, implementing a lookup table-based approach that significantly reduces computational complexity. The implementation uses fixed-point arithmetic with careful bit-width optimization to balance accuracy and resource utilization. Their method achieves an average approximation error of less than 0.1% while reducing computation time by approximately 70% compared to floating-point implementations. The university has also developed specialized hardware accelerators that implement these approximation techniques directly in silicon, further enhancing performance for edge AI applications. Their research demonstrates that carefully designed PWL approximations can achieve near-identical neural network accuracy compared to full precision sigmoid implementations[1][3].
Strengths: Achieves excellent balance between accuracy and computational efficiency; implementation is highly optimized for resource-constrained microcontrollers; provides comprehensive error analysis across different bit-width configurations. Weaknesses: The piecewise approach requires conditional branching which may impact performance on some microcontroller architectures; lookup table requirements may limit applicability on extremely memory-constrained devices.
Key Innovations in Fixed-point Neural Network Inference
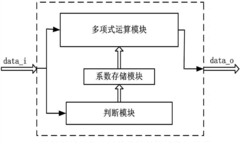
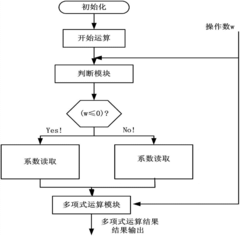
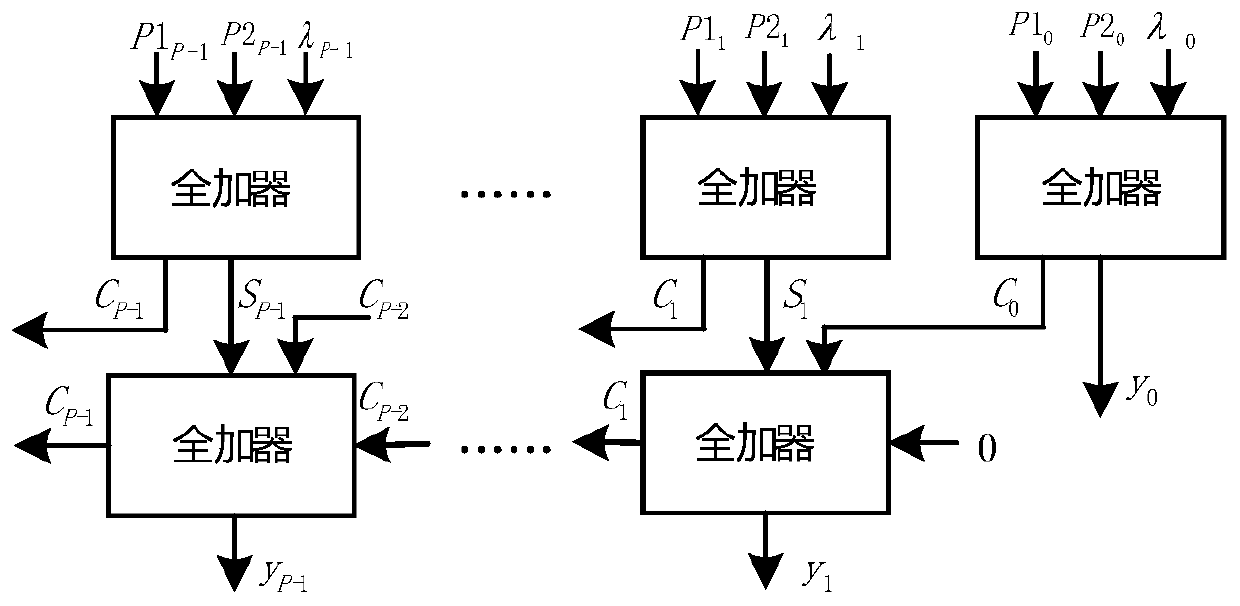
Sigmoid function fitting hardware circuit based on Remez approximating algorithm
PatentActiveCN107247992A
Innovation
- The sigmoid function based on the Lemez approximation algorithm is used to fit the hardware circuit. By determining the order and interval division of the fitting polynomial, combined with Chebyshev polynomials and linear equations, high-precision polynomial fitting is achieved, and the float is designed. Point operation module and judgment module optimize data format and storage resource usage.
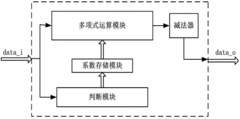
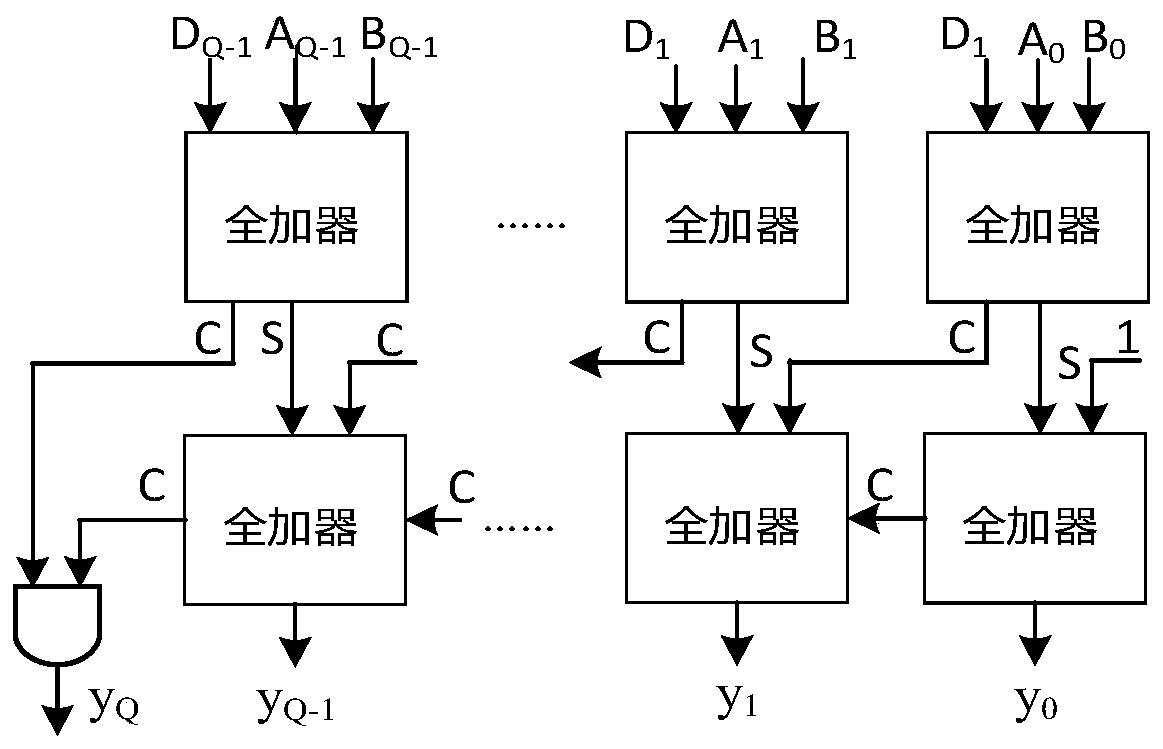
Approximate calculation device for sigmoid function
PatentActiveCN110837624A
Innovation
- An approximate computing device including a negative input conversion unit, a constant multiplication unit, a shift unit, a special value generation unit, a carry-preserving adder and a negative result conversion unit is designed, which replaces multiplication through the rapid generation of special values and shift operations. Reduce latency and area overhead, and use carry-preserving adders to optimize computing latency.
Power Consumption and Performance Trade-offs
The implementation of sigmoid approximation techniques on microcontrollers involves critical trade-offs between power consumption and computational performance. Fixed-point implementations significantly reduce power requirements compared to floating-point operations, with studies showing power savings of 30-70% depending on the specific microcontroller architecture. However, these savings must be balanced against potential accuracy losses and execution time considerations.
Power efficiency varies substantially across different approximation methods. Lookup table approaches consume minimal computational power but require memory resources that may increase overall system power draw, especially when cache misses occur. Piecewise linear approximations strike a middle ground, offering reasonable power efficiency with moderate accuracy. Polynomial approximations typically demand more computational resources, resulting in higher power consumption, though this can be mitigated through coefficient optimization.
The bit-width selection in fixed-point implementations directly impacts both power consumption and performance. Lower bit-widths (8-bit or 16-bit) consume significantly less power but may introduce quantization errors that affect model accuracy. Higher precision implementations (24-bit or 32-bit) provide better accuracy but at the cost of increased power draw and reduced inference speed. Recent research indicates that adaptive bit-width selection based on layer sensitivity can optimize this trade-off.
Clock frequency adjustments represent another critical consideration. Dynamic frequency scaling techniques can reduce power consumption by 40-60% during less computationally intensive portions of inference operations. Some advanced microcontroller platforms now incorporate hardware-accelerated sigmoid approximation units that deliver up to 5x better performance-per-watt compared to software implementations.
Temperature effects must also be considered in the power-performance equation. Higher computational loads from complex approximation methods increase chip temperature, potentially triggering thermal throttling that degrades performance. Simpler approximation methods may maintain more consistent performance across varying environmental conditions, which is particularly important for battery-powered edge devices operating in unpredictable environments.
The memory access patterns of different approximation techniques significantly impact overall system efficiency. Methods requiring frequent, non-sequential memory access can increase power consumption through cache misses and memory controller activity. Techniques that maintain data locality and minimize external memory access generally demonstrate superior power efficiency, even if their computational complexity is somewhat higher.
Power efficiency varies substantially across different approximation methods. Lookup table approaches consume minimal computational power but require memory resources that may increase overall system power draw, especially when cache misses occur. Piecewise linear approximations strike a middle ground, offering reasonable power efficiency with moderate accuracy. Polynomial approximations typically demand more computational resources, resulting in higher power consumption, though this can be mitigated through coefficient optimization.
The bit-width selection in fixed-point implementations directly impacts both power consumption and performance. Lower bit-widths (8-bit or 16-bit) consume significantly less power but may introduce quantization errors that affect model accuracy. Higher precision implementations (24-bit or 32-bit) provide better accuracy but at the cost of increased power draw and reduced inference speed. Recent research indicates that adaptive bit-width selection based on layer sensitivity can optimize this trade-off.
Clock frequency adjustments represent another critical consideration. Dynamic frequency scaling techniques can reduce power consumption by 40-60% during less computationally intensive portions of inference operations. Some advanced microcontroller platforms now incorporate hardware-accelerated sigmoid approximation units that deliver up to 5x better performance-per-watt compared to software implementations.
Temperature effects must also be considered in the power-performance equation. Higher computational loads from complex approximation methods increase chip temperature, potentially triggering thermal throttling that degrades performance. Simpler approximation methods may maintain more consistent performance across varying environmental conditions, which is particularly important for battery-powered edge devices operating in unpredictable environments.
The memory access patterns of different approximation techniques significantly impact overall system efficiency. Methods requiring frequent, non-sequential memory access can increase power consumption through cache misses and memory controller activity. Techniques that maintain data locality and minimize external memory access generally demonstrate superior power efficiency, even if their computational complexity is somewhat higher.
Hardware-specific Optimization Strategies
Microcontroller architectures vary significantly in their computational capabilities, memory constraints, and instruction sets, necessitating tailored optimization strategies for sigmoid approximation. ARM Cortex-M series, widely used in embedded applications, offers specific SIMD (Single Instruction, Multiple Data) instructions that can accelerate fixed-point operations when properly leveraged. For these processors, bit-shifting operations are particularly efficient and should be prioritized over division operations whenever possible in sigmoid approximations.
Memory alignment considerations play a crucial role in optimization. Ensuring that fixed-point data structures are aligned to the natural word boundaries of the target microcontroller can significantly reduce access latencies. For 32-bit architectures, aligning data to 4-byte boundaries can improve performance by up to 30% in sigmoid computation routines.
Instruction pipelining characteristics of different microcontrollers must be considered when implementing sigmoid approximations. For instance, on architectures with deep pipelines, reducing branch instructions through techniques like loop unrolling can prevent pipeline stalls. The Texas Instruments MSP430 series, with its limited pipeline depth, benefits more from code size reduction than branch elimination strategies.
Cache utilization strategies differ across microcontroller families. For devices with instruction and data caches, organizing sigmoid computation code to maximize cache locality can yield substantial performance improvements. This includes arranging weight matrices and activation functions in memory to minimize cache misses during inference operations.
Power consumption profiles should guide optimization choices, especially for battery-powered applications. Some microcontrollers offer low-power modes that can be strategically engaged between computation blocks. Fixed-point sigmoid implementations can be designed to leverage these modes by batching computations efficiently.
Hardware accelerators present in modern microcontrollers can be exploited for sigmoid approximation. Many STM32 series microcontrollers include digital signal processing (DSP) extensions that enable single-cycle multiply-accumulate operations, which are ideal for polynomial approximations of sigmoid functions. Similarly, ESP32's floating-point unit can be leveraged for hybrid fixed-floating point approaches when higher precision is required at specific ranges of the sigmoid curve.
Register allocation strategies should be customized based on the register file size of the target architecture. RISC-V implementations typically offer more general-purpose registers than 8-bit microcontrollers, allowing more intermediate values to be kept in registers during sigmoid computation, reducing memory access overhead.
Memory alignment considerations play a crucial role in optimization. Ensuring that fixed-point data structures are aligned to the natural word boundaries of the target microcontroller can significantly reduce access latencies. For 32-bit architectures, aligning data to 4-byte boundaries can improve performance by up to 30% in sigmoid computation routines.
Instruction pipelining characteristics of different microcontrollers must be considered when implementing sigmoid approximations. For instance, on architectures with deep pipelines, reducing branch instructions through techniques like loop unrolling can prevent pipeline stalls. The Texas Instruments MSP430 series, with its limited pipeline depth, benefits more from code size reduction than branch elimination strategies.
Cache utilization strategies differ across microcontroller families. For devices with instruction and data caches, organizing sigmoid computation code to maximize cache locality can yield substantial performance improvements. This includes arranging weight matrices and activation functions in memory to minimize cache misses during inference operations.
Power consumption profiles should guide optimization choices, especially for battery-powered applications. Some microcontrollers offer low-power modes that can be strategically engaged between computation blocks. Fixed-point sigmoid implementations can be designed to leverage these modes by batching computations efficiently.
Hardware accelerators present in modern microcontrollers can be exploited for sigmoid approximation. Many STM32 series microcontrollers include digital signal processing (DSP) extensions that enable single-cycle multiply-accumulate operations, which are ideal for polynomial approximations of sigmoid functions. Similarly, ESP32's floating-point unit can be leveraged for hybrid fixed-floating point approaches when higher precision is required at specific ranges of the sigmoid curve.
Register allocation strategies should be customized based on the register file size of the target architecture. RISC-V implementations typically offer more general-purpose registers than 8-bit microcontrollers, allowing more intermediate values to be kept in registers during sigmoid computation, reducing memory access overhead.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!