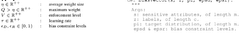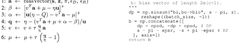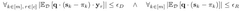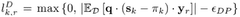Optimization Tricks When Training Sigmoid-based Networks on Imbalanced Data — Techniques & Benchmarks
AUG 21, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Sigmoid Networks Optimization Background and Objectives
Neural networks utilizing sigmoid activation functions have been a cornerstone of machine learning since the early days of artificial intelligence research. The sigmoid function, characterized by its S-shaped curve that maps any input to a value between 0 and 1, has historically been the activation function of choice for binary classification problems. However, when faced with imbalanced datasets—where one class significantly outnumbers the other—these networks often exhibit suboptimal performance due to inherent biases toward the majority class.
The evolution of sigmoid-based networks can be traced back to the perceptron model introduced in the late 1950s, which later evolved into multi-layer perceptrons (MLPs) with the advent of backpropagation in the 1980s. Despite the emergence of alternative activation functions like ReLU and its variants in recent years, sigmoid functions remain relevant for specific applications, particularly in binary classification tasks and as output activations in various network architectures.
Imbalanced data presents a persistent challenge across numerous domains, including fraud detection, medical diagnosis, and anomaly detection. In these scenarios, the minority class often represents the events of interest, making accurate classification crucial despite their rarity. Traditional training approaches tend to produce models that favor the majority class, resulting in high overall accuracy but poor performance on the critical minority class.
Recent research has focused on developing specialized optimization techniques to address these challenges. These include algorithmic approaches such as cost-sensitive learning, resampling methods, and advanced loss function modifications. Additionally, architectural innovations and training regime adaptations have shown promise in improving performance on imbalanced datasets.
The primary objective of this technical research is to comprehensively evaluate and benchmark various optimization techniques specifically designed for sigmoid-based networks when trained on imbalanced data. We aim to identify the most effective approaches across different imbalance ratios and application domains, providing practical guidelines for practitioners facing similar challenges.
Furthermore, this research seeks to explore the theoretical underpinnings of why certain optimization tricks prove effective, examining the gradient dynamics, convergence properties, and representation learning aspects of sigmoid networks under imbalanced conditions. By understanding these mechanisms, we hope to inspire novel approaches that can further advance the state of the art in this critical area of machine learning.
The evolution of sigmoid-based networks can be traced back to the perceptron model introduced in the late 1950s, which later evolved into multi-layer perceptrons (MLPs) with the advent of backpropagation in the 1980s. Despite the emergence of alternative activation functions like ReLU and its variants in recent years, sigmoid functions remain relevant for specific applications, particularly in binary classification tasks and as output activations in various network architectures.
Imbalanced data presents a persistent challenge across numerous domains, including fraud detection, medical diagnosis, and anomaly detection. In these scenarios, the minority class often represents the events of interest, making accurate classification crucial despite their rarity. Traditional training approaches tend to produce models that favor the majority class, resulting in high overall accuracy but poor performance on the critical minority class.
Recent research has focused on developing specialized optimization techniques to address these challenges. These include algorithmic approaches such as cost-sensitive learning, resampling methods, and advanced loss function modifications. Additionally, architectural innovations and training regime adaptations have shown promise in improving performance on imbalanced datasets.
The primary objective of this technical research is to comprehensively evaluate and benchmark various optimization techniques specifically designed for sigmoid-based networks when trained on imbalanced data. We aim to identify the most effective approaches across different imbalance ratios and application domains, providing practical guidelines for practitioners facing similar challenges.
Furthermore, this research seeks to explore the theoretical underpinnings of why certain optimization tricks prove effective, examining the gradient dynamics, convergence properties, and representation learning aspects of sigmoid networks under imbalanced conditions. By understanding these mechanisms, we hope to inspire novel approaches that can further advance the state of the art in this critical area of machine learning.
Market Demand Analysis for Imbalanced Data Solutions
The market for solutions addressing imbalanced data in machine learning has experienced significant growth in recent years, driven by the increasing adoption of AI across various industries. Organizations dealing with fraud detection, medical diagnostics, predictive maintenance, and rare event prediction face persistent challenges with class imbalance, creating substantial demand for specialized optimization techniques for sigmoid-based networks.
Financial services represent one of the largest market segments, with fraud detection systems requiring robust handling of highly imbalanced datasets where fraudulent transactions typically constitute less than 1% of all transactions. According to industry reports, the fraud detection market is expected to reach $65 billion by 2026, with imbalanced data solutions being a critical component of this ecosystem.
Healthcare presents another substantial market opportunity, particularly in disease diagnosis where rare conditions create natural data imbalances. The medical AI diagnostics market is growing at 40% annually, with imbalanced data handling capabilities becoming a key differentiator for solution providers. Pharmaceutical companies also require these solutions for drug discovery processes where positive outcomes are rare among tested compounds.
Manufacturing and industrial IoT applications demonstrate increasing demand for predictive maintenance solutions that can effectively identify rare equipment failure patterns. The predictive maintenance market is projected to reach $23 billion by 2024, with imbalanced data handling being essential to accurate failure prediction models.
The cybersecurity sector represents another significant market, with intrusion detection systems needing to identify rare attack patterns among normal network traffic. This market segment is growing at 15% annually, with specialized solutions for imbalanced data commanding premium pricing.
Market research indicates that organizations are willing to pay 30-40% more for machine learning solutions that demonstrate superior performance on imbalanced datasets compared to standard approaches. This price premium reflects the business value of reducing false negatives in critical applications.
The competitive landscape shows increasing specialization, with both established AI platform providers and startups developing dedicated tools for imbalanced data scenarios. Cloud service providers have begun offering specialized services targeting this market need, indicating its growing importance in the broader AI ecosystem.
Financial services represent one of the largest market segments, with fraud detection systems requiring robust handling of highly imbalanced datasets where fraudulent transactions typically constitute less than 1% of all transactions. According to industry reports, the fraud detection market is expected to reach $65 billion by 2026, with imbalanced data solutions being a critical component of this ecosystem.
Healthcare presents another substantial market opportunity, particularly in disease diagnosis where rare conditions create natural data imbalances. The medical AI diagnostics market is growing at 40% annually, with imbalanced data handling capabilities becoming a key differentiator for solution providers. Pharmaceutical companies also require these solutions for drug discovery processes where positive outcomes are rare among tested compounds.
Manufacturing and industrial IoT applications demonstrate increasing demand for predictive maintenance solutions that can effectively identify rare equipment failure patterns. The predictive maintenance market is projected to reach $23 billion by 2024, with imbalanced data handling being essential to accurate failure prediction models.
The cybersecurity sector represents another significant market, with intrusion detection systems needing to identify rare attack patterns among normal network traffic. This market segment is growing at 15% annually, with specialized solutions for imbalanced data commanding premium pricing.
Market research indicates that organizations are willing to pay 30-40% more for machine learning solutions that demonstrate superior performance on imbalanced datasets compared to standard approaches. This price premium reflects the business value of reducing false negatives in critical applications.
The competitive landscape shows increasing specialization, with both established AI platform providers and startups developing dedicated tools for imbalanced data scenarios. Cloud service providers have begun offering specialized services targeting this market need, indicating its growing importance in the broader AI ecosystem.
Current Challenges in Sigmoid-based Network Training
Despite significant advancements in neural network architectures, sigmoid-based networks continue to face substantial challenges when dealing with imbalanced datasets. The sigmoid activation function, while theoretically elegant for binary classification problems, exhibits problematic behavior in practice when class distributions are skewed. The vanishing gradient problem becomes particularly pronounced in these scenarios, as the sigmoid function saturates quickly at extreme values, causing gradients to approach zero and significantly slowing down the learning process for the minority class.
Class imbalance exacerbates this issue by creating a statistical bias toward the majority class. Networks tend to optimize for overall accuracy by predicting the dominant class, resulting in models that appear statistically successful but fail to identify the often more important minority class instances. This phenomenon is especially problematic in critical domains like medical diagnostics, fraud detection, and anomaly identification where the rare events are typically of greatest interest.
Traditional loss functions such as binary cross-entropy are inadequate for imbalanced data scenarios as they treat all misclassifications equally. When one class significantly outnumbers another, the cumulative loss from the majority class dominates the optimization process, leading the model to prioritize majority class performance at the expense of minority class detection.
Batch composition presents another significant challenge. Standard random batch sampling tends to reflect the original data distribution, potentially creating batches with few or no minority class examples. This sampling imbalance creates inconsistent gradient updates and unstable training dynamics, particularly for deep networks where gradient propagation is already challenging.
Hyperparameter optimization becomes exceptionally difficult in imbalanced scenarios. Learning rates that work well for balanced datasets often prove problematic when classes are skewed, as they may be too aggressive for the sparse updates related to minority classes or too conservative for effective majority class learning. Similarly, weight initialization schemes designed for balanced data distributions can create unfavorable starting conditions for imbalanced learning tasks.
Feature representation issues compound these challenges. In many imbalanced datasets, the minority class occupies a small, potentially fragmented region of the feature space. Sigmoid-based networks struggle to establish appropriate decision boundaries in such scenarios, particularly when minority class instances exhibit high variance or exist as small clusters within majority-dominated regions.
Evaluation metrics present a final critical challenge. Accuracy, the most commonly used metric, becomes misleading with imbalanced data. A model achieving 99% accuracy on a dataset with a 99:1 class ratio may simply be predicting the majority class exclusively, providing no actual discriminative value. This necessitates specialized evaluation frameworks that can properly assess model performance on imbalanced data.
Class imbalance exacerbates this issue by creating a statistical bias toward the majority class. Networks tend to optimize for overall accuracy by predicting the dominant class, resulting in models that appear statistically successful but fail to identify the often more important minority class instances. This phenomenon is especially problematic in critical domains like medical diagnostics, fraud detection, and anomaly identification where the rare events are typically of greatest interest.
Traditional loss functions such as binary cross-entropy are inadequate for imbalanced data scenarios as they treat all misclassifications equally. When one class significantly outnumbers another, the cumulative loss from the majority class dominates the optimization process, leading the model to prioritize majority class performance at the expense of minority class detection.
Batch composition presents another significant challenge. Standard random batch sampling tends to reflect the original data distribution, potentially creating batches with few or no minority class examples. This sampling imbalance creates inconsistent gradient updates and unstable training dynamics, particularly for deep networks where gradient propagation is already challenging.
Hyperparameter optimization becomes exceptionally difficult in imbalanced scenarios. Learning rates that work well for balanced datasets often prove problematic when classes are skewed, as they may be too aggressive for the sparse updates related to minority classes or too conservative for effective majority class learning. Similarly, weight initialization schemes designed for balanced data distributions can create unfavorable starting conditions for imbalanced learning tasks.
Feature representation issues compound these challenges. In many imbalanced datasets, the minority class occupies a small, potentially fragmented region of the feature space. Sigmoid-based networks struggle to establish appropriate decision boundaries in such scenarios, particularly when minority class instances exhibit high variance or exist as small clusters within majority-dominated regions.
Evaluation metrics present a final critical challenge. Accuracy, the most commonly used metric, becomes misleading with imbalanced data. A model achieving 99% accuracy on a dataset with a 99:1 class ratio may simply be predicting the majority class exclusively, providing no actual discriminative value. This necessitates specialized evaluation frameworks that can properly assess model performance on imbalanced data.
Existing Optimization Tricks for Sigmoid-based Networks
01 Optimization techniques for sigmoid activation functions in neural networks
Various optimization techniques can be applied to sigmoid-based neural networks to improve performance and convergence. These include gradient-based methods, adaptive learning rates, and specialized algorithms designed to overcome the vanishing gradient problem inherent in sigmoid functions. By implementing these optimization strategies, neural networks with sigmoid activation functions can achieve better accuracy and faster training times.- Optimization algorithms for sigmoid neural networks: Various optimization algorithms are employed to enhance the performance of sigmoid-based neural networks. These algorithms focus on improving convergence speed, reducing computational complexity, and enhancing accuracy. Techniques include gradient descent variants, adaptive learning rate methods, and specialized optimization approaches designed specifically for sigmoid activation functions to overcome issues like vanishing gradients.
- Hardware implementations of sigmoid functions: Hardware-specific optimizations for sigmoid functions in neural networks involve specialized circuit designs and architectures. These implementations aim to reduce power consumption, increase processing speed, and improve efficiency in FPGA, ASIC, or other hardware platforms. Custom hardware solutions can significantly accelerate sigmoid computations compared to software implementations while maintaining numerical precision.
- Approximation methods for sigmoid functions: Various approximation techniques are used to simplify sigmoid function computations while maintaining acceptable accuracy. These methods include piecewise linear approximations, lookup tables, polynomial approximations, and other mathematical simplifications that reduce computational complexity. Such approximations enable faster network training and inference while preserving the essential characteristics of the sigmoid activation function.
- Sigmoid-based networks in wireless communications: Sigmoid neural networks are applied to wireless communication systems for signal processing, channel estimation, and network optimization. These networks help improve signal quality, reduce interference, optimize resource allocation, and enhance overall network performance. The adaptability of sigmoid functions makes them particularly suitable for modeling complex wireless channel behaviors and optimizing transmission parameters.
- Deep learning architectures with sigmoid activation: Advanced deep learning architectures incorporate sigmoid activation functions in specific network layers for particular tasks. These architectures may combine sigmoid with other activation functions to leverage their complementary properties. Optimization techniques specific to deep sigmoid networks include specialized initialization methods, normalization techniques, and training strategies that address the limitations of sigmoid functions in deep networks.
02 Hardware implementations of sigmoid function optimizations
Hardware-specific optimizations for sigmoid functions focus on efficient circuit designs and specialized architectures that reduce computational complexity and power consumption. These implementations may use approximation methods, lookup tables, or dedicated processing units to accelerate sigmoid calculations in neural network applications. Such hardware optimizations are particularly important for edge devices and real-time applications where processing resources are limited.Expand Specific Solutions03 Sigmoid-based network optimization for wireless communications
In wireless communication systems, sigmoid-based networks are optimized for signal processing, channel estimation, and resource allocation. These optimizations involve specialized training algorithms and network architectures designed to handle the unique challenges of wireless environments, such as signal fading and interference. By optimizing sigmoid-based networks for these applications, improved communication reliability and efficiency can be achieved.Expand Specific Solutions04 Deep learning optimizations for sigmoid neural networks
Deep learning frameworks incorporate specific optimizations for sigmoid activation functions in multi-layer networks. These include initialization strategies, normalization techniques, and architectural modifications that address the limitations of sigmoid functions in deep networks. Advanced regularization methods and training procedures help mitigate issues like saturation and slow convergence, enabling more effective training of deep sigmoid-based networks.Expand Specific Solutions05 Approximation methods for sigmoid function computation
Various mathematical approximation techniques can be used to optimize the computation of sigmoid functions in neural networks. These include piecewise linear approximations, polynomial approximations, and lookup table-based methods that reduce computational complexity while maintaining acceptable accuracy. Such approximation methods are particularly valuable for resource-constrained environments where the exact computation of sigmoid functions would be prohibitively expensive.Expand Specific Solutions
Leading Organizations and Researchers in Neural Network Optimization
The sigmoid-based network optimization for imbalanced data landscape is currently in a growth phase, with the market expanding as AI applications proliferate across industries. The technology is approaching maturity with significant contributions from major players like Google, Microsoft, and IBM, who are developing enterprise-scale solutions. DeepMind and Baidu are advancing theoretical frameworks, while specialized firms like Akridata and Sualab focus on industrial applications. Academic institutions including Southeast University and Tianjin Normal University contribute fundamental research. The technology shows particular promise in financial services, with Royal Bank of Canada and Capital One implementing these techniques for fraud detection and risk assessment. The competitive landscape reflects a balance between established tech giants and specialized AI firms developing domain-specific implementations.
International Business Machines Corp.
Technical Solution: IBM has developed a robust enterprise solution for training sigmoid-based networks on imbalanced data through their Watson Machine Learning platform. Their approach combines traditional techniques with novel innovations specifically designed for business applications. IBM's solution implements a hierarchical sampling strategy that creates balanced mini-batches while preserving important majority class examples identified through their proprietary "Information Gain Filtering" algorithm. They've developed specialized sigmoid activation functions with learnable parameters that adapt to class distributions during training. IBM's technique incorporates a "Progressive Margin Enhancement" loss function that dynamically adjusts classification margins based on class frequencies and sample difficulties. Their implementation includes automated hyperparameter optimization specifically tuned for imbalanced data scenarios, which systematically explores learning rate schedules, batch sizes, and regularization strengths optimal for different imbalance ratios. IBM's solution also features interpretability tools that help explain model decisions even when trained on highly skewed datasets.
Strengths: Enterprise-ready implementation with strong security and governance features; excellent scalability for large industrial datasets; comprehensive support for regulatory compliance scenarios. Weaknesses: Higher implementation complexity compared to open-source alternatives; some advanced features require significant computational resources.
Google LLC
Technical Solution: Google's approach to sigmoid-based networks on imbalanced data leverages their TensorFlow framework with specialized optimization techniques. Their solution implements focal loss modifications that dynamically adjust the loss contribution of well-classified examples, reducing their impact during training. Google has developed adaptive learning rate schedulers specifically designed for imbalanced datasets, which automatically adjust learning rates based on class distribution metrics. Their technique incorporates gradient centralization and normalization methods that stabilize training by preventing gradient explosion in minority classes. Additionally, Google employs a two-phase training strategy where the model first learns general patterns from all data before fine-tuning on minority classes with adjusted class weights. Their implementation includes specialized regularization techniques that prevent overfitting to majority classes while maintaining model generalization capabilities across all classes.
Strengths: Seamless integration with TensorFlow ecosystem; highly scalable implementation suitable for large-scale deployments; extensive hyperparameter tuning capabilities. Weaknesses: Requires significant computational resources for optimal performance; complex implementation may require specialized expertise to fully leverage all optimization techniques.
Key Technical Innovations in Imbalanced Data Training
Balancing training data for training neural networks
PatentWO2025068441A1
Innovation
- The technique involves determining item attribute vectors for each training item to assess the likelihood of exhibiting specific attributes, defining weight values for each item, and iteratively minimizing a loss function to rebalance the training database, thereby reducing association bias.
Benchmarking Methodologies and Performance Metrics
To effectively evaluate optimization techniques for sigmoid-based networks on imbalanced data, robust benchmarking methodologies and standardized performance metrics are essential. These provide the foundation for meaningful comparisons across different approaches and ensure reproducibility of results.
Standard benchmarking datasets for imbalanced classification include MNIST-Imbalanced, CIFAR-10-Imbalanced, and real-world datasets such as credit card fraud detection, medical diagnosis, and rare event prediction. These datasets exhibit varying degrees of class imbalance ratios, typically ranging from 1:10 to 1:1000, allowing for comprehensive evaluation across different imbalance scenarios.
Cross-validation techniques specifically adapted for imbalanced data are crucial in the benchmarking process. Stratified k-fold cross-validation ensures that each fold maintains the original class distribution, while specialized techniques like stratified iterative stratification address multi-label imbalanced datasets. These validation approaches help mitigate the risk of overfitting to the majority class.
Performance metrics for imbalanced data extend beyond traditional accuracy, which can be misleading when one class dominates. Precision, recall, and F1-score provide more nuanced evaluation, with F1-score offering a harmonic mean between precision and recall. The Area Under the Receiver Operating Characteristic curve (AUROC) and Area Under the Precision-Recall curve (AUPRC) offer comprehensive assessments of classifier performance across different threshold settings, with AUPRC being particularly sensitive to imbalance.
Matthews Correlation Coefficient (MCC) and Cohen's Kappa are increasingly adopted as they account for all confusion matrix elements and correct for chance agreement, respectively. For severe imbalance scenarios, G-mean (geometric mean of sensitivity and specificity) provides insights into balanced accuracy across classes.
Computational efficiency metrics complement performance evaluation, measuring training time, inference speed, and memory requirements across different optimization techniques. These practical considerations are particularly relevant for resource-constrained environments and real-time applications.
Benchmark protocols should include multiple random initializations to account for variance in neural network training, with statistical significance testing (e.g., paired t-tests or Wilcoxon signed-rank tests) to validate performance differences between methods. Ablation studies isolate the contribution of individual optimization components, providing deeper insights into which techniques offer the most substantial improvements for sigmoid-based networks on imbalanced data.
Standard benchmarking datasets for imbalanced classification include MNIST-Imbalanced, CIFAR-10-Imbalanced, and real-world datasets such as credit card fraud detection, medical diagnosis, and rare event prediction. These datasets exhibit varying degrees of class imbalance ratios, typically ranging from 1:10 to 1:1000, allowing for comprehensive evaluation across different imbalance scenarios.
Cross-validation techniques specifically adapted for imbalanced data are crucial in the benchmarking process. Stratified k-fold cross-validation ensures that each fold maintains the original class distribution, while specialized techniques like stratified iterative stratification address multi-label imbalanced datasets. These validation approaches help mitigate the risk of overfitting to the majority class.
Performance metrics for imbalanced data extend beyond traditional accuracy, which can be misleading when one class dominates. Precision, recall, and F1-score provide more nuanced evaluation, with F1-score offering a harmonic mean between precision and recall. The Area Under the Receiver Operating Characteristic curve (AUROC) and Area Under the Precision-Recall curve (AUPRC) offer comprehensive assessments of classifier performance across different threshold settings, with AUPRC being particularly sensitive to imbalance.
Matthews Correlation Coefficient (MCC) and Cohen's Kappa are increasingly adopted as they account for all confusion matrix elements and correct for chance agreement, respectively. For severe imbalance scenarios, G-mean (geometric mean of sensitivity and specificity) provides insights into balanced accuracy across classes.
Computational efficiency metrics complement performance evaluation, measuring training time, inference speed, and memory requirements across different optimization techniques. These practical considerations are particularly relevant for resource-constrained environments and real-time applications.
Benchmark protocols should include multiple random initializations to account for variance in neural network training, with statistical significance testing (e.g., paired t-tests or Wilcoxon signed-rank tests) to validate performance differences between methods. Ablation studies isolate the contribution of individual optimization components, providing deeper insights into which techniques offer the most substantial improvements for sigmoid-based networks on imbalanced data.
Implementation Strategies and Practical Guidelines
Implementing effective strategies for sigmoid-based networks on imbalanced datasets requires careful consideration of both algorithmic and practical aspects. The choice of optimization techniques should be tailored to the specific characteristics of the dataset and the network architecture.
When initializing sigmoid-based networks for imbalanced data, weight initialization becomes particularly critical. Standard initialization methods like Xavier or He initialization may need modification to account for class imbalance. Adjusting initial weights to be inversely proportional to class frequencies can provide a better starting point for convergence.
Batch construction represents another crucial implementation consideration. Rather than using random sampling, implementing class-aware sampling strategies ensures each mini-batch contains a representative distribution of classes. Techniques such as stratified sampling maintain class proportions, while oversampling minority classes within batches can improve model sensitivity without requiring preprocessing of the entire dataset.
Learning rate scheduling should be adapted for imbalanced data scenarios. A cyclical learning rate policy with smaller cycles for minority classes can help escape local minima that might otherwise trap the model in majority-class-favoring solutions. Empirical evidence suggests that warm-up periods followed by cosine annealing schedules perform particularly well when dealing with severe imbalances.
Gradient accumulation techniques offer practical benefits when hardware constraints limit batch sizes. By accumulating gradients across multiple forward-backward passes before updating weights, larger effective batch sizes can be achieved without increasing memory requirements. This approach helps stabilize training, especially important when working with imbalanced datasets where individual updates from minority classes might otherwise be overwhelmed.
Early stopping criteria should be carefully selected based on metrics relevant to minority class performance rather than overall accuracy. Implementing patience mechanisms that monitor F1-score or balanced accuracy prevents premature convergence to suboptimal solutions that favor majority classes.
Model checkpointing strategies should preserve models based on minority class performance metrics rather than overall loss. Maintaining an ensemble of checkpoints from different training stages can also provide robustness through model averaging, which often yields better generalization on imbalanced data.
Hyperparameter optimization frameworks should incorporate stratified cross-validation to ensure validation sets maintain the same class distribution challenges as the training data. Bayesian optimization approaches have demonstrated superior performance compared to grid or random search when tuning networks for imbalanced data problems, particularly when optimizing for metrics like AUROC or balanced accuracy.
When initializing sigmoid-based networks for imbalanced data, weight initialization becomes particularly critical. Standard initialization methods like Xavier or He initialization may need modification to account for class imbalance. Adjusting initial weights to be inversely proportional to class frequencies can provide a better starting point for convergence.
Batch construction represents another crucial implementation consideration. Rather than using random sampling, implementing class-aware sampling strategies ensures each mini-batch contains a representative distribution of classes. Techniques such as stratified sampling maintain class proportions, while oversampling minority classes within batches can improve model sensitivity without requiring preprocessing of the entire dataset.
Learning rate scheduling should be adapted for imbalanced data scenarios. A cyclical learning rate policy with smaller cycles for minority classes can help escape local minima that might otherwise trap the model in majority-class-favoring solutions. Empirical evidence suggests that warm-up periods followed by cosine annealing schedules perform particularly well when dealing with severe imbalances.
Gradient accumulation techniques offer practical benefits when hardware constraints limit batch sizes. By accumulating gradients across multiple forward-backward passes before updating weights, larger effective batch sizes can be achieved without increasing memory requirements. This approach helps stabilize training, especially important when working with imbalanced datasets where individual updates from minority classes might otherwise be overwhelmed.
Early stopping criteria should be carefully selected based on metrics relevant to minority class performance rather than overall accuracy. Implementing patience mechanisms that monitor F1-score or balanced accuracy prevents premature convergence to suboptimal solutions that favor majority classes.
Model checkpointing strategies should preserve models based on minority class performance metrics rather than overall loss. Maintaining an ensemble of checkpoints from different training stages can also provide robustness through model averaging, which often yields better generalization on imbalanced data.
Hyperparameter optimization frameworks should incorporate stratified cross-validation to ensure validation sets maintain the same class distribution challenges as the training data. Bayesian optimization approaches have demonstrated superior performance compared to grid or random search when tuning networks for imbalanced data problems, particularly when optimizing for metrics like AUROC or balanced accuracy.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!