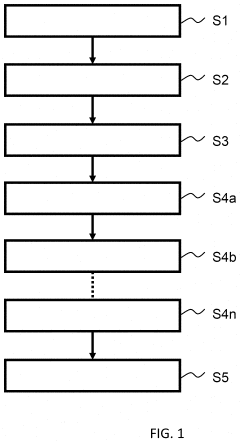
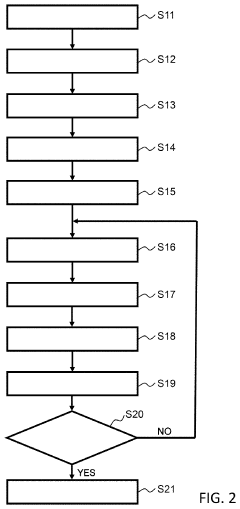
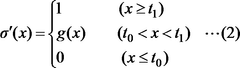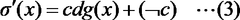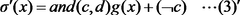Sigmoid Function and Probability Calibration: Platt Scaling, Temperature Scaling and Use Cases
AUG 21, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Sigmoid Function Evolution and Calibration Objectives
The sigmoid function, originating from mathematical biology in the 19th century, has evolved significantly from its initial application in population growth models to becoming a cornerstone in modern machine learning. Initially formalized by Pierre François Verhulst in 1838 as the logistic function, it was designed to model population growth with limited resources. This S-shaped curve, characterized by its ability to map any real-valued number to a value between 0 and 1, has proven invaluable across numerous technological domains.
In the context of machine learning, the sigmoid function emerged as a critical activation function in neural networks during the 1980s and 1990s. Its differentiable nature made it particularly suitable for backpropagation algorithms, enabling efficient training of multi-layer networks. The function's ability to transform linear combinations of inputs into probability-like outputs established it as the default choice for binary classification problems.
However, as machine learning applications expanded, researchers identified a significant limitation: raw outputs from sigmoid functions often do not represent well-calibrated probabilities. This recognition led to the development of probability calibration techniques, with John Platt's work in 1999 introducing what became known as Platt Scaling, a post-processing method specifically designed to transform SVM outputs into calibrated probabilities.
The evolution continued with Temperature Scaling, introduced by Guo et al. in 2017, which addressed calibration issues in modern neural networks. This simpler yet effective approach applies a single parameter to adjust the "temperature" of softmax outputs, proving particularly valuable for deep learning models that tend to produce overconfident predictions.
The technical objectives of calibration have expanded beyond merely improving probability estimates. Modern calibration techniques aim to enhance model reliability in critical decision-making scenarios, enable meaningful uncertainty quantification, facilitate fair comparison between different models, and support responsible deployment of AI systems where understanding prediction confidence is essential.
Recent research has focused on developing calibration methods that maintain performance across distribution shifts, operate efficiently at scale, and provide theoretical guarantees. The integration of calibration techniques with Bayesian methods and ensemble approaches represents the cutting edge of this field, aiming to deliver robust uncertainty estimates alongside predictions.
As AI systems increasingly influence high-stakes decisions in healthcare, autonomous vehicles, and financial services, the evolution of sigmoid functions and calibration methods continues toward creating trustworthy systems that not only make accurate predictions but also reliably communicate their confidence levels.
In the context of machine learning, the sigmoid function emerged as a critical activation function in neural networks during the 1980s and 1990s. Its differentiable nature made it particularly suitable for backpropagation algorithms, enabling efficient training of multi-layer networks. The function's ability to transform linear combinations of inputs into probability-like outputs established it as the default choice for binary classification problems.
However, as machine learning applications expanded, researchers identified a significant limitation: raw outputs from sigmoid functions often do not represent well-calibrated probabilities. This recognition led to the development of probability calibration techniques, with John Platt's work in 1999 introducing what became known as Platt Scaling, a post-processing method specifically designed to transform SVM outputs into calibrated probabilities.
The evolution continued with Temperature Scaling, introduced by Guo et al. in 2017, which addressed calibration issues in modern neural networks. This simpler yet effective approach applies a single parameter to adjust the "temperature" of softmax outputs, proving particularly valuable for deep learning models that tend to produce overconfident predictions.
The technical objectives of calibration have expanded beyond merely improving probability estimates. Modern calibration techniques aim to enhance model reliability in critical decision-making scenarios, enable meaningful uncertainty quantification, facilitate fair comparison between different models, and support responsible deployment of AI systems where understanding prediction confidence is essential.
Recent research has focused on developing calibration methods that maintain performance across distribution shifts, operate efficiently at scale, and provide theoretical guarantees. The integration of calibration techniques with Bayesian methods and ensemble approaches represents the cutting edge of this field, aiming to deliver robust uncertainty estimates alongside predictions.
As AI systems increasingly influence high-stakes decisions in healthcare, autonomous vehicles, and financial services, the evolution of sigmoid functions and calibration methods continues toward creating trustworthy systems that not only make accurate predictions but also reliably communicate their confidence levels.
Market Applications for Probability Calibration Methods
Probability calibration methods have found significant market applications across various industries where accurate probability estimates are crucial for decision-making processes. In the financial sector, properly calibrated probabilities enable more reliable risk assessment models for credit scoring, fraud detection, and investment portfolio optimization. Financial institutions leverage Platt Scaling to transform raw model outputs into well-calibrated probabilities that directly correspond to default risks, improving loan approval processes and reducing potential losses.
The healthcare industry has embraced probability calibration techniques to enhance diagnostic accuracy and treatment planning. Medical AI systems utilizing Temperature Scaling provide clinicians with reliable confidence scores for disease detection and progression prediction. These calibrated probabilities allow healthcare providers to make more informed decisions about treatment pathways, particularly in critical care scenarios where understanding prediction confidence is essential for patient outcomes.
Insurance companies have implemented calibration methods to refine their actuarial models and pricing strategies. By applying Platt Scaling to their predictive models, insurers can more accurately estimate claim probabilities and set premiums that better reflect actual risk levels. This application has led to more competitive pricing structures while maintaining profitability through improved risk assessment.
In marketing and e-commerce, probability calibration enhances customer behavior prediction models. Recommendation systems and conversion optimization tools benefit from Temperature Scaling by providing more reliable estimates of purchase likelihood, allowing for more effective resource allocation in marketing campaigns and personalized customer experiences that generate higher conversion rates.
Autonomous vehicle systems represent another critical application area, where calibrated probabilities inform decision-making algorithms for navigation and collision avoidance. Well-calibrated confidence scores help self-driving systems determine when to proceed with an action versus when to seek additional information, directly impacting passenger safety and system reliability.
Cybersecurity solutions increasingly incorporate calibrated probabilities for threat detection and response prioritization. Security operations centers use these calibrated scores to triage alerts more effectively, focusing resources on threats with genuinely high probability of being malicious rather than false positives that waste analyst time and organizational resources.
Weather forecasting and climate modeling have also benefited from advances in probability calibration, with meteorological services applying these techniques to provide more accurate precipitation probabilities and extreme weather event predictions, enabling better disaster preparedness and resource planning for both government agencies and private enterprises.
The healthcare industry has embraced probability calibration techniques to enhance diagnostic accuracy and treatment planning. Medical AI systems utilizing Temperature Scaling provide clinicians with reliable confidence scores for disease detection and progression prediction. These calibrated probabilities allow healthcare providers to make more informed decisions about treatment pathways, particularly in critical care scenarios where understanding prediction confidence is essential for patient outcomes.
Insurance companies have implemented calibration methods to refine their actuarial models and pricing strategies. By applying Platt Scaling to their predictive models, insurers can more accurately estimate claim probabilities and set premiums that better reflect actual risk levels. This application has led to more competitive pricing structures while maintaining profitability through improved risk assessment.
In marketing and e-commerce, probability calibration enhances customer behavior prediction models. Recommendation systems and conversion optimization tools benefit from Temperature Scaling by providing more reliable estimates of purchase likelihood, allowing for more effective resource allocation in marketing campaigns and personalized customer experiences that generate higher conversion rates.
Autonomous vehicle systems represent another critical application area, where calibrated probabilities inform decision-making algorithms for navigation and collision avoidance. Well-calibrated confidence scores help self-driving systems determine when to proceed with an action versus when to seek additional information, directly impacting passenger safety and system reliability.
Cybersecurity solutions increasingly incorporate calibrated probabilities for threat detection and response prioritization. Security operations centers use these calibrated scores to triage alerts more effectively, focusing resources on threats with genuinely high probability of being malicious rather than false positives that waste analyst time and organizational resources.
Weather forecasting and climate modeling have also benefited from advances in probability calibration, with meteorological services applying these techniques to provide more accurate precipitation probabilities and extreme weather event predictions, enabling better disaster preparedness and resource planning for both government agencies and private enterprises.
Current Techniques and Limitations in Probability Calibration
Probability calibration is a critical process in machine learning that transforms raw model outputs into well-calibrated probability estimates. Current calibration techniques primarily revolve around post-processing methods applied to trained models. The most prominent approaches include Platt Scaling, Temperature Scaling, Isotonic Regression, and Bayesian Binning into Quantiles (BBQ).
Platt Scaling, introduced by John Platt in 1999, transforms model outputs using a logistic regression model trained on validation data. While effective for binary classification problems, particularly with SVMs, it struggles with modern deep neural networks that produce highly confident but potentially miscalibrated predictions. The method's simplicity makes it widely adopted, but its linear transformation approach limits its effectiveness with complex probability distributions.
Temperature Scaling, a simplified version of Platt Scaling, uses a single parameter (temperature) to soften probability distributions. This technique has gained popularity for calibrating deep neural networks due to its simplicity and effectiveness. However, it applies uniform scaling across all classes, which can be problematic when different classes require different calibration adjustments.
Isotonic Regression offers a non-parametric alternative that learns a piecewise-constant function to map uncalibrated scores to calibrated probabilities. While more flexible than parametric methods, it requires substantial validation data to prevent overfitting and struggles with extrapolation beyond the range of observed scores.
Vector Scaling and Matrix Scaling extend Temperature Scaling by applying class-specific transformations, but they often overfit on validation data, negating their theoretical advantages. Ensemble methods combine multiple calibration techniques but increase computational complexity and model maintenance overhead.
Despite these advances, significant limitations persist. Most calibration methods assume static data distributions, making them vulnerable to distribution shifts in production environments. They also typically operate as post-processing steps, disconnected from the main model training process, which prevents end-to-end optimization. Additionally, calibration for multi-class problems and imbalanced datasets remains challenging, with most techniques developed primarily for binary classification scenarios.
The computational efficiency of calibration methods presents another limitation, particularly for large-scale applications requiring real-time inference. Furthermore, there's a notable lack of standardized evaluation metrics for calibration quality, with researchers using various measures like Expected Calibration Error (ECE), Maximum Calibration Error (MCE), and reliability diagrams, making cross-method comparisons difficult.
Platt Scaling, introduced by John Platt in 1999, transforms model outputs using a logistic regression model trained on validation data. While effective for binary classification problems, particularly with SVMs, it struggles with modern deep neural networks that produce highly confident but potentially miscalibrated predictions. The method's simplicity makes it widely adopted, but its linear transformation approach limits its effectiveness with complex probability distributions.
Temperature Scaling, a simplified version of Platt Scaling, uses a single parameter (temperature) to soften probability distributions. This technique has gained popularity for calibrating deep neural networks due to its simplicity and effectiveness. However, it applies uniform scaling across all classes, which can be problematic when different classes require different calibration adjustments.
Isotonic Regression offers a non-parametric alternative that learns a piecewise-constant function to map uncalibrated scores to calibrated probabilities. While more flexible than parametric methods, it requires substantial validation data to prevent overfitting and struggles with extrapolation beyond the range of observed scores.
Vector Scaling and Matrix Scaling extend Temperature Scaling by applying class-specific transformations, but they often overfit on validation data, negating their theoretical advantages. Ensemble methods combine multiple calibration techniques but increase computational complexity and model maintenance overhead.
Despite these advances, significant limitations persist. Most calibration methods assume static data distributions, making them vulnerable to distribution shifts in production environments. They also typically operate as post-processing steps, disconnected from the main model training process, which prevents end-to-end optimization. Additionally, calibration for multi-class problems and imbalanced datasets remains challenging, with most techniques developed primarily for binary classification scenarios.
The computational efficiency of calibration methods presents another limitation, particularly for large-scale applications requiring real-time inference. Furthermore, there's a notable lack of standardized evaluation metrics for calibration quality, with researchers using various measures like Expected Calibration Error (ECE), Maximum Calibration Error (MCE), and reliability diagrams, making cross-method comparisons difficult.
Implementation Approaches for Platt and Temperature Scaling
01 Sigmoid function for probability calibration in machine learning
Sigmoid functions are widely used in machine learning for probability calibration, converting raw model outputs into well-calibrated probabilities. This approach transforms unbounded scores into the [0,1] range, making them interpretable as probabilities. The sigmoid function's S-shaped curve is particularly effective for binary classification problems, where the output needs to represent the probability of class membership. This calibration technique improves the reliability of probability estimates in various machine learning applications.- Sigmoid function for probability calibration in machine learning: The sigmoid function is widely used in machine learning models to transform raw prediction scores into well-calibrated probabilities. This transformation is essential for classification tasks where probability outputs need to be reliable. The sigmoid function maps any real-valued number to a value between 0 and 1, making it suitable for representing probabilities. This approach helps in improving the accuracy and reliability of prediction models by ensuring that the output probabilities reflect the true likelihood of the predicted events.
- Platt scaling for post-processing model outputs: Platt scaling is a probability calibration technique that applies logistic regression to the outputs of a classification model. It works by fitting a logistic regression model to the classifier's scores, which transforms them into calibrated probabilities. This method is particularly effective for support vector machines and other models that produce uncalibrated scores. Platt scaling helps to ensure that the predicted probabilities accurately reflect the true likelihood of the predicted class, improving the reliability of the model for decision-making applications.
- Temperature scaling for neural network calibration: Temperature scaling is a simple yet effective method for calibrating the output probabilities of neural networks. It works by dividing the logits (pre-softmax activations) by a temperature parameter before applying the softmax function. A higher temperature produces softer probability distributions, while a lower temperature makes them sharper. This single-parameter approach helps to adjust the confidence of neural network predictions without affecting their accuracy. Temperature scaling is particularly useful for deep learning models that tend to be overconfident in their predictions.
- Ensemble methods for improved probability calibration: Ensemble methods combine multiple models to improve the calibration of probability estimates. By aggregating predictions from different models, these methods can reduce variance and provide more reliable probability estimates. Techniques such as bagging, boosting, and stacking can be used to create ensembles that produce well-calibrated probabilities. These approaches are particularly effective when individual models have complementary strengths and weaknesses, allowing the ensemble to achieve better calibration than any single model could provide.
- Evaluation metrics for probability calibration: Various metrics are used to evaluate the quality of probability calibration in machine learning models. These include reliability diagrams, which visually compare predicted probabilities with observed frequencies, and metrics such as Expected Calibration Error (ECE) and Maximum Calibration Error (MCE). Brier score is another common metric that measures the mean squared difference between predicted probabilities and actual outcomes. These evaluation tools help in assessing how well a model's probability estimates align with the true likelihood of events, guiding the selection and refinement of calibration techniques.
02 Platt scaling for post-processing model outputs
Platt scaling is a probability calibration method that applies logistic regression to the outputs of machine learning models. It works by fitting a logistic regression model to the classifier's scores, transforming them into calibrated probabilities. This technique is particularly useful for support vector machines and other models that produce uncalibrated scores. Platt scaling involves learning parameters a and b to transform the output score s into a calibrated probability using the formula P(y=1|s) = 1/(1+exp(as+b)), effectively rescaling the model's confidence estimates.Expand Specific Solutions03 Temperature scaling for neural network calibration
Temperature scaling is a simple yet effective calibration method specifically designed for deep neural networks. It works by dividing the logits (pre-softmax activations) by a temperature parameter T before applying the softmax function. This single-parameter approach preserves the accuracy of the original model while improving probability calibration. Higher temperature values produce softer probability distributions, while lower values make them sharper. Temperature scaling is particularly valuable in applications requiring reliable confidence estimates, such as medical diagnostics or autonomous systems.Expand Specific Solutions04 Calibration evaluation metrics and validation techniques
Various metrics and techniques are used to evaluate the quality of probability calibration in machine learning models. These include reliability diagrams, calibration curves, expected calibration error (ECE), and Brier score. Proper evaluation involves comparing predicted probabilities with actual outcomes across different probability bins. Cross-validation techniques help ensure that calibration methods generalize well to unseen data. These evaluation approaches are essential for verifying that a model's probability outputs accurately reflect the true likelihood of outcomes, particularly in high-stakes applications.Expand Specific Solutions05 Ensemble methods and multi-class calibration approaches
Ensemble methods combine multiple calibration techniques to achieve more robust probability estimates. For multi-class problems, specialized approaches extend binary calibration methods, including one-vs-rest calibration, multinomial scaling, and matrix scaling. These techniques address the unique challenges of calibrating probabilities across multiple classes while maintaining consistency. Ensemble approaches may include weighted combinations of different calibration methods or hierarchical calibration structures. These advanced calibration strategies are particularly important in complex classification scenarios with numerous output classes.Expand Specific Solutions
Leading Organizations and Researchers in Calibration Research
The sigmoid function and probability calibration market is in a growth phase, with increasing applications in machine learning and AI across various industries. The market size is expanding as more companies integrate these techniques for improved model performance. Technologically, the field is maturing with established methods like Platt Scaling and Temperature Scaling becoming standard practices. Leading players include tech giants like Oracle International and Applied Materials, alongside specialized research institutions such as Roche Molecular Systems. Academic institutions like Sichuan University and Beijing Institute of Technology contribute significant research, while semiconductor companies like ASML, NXP, and Tokyo Electron implement these techniques in advanced manufacturing processes. The ecosystem shows a balanced mix of commercial applications and ongoing research development.
Agilent Technologies, Inc.
Technical Solution: Agilent Technologies has implemented sophisticated probability calibration techniques in their analytical instrumentation software, particularly for mass spectrometry and chromatography applications. Their approach combines modified Platt Scaling with domain-specific transformations to convert raw detection scores into well-calibrated probabilities for compound identification and quantification. Agilent's implementation addresses the unique challenges of calibrating probabilities in analytical chemistry, where signal distributions can vary significantly across different instruments and experimental conditions. Their calibration pipeline includes an automated validation framework that continuously monitors calibration quality and triggers recalibration when drift is detected. This is particularly important for maintaining consistent performance across their global instrument fleet. Agilent has also developed specialized calibration techniques for handling the extreme class imbalance common in analytical applications, where the vast majority of potential compounds are absent from any given sample. Their approach includes a hierarchical sigmoid transformation that provides well-calibrated probabilities across multiple orders of magnitude, essential for trace compound detection applications.
Strengths: Domain-optimized calibration specifically designed for analytical chemistry applications; robust performance across different instrument configurations and experimental conditions. Weaknesses: Highly specialized approach that may not generalize well to other domains; requires significant domain expertise to properly implement and maintain.
Oracle International Corp.
Technical Solution: Oracle has developed advanced probability calibration techniques for their machine learning services within Oracle Cloud Infrastructure (OCI). Their approach combines Platt Scaling and Temperature Scaling methods to improve the reliability of probabilistic predictions across their database and analytics products. Oracle's implementation uses sigmoid functions to transform uncalibrated model outputs into well-calibrated probabilities, particularly important for their decision support systems. Their Data Science platform incorporates automated calibration pipelines that dynamically select between Platt Scaling for binary classification problems and Temperature Scaling for multi-class scenarios. This calibration framework is integrated into Oracle's AutoML capabilities, allowing automatic post-processing of model outputs to ensure reliable probability estimates without requiring manual intervention from data scientists. Oracle has also developed specialized calibration techniques for time-series forecasting models used in their supply chain and financial applications.
Strengths: Seamless integration with existing Oracle database and analytics ecosystem; enterprise-scale implementation with proven reliability in high-stakes business applications. Weaknesses: Proprietary implementation limits academic scrutiny; potentially higher computational overhead compared to simpler approaches when deployed at scale.
Technical Analysis of Sigmoid-Based Calibration Algorithms
Method for optimizing an optical aid by way of automatic subjective visual performance measurement
PatentActiveUS20210157168A1
Innovation
- A method utilizing machine learning to automatically determine subjective visual acuity by training an artificial neural network with a training data set, parameterizing stimulus images, and adapting parameterizations to optimize optical aids for improved visual acuity.
Hidden sigmoid function calculation system, hidden logistic regression calculation system, hidden sigmoid function calculation device, hidden logistic regression calculation device, hidden sigmoid function calculation method, hidden logistic regression calculation method, and program
PatentWO2020071187A1
Innovation
- A secret sigmoid function calculation system and method that utilizes a combination of secure computation operations like masking, addition, multiplication, magnitude comparison, and logical operations to calculate the sigmoid function with high accuracy and speed, employing an approximate sigmoid function defined by specific thresholds and a linear function g(x) for efficient computation.
Benchmarking and Evaluation Metrics for Calibration Methods
Evaluating the effectiveness of probability calibration methods requires robust benchmarking frameworks and appropriate metrics. The reliability diagram serves as a fundamental visualization tool, plotting predicted probabilities against observed frequencies to identify calibration errors. Perfect calibration appears as points along the diagonal, while deviations indicate over or under-confidence.
Expected Calibration Error (ECE) has emerged as the de facto standard metric, partitioning predictions into bins and measuring the weighted average difference between predicted probabilities and observed frequencies. This metric effectively quantifies overall calibration performance but may mask localized calibration issues in specific probability ranges.
Maximum Calibration Error (MCE) complements ECE by identifying the worst-case calibration error across all bins, providing insight into the most severe calibration failures. This metric is particularly valuable for applications where reliability in high-confidence predictions is critical.
Brier Score offers a comprehensive evaluation by simultaneously measuring calibration, refinement, and uncertainty. Unlike ECE and MCE, it doesn't require binning, making it less sensitive to binning strategies and more suitable for continuous evaluation.
Negative Log-Likelihood (NLL) serves as both a training objective and evaluation metric, penalizing miscalibrated probabilities more severely as confidence increases. This property makes NLL particularly effective for detecting overconfident predictions.
Cross-dataset evaluation represents a critical dimension in calibration assessment. Methods like Platt Scaling and Temperature Scaling often demonstrate varying performance when tested on datasets different from their training distribution. Recent research indicates Temperature Scaling generally maintains better calibration properties under distribution shift compared to Platt Scaling.
Time-series evaluation provides another important perspective, especially for applications where calibration stability over time is essential. Methods exhibiting temporal robustness are increasingly valued in production environments where data distributions evolve.
Computational efficiency metrics, including training time, inference overhead, and memory requirements, have gained prominence as calibration methods move from research to production. Temperature Scaling maintains an advantage in this domain due to its single-parameter optimization approach compared to the more complex Platt Scaling.
Recent benchmarking efforts have established standardized evaluation protocols, enabling fair comparison across calibration methods and application domains. These protocols typically incorporate multiple metrics and diverse datasets to provide a holistic assessment of calibration performance.
Expected Calibration Error (ECE) has emerged as the de facto standard metric, partitioning predictions into bins and measuring the weighted average difference between predicted probabilities and observed frequencies. This metric effectively quantifies overall calibration performance but may mask localized calibration issues in specific probability ranges.
Maximum Calibration Error (MCE) complements ECE by identifying the worst-case calibration error across all bins, providing insight into the most severe calibration failures. This metric is particularly valuable for applications where reliability in high-confidence predictions is critical.
Brier Score offers a comprehensive evaluation by simultaneously measuring calibration, refinement, and uncertainty. Unlike ECE and MCE, it doesn't require binning, making it less sensitive to binning strategies and more suitable for continuous evaluation.
Negative Log-Likelihood (NLL) serves as both a training objective and evaluation metric, penalizing miscalibrated probabilities more severely as confidence increases. This property makes NLL particularly effective for detecting overconfident predictions.
Cross-dataset evaluation represents a critical dimension in calibration assessment. Methods like Platt Scaling and Temperature Scaling often demonstrate varying performance when tested on datasets different from their training distribution. Recent research indicates Temperature Scaling generally maintains better calibration properties under distribution shift compared to Platt Scaling.
Time-series evaluation provides another important perspective, especially for applications where calibration stability over time is essential. Methods exhibiting temporal robustness are increasingly valued in production environments where data distributions evolve.
Computational efficiency metrics, including training time, inference overhead, and memory requirements, have gained prominence as calibration methods move from research to production. Temperature Scaling maintains an advantage in this domain due to its single-parameter optimization approach compared to the more complex Platt Scaling.
Recent benchmarking efforts have established standardized evaluation protocols, enabling fair comparison across calibration methods and application domains. These protocols typically incorporate multiple metrics and diverse datasets to provide a holistic assessment of calibration performance.
Integration Challenges in Production ML Systems
Integrating probability calibration techniques such as Sigmoid Function, Platt Scaling, and Temperature Scaling into production machine learning systems presents several significant challenges that organizations must address. The fundamental issue lies in the transition from controlled development environments to dynamic production settings where data distributions frequently shift. When deploying calibration methods in production, engineering teams often encounter computational overhead concerns, particularly with Platt Scaling which requires maintaining a separate validation dataset and additional model training steps.
Real-time calibration poses another substantial challenge, as production systems typically demand immediate predictions. Temperature Scaling, while computationally efficient, may require periodic recalibration as production data evolves, necessitating sophisticated monitoring systems to detect when recalibration is needed. This creates a complex balance between prediction speed and calibration accuracy that must be carefully managed.
Version control becomes increasingly complex when calibration layers are introduced. Organizations must track not only the base model versions but also the calibration parameters, creating interdependencies that complicate rollback procedures and A/B testing frameworks. This version complexity extends to monitoring systems, which must distinguish between base model performance issues and calibration layer problems.
Infrastructure requirements present additional hurdles, as calibration methods like Platt Scaling demand separate validation datasets that must be maintained, updated, and properly stored within production environments. This increases storage requirements and adds complexity to data pipeline management. Furthermore, the calibration process itself may introduce latency in prediction services, potentially affecting service level agreements (SLAs) in time-sensitive applications.
Model interpretability can be compromised when calibration layers are added to production systems. While the original model might have clear feature importance metrics, the post-calibration behavior may become less transparent, creating challenges for regulatory compliance and stakeholder trust. This is particularly problematic in highly regulated industries where model explainability is mandated.
Finally, the integration of calibration techniques requires specialized knowledge that may not be widely available within engineering teams. This expertise gap can lead to implementation errors or suboptimal calibration strategies, highlighting the need for comprehensive documentation and training programs when deploying these sophisticated probability calibration methods in production machine learning systems.
Real-time calibration poses another substantial challenge, as production systems typically demand immediate predictions. Temperature Scaling, while computationally efficient, may require periodic recalibration as production data evolves, necessitating sophisticated monitoring systems to detect when recalibration is needed. This creates a complex balance between prediction speed and calibration accuracy that must be carefully managed.
Version control becomes increasingly complex when calibration layers are introduced. Organizations must track not only the base model versions but also the calibration parameters, creating interdependencies that complicate rollback procedures and A/B testing frameworks. This version complexity extends to monitoring systems, which must distinguish between base model performance issues and calibration layer problems.
Infrastructure requirements present additional hurdles, as calibration methods like Platt Scaling demand separate validation datasets that must be maintained, updated, and properly stored within production environments. This increases storage requirements and adds complexity to data pipeline management. Furthermore, the calibration process itself may introduce latency in prediction services, potentially affecting service level agreements (SLAs) in time-sensitive applications.
Model interpretability can be compromised when calibration layers are added to production systems. While the original model might have clear feature importance metrics, the post-calibration behavior may become less transparent, creating challenges for regulatory compliance and stakeholder trust. This is particularly problematic in highly regulated industries where model explainability is mandated.
Finally, the integration of calibration techniques requires specialized knowledge that may not be widely available within engineering teams. This expertise gap can lead to implementation errors or suboptimal calibration strategies, highlighting the need for comprehensive documentation and training programs when deploying these sophisticated probability calibration methods in production machine learning systems.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!