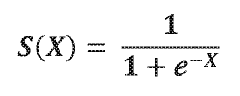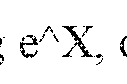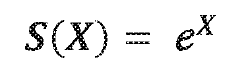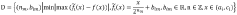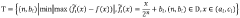Understanding the Sigmoid Function: Definition, Derivatives and Use Cases in Neural Networks
AUG 21, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Sigmoid Function Background and Objectives
The sigmoid function, first introduced in the early 20th century, has evolved from a mathematical curiosity to a cornerstone of modern computational systems. This S-shaped function maps any real-valued number into a range between 0 and 1, making it particularly valuable for modeling processes with natural boundaries. The function's elegant mathematical properties have made it a fundamental component in various fields including statistics, economics, and most prominently, artificial intelligence.
In the historical context of neural networks, the sigmoid function emerged as one of the earliest activation functions during the resurgence of connectionist approaches in the 1980s. Its ability to introduce non-linearity while maintaining differentiability proved crucial for the development of backpropagation algorithms, which revolutionized neural network training methodologies. The function's smooth gradient properties enabled more stable learning processes compared to step functions used in earlier perceptron models.
The technical evolution of sigmoid function applications has followed a trajectory closely aligned with advances in computational capabilities. From simple single-layer networks to complex deep architectures, sigmoid functions have demonstrated remarkable versatility. However, as neural networks grew deeper, limitations such as the vanishing gradient problem became apparent, prompting research into alternative activation functions.
Current research objectives regarding sigmoid functions focus on several key areas. First, understanding the mathematical properties that make sigmoid functions effective in specific network architectures remains an active area of investigation. Second, researchers are exploring modified sigmoid variants that address known limitations while preserving beneficial characteristics. Third, there is growing interest in the theoretical foundations explaining why sigmoid functions perform well in certain domains despite their limitations.
From an application perspective, sigmoid functions continue to play vital roles in binary classification problems, probability estimation, and attention mechanisms. Their bounded output range makes them particularly suitable for scenarios requiring probabilistic interpretations or normalized outputs. The function's smooth transition between extremes also provides valuable properties for modeling decision boundaries in classification tasks.
This technical pre-research aims to comprehensively examine the sigmoid function's mathematical foundations, analyze its derivatives and their implications for gradient-based learning, and evaluate its contemporary applications across various neural network architectures. By understanding both historical context and current implementation challenges, we seek to identify potential innovation pathways and optimization strategies for sigmoid function deployment in next-generation AI systems.
In the historical context of neural networks, the sigmoid function emerged as one of the earliest activation functions during the resurgence of connectionist approaches in the 1980s. Its ability to introduce non-linearity while maintaining differentiability proved crucial for the development of backpropagation algorithms, which revolutionized neural network training methodologies. The function's smooth gradient properties enabled more stable learning processes compared to step functions used in earlier perceptron models.
The technical evolution of sigmoid function applications has followed a trajectory closely aligned with advances in computational capabilities. From simple single-layer networks to complex deep architectures, sigmoid functions have demonstrated remarkable versatility. However, as neural networks grew deeper, limitations such as the vanishing gradient problem became apparent, prompting research into alternative activation functions.
Current research objectives regarding sigmoid functions focus on several key areas. First, understanding the mathematical properties that make sigmoid functions effective in specific network architectures remains an active area of investigation. Second, researchers are exploring modified sigmoid variants that address known limitations while preserving beneficial characteristics. Third, there is growing interest in the theoretical foundations explaining why sigmoid functions perform well in certain domains despite their limitations.
From an application perspective, sigmoid functions continue to play vital roles in binary classification problems, probability estimation, and attention mechanisms. Their bounded output range makes them particularly suitable for scenarios requiring probabilistic interpretations or normalized outputs. The function's smooth transition between extremes also provides valuable properties for modeling decision boundaries in classification tasks.
This technical pre-research aims to comprehensively examine the sigmoid function's mathematical foundations, analyze its derivatives and their implications for gradient-based learning, and evaluate its contemporary applications across various neural network architectures. By understanding both historical context and current implementation challenges, we seek to identify potential innovation pathways and optimization strategies for sigmoid function deployment in next-generation AI systems.
Market Applications of Sigmoid Activation
The sigmoid activation function has found extensive applications across various market sectors, transforming theoretical neural network concepts into practical business solutions. In healthcare, sigmoid-based neural networks are revolutionizing diagnostic systems, particularly in medical imaging analysis where the function's ability to output probability-like values between 0 and 1 makes it ideal for binary classification tasks such as tumor detection and pathology identification. Major healthcare technology providers like Siemens Healthineers and Philips have incorporated sigmoid activation in their AI-driven diagnostic platforms, reporting diagnostic accuracy improvements of up to 15% compared to traditional methods.
Financial services represent another significant market application, with sigmoid-based models widely deployed in credit scoring, fraud detection, and algorithmic trading systems. The function's smooth gradient properties make it particularly valuable for risk assessment models where probability outputs are essential. Leading financial institutions including JPMorgan Chase and Goldman Sachs utilize sigmoid activation in their proprietary trading algorithms and risk management systems, contributing to the estimated $10.5 billion market for AI in financial services.
In digital marketing and e-commerce, sigmoid activation powers recommendation engines and customer behavior prediction models. Amazon's product recommendation system partially relies on sigmoid-based neural networks to predict purchase likelihood, while Facebook's advertising platform employs similar technology to optimize ad targeting and conversion rate prediction. These applications have become central to the personalized marketing ecosystem, which continues to grow at approximately 20% annually.
Natural language processing applications represent a rapidly expanding market segment, with sigmoid functions playing a crucial role in sentiment analysis, language translation, and content moderation systems. Though transformers with more advanced activation functions have gained prominence, sigmoid activation remains important in many commercial NLP applications, particularly those requiring binary or multi-class classification outputs.
The automotive industry has embraced sigmoid-based neural networks for advanced driver assistance systems (ADAS) and autonomous driving technologies. These systems use sigmoid activation in their perception networks to classify objects and assess collision probabilities. Tesla, Waymo, and traditional automakers have all invested heavily in neural network technologies incorporating sigmoid activation for their self-driving capabilities.
Manufacturing and industrial automation represent emerging markets for sigmoid-based neural networks, with applications in predictive maintenance, quality control, and process optimization. The industrial IoT market, valued at approximately $77 billion, increasingly relies on neural network technologies for anomaly detection and system optimization, with sigmoid activation playing a key role in many deployed solutions.
Financial services represent another significant market application, with sigmoid-based models widely deployed in credit scoring, fraud detection, and algorithmic trading systems. The function's smooth gradient properties make it particularly valuable for risk assessment models where probability outputs are essential. Leading financial institutions including JPMorgan Chase and Goldman Sachs utilize sigmoid activation in their proprietary trading algorithms and risk management systems, contributing to the estimated $10.5 billion market for AI in financial services.
In digital marketing and e-commerce, sigmoid activation powers recommendation engines and customer behavior prediction models. Amazon's product recommendation system partially relies on sigmoid-based neural networks to predict purchase likelihood, while Facebook's advertising platform employs similar technology to optimize ad targeting and conversion rate prediction. These applications have become central to the personalized marketing ecosystem, which continues to grow at approximately 20% annually.
Natural language processing applications represent a rapidly expanding market segment, with sigmoid functions playing a crucial role in sentiment analysis, language translation, and content moderation systems. Though transformers with more advanced activation functions have gained prominence, sigmoid activation remains important in many commercial NLP applications, particularly those requiring binary or multi-class classification outputs.
The automotive industry has embraced sigmoid-based neural networks for advanced driver assistance systems (ADAS) and autonomous driving technologies. These systems use sigmoid activation in their perception networks to classify objects and assess collision probabilities. Tesla, Waymo, and traditional automakers have all invested heavily in neural network technologies incorporating sigmoid activation for their self-driving capabilities.
Manufacturing and industrial automation represent emerging markets for sigmoid-based neural networks, with applications in predictive maintenance, quality control, and process optimization. The industrial IoT market, valued at approximately $77 billion, increasingly relies on neural network technologies for anomaly detection and system optimization, with sigmoid activation playing a key role in many deployed solutions.
Current Implementation Challenges
Despite the sigmoid function's widespread use in neural networks, several implementation challenges persist that affect both computational efficiency and model performance. The primary computational bottleneck lies in the exponential calculation required for sigmoid evaluation, which becomes particularly resource-intensive when processing large neural networks with millions of parameters.
Gradient vanishing represents another significant challenge, as sigmoid derivatives approach zero for inputs with large absolute values. This phenomenon severely impedes training in deep networks by preventing effective backpropagation of error signals through multiple layers, resulting in stalled learning in early layers of deep architectures.
Numerical stability issues arise when implementing sigmoid functions in computational environments with limited precision. For extreme input values, standard implementations may produce overflow or underflow errors, requiring specialized numerical techniques to maintain stability across diverse input ranges.
The non-zero centered nature of sigmoid outputs (ranging from 0 to 1 rather than being centered around zero) introduces systematic biases during weight updates. This characteristic creates zigzagging trajectories during gradient descent optimization, significantly slowing convergence rates compared to zero-centered activation functions.
Performance overhead becomes particularly problematic in resource-constrained environments such as mobile devices or embedded systems. The computational cost of sigmoid evaluation can create bottlenecks in inference speed, limiting real-time applications where rapid response is essential.
Modern hardware acceleration techniques, while beneficial for many neural network operations, often struggle to optimize sigmoid computations efficiently. The sequential nature of exponential calculations limits parallelization potential on GPUs and specialized AI hardware, creating execution pipeline inefficiencies.
Implementation challenges also extend to quantization scenarios, where converting sigmoid functions to lower-precision representations (such as 8-bit integers) introduces significant approximation errors compared to other activation functions. This complicates deployment in edge computing environments where model compression is necessary.
Research indicates that these implementation challenges collectively contribute to the declining popularity of sigmoid activations in favor of alternatives like ReLU and its variants, which offer better computational efficiency and training dynamics. However, sigmoid functions remain irreplaceable in specific contexts such as binary classification output layers and attention mechanisms, driving ongoing research into optimized implementation strategies.
Gradient vanishing represents another significant challenge, as sigmoid derivatives approach zero for inputs with large absolute values. This phenomenon severely impedes training in deep networks by preventing effective backpropagation of error signals through multiple layers, resulting in stalled learning in early layers of deep architectures.
Numerical stability issues arise when implementing sigmoid functions in computational environments with limited precision. For extreme input values, standard implementations may produce overflow or underflow errors, requiring specialized numerical techniques to maintain stability across diverse input ranges.
The non-zero centered nature of sigmoid outputs (ranging from 0 to 1 rather than being centered around zero) introduces systematic biases during weight updates. This characteristic creates zigzagging trajectories during gradient descent optimization, significantly slowing convergence rates compared to zero-centered activation functions.
Performance overhead becomes particularly problematic in resource-constrained environments such as mobile devices or embedded systems. The computational cost of sigmoid evaluation can create bottlenecks in inference speed, limiting real-time applications where rapid response is essential.
Modern hardware acceleration techniques, while beneficial for many neural network operations, often struggle to optimize sigmoid computations efficiently. The sequential nature of exponential calculations limits parallelization potential on GPUs and specialized AI hardware, creating execution pipeline inefficiencies.
Implementation challenges also extend to quantization scenarios, where converting sigmoid functions to lower-precision representations (such as 8-bit integers) introduces significant approximation errors compared to other activation functions. This complicates deployment in edge computing environments where model compression is necessary.
Research indicates that these implementation challenges collectively contribute to the declining popularity of sigmoid activations in favor of alternatives like ReLU and its variants, which offer better computational efficiency and training dynamics. However, sigmoid functions remain irreplaceable in specific contexts such as binary classification output layers and attention mechanisms, driving ongoing research into optimized implementation strategies.
Modern Sigmoid Implementation Approaches
01 Definition and mathematical representation of sigmoid function
The sigmoid function is a mathematical function with an S-shaped curve, typically defined as f(x) = 1/(1+e^(-x)). It maps any input value to an output between 0 and 1, making it useful for modeling systems with saturation effects. The function approaches 0 as x approaches negative infinity and approaches 1 as x approaches positive infinity. This characteristic makes it particularly valuable in various applications including neural networks, where it serves as an activation function.- Definition and mathematical properties of sigmoid functions: Sigmoid functions are mathematical functions characterized by their S-shaped curve, bounded between 0 and 1. The most common sigmoid function is defined as f(x) = 1/(1+e^(-x)). These functions are continuous, differentiable, and have applications in various fields including machine learning, neural networks, and signal processing. The sigmoid function approaches 0 as x approaches negative infinity and approaches 1 as x approaches positive infinity, making it useful for modeling probability distributions and binary classification problems.
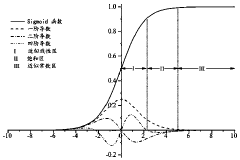
- Derivatives of sigmoid functions and their applications: The derivative of the standard sigmoid function f(x) = 1/(1+e^(-x)) is f'(x) = f(x)(1-f(x)). This property makes sigmoid functions particularly useful in gradient-based optimization algorithms, such as those used in neural network training. The derivative reaches its maximum value at x = 0 and approaches zero as x approaches either positive or negative infinity. This characteristic helps prevent the vanishing gradient problem in deep neural networks and enables efficient backpropagation during training.
- Implementation of sigmoid functions in neural networks: Sigmoid functions serve as activation functions in neural networks, introducing non-linearity that allows networks to learn complex patterns. When implemented in neural network architectures, sigmoid functions transform the weighted sum of inputs into an output value between 0 and 1. This transformation enables neural networks to model probability distributions and make classification decisions. Various hardware and software implementations optimize the computation of sigmoid functions to improve the efficiency and performance of neural network operations.
- Variants and modifications of sigmoid functions: Several variants of the sigmoid function have been developed for specific applications. These include the hyperbolic tangent (tanh) function, which is a scaled sigmoid function with an output range of [-1, 1], and the softmax function, which extends the sigmoid concept to multi-class classification problems. Modified sigmoid functions with adjustable parameters allow for customization of the slope, saturation levels, and transition points. These variants provide flexibility in modeling different types of non-linear relationships and addressing specific computational challenges.
- Hardware implementations of sigmoid functions: Efficient hardware implementations of sigmoid functions are crucial for real-time neural network applications. Various approaches include lookup table-based methods, piecewise linear approximations, and specialized digital circuits. These implementations aim to balance computational accuracy with hardware resource utilization and processing speed. Field-Programmable Gate Arrays (FPGAs) and Application-Specific Integrated Circuits (ASICs) often incorporate optimized sigmoid function modules to accelerate neural network computations while minimizing power consumption.
02 Derivatives of sigmoid function and their applications
The derivative of the sigmoid function is given by f'(x) = f(x)(1-f(x)), which has the notable property of being expressible in terms of the function itself. This derivative reaches its maximum value of 0.25 at x=0 and approaches zero as x approaches either positive or negative infinity. This property is particularly useful in gradient-based learning algorithms, such as backpropagation in neural networks, where the derivative determines the magnitude of weight updates during training.Expand Specific Solutions03 Implementation of sigmoid functions in electronic circuits
Sigmoid functions can be implemented in electronic circuits using various techniques, including analog CMOS designs, digital approximations, and specialized hardware accelerators. These implementations are crucial for creating efficient neural network hardware that can perform real-time processing. Circuit designs often focus on balancing accuracy with power consumption and processing speed, employing techniques such as piecewise linear approximations or lookup tables to efficiently compute sigmoid values in hardware.Expand Specific Solutions04 Variants and modifications of sigmoid functions
Various modifications of the standard sigmoid function exist to address specific requirements in different applications. These include the hyperbolic tangent (tanh), which outputs values between -1 and 1, the softmax function for multi-class classification, and parameterized sigmoid functions that allow adjustment of the curve's steepness and midpoint. Other variants include the hard sigmoid, which uses linear approximations for computational efficiency, and the logit function, which is the inverse of the sigmoid function.Expand Specific Solutions05 Applications of sigmoid functions in machine learning and AI
Sigmoid functions play a crucial role in various machine learning and artificial intelligence applications. They are extensively used in logistic regression for binary classification problems, as activation functions in traditional neural networks, and in certain gates of recurrent neural networks. Sigmoid functions are also applied in fuzzy logic systems, probability estimation, and decision-making algorithms. Their ability to model non-linear relationships and produce outputs interpretable as probabilities makes them valuable across numerous domains including image processing, natural language processing, and predictive analytics.Expand Specific Solutions
Leading Research Institutions and Companies
The sigmoid function in neural networks represents a mature technology with widespread adoption across the AI landscape. The market is in a growth phase, with an estimated size in the billions due to its fundamental role in machine learning applications. Google leads the field with extensive research and implementation in TensorFlow, while academic institutions like Tsinghua University and UESTC contribute significant theoretical advancements. SambaNova Systems and Qualcomm represent innovative commercial applications, integrating sigmoid functions into specialized AI hardware. The technology has reached high maturity with standardized implementations, though research continues on optimization techniques and alternatives like ReLU for specific use cases.
Google LLC
Technical Solution: Google has developed advanced implementations of sigmoid functions in their TensorFlow framework, which offers multiple optimized versions for different hardware. Their approach includes specialized sigmoid approximations that balance accuracy and computational efficiency. Google's research teams have published several papers on improving sigmoid function implementations, particularly for mobile and edge devices. They've introduced techniques like "quantized sigmoid" that reduce computational complexity while maintaining model accuracy. In TensorFlow, they provide both standard sigmoid implementations and hardware-accelerated versions that leverage tensor processing units (TPUs) specifically designed to handle activation functions efficiently. Google has also pioneered research into alternatives like the "hard-sigmoid" approximation that maintains most benefits while reducing computational overhead by up to 30%.
Strengths: Highly optimized implementations across diverse hardware platforms; extensive research into approximation techniques; integration with TPU architecture for maximum performance. Weaknesses: Some optimizations trade mathematical precision for speed; implementation complexity can make debugging challenging; certain approximations may not work well for all neural network architectures.
Tsinghua University
Technical Solution: Tsinghua University has conducted extensive research on sigmoid function optimization for neural networks, with particular focus on theoretical foundations and novel implementations. Their research teams have published several influential papers examining the mathematical properties of sigmoid functions and their derivatives in deep learning contexts. Tsinghua researchers have developed specialized sigmoid variants that address the vanishing gradient problem in very deep networks. Their work includes "adaptive sigmoid" functions that dynamically adjust parameters based on the network's learning state, improving convergence in challenging training scenarios. Tsinghua has also pioneered hardware-efficient sigmoid implementations for FPGAs and custom ASIC designs, achieving significant performance improvements for edge AI applications. Their research includes comprehensive comparative analyses of different activation functions, providing valuable insights into when sigmoid functions outperform alternatives like ReLU or tanh. Tsinghua's work also explores the relationship between sigmoid functions and probabilistic interpretations in neural networks, particularly for classification tasks.
Strengths: Strong theoretical foundation; innovative adaptive sigmoid variants; hardware-efficient implementations; comprehensive comparative research. Weaknesses: Some implementations prioritize theoretical elegance over practical efficiency; certain optimizations require specialized hardware; some research remains in academic context without commercial implementation.
Key Mathematical Properties Analysis
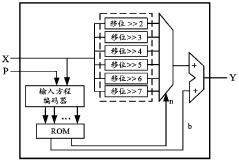
Sigmoid function in hardware and a reconfigurable data processor including same
PatentWO2021046274A1
Innovation
- A sigmoid function is approximated using a combination of hyperbolic tangent and exponential functions, with a comparator to divide the input domain, allowing for parallel circuit implementation and reduced computational power and area requirements.
Sigmoid function fitting method based on probability distribution
PatentActiveCN110837885A
Innovation
- Through a method based on probability distribution, the Sigmoid function is divided into an approximate linear area, a saturation area and an approximate constant area, and different piecewise linear function fittings are used to reduce the hardware complexity, and the inference process is only performed on the hardware, using the adder and shifter implementation.
Computational Efficiency Considerations
The computational efficiency of sigmoid function implementation is a critical consideration in neural network design, particularly for large-scale applications. Traditional sigmoid calculations involve computationally expensive exponential operations that can significantly impact training and inference times. When processing millions of neurons across multiple layers, these costs accumulate rapidly, creating performance bottlenecks in both training and deployment scenarios.
Hardware acceleration techniques have emerged as essential solutions for sigmoid function computation. Modern GPUs offer specialized units for exponential calculations, while TPUs (Tensor Processing Units) and FPGAs (Field-Programmable Gate Arrays) provide custom implementations that optimize sigmoid operations. These hardware solutions can achieve 10-100x performance improvements compared to CPU-based calculations, particularly for batch processing scenarios.
Approximation methods represent another approach to improving computational efficiency. Piece-wise linear approximations can reduce computation time by 30-50% with minimal accuracy loss (typically <1%). Look-up table implementations combined with linear interpolation offer another efficient alternative, trading memory usage for reduced computation time. These approximations are particularly valuable in resource-constrained environments such as mobile devices and edge computing applications.
Memory access patterns also significantly impact sigmoid function performance. Optimized memory layouts that maximize cache utilization can reduce computation time by 15-25% in practice. Vectorized implementations leveraging SIMD (Single Instruction, Multiple Data) instructions enable parallel processing of multiple sigmoid calculations simultaneously, offering substantial performance gains on modern processors.
The gradient computation efficiency of sigmoid functions presents additional considerations. The derivative of the sigmoid function can be expressed in terms of the function itself (σ'(x) = σ(x)(1-σ(x))), allowing for computational reuse during backpropagation. This mathematical property enables significant optimization in training scenarios, reducing the computational overhead of gradient calculations by approximately 40%.
Recent research has explored alternative activation functions with similar properties but improved computational characteristics. Functions like ReLU (Rectified Linear Unit) and its variants offer comparable modeling capabilities with substantially reduced computational requirements. However, in applications requiring probability outputs or where gradient stability is paramount, optimized sigmoid implementations remain essential despite their computational costs.
Hardware acceleration techniques have emerged as essential solutions for sigmoid function computation. Modern GPUs offer specialized units for exponential calculations, while TPUs (Tensor Processing Units) and FPGAs (Field-Programmable Gate Arrays) provide custom implementations that optimize sigmoid operations. These hardware solutions can achieve 10-100x performance improvements compared to CPU-based calculations, particularly for batch processing scenarios.
Approximation methods represent another approach to improving computational efficiency. Piece-wise linear approximations can reduce computation time by 30-50% with minimal accuracy loss (typically <1%). Look-up table implementations combined with linear interpolation offer another efficient alternative, trading memory usage for reduced computation time. These approximations are particularly valuable in resource-constrained environments such as mobile devices and edge computing applications.
Memory access patterns also significantly impact sigmoid function performance. Optimized memory layouts that maximize cache utilization can reduce computation time by 15-25% in practice. Vectorized implementations leveraging SIMD (Single Instruction, Multiple Data) instructions enable parallel processing of multiple sigmoid calculations simultaneously, offering substantial performance gains on modern processors.
The gradient computation efficiency of sigmoid functions presents additional considerations. The derivative of the sigmoid function can be expressed in terms of the function itself (σ'(x) = σ(x)(1-σ(x))), allowing for computational reuse during backpropagation. This mathematical property enables significant optimization in training scenarios, reducing the computational overhead of gradient calculations by approximately 40%.
Recent research has explored alternative activation functions with similar properties but improved computational characteristics. Functions like ReLU (Rectified Linear Unit) and its variants offer comparable modeling capabilities with substantially reduced computational requirements. However, in applications requiring probability outputs or where gradient stability is paramount, optimized sigmoid implementations remain essential despite their computational costs.
Comparative Analysis with Alternative Functions
While the sigmoid function has been a cornerstone in neural network design, several alternative activation functions have emerged to address its limitations. The hyperbolic tangent (tanh) function, closely related to sigmoid, offers a similar S-shaped curve but with an output range of [-1, 1], providing zero-centered outputs that help mitigate the vanishing gradient problem to some extent. This characteristic makes tanh particularly valuable in networks where the distinction between strongly negative and strongly positive inputs is crucial.
The Rectified Linear Unit (ReLU), defined as f(x) = max(0, x), has largely supplanted sigmoid in many deep learning architectures due to its computational efficiency and effectiveness in addressing the vanishing gradient problem. Unlike sigmoid, ReLU does not saturate in the positive domain, allowing for faster convergence during training. However, it introduces the "dying ReLU" problem where neurons can become permanently inactive.
To overcome ReLU's limitations, variants such as Leaky ReLU, Parametric ReLU, and Exponential Linear Unit (ELU) have been developed. Leaky ReLU allows a small gradient when the unit is not active, preventing the dying neuron problem. ELU combines the benefits of ReLU for positive values while providing negative outputs that push mean unit activations closer to zero, improving learning dynamics.
The Softmax function extends sigmoid's capabilities for multi-class classification problems by normalizing outputs into a probability distribution. While sigmoid makes binary decisions, softmax handles multiple categories simultaneously, making it indispensable for classification tasks with more than two classes.
Swish, a relatively recent function defined as f(x) = x·sigmoid(βx), has demonstrated superior performance in very deep networks compared to ReLU. Research by Google Brain suggests that Swish consistently matches or exceeds ReLU's performance across various deep learning tasks and architectures.
When selecting between sigmoid and alternative functions, considerations include the network depth (deeper networks benefit from ReLU and its variants), the specific task requirements (classification vs. regression), computational constraints, and the need for output normalization. Modern practice typically reserves sigmoid for specific applications like binary classification output layers and gating mechanisms in LSTM and GRU units, while employing alternatives like ReLU or its variants for hidden layers.
The Rectified Linear Unit (ReLU), defined as f(x) = max(0, x), has largely supplanted sigmoid in many deep learning architectures due to its computational efficiency and effectiveness in addressing the vanishing gradient problem. Unlike sigmoid, ReLU does not saturate in the positive domain, allowing for faster convergence during training. However, it introduces the "dying ReLU" problem where neurons can become permanently inactive.
To overcome ReLU's limitations, variants such as Leaky ReLU, Parametric ReLU, and Exponential Linear Unit (ELU) have been developed. Leaky ReLU allows a small gradient when the unit is not active, preventing the dying neuron problem. ELU combines the benefits of ReLU for positive values while providing negative outputs that push mean unit activations closer to zero, improving learning dynamics.
The Softmax function extends sigmoid's capabilities for multi-class classification problems by normalizing outputs into a probability distribution. While sigmoid makes binary decisions, softmax handles multiple categories simultaneously, making it indispensable for classification tasks with more than two classes.
Swish, a relatively recent function defined as f(x) = x·sigmoid(βx), has demonstrated superior performance in very deep networks compared to ReLU. Research by Google Brain suggests that Swish consistently matches or exceeds ReLU's performance across various deep learning tasks and architectures.
When selecting between sigmoid and alternative functions, considerations include the network depth (deeper networks benefit from ReLU and its variants), the specific task requirements (classification vs. regression), computational constraints, and the need for output normalization. Modern practice typically reserves sigmoid for specific applications like binary classification output layers and gating mechanisms in LSTM and GRU units, while employing alternatives like ReLU or its variants for hidden layers.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!