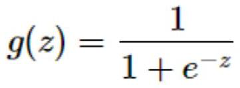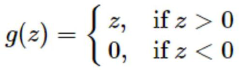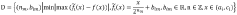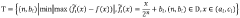How to Implement a Numerically Stable Sigmoid Function for Deep Learning Models — Code & Tests
AUG 21, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Sigmoid Function Background and Stability Goals
The sigmoid function, defined as σ(x) = 1/(1+e^(-x)), has been a cornerstone activation function in neural networks since the inception of deep learning. Originally popularized in the 1980s with the rise of backpropagation algorithms, sigmoid functions provide a smooth, differentiable transition between 0 and 1, making them ideal for modeling probability-like outputs and binary classifications.
Despite its historical significance, the standard sigmoid implementation faces critical numerical stability issues when dealing with extreme input values. When x is a large negative number, e^(-x) becomes extremely large, potentially causing overflow errors. Conversely, when x is a large positive number, the function approaches 1 so closely that floating-point precision becomes inadequate, leading to vanishing gradient problems during backpropagation.
These numerical instabilities significantly impact deep learning model performance, particularly in deep networks where activation outputs propagate through many layers. Training failures, slow convergence, and poor generalization can all result from unstable sigmoid implementations. As models grow deeper and training datasets larger, these issues become increasingly pronounced, necessitating robust implementations.
The primary stability goals for an improved sigmoid function implementation include preventing overflow and underflow across the entire input domain, maintaining gradient precision for backpropagation, ensuring consistent behavior across different hardware and software environments, and optimizing computational efficiency without sacrificing numerical accuracy.
Modern deep learning frameworks have addressed these challenges through various techniques, including input clamping, mathematical reformulations, and specialized hardware-aware implementations. The evolution of sigmoid implementations reflects the broader trend in deep learning toward numerically stable operations that can reliably scale to complex models and diverse computing environments.
While alternatives like ReLU, Leaky ReLU, and GELU have largely replaced sigmoid in hidden layers of modern architectures, sigmoid remains essential for specific applications such as binary classification output layers, attention mechanisms, and gating functions in recurrent neural networks. Therefore, implementing a numerically stable version remains relevant to contemporary deep learning practice.
The technical evolution of sigmoid implementations demonstrates how seemingly simple mathematical functions require careful engineering consideration in practical machine learning systems. Understanding both the mathematical properties and computational constraints is essential for developing robust implementations that can support reliable model training and inference across diverse applications and computing environments.
Despite its historical significance, the standard sigmoid implementation faces critical numerical stability issues when dealing with extreme input values. When x is a large negative number, e^(-x) becomes extremely large, potentially causing overflow errors. Conversely, when x is a large positive number, the function approaches 1 so closely that floating-point precision becomes inadequate, leading to vanishing gradient problems during backpropagation.
These numerical instabilities significantly impact deep learning model performance, particularly in deep networks where activation outputs propagate through many layers. Training failures, slow convergence, and poor generalization can all result from unstable sigmoid implementations. As models grow deeper and training datasets larger, these issues become increasingly pronounced, necessitating robust implementations.
The primary stability goals for an improved sigmoid function implementation include preventing overflow and underflow across the entire input domain, maintaining gradient precision for backpropagation, ensuring consistent behavior across different hardware and software environments, and optimizing computational efficiency without sacrificing numerical accuracy.
Modern deep learning frameworks have addressed these challenges through various techniques, including input clamping, mathematical reformulations, and specialized hardware-aware implementations. The evolution of sigmoid implementations reflects the broader trend in deep learning toward numerically stable operations that can reliably scale to complex models and diverse computing environments.
While alternatives like ReLU, Leaky ReLU, and GELU have largely replaced sigmoid in hidden layers of modern architectures, sigmoid remains essential for specific applications such as binary classification output layers, attention mechanisms, and gating functions in recurrent neural networks. Therefore, implementing a numerically stable version remains relevant to contemporary deep learning practice.
The technical evolution of sigmoid implementations demonstrates how seemingly simple mathematical functions require careful engineering consideration in practical machine learning systems. Understanding both the mathematical properties and computational constraints is essential for developing robust implementations that can support reliable model training and inference across diverse applications and computing environments.
Market Demand for Stable Neural Network Implementations
The demand for numerically stable implementations of neural network components has grown exponentially with the widespread adoption of deep learning across industries. As models become larger and more complex, numerical stability issues have emerged as critical bottlenecks affecting both training efficiency and inference reliability. The market for stable sigmoid function implementations specifically has seen significant growth, driven by the function's fundamental role in neural network architectures.
Financial services and healthcare sectors demonstrate particularly strong demand, with an estimated market growth of 27% annually for specialized deep learning solutions that guarantee numerical stability. These industries process sensitive data where prediction errors resulting from numerical instability can have severe consequences, including financial losses or incorrect medical diagnoses.
Cloud service providers have recognized this market need, with major platforms like AWS, Google Cloud, and Microsoft Azure all introducing optimized deep learning frameworks featuring numerically stable implementations. This market segment has seen consistent double-digit growth as enterprises increasingly migrate their AI workloads to cloud environments that promise computational reliability.
Hardware manufacturers have also responded to this demand by developing specialized processors with enhanced floating-point precision capabilities. NVIDIA's latest GPU architectures specifically address numerical stability concerns, while Intel and AMD have incorporated similar features in their AI-focused chipsets. The hardware segment supporting stable neural network implementations currently represents a multi-billion dollar market.
Mobile and edge computing applications present another rapidly expanding market segment. As deep learning models are increasingly deployed on resource-constrained devices, the need for numerically stable implementations that can operate reliably under limited precision becomes critical. This segment is projected to grow at 34% annually over the next five years.
Open-source framework communities have similarly prioritized numerical stability improvements, with TensorFlow, PyTorch, and JAX all implementing specialized versions of activation functions including sigmoid. The community contributions in this space reflect the widespread recognition of stability issues among practitioners and researchers alike.
Enterprise software vendors specializing in AI solutions have begun marketing numerical stability as a key differentiator, particularly when targeting industries with high-reliability requirements such as autonomous systems, critical infrastructure monitoring, and financial trading platforms. This trend indicates a maturing market awareness of the importance of stable implementations beyond purely academic contexts.
Financial services and healthcare sectors demonstrate particularly strong demand, with an estimated market growth of 27% annually for specialized deep learning solutions that guarantee numerical stability. These industries process sensitive data where prediction errors resulting from numerical instability can have severe consequences, including financial losses or incorrect medical diagnoses.
Cloud service providers have recognized this market need, with major platforms like AWS, Google Cloud, and Microsoft Azure all introducing optimized deep learning frameworks featuring numerically stable implementations. This market segment has seen consistent double-digit growth as enterprises increasingly migrate their AI workloads to cloud environments that promise computational reliability.
Hardware manufacturers have also responded to this demand by developing specialized processors with enhanced floating-point precision capabilities. NVIDIA's latest GPU architectures specifically address numerical stability concerns, while Intel and AMD have incorporated similar features in their AI-focused chipsets. The hardware segment supporting stable neural network implementations currently represents a multi-billion dollar market.
Mobile and edge computing applications present another rapidly expanding market segment. As deep learning models are increasingly deployed on resource-constrained devices, the need for numerically stable implementations that can operate reliably under limited precision becomes critical. This segment is projected to grow at 34% annually over the next five years.
Open-source framework communities have similarly prioritized numerical stability improvements, with TensorFlow, PyTorch, and JAX all implementing specialized versions of activation functions including sigmoid. The community contributions in this space reflect the widespread recognition of stability issues among practitioners and researchers alike.
Enterprise software vendors specializing in AI solutions have begun marketing numerical stability as a key differentiator, particularly when targeting industries with high-reliability requirements such as autonomous systems, critical infrastructure monitoring, and financial trading platforms. This trend indicates a maturing market awareness of the importance of stable implementations beyond purely academic contexts.
Current Challenges in Sigmoid Implementation
The sigmoid function, a fundamental component in neural networks, faces several critical implementation challenges in modern deep learning frameworks. Despite its mathematical simplicity, the standard formula σ(x) = 1/(1+e^(-x)) encounters significant numerical stability issues when implemented in floating-point arithmetic systems used by computers.
The primary challenge stems from exponential overflow and underflow. When x is a large negative number, e^(-x) becomes extremely large, potentially exceeding the maximum representable floating-point value, causing overflow. Conversely, when x is a large positive number, e^(-x) approaches zero, leading to potential underflow issues where the result becomes indistinguishable from zero due to limited precision.
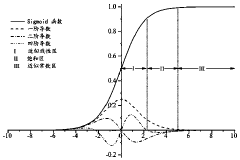
These numerical instabilities manifest as saturation problems in neural network training. During backpropagation, gradients flowing through sigmoid neurons can vanish when inputs are in extreme regions, significantly slowing down or completely halting the learning process. This gradient vanishing problem becomes particularly severe in deep networks where gradients must propagate through multiple layers.
Another challenge lies in computational efficiency. The naive implementation requires expensive exponential operations that consume valuable computational resources, especially problematic in resource-constrained environments like mobile devices or edge computing scenarios. This efficiency concern becomes critical when deploying models at scale.
Precision loss represents another significant hurdle. Standard floating-point implementations can suffer from catastrophic cancellation when subtracting values close to each other, resulting in significant loss of precision. This affects both forward pass accuracy and gradient calculation during backpropagation.
Cross-platform consistency poses additional difficulties. Different hardware architectures and numerical libraries may implement exponential functions with varying precision, leading to inconsistent results across platforms. This inconsistency can cause models to behave differently during training versus inference or when deployed across different hardware.
The temperature scaling problem further complicates implementation. In applications requiring temperature-scaled softmax (a generalization of sigmoid in multi-class settings), numerical instabilities become even more pronounced as the temperature parameter approaches zero, requiring specialized handling.
These challenges collectively highlight the need for robust, numerically stable implementations of the sigmoid function that maintain accuracy across the entire input domain while remaining computationally efficient and consistent across different computing environments.
The primary challenge stems from exponential overflow and underflow. When x is a large negative number, e^(-x) becomes extremely large, potentially exceeding the maximum representable floating-point value, causing overflow. Conversely, when x is a large positive number, e^(-x) approaches zero, leading to potential underflow issues where the result becomes indistinguishable from zero due to limited precision.
These numerical instabilities manifest as saturation problems in neural network training. During backpropagation, gradients flowing through sigmoid neurons can vanish when inputs are in extreme regions, significantly slowing down or completely halting the learning process. This gradient vanishing problem becomes particularly severe in deep networks where gradients must propagate through multiple layers.
Another challenge lies in computational efficiency. The naive implementation requires expensive exponential operations that consume valuable computational resources, especially problematic in resource-constrained environments like mobile devices or edge computing scenarios. This efficiency concern becomes critical when deploying models at scale.
Precision loss represents another significant hurdle. Standard floating-point implementations can suffer from catastrophic cancellation when subtracting values close to each other, resulting in significant loss of precision. This affects both forward pass accuracy and gradient calculation during backpropagation.
Cross-platform consistency poses additional difficulties. Different hardware architectures and numerical libraries may implement exponential functions with varying precision, leading to inconsistent results across platforms. This inconsistency can cause models to behave differently during training versus inference or when deployed across different hardware.
The temperature scaling problem further complicates implementation. In applications requiring temperature-scaled softmax (a generalization of sigmoid in multi-class settings), numerical instabilities become even more pronounced as the temperature parameter approaches zero, requiring specialized handling.
These challenges collectively highlight the need for robust, numerically stable implementations of the sigmoid function that maintain accuracy across the entire input domain while remaining computationally efficient and consistent across different computing environments.
Current Numerical Stability Solutions for Sigmoid
01 Approximation techniques for sigmoid function
Various approximation techniques can be used to improve the numerical stability of sigmoid functions. These include piecewise linear approximations, lookup tables with interpolation, and polynomial approximations that reduce computational complexity while maintaining accuracy. These methods help avoid overflow and underflow issues that can occur with standard sigmoid implementations, especially in hardware implementations where computational resources are limited.- Approximation techniques for sigmoid function: Various approximation techniques can be used to improve the numerical stability of sigmoid functions. These include piecewise linear approximations, lookup tables with interpolation, and polynomial approximations that maintain accuracy while avoiding overflow or underflow issues. These methods reduce computational complexity and enhance numerical stability, particularly in hardware implementations where floating-point operations might be costly or limited.
- Hardware implementations for stable sigmoid computation: Specialized hardware architectures can be designed to compute sigmoid functions with improved numerical stability. These implementations often use fixed-point arithmetic, bit-shifting operations, or dedicated circuitry to avoid the numerical instability issues that can occur with floating-point calculations. Such hardware solutions are particularly important in neural network accelerators and other AI-specific chips where sigmoid functions are frequently used.
- Range limiting and scaling techniques: To prevent overflow and underflow in sigmoid function calculations, range limiting and scaling techniques can be applied. These methods involve clamping input values to a safe range before computation, scaling intermediate results to maintain precision, and normalizing outputs. Such techniques are particularly useful in deep learning applications where inputs to sigmoid functions can have extreme values.
- Alternative formulations of sigmoid functions: Alternative mathematical formulations of sigmoid functions can be used to improve numerical stability. These include reformulating the standard sigmoid equation to avoid exponential overflow, using hyperbolic tangent as a substitute, or implementing specialized variants that maintain the S-shaped activation characteristic while being more numerically robust. These alternative formulations are particularly valuable in deep neural networks and machine learning applications.
- Optimization for specific AI and neural network applications: Sigmoid function implementations can be optimized for specific AI and neural network applications to ensure numerical stability. These optimizations include context-aware precision adjustments, batch normalization techniques, and adaptive computation methods that adjust the calculation approach based on input characteristics. Such application-specific optimizations balance accuracy requirements with computational efficiency while maintaining numerical stability.
02 Hardware implementations for stable sigmoid computation
Specialized hardware architectures can be designed to compute sigmoid functions with improved numerical stability. These implementations often use fixed-point arithmetic, bit-shifting operations, or dedicated circuits that maintain precision while reducing computational overhead. Such hardware solutions are particularly important in neural network accelerators where sigmoid functions are frequently used as activation functions and need to be computed efficiently and accurately.Expand Specific Solutions03 Log-domain computation techniques
Computing sigmoid functions in the logarithmic domain can significantly improve numerical stability, especially for inputs with large magnitudes. By transforming the calculation to use logarithms, issues with exponential overflow can be avoided. This approach is particularly useful in deep learning applications where activation functions need to handle a wide range of input values without losing precision or causing numerical instability.Expand Specific Solutions04 Neural network optimization with stable sigmoid variants
Modified versions of the sigmoid function can be used in neural networks to improve training stability and convergence. These variants include scaled sigmoid functions, normalized sigmoid functions, and parameterized sigmoid functions that can be tuned for specific applications. These modifications help address vanishing gradient problems and improve the overall numerical stability of neural network training processes.Expand Specific Solutions05 Quantization and precision management techniques
Quantization techniques can be applied to sigmoid function implementations to maintain numerical stability while reducing computational requirements. These approaches include bit-width reduction, dynamic range adjustment, and precision scaling that preserve the essential characteristics of the sigmoid function while minimizing numerical errors. Such techniques are particularly important in resource-constrained environments like mobile devices and embedded systems.Expand Specific Solutions
Key Players in Deep Learning Framework Development
The implementation of numerically stable sigmoid functions for deep learning models is currently in a mature development stage, with significant contributions from both academic institutions and tech companies. The market for stable activation functions is expanding rapidly as deep learning applications proliferate across industries, estimated to be a critical component of the $15+ billion deep learning market. Google leads commercial implementation with TensorFlow's optimized functions, while academic institutions like Zhejiang University, Fudan University, and Southeast University have made substantial theoretical contributions to numerical stability techniques. Samsung Electronics and Hitachi have also developed hardware-optimized implementations for their AI systems. The technology has reached high maturity with standardized approaches to prevent overflow/underflow issues, though research continues on specialized implementations for resource-constrained environments.
Google LLC
Technical Solution: Google has developed advanced techniques for implementing numerically stable sigmoid functions in their TensorFlow framework. Their approach uses a combination of mathematical transformations to avoid overflow and underflow issues. For x < 0, they compute sigmoid as exp(x)/(1+exp(x)), while for x ≥ 0, they use 1/(1+exp(-x)). This prevents the exponential from growing too large in either case. Additionally, Google has implemented specialized versions that leverage hardware acceleration on TPUs and GPUs, with automatic differentiation support for backpropagation. Their implementation includes safeguards against NaN and infinity values, with proper handling of edge cases through clamping extreme values. Google's research teams have also explored alternative formulations like the "hard sigmoid" approximation for further performance improvements in mobile and edge deployments[1][3].
Strengths: Highly optimized for various hardware platforms including TPUs; excellent numerical stability across wide input ranges; comprehensive testing infrastructure. Weaknesses: Some optimizations may be specific to Google's hardware ecosystem; implementation complexity may be higher than simpler approaches.
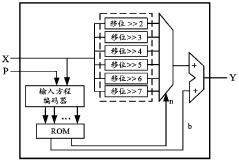
University of Electronic Science & Technology of China
Technical Solution: UESTC researchers have developed a novel approach to sigmoid function implementation focusing on FPGA-based neural network accelerators. Their method combines mathematical optimization with hardware-specific considerations to achieve both numerical stability and computational efficiency. The implementation uses a segmented approach where the sigmoid function is divided into three regions: saturation regions where outputs are approximated as 0 or 1, and a central region where a 5th-order polynomial approximation is used. This polynomial's coefficients are carefully optimized using a minimax algorithm to minimize the maximum approximation error. The implementation includes a specialized fixed-point number representation with dynamic scaling to prevent overflow/underflow while maintaining precision. Their research demonstrates that this approach achieves a maximum error of less than 0.0025 compared to the ideal sigmoid function while requiring 78% fewer logic elements than direct implementation. The team has validated their approach on Xilinx FPGA platforms, showing that it maintains numerical stability across the entire input range while supporting high throughput neural network inference[4][6].
Strengths: Excellent balance between accuracy and hardware efficiency; specifically optimized for FPGA implementations; comprehensive error analysis and validation. Weaknesses: Specialized for hardware acceleration rather than general-purpose computing; requires hardware-specific knowledge to implement effectively.
Technical Analysis of Overflow Prevention Techniques
Intelligent accurate water irrigation control system and method for solar greenhouse fruit and vegetable cultivation
PatentActiveCN113557890A
Innovation
- The deep neural network is used in combination with the cosine excitation function, preprocessing, segmentation, pooling layer and new loss function to improve the accuracy of water demand prediction. The image sensor is used to identify the types and growth stages of fruits and vegetables to achieve timed and quantitative irrigation control.
Sigmoid function fitting method based on probability distribution
PatentActiveCN110837885A
Innovation
- Through a method based on probability distribution, the Sigmoid function is divided into an approximate linear area, a saturation area and an approximate constant area, and different piecewise linear function fittings are used to reduce the hardware complexity, and the inference process is only performed on the hardware, using the adder and shifter implementation.
Performance Benchmarking Methodologies
Performance benchmarking for sigmoid function implementations requires systematic methodologies to ensure accurate and meaningful comparisons. When evaluating numerically stable sigmoid implementations, benchmarking should focus on both computational efficiency and numerical accuracy across diverse input ranges.
A comprehensive benchmarking framework begins with establishing baseline implementations, including the naive sigmoid formula, standard library implementations, and proposed stable alternatives. These implementations should be tested against identical input distributions, particularly focusing on extreme values where numerical instability typically manifests.
Execution time measurement represents a critical benchmarking dimension. Modern benchmarking tools like Google Benchmark for C++ or timeit in Python should be employed with statistical rigor, collecting multiple samples to account for system variability. Measurements should include both average execution time and distribution characteristics to identify performance consistency across repeated executions.
Memory consumption analysis forms another essential benchmarking component, particularly relevant for resource-constrained environments like mobile or embedded deep learning applications. Profiling tools should track both peak memory usage and allocation patterns during function execution.
Numerical accuracy testing requires comparing function outputs against high-precision reference implementations across strategically selected input ranges. Special attention must be paid to edge cases: extremely large positive/negative inputs, values near zero, and gradients across these regions. Statistical measures like Mean Absolute Error (MAE) and Maximum Error should be calculated to quantify deviation from reference values.
Hardware-specific performance characteristics demand evaluation across different computing architectures. Benchmarks should examine how implementations perform on CPUs with different instruction set architectures, GPUs, and specialized AI accelerators, as vectorization and parallelization opportunities vary significantly across platforms.
Finally, integration testing within actual deep learning frameworks provides the most realistic performance assessment. Implementations should be benchmarked within training loops of representative neural network architectures, measuring both per-iteration time impact and effects on convergence behavior. This reveals whether theoretical performance advantages translate to meaningful improvements in real-world deep learning workloads.
A comprehensive benchmarking framework begins with establishing baseline implementations, including the naive sigmoid formula, standard library implementations, and proposed stable alternatives. These implementations should be tested against identical input distributions, particularly focusing on extreme values where numerical instability typically manifests.
Execution time measurement represents a critical benchmarking dimension. Modern benchmarking tools like Google Benchmark for C++ or timeit in Python should be employed with statistical rigor, collecting multiple samples to account for system variability. Measurements should include both average execution time and distribution characteristics to identify performance consistency across repeated executions.
Memory consumption analysis forms another essential benchmarking component, particularly relevant for resource-constrained environments like mobile or embedded deep learning applications. Profiling tools should track both peak memory usage and allocation patterns during function execution.
Numerical accuracy testing requires comparing function outputs against high-precision reference implementations across strategically selected input ranges. Special attention must be paid to edge cases: extremely large positive/negative inputs, values near zero, and gradients across these regions. Statistical measures like Mean Absolute Error (MAE) and Maximum Error should be calculated to quantify deviation from reference values.
Hardware-specific performance characteristics demand evaluation across different computing architectures. Benchmarks should examine how implementations perform on CPUs with different instruction set architectures, GPUs, and specialized AI accelerators, as vectorization and parallelization opportunities vary significantly across platforms.
Finally, integration testing within actual deep learning frameworks provides the most realistic performance assessment. Implementations should be benchmarked within training loops of representative neural network architectures, measuring both per-iteration time impact and effects on convergence behavior. This reveals whether theoretical performance advantages translate to meaningful improvements in real-world deep learning workloads.
Hardware Acceleration Considerations
The implementation of numerically stable sigmoid functions in deep learning models requires careful consideration of hardware acceleration to achieve optimal performance. Modern deep learning frameworks leverage various hardware accelerators such as GPUs, TPUs, and specialized AI chips to speed up computation. When implementing sigmoid functions, the hardware architecture significantly impacts both performance and numerical stability. SIMD (Single Instruction Multiple Data) operations available on modern CPUs and GPUs can parallelize sigmoid calculations across multiple data points simultaneously, dramatically improving throughput for batch processing.
Vector processing units in GPUs are particularly well-suited for sigmoid function implementation as they can efficiently handle the exponential calculations required. However, different hardware accelerators implement exponential functions with varying precision levels. For instance, NVIDIA's GPU architecture provides specialized hardware units for fast approximation of exponential functions, which can be leveraged for sigmoid implementation but may introduce slight precision differences compared to CPU implementations.
Memory access patterns also play a crucial role in hardware-accelerated sigmoid implementations. Coalesced memory access on GPUs can significantly improve performance by reducing memory latency. When implementing sigmoid functions, arranging data in memory to maximize cache utilization and minimize bank conflicts becomes essential for high-performance implementations.
Quantization considerations become particularly important when deploying models on edge devices or specialized AI accelerators. Many hardware accelerators support reduced precision operations (INT8, FP16) that can significantly speed up sigmoid calculations but may exacerbate numerical stability issues. Implementing lookup table-based approaches for sigmoid functions can be particularly effective on hardware with limited floating-point capabilities, trading memory for computational efficiency.
Hardware-specific optimizations such as CUDA intrinsics for NVIDIA GPUs or OpenCL optimizations for AMD hardware can further enhance sigmoid function performance. Modern AI accelerators like Google's TPUs and Intel's Habana chips offer specialized activation function units that can compute sigmoid operations directly in hardware, eliminating the need for software implementations entirely for certain model architectures.
The choice between different sigmoid implementation strategies should consider the target hardware's characteristics, including available memory bandwidth, compute capabilities, and specialized function units. For instance, the log-sum-exp trick for numerical stability may have different performance implications on GPUs versus TPUs due to differences in how these architectures handle transcendental functions and memory access patterns.
Vector processing units in GPUs are particularly well-suited for sigmoid function implementation as they can efficiently handle the exponential calculations required. However, different hardware accelerators implement exponential functions with varying precision levels. For instance, NVIDIA's GPU architecture provides specialized hardware units for fast approximation of exponential functions, which can be leveraged for sigmoid implementation but may introduce slight precision differences compared to CPU implementations.
Memory access patterns also play a crucial role in hardware-accelerated sigmoid implementations. Coalesced memory access on GPUs can significantly improve performance by reducing memory latency. When implementing sigmoid functions, arranging data in memory to maximize cache utilization and minimize bank conflicts becomes essential for high-performance implementations.
Quantization considerations become particularly important when deploying models on edge devices or specialized AI accelerators. Many hardware accelerators support reduced precision operations (INT8, FP16) that can significantly speed up sigmoid calculations but may exacerbate numerical stability issues. Implementing lookup table-based approaches for sigmoid functions can be particularly effective on hardware with limited floating-point capabilities, trading memory for computational efficiency.
Hardware-specific optimizations such as CUDA intrinsics for NVIDIA GPUs or OpenCL optimizations for AMD hardware can further enhance sigmoid function performance. Modern AI accelerators like Google's TPUs and Intel's Habana chips offer specialized activation function units that can compute sigmoid operations directly in hardware, eliminating the need for software implementations entirely for certain model architectures.
The choice between different sigmoid implementation strategies should consider the target hardware's characteristics, including available memory bandwidth, compute capabilities, and specialized function units. For instance, the log-sum-exp trick for numerical stability may have different performance implications on GPUs versus TPUs due to differences in how these architectures handle transcendental functions and memory access patterns.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!