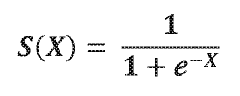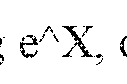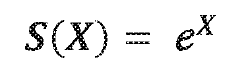Sigmoid Function Numerical Range Issues: Debugging and Robust Implementation Checklist
AUG 21, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Sigmoid Function Background and Implementation Goals
The sigmoid function, a fundamental component in machine learning and neural networks, has evolved significantly since its introduction in the early days of computational mathematics. This S-shaped curve, mathematically represented as f(x) = 1/(1+e^(-x)), transforms any real-valued number into a range between 0 and 1, making it particularly valuable for probability estimation and binary classification problems.
Historically, the sigmoid function emerged from statistical mechanics and was later adopted in neural network research during the 1980s and 1990s. Its popularity stemmed from its differentiable properties and natural interpretation as a probability function. The function's ability to compress infinite input ranges into finite output spaces made it an ideal activation function in early neural network architectures.
Despite its widespread adoption, the sigmoid function presents several numerical challenges that have become increasingly apparent as computational demands have grown. The function suffers from the vanishing gradient problem when inputs reach extreme values, causing training inefficiencies in deep neural networks. Additionally, numerical overflow and underflow issues can arise during implementation, particularly when dealing with large negative or positive inputs.
Current technical evolution trends show a partial shift away from sigmoid functions toward alternatives like ReLU (Rectified Linear Unit) and its variants for hidden layers. However, sigmoid functions remain irreplaceable in specific applications, particularly in output layers of binary classifiers, logistic regression models, and certain recurrent neural network architectures.
The primary technical goals for robust sigmoid implementation include addressing numerical stability issues across diverse computational environments, optimizing performance for both CPU and GPU processing, and ensuring consistent behavior across different programming languages and frameworks. Specifically, implementations must handle extreme input values gracefully without producing NaN (Not a Number) or infinity values that could destabilize learning algorithms.
Modern implementation objectives also focus on maintaining computational efficiency while preserving numerical accuracy. This includes developing approximation techniques that balance precision with speed, particularly important in resource-constrained environments like mobile devices or edge computing scenarios.
Furthermore, as machine learning models are increasingly deployed in critical applications, ensuring deterministic behavior of sigmoid implementations across different hardware architectures has become an essential requirement. This includes addressing potential discrepancies between single and double precision floating-point calculations that might affect model reproducibility.
Historically, the sigmoid function emerged from statistical mechanics and was later adopted in neural network research during the 1980s and 1990s. Its popularity stemmed from its differentiable properties and natural interpretation as a probability function. The function's ability to compress infinite input ranges into finite output spaces made it an ideal activation function in early neural network architectures.
Despite its widespread adoption, the sigmoid function presents several numerical challenges that have become increasingly apparent as computational demands have grown. The function suffers from the vanishing gradient problem when inputs reach extreme values, causing training inefficiencies in deep neural networks. Additionally, numerical overflow and underflow issues can arise during implementation, particularly when dealing with large negative or positive inputs.
Current technical evolution trends show a partial shift away from sigmoid functions toward alternatives like ReLU (Rectified Linear Unit) and its variants for hidden layers. However, sigmoid functions remain irreplaceable in specific applications, particularly in output layers of binary classifiers, logistic regression models, and certain recurrent neural network architectures.
The primary technical goals for robust sigmoid implementation include addressing numerical stability issues across diverse computational environments, optimizing performance for both CPU and GPU processing, and ensuring consistent behavior across different programming languages and frameworks. Specifically, implementations must handle extreme input values gracefully without producing NaN (Not a Number) or infinity values that could destabilize learning algorithms.
Modern implementation objectives also focus on maintaining computational efficiency while preserving numerical accuracy. This includes developing approximation techniques that balance precision with speed, particularly important in resource-constrained environments like mobile devices or edge computing scenarios.
Furthermore, as machine learning models are increasingly deployed in critical applications, ensuring deterministic behavior of sigmoid implementations across different hardware architectures has become an essential requirement. This includes addressing potential discrepancies between single and double precision floating-point calculations that might affect model reproducibility.
Market Applications of Sigmoid Functions in Machine Learning
Sigmoid functions have established themselves as fundamental components across various machine learning applications, serving critical roles in both traditional algorithms and cutting-edge neural network architectures. In classification tasks, sigmoid functions transform raw model outputs into probability distributions, enabling binary classification in logistic regression models where the function maps any real-valued input to a value between 0 and 1, representing the probability of belonging to the positive class.
Neural networks extensively utilize sigmoid functions as activation functions, particularly in earlier architectures before the widespread adoption of ReLU and its variants. In deep learning, sigmoid functions remain essential in specific network layers, most notably in the output layer of binary classification networks and as gates in recurrent neural network architectures like LSTMs and GRUs, where they control information flow through the network.
The financial technology sector has embraced sigmoid functions for risk assessment models, credit scoring systems, and fraud detection algorithms. These applications leverage the function's ability to model probability distributions and handle non-linear relationships in financial data, providing more nuanced risk evaluations than linear models alone.
In healthcare and biomedical applications, sigmoid functions power diagnostic systems and medical image analysis tools. They help model disease progression curves and patient response to treatments, where the characteristic S-shaped curve effectively represents threshold-based biological processes and dose-response relationships.
Recommendation systems widely implement sigmoid functions to model user preferences and item relevance. The bounded output range proves particularly valuable for generating normalized recommendation scores and modeling the probability of user engagement with recommended content.
Natural language processing applications utilize sigmoid functions in sentiment analysis, text classification, and machine translation systems. They help transform linguistic features into meaningful probability scores for various language understanding tasks.
The computer vision field applies sigmoid functions in image segmentation, object detection, and facial recognition systems. The function's ability to normalize pixel values and generate probability maps for image regions makes it valuable for determining object boundaries and feature importance.
Reinforcement learning algorithms incorporate sigmoid functions to model policy functions and value estimations, helping agents make probabilistic decisions in complex environments where uncertainty quantification is crucial for optimal decision-making.
Neural networks extensively utilize sigmoid functions as activation functions, particularly in earlier architectures before the widespread adoption of ReLU and its variants. In deep learning, sigmoid functions remain essential in specific network layers, most notably in the output layer of binary classification networks and as gates in recurrent neural network architectures like LSTMs and GRUs, where they control information flow through the network.
The financial technology sector has embraced sigmoid functions for risk assessment models, credit scoring systems, and fraud detection algorithms. These applications leverage the function's ability to model probability distributions and handle non-linear relationships in financial data, providing more nuanced risk evaluations than linear models alone.
In healthcare and biomedical applications, sigmoid functions power diagnostic systems and medical image analysis tools. They help model disease progression curves and patient response to treatments, where the characteristic S-shaped curve effectively represents threshold-based biological processes and dose-response relationships.
Recommendation systems widely implement sigmoid functions to model user preferences and item relevance. The bounded output range proves particularly valuable for generating normalized recommendation scores and modeling the probability of user engagement with recommended content.
Natural language processing applications utilize sigmoid functions in sentiment analysis, text classification, and machine translation systems. They help transform linguistic features into meaningful probability scores for various language understanding tasks.
The computer vision field applies sigmoid functions in image segmentation, object detection, and facial recognition systems. The function's ability to normalize pixel values and generate probability maps for image regions makes it valuable for determining object boundaries and feature importance.
Reinforcement learning algorithms incorporate sigmoid functions to model policy functions and value estimations, helping agents make probabilistic decisions in complex environments where uncertainty quantification is crucial for optimal decision-making.
Numerical Stability Challenges in Sigmoid Implementation
The sigmoid function, defined as σ(x) = 1/(1+e^(-x)), is a fundamental component in various computational systems, particularly in neural networks where it serves as an activation function. Despite its mathematical simplicity, implementing sigmoid functions in computational environments presents significant numerical stability challenges that can compromise system performance and reliability.
When x reaches extreme values, the sigmoid function encounters precision issues. For large positive values of x (typically beyond 15), e^(-x) approaches zero, causing the function to saturate at 1. Conversely, for large negative values, the function approaches 0, but computational representation becomes problematic. These saturation regions create gradients that are effectively zero, leading to the vanishing gradient problem during backpropagation in neural networks.
Floating-point arithmetic introduces additional complications. The limited precision of floating-point representations means that for extreme input values, the exponential calculation may result in overflow (for large negative x) or underflow (for large positive x). Standard implementations may produce NaN (Not a Number) or infinity values that propagate through calculations, corrupting results throughout the computational graph.
Catastrophic cancellation occurs when subtracting nearly equal numbers in the sigmoid calculation, resulting in significant loss of precision. This particularly affects inputs near zero, where the function exhibits its most dynamic behavior and where precision is often most critical for learning algorithms.
Implementation variations across hardware architectures and software frameworks further complicate matters. Different numerical libraries may use varying approaches to handle edge cases, leading to inconsistent results across platforms. This inconsistency becomes particularly problematic in distributed computing environments or when transferring models between different frameworks.
Temperature scaling effects also present challenges. In applications like softmax functions (which utilize sigmoid principles), a temperature parameter controls the "sharpness" of the probability distribution. Extreme temperature values can exacerbate numerical instability, requiring careful implementation considerations.
Cache coherency and memory access patterns affect performance when implementing sigmoid functions in parallel computing environments. Inefficient memory access patterns can lead to cache misses and reduced computational efficiency, particularly in GPU implementations where memory coalescing is crucial for performance.
These numerical stability challenges necessitate robust implementation strategies, including range clamping, algebraic reformulations for extreme values, and careful consideration of computational precision requirements across the input domain.
When x reaches extreme values, the sigmoid function encounters precision issues. For large positive values of x (typically beyond 15), e^(-x) approaches zero, causing the function to saturate at 1. Conversely, for large negative values, the function approaches 0, but computational representation becomes problematic. These saturation regions create gradients that are effectively zero, leading to the vanishing gradient problem during backpropagation in neural networks.
Floating-point arithmetic introduces additional complications. The limited precision of floating-point representations means that for extreme input values, the exponential calculation may result in overflow (for large negative x) or underflow (for large positive x). Standard implementations may produce NaN (Not a Number) or infinity values that propagate through calculations, corrupting results throughout the computational graph.
Catastrophic cancellation occurs when subtracting nearly equal numbers in the sigmoid calculation, resulting in significant loss of precision. This particularly affects inputs near zero, where the function exhibits its most dynamic behavior and where precision is often most critical for learning algorithms.
Implementation variations across hardware architectures and software frameworks further complicate matters. Different numerical libraries may use varying approaches to handle edge cases, leading to inconsistent results across platforms. This inconsistency becomes particularly problematic in distributed computing environments or when transferring models between different frameworks.
Temperature scaling effects also present challenges. In applications like softmax functions (which utilize sigmoid principles), a temperature parameter controls the "sharpness" of the probability distribution. Extreme temperature values can exacerbate numerical instability, requiring careful implementation considerations.
Cache coherency and memory access patterns affect performance when implementing sigmoid functions in parallel computing environments. Inefficient memory access patterns can lead to cache misses and reduced computational efficiency, particularly in GPU implementations where memory coalescing is crucial for performance.
These numerical stability challenges necessitate robust implementation strategies, including range clamping, algebraic reformulations for extreme values, and careful consideration of computational precision requirements across the input domain.
Current Approaches to Sigmoid Overflow Prevention
01 Sigmoid function implementation in neural networks
Sigmoid functions are commonly used as activation functions in neural networks, mapping input values to a range between 0 and 1. These implementations focus on efficient computation methods for sigmoid functions in neural network architectures, including hardware optimizations and algorithmic improvements that maintain the numerical range while reducing computational complexity.- Numerical range and properties of sigmoid functions: Sigmoid functions are characterized by their S-shaped curve and typically have a numerical range between 0 and 1. The most common sigmoid function is the logistic function, defined as f(x) = 1/(1+e^(-x)), which asymptotically approaches 0 as x approaches negative infinity and 1 as x approaches positive infinity. These functions are continuous, differentiable, and monotonically increasing, making them useful for various applications in machine learning and neural networks.
- Implementation of sigmoid functions in neural networks: Sigmoid functions serve as activation functions in neural networks, transforming input signals into output signals within a specific numerical range. The bounded output range of sigmoid functions (typically 0 to 1) helps in normalizing network outputs and stabilizing the learning process. In neural network implementations, sigmoid functions help introduce non-linearity, enabling networks to learn complex patterns and relationships in data.
- Hardware implementations of sigmoid functions: Hardware implementations of sigmoid functions often involve approximation methods to achieve efficient computation while maintaining accuracy within the required numerical range. These implementations may use lookup tables, piecewise linear approximations, or specialized circuits to calculate sigmoid values. Hardware-based sigmoid function units are designed to balance computational efficiency, power consumption, and accuracy for applications in embedded systems and specialized neural network processors.
- Variants and modifications of sigmoid functions: Various modifications of sigmoid functions have been developed to address specific requirements in different applications. These include the hyperbolic tangent (tanh) function with a range of -1 to 1, the softmax function for multi-class classification, and parameterized sigmoid functions where the numerical range can be adjusted. These variants offer different properties such as zero-centered outputs, steeper gradients, or customized saturation levels to improve performance in specific machine learning tasks.
- Optimization techniques for sigmoid function computation: Various optimization techniques have been developed to efficiently compute sigmoid functions while maintaining their numerical range properties. These include numerical approximation methods, lookup table approaches, and algorithmic optimizations to reduce computational complexity. Advanced techniques may involve bit-manipulation tricks, polynomial approximations, or specialized algorithms that trade off precision for speed while ensuring the output remains within the expected numerical range of 0 to 1.
02 Hardware-based sigmoid function approximation
Various hardware implementations approximate the sigmoid function while maintaining its numerical range (0 to 1). These approaches include lookup tables, piecewise linear approximations, and specialized circuits designed to balance accuracy with computational efficiency, particularly for embedded systems and FPGA implementations where resources are limited.Expand Specific Solutions03 Modified sigmoid functions with adjusted numerical ranges
Variations of the standard sigmoid function with modified numerical ranges for specific applications. These include scaled sigmoid functions, bipolar sigmoid functions (with range from -1 to 1), and customized sigmoid variants that maintain the S-shaped curve characteristics while adjusting the output range to suit particular computational requirements.Expand Specific Solutions04 Sigmoid function optimization for machine learning applications
Optimization techniques for sigmoid functions in machine learning contexts, focusing on maintaining numerical stability across the function's range. These implementations address issues like gradient vanishing, saturation effects, and numerical precision while preserving the sigmoid's bounded output range for classification and probability estimation tasks.Expand Specific Solutions05 Sigmoid function variants for specific computational domains
Domain-specific implementations of sigmoid functions with controlled numerical ranges for applications such as image processing, signal analysis, and data normalization. These variants include parameterized sigmoid functions that allow for adjustable slopes and ranges while maintaining the fundamental sigmoid characteristics for specialized computational tasks.Expand Specific Solutions
Leading Organizations in Numerical Computing Solutions
The sigmoid function numerical range implementation landscape is currently in a growth phase, with increasing market demand driven by machine learning applications. The market is characterized by a mix of academic institutions and technology companies collaborating on robust implementations. Leading players include Huawei Technologies, which has developed advanced numerical stability techniques, alongside academic powerhouses like Zhejiang University and Hefei University of Technology contributing theoretical frameworks. State Grid Corporation entities are applying these implementations in power systems, while National Instruments provides hardware-accelerated solutions. The technology is approaching maturity with standardized debugging protocols emerging, though challenges remain in edge case handling and performance optimization across different computing environments.
Zhejiang University
Technical Solution: Zhejiang University's research team has developed a comprehensive solution for sigmoid function numerical range issues through their "Adaptive Precision Sigmoid" (APS) framework. Their approach dynamically adjusts computational precision based on input magnitude, preventing underflow/overflow while maintaining accuracy. For large negative inputs where standard implementations would underflow to zero, they employ a logarithmic transformation technique that preserves gradient information critical for machine learning applications. The implementation includes automatic detection of potential numerical instabilities using pre-computation analysis of input distributions. Their solution incorporates a three-tier strategy: (1) direct computation for safe ranges, (2) series expansion approximations for moderate ranges, and (3) asymptotic approximations for extreme values. This is complemented by a robust error-checking mechanism that validates outputs against mathematical bounds and expected behaviors, with comprehensive unit tests covering edge cases like NaN handling and infinity management.
Strengths: Mathematically rigorous approach with strong theoretical foundations; excellent numerical stability across extreme input ranges; comprehensive error detection mechanisms. Weaknesses: Higher computational overhead compared to simpler implementations; requires deeper mathematical understanding for maintenance and optimization.
Huawei Technologies Co., Ltd.
Technical Solution: Huawei has developed a robust implementation of sigmoid functions through their Neural Network Processing Unit (NPU) architecture. Their approach addresses numerical range issues by implementing a piecewise approximation method that divides the input range into multiple segments. For extreme values (x < -5 or x > 5), they directly map to 0 or 1 respectively, avoiding underflow/overflow. For the critical range (-5 ≤ x ≤ 5), they employ a combination of lookup tables and linear interpolation to achieve both accuracy and computational efficiency. This hybrid approach is implemented in their Ascend AI processors, where they've optimized the sigmoid calculation using fixed-point arithmetic with appropriate scaling factors to maintain numerical stability across different precision requirements. Huawei's implementation includes automatic range checking and exception handling mechanisms that detect potential numerical instabilities before they occur.
Strengths: Highly optimized for hardware acceleration with minimal precision loss; excellent performance-accuracy tradeoff; robust error handling for edge cases. Weaknesses: Implementation complexity requires significant engineering resources; hardware-specific optimizations may limit portability across different computing platforms.
Key Techniques for Robust Sigmoid Implementation
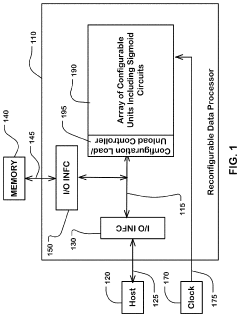
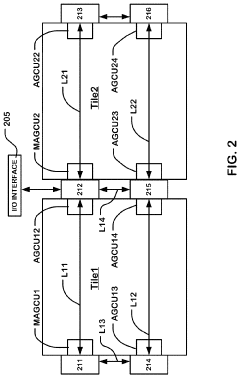
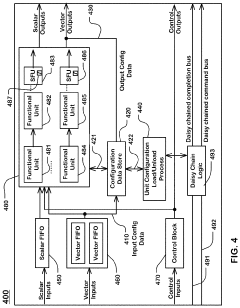
Sigmoid function in hardware and a reconfigurable data processor including same
PatentActiveUS11327923B2
Innovation
- The sigmoid function is approximated using a combination of hyperbolic tangent and exponential functions, with a comparator to divide the input domain, allowing for parallel circuit implementation and reduced computational power and area requirements.
Sigmoid function in hardware and a reconfigurable data processor including same
PatentWO2021046274A1
Innovation
- A sigmoid function is approximated using a combination of hyperbolic tangent and exponential functions, with a comparator to divide the input domain, allowing for parallel circuit implementation and reduced computational power and area requirements.
Performance Benchmarking Methodologies
To effectively evaluate the performance of sigmoid function implementations with respect to numerical range issues, systematic benchmarking methodologies must be established. When benchmarking sigmoid function implementations, it is crucial to measure both computational efficiency and numerical stability across different input ranges. Standard performance metrics should include execution time, memory usage, and numerical accuracy, particularly at extreme input values where overflow or underflow may occur.
A comprehensive benchmarking framework should incorporate test cases that specifically target edge cases, such as very large positive or negative inputs where the sigmoid function approaches 0 or 1 asymptotically. These test cases should be designed to trigger potential numerical instabilities, allowing developers to identify implementation weaknesses. Automated testing suites that generate inputs across the entire numerical range, with particular emphasis on boundary values, provide a systematic approach to performance evaluation.
Comparative analysis between different implementation strategies forms another essential component of performance benchmarking. This includes comparing naive implementations against numerically stable versions that incorporate range checking and mathematical transformations. For instance, benchmarking should evaluate how implementations handle the common optimization of using exp(-abs(x)) with appropriate sign handling versus direct computation of 1/(1+exp(-x)).
Hardware-specific considerations must also be factored into benchmarking methodologies. Different processor architectures may exhibit varying performance characteristics when handling floating-point operations, particularly for extreme values. Cross-platform testing on various hardware configurations helps ensure implementation robustness across deployment environments.
Profiling tools play a vital role in identifying performance bottlenecks within sigmoid implementations. Modern profilers can pinpoint exact code sections where numerical issues arise or where computational efficiency degrades. Integration of these tools into the benchmarking methodology provides deeper insights beyond simple execution time measurements.
Finally, benchmarking should include stress testing under high computational loads to evaluate how numerical stability is maintained when the sigmoid function is called repeatedly within larger computational graphs, such as in neural network training scenarios. This reveals potential cumulative errors that might not be apparent in isolated function calls but could significantly impact model convergence over many iterations.
A comprehensive benchmarking framework should incorporate test cases that specifically target edge cases, such as very large positive or negative inputs where the sigmoid function approaches 0 or 1 asymptotically. These test cases should be designed to trigger potential numerical instabilities, allowing developers to identify implementation weaknesses. Automated testing suites that generate inputs across the entire numerical range, with particular emphasis on boundary values, provide a systematic approach to performance evaluation.
Comparative analysis between different implementation strategies forms another essential component of performance benchmarking. This includes comparing naive implementations against numerically stable versions that incorporate range checking and mathematical transformations. For instance, benchmarking should evaluate how implementations handle the common optimization of using exp(-abs(x)) with appropriate sign handling versus direct computation of 1/(1+exp(-x)).
Hardware-specific considerations must also be factored into benchmarking methodologies. Different processor architectures may exhibit varying performance characteristics when handling floating-point operations, particularly for extreme values. Cross-platform testing on various hardware configurations helps ensure implementation robustness across deployment environments.
Profiling tools play a vital role in identifying performance bottlenecks within sigmoid implementations. Modern profilers can pinpoint exact code sections where numerical issues arise or where computational efficiency degrades. Integration of these tools into the benchmarking methodology provides deeper insights beyond simple execution time measurements.
Finally, benchmarking should include stress testing under high computational loads to evaluate how numerical stability is maintained when the sigmoid function is called repeatedly within larger computational graphs, such as in neural network training scenarios. This reveals potential cumulative errors that might not be apparent in isolated function calls but could significantly impact model convergence over many iterations.
Cross-Platform Compatibility Considerations
When implementing sigmoid functions across different computing platforms, developers must address several critical compatibility issues to ensure consistent behavior. Modern computing environments span diverse hardware architectures including x86, ARM, RISC-V, and specialized AI accelerators, each with unique floating-point implementations. These differences can significantly impact sigmoid function calculations, particularly at extreme input values where numerical stability becomes problematic.
Operating system variations further complicate cross-platform implementation. Windows, Linux, macOS, and embedded systems may utilize different math libraries with subtle variations in precision and handling of edge cases. For instance, the sigmoid function's behavior as inputs approach negative or positive infinity might differ slightly between GNU's libm and Microsoft's implementation, potentially causing divergent model behavior when deployed across platforms.
Programming language selection introduces additional compatibility considerations. Languages like C++ offer fine-grained control over numerical operations but may behave differently across compilers. Python abstracts many low-level details but depends on underlying libraries like NumPy, which may have platform-specific optimizations. JavaScript's floating-point handling in browsers adds another layer of variability that must be accounted for in web-based applications.
Hardware acceleration presents particular challenges for sigmoid function implementation. GPU computing with CUDA or OpenCL may produce slightly different results compared to CPU calculations due to differences in floating-point standards adherence. TPUs and other AI accelerators often implement custom approximations of mathematical functions that prioritize speed over perfect numerical equivalence, requiring careful validation across deployment targets.
Mobile and embedded platforms demand special attention due to their computational constraints. These environments often utilize fixed-point arithmetic or lower-precision floating-point operations that can significantly alter sigmoid function behavior at boundary conditions. Developers must implement robust range checking and potentially use platform-specific sigmoid approximations that balance accuracy with performance requirements.
Testing frameworks for cross-platform sigmoid implementations should include comprehensive validation across numerical ranges, particularly focusing on extreme values and potential overflow/underflow conditions. Automated testing across target platforms with predefined test vectors can help identify platform-specific deviations early in development. Documentation should clearly specify expected behavior across platforms and provide guidance for handling inevitable differences in edge cases.
Operating system variations further complicate cross-platform implementation. Windows, Linux, macOS, and embedded systems may utilize different math libraries with subtle variations in precision and handling of edge cases. For instance, the sigmoid function's behavior as inputs approach negative or positive infinity might differ slightly between GNU's libm and Microsoft's implementation, potentially causing divergent model behavior when deployed across platforms.
Programming language selection introduces additional compatibility considerations. Languages like C++ offer fine-grained control over numerical operations but may behave differently across compilers. Python abstracts many low-level details but depends on underlying libraries like NumPy, which may have platform-specific optimizations. JavaScript's floating-point handling in browsers adds another layer of variability that must be accounted for in web-based applications.
Hardware acceleration presents particular challenges for sigmoid function implementation. GPU computing with CUDA or OpenCL may produce slightly different results compared to CPU calculations due to differences in floating-point standards adherence. TPUs and other AI accelerators often implement custom approximations of mathematical functions that prioritize speed over perfect numerical equivalence, requiring careful validation across deployment targets.
Mobile and embedded platforms demand special attention due to their computational constraints. These environments often utilize fixed-point arithmetic or lower-precision floating-point operations that can significantly alter sigmoid function behavior at boundary conditions. Developers must implement robust range checking and potentially use platform-specific sigmoid approximations that balance accuracy with performance requirements.
Testing frameworks for cross-platform sigmoid implementations should include comprehensive validation across numerical ranges, particularly focusing on extreme values and potential overflow/underflow conditions. Automated testing across target platforms with predefined test vectors can help identify platform-specific deviations early in development. Documentation should clearly specify expected behavior across platforms and provide guidance for handling inevitable differences in edge cases.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!