How to Model Laminar Flow for Accurate Predictions?
JUL 10, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Laminar Flow Modeling Background and Objectives
Laminar flow modeling has been a cornerstone in fluid dynamics research and engineering applications for decades. This predictive technique is crucial for understanding and optimizing fluid behavior in various systems, from microfluidic devices to large-scale industrial processes. The evolution of laminar flow modeling has been closely tied to advancements in computational power and numerical methods, enabling increasingly accurate and complex simulations.
The primary objective of laminar flow modeling is to provide precise predictions of fluid behavior under specific conditions where viscous forces dominate over inertial forces. This is typically characterized by low Reynolds numbers, where fluid particles move in parallel layers without lateral mixing. Accurate modeling of laminar flow is essential for a wide range of applications, including biomedical engineering, chemical processing, and aerospace design.
Historically, laminar flow modeling began with analytical solutions for simple geometries and idealized conditions. The Navier-Stokes equations, formulated in the 19th century, provided the mathematical foundation for describing fluid motion. However, solving these equations for complex real-world scenarios remained a significant challenge until the advent of computational fluid dynamics (CFD) in the mid-20th century.
As computational capabilities have grown, so too has the sophistication of laminar flow models. Modern approaches incorporate multi-physics simulations, coupling fluid dynamics with heat transfer, chemical reactions, and other phenomena. This holistic modeling approach aims to capture the intricate interplay between various physical processes in laminar flow systems.
The current technological landscape demands ever more precise predictions of laminar flow behavior. Industries such as microfluidics, where precise control of small fluid volumes is critical, rely heavily on accurate laminar flow models. In the biomedical field, understanding laminar flow is crucial for designing drug delivery systems and artificial organs. Aerospace engineers utilize laminar flow models to optimize wing designs and reduce drag, contributing to more fuel-efficient aircraft.
Looking forward, the goals of laminar flow modeling are multifaceted. Researchers and engineers strive to develop models that can handle increasingly complex geometries and multi-phase flows while maintaining computational efficiency. There is also a push towards real-time simulation capabilities, enabling on-the-fly adjustments in industrial processes and medical applications.
Another key objective is the integration of machine learning techniques with traditional CFD approaches. This hybrid modeling strategy aims to enhance prediction accuracy while reducing computational costs, potentially revolutionizing how we approach laminar flow simulations in the future.
The primary objective of laminar flow modeling is to provide precise predictions of fluid behavior under specific conditions where viscous forces dominate over inertial forces. This is typically characterized by low Reynolds numbers, where fluid particles move in parallel layers without lateral mixing. Accurate modeling of laminar flow is essential for a wide range of applications, including biomedical engineering, chemical processing, and aerospace design.
Historically, laminar flow modeling began with analytical solutions for simple geometries and idealized conditions. The Navier-Stokes equations, formulated in the 19th century, provided the mathematical foundation for describing fluid motion. However, solving these equations for complex real-world scenarios remained a significant challenge until the advent of computational fluid dynamics (CFD) in the mid-20th century.
As computational capabilities have grown, so too has the sophistication of laminar flow models. Modern approaches incorporate multi-physics simulations, coupling fluid dynamics with heat transfer, chemical reactions, and other phenomena. This holistic modeling approach aims to capture the intricate interplay between various physical processes in laminar flow systems.
The current technological landscape demands ever more precise predictions of laminar flow behavior. Industries such as microfluidics, where precise control of small fluid volumes is critical, rely heavily on accurate laminar flow models. In the biomedical field, understanding laminar flow is crucial for designing drug delivery systems and artificial organs. Aerospace engineers utilize laminar flow models to optimize wing designs and reduce drag, contributing to more fuel-efficient aircraft.
Looking forward, the goals of laminar flow modeling are multifaceted. Researchers and engineers strive to develop models that can handle increasingly complex geometries and multi-phase flows while maintaining computational efficiency. There is also a push towards real-time simulation capabilities, enabling on-the-fly adjustments in industrial processes and medical applications.
Another key objective is the integration of machine learning techniques with traditional CFD approaches. This hybrid modeling strategy aims to enhance prediction accuracy while reducing computational costs, potentially revolutionizing how we approach laminar flow simulations in the future.
Industrial Applications and Market Demand
Laminar flow modeling has become increasingly crucial in various industrial sectors, driving significant market demand for accurate prediction tools. The automotive industry heavily relies on laminar flow modeling for aerodynamic design optimization, enhancing fuel efficiency, and reducing emissions. Automotive manufacturers utilize computational fluid dynamics (CFD) software to simulate laminar flow around vehicle bodies, resulting in improved performance and reduced development costs.
In the aerospace sector, laminar flow modeling plays a vital role in aircraft design, particularly for wings and fuselage components. By accurately predicting laminar flow behavior, engineers can optimize wing shapes and surface treatments to minimize drag and improve overall flight efficiency. This application has led to the development of advanced laminar flow control technologies, which are now being implemented in next-generation aircraft designs.
The renewable energy industry, especially wind power, has seen a surge in demand for laminar flow modeling. Wind turbine manufacturers use these models to optimize blade designs, maximizing energy capture while minimizing structural loads. Accurate laminar flow predictions enable the development of more efficient and durable wind turbines, contributing to the growth of sustainable energy production.
In the biomedical field, laminar flow modeling has found applications in the design of medical devices and drug delivery systems. For instance, accurate predictions of laminar flow in blood vessels and artificial organs are essential for developing effective cardiovascular implants and improving drug delivery mechanisms. This has led to increased collaboration between biomedical engineers and fluid dynamics specialists.
The chemical processing industry relies on laminar flow modeling for optimizing reactor designs and improving mixing processes. Accurate predictions of laminar flow behavior in various chemical reactors enable engineers to enhance reaction efficiency, reduce energy consumption, and improve product quality. This application has driven the development of specialized CFD software tailored for chemical engineering applications.
The HVAC (Heating, Ventilation, and Air Conditioning) industry has also seen growing demand for laminar flow modeling. Engineers use these models to design more efficient air distribution systems, optimize heat exchangers, and improve indoor air quality. The increasing focus on energy-efficient buildings and sustainable design has further amplified the importance of accurate laminar flow predictions in this sector.
As industries continue to prioritize efficiency, sustainability, and innovation, the market demand for advanced laminar flow modeling tools is expected to grow. This trend is driving investments in research and development of more sophisticated CFD software, machine learning-enhanced prediction algorithms, and high-performance computing solutions to meet the evolving needs of various industrial applications.
In the aerospace sector, laminar flow modeling plays a vital role in aircraft design, particularly for wings and fuselage components. By accurately predicting laminar flow behavior, engineers can optimize wing shapes and surface treatments to minimize drag and improve overall flight efficiency. This application has led to the development of advanced laminar flow control technologies, which are now being implemented in next-generation aircraft designs.
The renewable energy industry, especially wind power, has seen a surge in demand for laminar flow modeling. Wind turbine manufacturers use these models to optimize blade designs, maximizing energy capture while minimizing structural loads. Accurate laminar flow predictions enable the development of more efficient and durable wind turbines, contributing to the growth of sustainable energy production.
In the biomedical field, laminar flow modeling has found applications in the design of medical devices and drug delivery systems. For instance, accurate predictions of laminar flow in blood vessels and artificial organs are essential for developing effective cardiovascular implants and improving drug delivery mechanisms. This has led to increased collaboration between biomedical engineers and fluid dynamics specialists.
The chemical processing industry relies on laminar flow modeling for optimizing reactor designs and improving mixing processes. Accurate predictions of laminar flow behavior in various chemical reactors enable engineers to enhance reaction efficiency, reduce energy consumption, and improve product quality. This application has driven the development of specialized CFD software tailored for chemical engineering applications.
The HVAC (Heating, Ventilation, and Air Conditioning) industry has also seen growing demand for laminar flow modeling. Engineers use these models to design more efficient air distribution systems, optimize heat exchangers, and improve indoor air quality. The increasing focus on energy-efficient buildings and sustainable design has further amplified the importance of accurate laminar flow predictions in this sector.
As industries continue to prioritize efficiency, sustainability, and innovation, the market demand for advanced laminar flow modeling tools is expected to grow. This trend is driving investments in research and development of more sophisticated CFD software, machine learning-enhanced prediction algorithms, and high-performance computing solutions to meet the evolving needs of various industrial applications.
Current Challenges in Laminar Flow Prediction
Despite significant advancements in computational fluid dynamics (CFD), accurately predicting laminar flow remains a challenging task. One of the primary difficulties lies in capturing the complex interactions between fluid particles at the microscopic level, which collectively influence the macroscopic behavior of the flow. The inherent sensitivity of laminar flow to initial conditions and boundary geometries further complicates the modeling process.
A major challenge in laminar flow prediction is the accurate representation of viscous effects, particularly in regions close to solid boundaries. The no-slip condition at walls creates steep velocity gradients, requiring high-resolution meshes to resolve the flow field adequately. This often leads to increased computational costs and potential numerical instabilities, especially for complex geometries or long simulation times.
Another significant hurdle is the treatment of multi-phase flows and interfaces. When modeling laminar flow involving multiple fluids or phases, accurately capturing the interface dynamics and associated surface tension effects becomes crucial. Current numerical methods often struggle to maintain sharp interfaces and conserve mass across phase boundaries, leading to inaccuracies in flow prediction.
The presence of heat transfer and temperature-dependent fluid properties introduces additional complexities to laminar flow modeling. Accurately coupling the momentum and energy equations while accounting for temperature-induced variations in viscosity and density remains a challenging task. This is particularly evident in natural convection problems or flows with significant temperature gradients.
Furthermore, the transition from laminar to turbulent flow poses a significant challenge in flow prediction. Accurately determining the onset of instabilities and capturing the early stages of transition requires sophisticated models and high-resolution simulations. The lack of a universal criterion for predicting transition points adds to the uncertainty in flow modeling.
Lastly, the validation of laminar flow models against experimental data presents its own set of challenges. Obtaining high-quality experimental measurements for complex laminar flows, especially at small scales or in confined geometries, can be difficult. This limits the ability to rigorously validate and improve numerical models, potentially leading to discrepancies between simulations and real-world observations.
Addressing these challenges requires ongoing research and development in numerical methods, mesh generation techniques, and physical modeling approaches. Advances in high-performance computing and machine learning algorithms may offer new avenues for improving the accuracy and efficiency of laminar flow predictions in the future.
A major challenge in laminar flow prediction is the accurate representation of viscous effects, particularly in regions close to solid boundaries. The no-slip condition at walls creates steep velocity gradients, requiring high-resolution meshes to resolve the flow field adequately. This often leads to increased computational costs and potential numerical instabilities, especially for complex geometries or long simulation times.
Another significant hurdle is the treatment of multi-phase flows and interfaces. When modeling laminar flow involving multiple fluids or phases, accurately capturing the interface dynamics and associated surface tension effects becomes crucial. Current numerical methods often struggle to maintain sharp interfaces and conserve mass across phase boundaries, leading to inaccuracies in flow prediction.
The presence of heat transfer and temperature-dependent fluid properties introduces additional complexities to laminar flow modeling. Accurately coupling the momentum and energy equations while accounting for temperature-induced variations in viscosity and density remains a challenging task. This is particularly evident in natural convection problems or flows with significant temperature gradients.
Furthermore, the transition from laminar to turbulent flow poses a significant challenge in flow prediction. Accurately determining the onset of instabilities and capturing the early stages of transition requires sophisticated models and high-resolution simulations. The lack of a universal criterion for predicting transition points adds to the uncertainty in flow modeling.
Lastly, the validation of laminar flow models against experimental data presents its own set of challenges. Obtaining high-quality experimental measurements for complex laminar flows, especially at small scales or in confined geometries, can be difficult. This limits the ability to rigorously validate and improve numerical models, potentially leading to discrepancies between simulations and real-world observations.
Addressing these challenges requires ongoing research and development in numerical methods, mesh generation techniques, and physical modeling approaches. Advances in high-performance computing and machine learning algorithms may offer new avenues for improving the accuracy and efficiency of laminar flow predictions in the future.
State-of-the-Art Laminar Flow Modeling Techniques
01 Laminar flow control in fluid systems
Techniques for controlling and maintaining laminar flow in fluid systems to improve accuracy and precision. This includes methods for reducing turbulence, optimizing flow channels, and using specialized components to ensure smooth, predictable fluid movement.- Laminar flow control in fluid systems: Techniques for controlling and maintaining laminar flow in fluid systems to improve accuracy and efficiency. This includes methods for reducing turbulence, optimizing flow channels, and using specialized components to ensure smooth, predictable fluid movement.
- Measurement and analysis of laminar flow: Advanced methods for measuring and analyzing laminar flow characteristics, including the use of sensors, imaging techniques, and data processing algorithms. These approaches enable precise quantification of flow parameters and detection of deviations from ideal laminar conditions.
- Laminar flow in medical and laboratory applications: Specialized laminar flow systems designed for medical and laboratory environments, focusing on maintaining sterile conditions, precise sample handling, and accurate diagnostic procedures. These systems often incorporate advanced filtration and contamination control mechanisms.
- Enhancing laminar flow in industrial processes: Innovations in industrial equipment and processes to promote laminar flow, improving manufacturing precision, product quality, and energy efficiency. This includes advancements in mixing, coating, and material handling operations that rely on controlled fluid dynamics.
- Computational modeling and simulation of laminar flow: Development of sophisticated computational models and simulation techniques to predict and optimize laminar flow behavior in various systems. These tools enable engineers to design more efficient flow systems and anticipate potential issues before physical implementation.
02 Laminar flow measurement and analysis
Advanced methods for measuring and analyzing laminar flow characteristics, including the use of sensors, imaging techniques, and data processing algorithms to accurately quantify flow parameters and detect deviations from ideal laminar conditions.Expand Specific Solutions03 Laminar flow in microfluidic devices
Specialized approaches for achieving and maintaining laminar flow in microfluidic devices, focusing on miniaturized systems where precise fluid control is critical for accurate results in applications such as lab-on-a-chip technologies and microanalysis systems.Expand Specific Solutions04 Laminar flow nozzles and spray systems
Design and optimization of nozzles and spray systems that utilize laminar flow principles to enhance accuracy and uniformity in fluid dispensing applications, such as coating processes, 3D printing, and precision manufacturing.Expand Specific Solutions05 Laminar flow in heat exchange and cooling systems
Utilization of laminar flow principles in heat exchange and cooling systems to improve thermal management efficiency and accuracy. This includes optimizing flow patterns in heat sinks, radiators, and other thermal management devices to enhance heat transfer and temperature control.Expand Specific Solutions
Key Players in Fluid Dynamics Simulation
The laminar flow modeling market is in a mature stage, with established players and well-developed techniques. The global market size for computational fluid dynamics (CFD) software, which includes laminar flow modeling, is estimated to reach $2.5 billion by 2025. Technological advancements in high-performance computing and machine learning are driving innovation in this field. Key players like Schlumberger Technologies, Shell USA, and Dassault Systèmes Americas Corp. are investing in research and development to improve the accuracy and efficiency of laminar flow predictions. Academic institutions such as Hohai University and Northwestern Polytechnical University are also contributing to the advancement of laminar flow modeling techniques through collaborative research projects with industry partners.
Schlumberger Technologies, Inc.
Technical Solution: Schlumberger has developed advanced laminar flow modeling techniques for accurate predictions in oil and gas exploration. Their approach combines computational fluid dynamics (CFD) with machine learning algorithms to enhance the accuracy of flow simulations. The company utilizes high-resolution 3D reservoir models and incorporates real-time data from downhole sensors to calibrate and refine their laminar flow predictions[1]. Schlumberger's models account for complex geological structures, fluid properties, and multiphase flow behaviors, allowing for more precise estimations of reservoir performance and production rates[2]. Their technology also integrates with reservoir characterization tools to provide a comprehensive understanding of fluid dynamics in porous media[3].
Strengths: Extensive industry experience, access to vast amounts of field data, and integration with other reservoir management tools. Weaknesses: High computational requirements and potential limitations in unconventional reservoirs.
Shell-USA, Inc.
Technical Solution: Shell-USA has implemented a multi-scale approach to modeling laminar flow for accurate predictions in various applications, including pipeline transport and reservoir simulation. Their methodology combines pore-scale modeling with continuum-scale simulations to capture both microscopic and macroscopic flow behaviors[4]. Shell's models incorporate advanced numerical methods, such as lattice Boltzmann simulations, to accurately represent complex geometries and fluid-solid interactions[5]. The company has also developed proprietary algorithms to upscale pore-scale results to field-scale predictions, improving the overall accuracy of their laminar flow models. Shell's approach includes the integration of experimental data and field measurements to validate and refine their simulations, ensuring reliable predictions across different operational scenarios[6].
Strengths: Comprehensive multi-scale modeling approach, strong integration of experimental and field data. Weaknesses: Complexity of models may lead to longer computation times, potential challenges in real-time applications.
Breakthrough Algorithms for Accurate Predictions
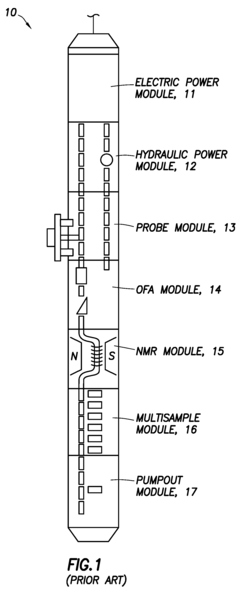
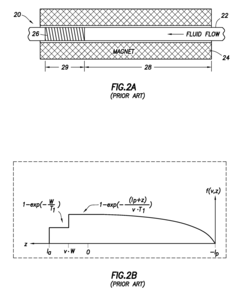
Flow measurement using NMR
PatentActiveUS7459907B2
Innovation
- A nuclear magnetic resonance (NMR) tool and method that apply a radio frequency pulse sequence and magnetic field gradient pulse sequence to measure NMR signals, determining the phase characteristic and velocity distribution of flowing fluids without prior knowledge of T1 distributions, using a combination of NMR sensors and gradient coils to generate pulsed magnetic field gradients.
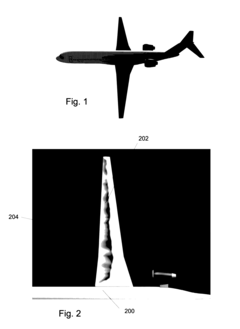
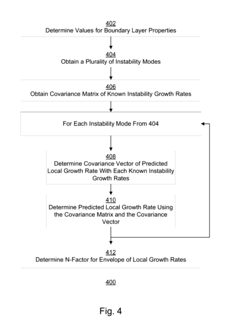
Predicting transition from laminar to turbulent flow over a surface using mode-shape parameters
PatentActiveUS20170045417A1
Innovation
- A method using mode-shape parameters, including boundary-layer properties and instability modes, to predict the transition point by generating a growth-rate model that reduces user interaction and improves simulation efficiency, allowing for accurate prediction of laminar to turbulent flow transitions on computer-generated aircraft surfaces.
Computational Resources and Efficiency
Modeling laminar flow for accurate predictions requires significant computational resources and efficiency considerations. The complexity of fluid dynamics simulations demands powerful hardware and optimized software to achieve reliable results within reasonable timeframes. High-performance computing (HPC) clusters are often employed to handle the intensive calculations involved in laminar flow modeling. These clusters utilize parallel processing techniques to distribute the computational load across multiple nodes, significantly reducing simulation time.
The choice of numerical methods and algorithms plays a crucial role in computational efficiency. Finite element methods (FEM) and finite volume methods (FVM) are commonly used for discretizing the governing equations of laminar flow. Advanced numerical schemes, such as higher-order methods and adaptive mesh refinement techniques, can enhance accuracy while minimizing computational overhead. Implementing these methods effectively requires careful consideration of memory usage and data structures to optimize performance.
Software optimization is another critical aspect of improving computational efficiency in laminar flow modeling. Vectorization and GPU acceleration techniques can dramatically speed up calculations, particularly for large-scale simulations. Specialized libraries and frameworks, such as OpenFOAM and ANSYS Fluent, offer highly optimized solvers tailored for fluid dynamics problems. These tools often incorporate advanced parallelization strategies and efficient algorithms to maximize resource utilization.
Data management and storage considerations are essential when dealing with the vast amounts of information generated during laminar flow simulations. Efficient I/O operations and data compression techniques can significantly reduce storage requirements and improve overall performance. Additionally, implementing checkpointing mechanisms allows for the resumption of simulations in case of system failures, minimizing data loss and computational waste.
As the complexity of laminar flow models increases, so does the need for scalable solutions. Cloud computing platforms offer flexible and scalable resources that can be dynamically allocated based on simulation requirements. This approach allows researchers and engineers to access powerful computational resources on-demand, without the need for significant upfront investments in hardware infrastructure. However, careful consideration must be given to data security and transfer speeds when utilizing cloud-based solutions for sensitive or large-scale simulations.
The choice of numerical methods and algorithms plays a crucial role in computational efficiency. Finite element methods (FEM) and finite volume methods (FVM) are commonly used for discretizing the governing equations of laminar flow. Advanced numerical schemes, such as higher-order methods and adaptive mesh refinement techniques, can enhance accuracy while minimizing computational overhead. Implementing these methods effectively requires careful consideration of memory usage and data structures to optimize performance.
Software optimization is another critical aspect of improving computational efficiency in laminar flow modeling. Vectorization and GPU acceleration techniques can dramatically speed up calculations, particularly for large-scale simulations. Specialized libraries and frameworks, such as OpenFOAM and ANSYS Fluent, offer highly optimized solvers tailored for fluid dynamics problems. These tools often incorporate advanced parallelization strategies and efficient algorithms to maximize resource utilization.
Data management and storage considerations are essential when dealing with the vast amounts of information generated during laminar flow simulations. Efficient I/O operations and data compression techniques can significantly reduce storage requirements and improve overall performance. Additionally, implementing checkpointing mechanisms allows for the resumption of simulations in case of system failures, minimizing data loss and computational waste.
As the complexity of laminar flow models increases, so does the need for scalable solutions. Cloud computing platforms offer flexible and scalable resources that can be dynamically allocated based on simulation requirements. This approach allows researchers and engineers to access powerful computational resources on-demand, without the need for significant upfront investments in hardware infrastructure. However, careful consideration must be given to data security and transfer speeds when utilizing cloud-based solutions for sensitive or large-scale simulations.
Validation Methods for Laminar Flow Models
Validation of laminar flow models is crucial for ensuring accurate predictions in fluid dynamics simulations. The process typically involves comparing model outputs with experimental data or analytical solutions. One common method is the use of benchmark cases, such as flow through a straight pipe or between parallel plates, where analytical solutions are well-established. These cases allow for direct comparison of velocity profiles, pressure drops, and other flow characteristics.
Another validation approach involves the use of particle image velocimetry (PIV) or laser Doppler velocimetry (LDV) to obtain detailed experimental flow field measurements. These techniques provide high-resolution velocity data that can be compared with model predictions at multiple points within the flow domain. This comparison helps identify any discrepancies in the model's ability to capture local flow features accurately.
Grid convergence studies are essential for validating the numerical aspects of laminar flow models. By systematically refining the computational mesh and comparing results, researchers can assess the model's sensitivity to spatial discretization and ensure that the solution is independent of grid resolution. This process helps establish the minimum grid requirements for accurate predictions.
Sensitivity analyses are also valuable for model validation. By varying input parameters such as fluid properties, boundary conditions, or geometric features, researchers can evaluate the model's robustness and identify potential sources of error. This approach helps quantify the uncertainty associated with model predictions and provides insights into the model's limitations.
For more complex geometries or flow conditions, researchers often employ advanced visualization techniques to compare experimental and simulated flow patterns. These may include dye injection experiments or computational flow visualization methods, allowing for qualitative assessment of the model's ability to capture flow structures and patterns accurately.
Statistical methods play a crucial role in quantifying the agreement between model predictions and experimental data. Techniques such as root mean square error (RMSE) analysis, correlation coefficients, and goodness-of-fit tests provide objective measures of model performance. These metrics help researchers assess the overall accuracy of the laminar flow model and identify areas for improvement.
Validation efforts should also consider the model's ability to predict derived quantities, such as heat transfer coefficients or drag forces, which are often of practical interest in engineering applications. Comparing these derived quantities with experimental measurements or correlations from literature provides additional confidence in the model's predictive capabilities.
Another validation approach involves the use of particle image velocimetry (PIV) or laser Doppler velocimetry (LDV) to obtain detailed experimental flow field measurements. These techniques provide high-resolution velocity data that can be compared with model predictions at multiple points within the flow domain. This comparison helps identify any discrepancies in the model's ability to capture local flow features accurately.
Grid convergence studies are essential for validating the numerical aspects of laminar flow models. By systematically refining the computational mesh and comparing results, researchers can assess the model's sensitivity to spatial discretization and ensure that the solution is independent of grid resolution. This process helps establish the minimum grid requirements for accurate predictions.
Sensitivity analyses are also valuable for model validation. By varying input parameters such as fluid properties, boundary conditions, or geometric features, researchers can evaluate the model's robustness and identify potential sources of error. This approach helps quantify the uncertainty associated with model predictions and provides insights into the model's limitations.
For more complex geometries or flow conditions, researchers often employ advanced visualization techniques to compare experimental and simulated flow patterns. These may include dye injection experiments or computational flow visualization methods, allowing for qualitative assessment of the model's ability to capture flow structures and patterns accurately.
Statistical methods play a crucial role in quantifying the agreement between model predictions and experimental data. Techniques such as root mean square error (RMSE) analysis, correlation coefficients, and goodness-of-fit tests provide objective measures of model performance. These metrics help researchers assess the overall accuracy of the laminar flow model and identify areas for improvement.
Validation efforts should also consider the model's ability to predict derived quantities, such as heat transfer coefficients or drag forces, which are often of practical interest in engineering applications. Comparing these derived quantities with experimental measurements or correlations from literature provides additional confidence in the model's predictive capabilities.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!