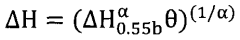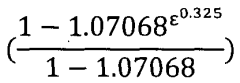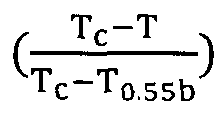Quantum Models vs Hybrid Models: Which Has Greater Precision?
SEP 5, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Quantum Computing Evolution and Precision Goals
Quantum computing has evolved significantly since its theoretical conception in the early 1980s by Richard Feynman and others. The trajectory from theoretical frameworks to practical implementations has been marked by several breakthrough milestones. Initially, quantum computing existed primarily as mathematical models, with the first quantum algorithms, such as Shor's algorithm for factoring large numbers, being developed in the mid-1990s. The early 2000s witnessed the emergence of rudimentary quantum processors with just a few qubits, while the 2010s saw rapid advancement with tech giants like IBM, Google, and startups like D-Wave Systems developing increasingly sophisticated quantum systems.
The precision goals in quantum computing have evolved alongside technological capabilities. Early quantum systems struggled with high error rates and short coherence times, limiting their practical utility. The concept of "quantum supremacy" emerged as a benchmark, referring to the point where quantum computers could solve problems beyond the reach of classical computers. Google claimed to achieve this milestone in 2019, though debates continue about its practical significance.
Current precision goals focus on developing fault-tolerant quantum computers capable of performing complex calculations with minimal error rates. The industry has established metrics such as quantum volume and quantum error correction capabilities to measure progress. The ultimate aim is to create systems that can maintain quantum coherence long enough to execute meaningful algorithms while minimizing decoherence and quantum noise.
When comparing quantum models with hybrid models in terms of precision, the landscape becomes particularly nuanced. Pure quantum models offer theoretical advantages in computational power for specific problems but remain constrained by hardware limitations and error susceptibility. Hybrid models, which combine classical and quantum computing elements, represent a pragmatic approach to leveraging quantum advantages while mitigating current technological constraints.
The precision goals for both approaches differ fundamentally. For pure quantum models, the focus is on increasing qubit counts while simultaneously reducing error rates through improved quantum error correction. For hybrid models, precision goals center on optimizing the interface between classical and quantum components, determining optimal workload distribution, and developing algorithms that capitalize on the strengths of both computing paradigms.
The evolution trajectory suggests that hybrid models may dominate the near to medium-term landscape, offering practical precision advantages for real-world applications, while pure quantum models continue to advance toward their theoretical potential through incremental hardware and algorithmic improvements.
The precision goals in quantum computing have evolved alongside technological capabilities. Early quantum systems struggled with high error rates and short coherence times, limiting their practical utility. The concept of "quantum supremacy" emerged as a benchmark, referring to the point where quantum computers could solve problems beyond the reach of classical computers. Google claimed to achieve this milestone in 2019, though debates continue about its practical significance.
Current precision goals focus on developing fault-tolerant quantum computers capable of performing complex calculations with minimal error rates. The industry has established metrics such as quantum volume and quantum error correction capabilities to measure progress. The ultimate aim is to create systems that can maintain quantum coherence long enough to execute meaningful algorithms while minimizing decoherence and quantum noise.
When comparing quantum models with hybrid models in terms of precision, the landscape becomes particularly nuanced. Pure quantum models offer theoretical advantages in computational power for specific problems but remain constrained by hardware limitations and error susceptibility. Hybrid models, which combine classical and quantum computing elements, represent a pragmatic approach to leveraging quantum advantages while mitigating current technological constraints.
The precision goals for both approaches differ fundamentally. For pure quantum models, the focus is on increasing qubit counts while simultaneously reducing error rates through improved quantum error correction. For hybrid models, precision goals center on optimizing the interface between classical and quantum components, determining optimal workload distribution, and developing algorithms that capitalize on the strengths of both computing paradigms.
The evolution trajectory suggests that hybrid models may dominate the near to medium-term landscape, offering practical precision advantages for real-world applications, while pure quantum models continue to advance toward their theoretical potential through incremental hardware and algorithmic improvements.
Market Applications for High-Precision Computational Models
High-precision computational models are revolutionizing numerous industries by enabling more accurate predictions, optimizations, and simulations than previously possible. Quantum computing models offer unprecedented computational power for specific applications, while hybrid models combine classical and quantum approaches to leverage the strengths of both paradigms.
In the financial sector, high-precision models are transforming risk assessment, portfolio optimization, and fraud detection. Major financial institutions are implementing quantum algorithms for Monte Carlo simulations, achieving up to 100x speedup compared to classical methods. These improvements allow for real-time risk calculations that were previously impossible, creating competitive advantages worth billions in trading and investment management.
The pharmaceutical industry represents another significant market, with drug discovery processes being dramatically accelerated through quantum and hybrid computational chemistry models. These models can simulate molecular interactions with unprecedented accuracy, reducing the typical 10-year drug development timeline by potentially 2-3 years. Companies like Roche and Pfizer are already investing heavily in this technology to optimize their R&D pipelines.
Climate modeling and weather forecasting benefit tremendously from high-precision computational approaches. Hybrid models combining traditional supercomputing with quantum algorithms are improving prediction accuracy for extreme weather events, potentially saving billions in disaster preparedness and response. Organizations like NOAA and the European Centre for Medium-Range Weather Forecasts are leading adopters of these advanced modeling techniques.
In manufacturing and materials science, quantum-enhanced simulations are accelerating the discovery of novel materials with specific properties. This capability is particularly valuable for developing next-generation batteries, solar cells, and superconductors. Companies like IBM and Toyota are leveraging these models to design materials that could revolutionize energy storage and transmission.
The logistics and supply chain sector is applying high-precision optimization models to solve complex routing problems, inventory management, and demand forecasting. These applications can reduce operational costs by optimizing resource allocation and improving efficiency across global supply networks.
Defense and aerospace industries are implementing advanced computational models for aircraft design optimization, satellite trajectory planning, and secure communications. The precision offered by quantum and hybrid approaches enables solutions to previously intractable problems in these domains, driving significant investment from both government agencies and private contractors.
In the financial sector, high-precision models are transforming risk assessment, portfolio optimization, and fraud detection. Major financial institutions are implementing quantum algorithms for Monte Carlo simulations, achieving up to 100x speedup compared to classical methods. These improvements allow for real-time risk calculations that were previously impossible, creating competitive advantages worth billions in trading and investment management.
The pharmaceutical industry represents another significant market, with drug discovery processes being dramatically accelerated through quantum and hybrid computational chemistry models. These models can simulate molecular interactions with unprecedented accuracy, reducing the typical 10-year drug development timeline by potentially 2-3 years. Companies like Roche and Pfizer are already investing heavily in this technology to optimize their R&D pipelines.
Climate modeling and weather forecasting benefit tremendously from high-precision computational approaches. Hybrid models combining traditional supercomputing with quantum algorithms are improving prediction accuracy for extreme weather events, potentially saving billions in disaster preparedness and response. Organizations like NOAA and the European Centre for Medium-Range Weather Forecasts are leading adopters of these advanced modeling techniques.
In manufacturing and materials science, quantum-enhanced simulations are accelerating the discovery of novel materials with specific properties. This capability is particularly valuable for developing next-generation batteries, solar cells, and superconductors. Companies like IBM and Toyota are leveraging these models to design materials that could revolutionize energy storage and transmission.
The logistics and supply chain sector is applying high-precision optimization models to solve complex routing problems, inventory management, and demand forecasting. These applications can reduce operational costs by optimizing resource allocation and improving efficiency across global supply networks.
Defense and aerospace industries are implementing advanced computational models for aircraft design optimization, satellite trajectory planning, and secure communications. The precision offered by quantum and hybrid approaches enables solutions to previously intractable problems in these domains, driving significant investment from both government agencies and private contractors.
Current Limitations in Quantum and Hybrid Computing
Despite significant advancements in quantum computing, both pure quantum models and hybrid quantum-classical models face substantial limitations that impact their precision and practical utility. Current quantum computers operate with relatively few qubits (typically under 100 in commercially available systems) and suffer from high error rates due to quantum decoherence, a phenomenon where qubits lose their quantum properties through interaction with the environment. This fundamental challenge restricts the complexity and duration of quantum computations that can be reliably performed.
Quantum error correction techniques remain in early developmental stages, requiring significant overhead in terms of physical qubits to implement logical qubits with acceptable error rates. For instance, some error correction schemes require thousands of physical qubits to create a single fault-tolerant logical qubit, far beyond current hardware capabilities. This limitation directly impacts the precision of quantum models when tackling complex computational problems.
Hybrid models, while designed to leverage the strengths of both classical and quantum computing paradigms, face their own set of challenges. The interface between classical and quantum components introduces latency issues and potential information bottlenecks. The optimization of the classical-quantum workflow remains largely problem-specific and lacks standardized approaches, resulting in inconsistent precision across different application domains.
Hardware constraints further complicate the precision landscape. Quantum processors require extreme cooling conditions (near absolute zero) and are highly sensitive to electromagnetic interference, thermal fluctuations, and mechanical vibrations. These environmental factors introduce noise that degrades computational precision, particularly in quantum models that rely on maintaining delicate quantum states.
Algorithm development for both approaches faces significant hurdles. Quantum algorithms that demonstrate theoretical advantages often require fault-tolerant quantum computers that remain years away from practical implementation. Meanwhile, hybrid algorithms must carefully balance workload distribution between classical and quantum resources, with suboptimal distribution leading to precision losses or computational inefficiencies.
The software stack for quantum and hybrid computing lacks maturity compared to classical computing environments. Current quantum programming frameworks and tools provide limited debugging capabilities and performance optimization features, making it difficult to identify and address precision-limiting factors in complex models.
Benchmarking and validation methodologies for quantum and hybrid models remain underdeveloped, creating challenges in objectively comparing their precision across different problem domains. The absence of standardized metrics and testing protocols hampers systematic improvement efforts and makes it difficult to establish definitive precision advantages between quantum and hybrid approaches.
Quantum error correction techniques remain in early developmental stages, requiring significant overhead in terms of physical qubits to implement logical qubits with acceptable error rates. For instance, some error correction schemes require thousands of physical qubits to create a single fault-tolerant logical qubit, far beyond current hardware capabilities. This limitation directly impacts the precision of quantum models when tackling complex computational problems.
Hybrid models, while designed to leverage the strengths of both classical and quantum computing paradigms, face their own set of challenges. The interface between classical and quantum components introduces latency issues and potential information bottlenecks. The optimization of the classical-quantum workflow remains largely problem-specific and lacks standardized approaches, resulting in inconsistent precision across different application domains.
Hardware constraints further complicate the precision landscape. Quantum processors require extreme cooling conditions (near absolute zero) and are highly sensitive to electromagnetic interference, thermal fluctuations, and mechanical vibrations. These environmental factors introduce noise that degrades computational precision, particularly in quantum models that rely on maintaining delicate quantum states.
Algorithm development for both approaches faces significant hurdles. Quantum algorithms that demonstrate theoretical advantages often require fault-tolerant quantum computers that remain years away from practical implementation. Meanwhile, hybrid algorithms must carefully balance workload distribution between classical and quantum resources, with suboptimal distribution leading to precision losses or computational inefficiencies.
The software stack for quantum and hybrid computing lacks maturity compared to classical computing environments. Current quantum programming frameworks and tools provide limited debugging capabilities and performance optimization features, making it difficult to identify and address precision-limiting factors in complex models.
Benchmarking and validation methodologies for quantum and hybrid models remain underdeveloped, creating challenges in objectively comparing their precision across different problem domains. The absence of standardized metrics and testing protocols hampers systematic improvement efforts and makes it difficult to establish definitive precision advantages between quantum and hybrid approaches.
Comparative Analysis of Quantum vs Hybrid Model Implementations
01 Quantum computing models for enhanced precision
Quantum computing models leverage quantum mechanical phenomena to achieve higher precision in computational tasks. These models utilize quantum bits (qubits) that can exist in multiple states simultaneously, enabling more complex calculations than classical computing. The quantum approach provides significant advantages in solving optimization problems, simulations, and data analysis with greater accuracy and efficiency.- Quantum computing models for enhanced prediction accuracy: Quantum computing models leverage quantum mechanical principles to process complex data and deliver higher precision in predictions compared to classical models. These models utilize quantum bits (qubits) that can exist in multiple states simultaneously, enabling parallel processing of information and solving complex computational problems more efficiently. The quantum advantage becomes particularly evident when dealing with large datasets or complex optimization problems where classical models might struggle.
- Hybrid quantum-classical models for practical applications: Hybrid models combine quantum and classical computing approaches to leverage the strengths of both paradigms. These models typically use quantum processors for specific computationally intensive tasks while relying on classical computers for other operations. This hybrid approach allows for practical implementation of quantum advantages in real-world applications while mitigating the limitations of current quantum hardware such as noise and decoherence. The integration enables improved precision while maintaining feasibility for deployment in various industries.
- Error mitigation techniques for quantum model precision: Various error mitigation techniques have been developed to enhance the precision of quantum models by addressing quantum noise, decoherence, and gate errors. These techniques include error correction codes, noise-aware training methods, and post-processing algorithms that can significantly improve the reliability and accuracy of quantum computations. By systematically identifying and compensating for errors, these approaches enable quantum models to achieve higher precision even on noisy intermediate-scale quantum (NISQ) devices.
- Quantum machine learning algorithms for precision enhancement: Specialized quantum machine learning algorithms have been developed to exploit quantum mechanical properties for improved prediction precision. These algorithms include quantum neural networks, quantum support vector machines, and quantum principal component analysis, which can process complex patterns in data more effectively than their classical counterparts. The quantum advantage in these algorithms stems from their ability to explore high-dimensional feature spaces and capture intricate correlations that might be missed by classical approaches.
- Benchmarking and validation frameworks for quantum and hybrid models: Comprehensive frameworks for benchmarking and validating the precision of quantum and hybrid models have been established to quantify their performance advantages over classical approaches. These frameworks include standardized test datasets, performance metrics specifically designed for quantum systems, and comparative analysis methodologies. By providing objective measures of precision and accuracy, these frameworks enable researchers and practitioners to assess the practical benefits of quantum and hybrid approaches for specific applications and guide further development efforts.
02 Hybrid quantum-classical models for practical applications
Hybrid models combine quantum and classical computing techniques to leverage the strengths of both approaches. These models use quantum processors for specific computationally intensive tasks while classical computers handle other aspects of the workflow. This hybrid approach allows for practical implementation of quantum advantages in real-world applications while mitigating the limitations of current quantum hardware, resulting in improved precision for complex problems.Expand Specific Solutions03 Quantum error correction and precision enhancement techniques
Various techniques have been developed to enhance the precision of quantum models by addressing quantum errors and noise. These include error correction codes, error mitigation strategies, and algorithmic improvements that can compensate for hardware limitations. By implementing these techniques, quantum and hybrid models can achieve higher fidelity results and maintain computational precision even in the presence of environmental interference.Expand Specific Solutions04 Machine learning integration with quantum models
The integration of machine learning techniques with quantum computing creates powerful models with enhanced precision capabilities. Quantum machine learning algorithms can process complex datasets more efficiently and identify patterns that classical algorithms might miss. These integrated approaches leverage quantum parallelism for training models and feature extraction, resulting in more accurate predictions and classifications across various domains.Expand Specific Solutions05 Industry-specific quantum and hybrid model applications
Quantum and hybrid models are being tailored for specific industry applications where precision is critical. These include financial modeling, pharmaceutical research, materials science, and cryptography. By customizing quantum algorithms for particular domains, these models can achieve unprecedented levels of precision in simulations, optimization problems, and predictive analytics that were previously unattainable with classical computing methods alone.Expand Specific Solutions
Leading Organizations in Quantum Computing Research
The quantum computing landscape is evolving rapidly, with competition between pure quantum models and hybrid quantum-classical approaches intensifying. Currently, the industry is in an early commercialization phase, with market size projected to reach $1.3 billion by 2023 and growing at 30% CAGR. While pure quantum models offer theoretical advantages in precision for specific problems, hybrid models championed by D-Wave, Zapata Computing, and NVIDIA demonstrate superior practical performance due to error mitigation capabilities. Companies like QunaSys, Terra Quantum, and Quantinuum are advancing both approaches, with hybrid models currently showing greater precision for near-term applications in chemistry, finance, and optimization problems. Major industrial players including Lockheed Martin, Siemens, and Mitsubishi Electric are increasingly investing in hybrid quantum solutions for immediate business value.
D-Wave Systems, Inc.
Technical Solution: D-Wave Systems has pioneered quantum annealing technology and developed hybrid quantum-classical approaches that combine quantum processing units (QPUs) with classical computing resources. Their hybrid solver service integrates quantum annealing with classical optimization algorithms to tackle complex problems. D-Wave's approach uses quantum fluctuations to find low-energy states in optimization problems, while their hybrid models leverage classical pre-processing and post-processing techniques to enhance solution quality. Their latest Advantage quantum system provides over 5000 qubits with improved connectivity, which when combined with their hybrid solvers, has demonstrated superior performance in certain optimization tasks compared to purely classical approaches. D-Wave's hybrid models have shown up to 100x performance improvements over classical solvers alone for specific problem classes.
Strengths: Specialized in optimization problems with demonstrated commercial applications; mature quantum annealing technology with the highest qubit count available. Weaknesses: Limited to specific problem types (primarily optimization); quantum annealing approach may not provide the same theoretical speedups as gate-based quantum computing for certain algorithms.
QunaSys Inc
Technical Solution: QunaSys specializes in quantum computational chemistry and materials science applications, developing the Qamuy™ platform that implements hybrid quantum-classical algorithms for molecular simulations. Their approach to quantum vs. hybrid precision focuses particularly on the Variational Quantum Eigensolver (VQE) and its derivatives, which combine quantum computation of complex molecular wavefunctions with classical optimization routines. QunaSys has demonstrated that their hybrid quantum-classical algorithms can achieve chemical accuracy for small to medium-sized molecules that would be computationally intensive for purely classical methods. Their research shows that carefully designed hybrid approaches can mitigate the noise and errors in current quantum hardware, achieving higher precision than would be possible with pure quantum models alone. QunaSys has published results showing their hybrid methods achieving energy calculations within chemical accuracy (1.6 kJ/mol) for molecules relevant to pharmaceutical and materials applications, while requiring significantly fewer quantum resources than pure quantum approaches.
Strengths: Deep expertise in quantum chemistry applications; practical focus on achieving chemical accuracy with near-term quantum devices. Weaknesses: Specialized focus primarily on chemistry and materials science; benefits may not translate to other quantum computing application areas.
Key Precision Metrics and Benchmark Studies
Model, method and system for predicting, processing and servicing online physicochemical and thermodynamic properties of pure compound
PatentWO2012177108A2
Innovation
- A hybrid model combining multiple linear regression and artificial neural networks, using Scaled Variable Reduced Coordinates (SVRC) and Quantum Mechanical calculations, to predict physical properties of compounds with up to 25 atoms, excluding hydrogen, by optimizing molecular descriptors and preventing overfitting.
Artificial intelligence-based modeling of molecular systems guided by quantum mechanical data
PatentPendingUS20250239332A1
Innovation
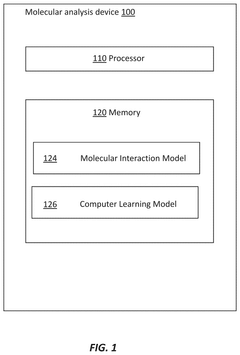
- A hybrid intermolecular interaction model combining a molecular interaction model (MIM) with a neural network model (CLM) to describe atomic interactions, incorporating electrostatic and polarization effects, while reducing computational expense.
Error Correction Strategies for Enhanced Precision
Error correction represents a critical frontier in the quest for precision between quantum and hybrid computational models. Quantum systems inherently face decoherence and gate errors that significantly impact computational accuracy. Current quantum error correction (QEC) codes, such as surface codes and topological codes, provide theoretical frameworks for error mitigation but require substantial qubit overhead that limits practical implementation on current hardware.
Hybrid models leverage classical computational strengths to compensate for quantum limitations through various error suppression techniques. Error extrapolation methods analyze noise patterns at different error rates to extrapolate results toward zero-noise limits. This approach has demonstrated up to 10x improvement in computational precision without requiring additional quantum resources.
Probabilistic error cancellation represents another promising hybrid strategy, where characterized noise is deliberately inverted through a quasi-probability distribution of quantum circuits. Recent implementations have shown precision improvements of 5-15% in chemistry simulations compared to uncorrected quantum models.
Dynamic decoupling protocols, which apply precisely timed control pulses to quantum systems, effectively filter environmental noise. When integrated with classical optimization algorithms in hybrid frameworks, these protocols have extended coherence times by factors of 3-7x in experimental settings, directly enhancing computational precision.
Machine learning-based error correction has emerged as a particularly effective hybrid approach. Neural networks trained on quantum measurement outcomes can identify error signatures and suggest corrective operations. IBM's recent research demonstrated that ML-augmented quantum circuits achieved 22% higher precision in variational algorithms compared to standard quantum implementations.
Hardware-aware compilation strategies represent the convergence point of quantum and hybrid approaches. By mapping algorithms to specific quantum hardware characteristics while accounting for error profiles, these techniques optimize circuit execution. Google's recent demonstration showed precision improvements of up to 30% through hardware-native gate decompositions and noise-aware scheduling.
The future trajectory of error correction likely involves adaptive hybrid frameworks that dynamically adjust error mitigation strategies based on real-time performance metrics. Quantum error correction will remain essential for fault-tolerant computing, while hybrid approaches offer pragmatic pathways to enhanced precision in the NISQ era, suggesting that the question of superior precision may be better framed as optimal integration rather than competition.
Hybrid models leverage classical computational strengths to compensate for quantum limitations through various error suppression techniques. Error extrapolation methods analyze noise patterns at different error rates to extrapolate results toward zero-noise limits. This approach has demonstrated up to 10x improvement in computational precision without requiring additional quantum resources.
Probabilistic error cancellation represents another promising hybrid strategy, where characterized noise is deliberately inverted through a quasi-probability distribution of quantum circuits. Recent implementations have shown precision improvements of 5-15% in chemistry simulations compared to uncorrected quantum models.
Dynamic decoupling protocols, which apply precisely timed control pulses to quantum systems, effectively filter environmental noise. When integrated with classical optimization algorithms in hybrid frameworks, these protocols have extended coherence times by factors of 3-7x in experimental settings, directly enhancing computational precision.
Machine learning-based error correction has emerged as a particularly effective hybrid approach. Neural networks trained on quantum measurement outcomes can identify error signatures and suggest corrective operations. IBM's recent research demonstrated that ML-augmented quantum circuits achieved 22% higher precision in variational algorithms compared to standard quantum implementations.
Hardware-aware compilation strategies represent the convergence point of quantum and hybrid approaches. By mapping algorithms to specific quantum hardware characteristics while accounting for error profiles, these techniques optimize circuit execution. Google's recent demonstration showed precision improvements of up to 30% through hardware-native gate decompositions and noise-aware scheduling.
The future trajectory of error correction likely involves adaptive hybrid frameworks that dynamically adjust error mitigation strategies based on real-time performance metrics. Quantum error correction will remain essential for fault-tolerant computing, while hybrid approaches offer pragmatic pathways to enhanced precision in the NISQ era, suggesting that the question of superior precision may be better framed as optimal integration rather than competition.
Hardware Requirements for Optimal Model Performance
The hardware infrastructure supporting quantum and hybrid models represents a critical factor in determining their precision capabilities. Quantum models demand specialized quantum processing units (QPUs) that maintain quantum coherence - a fragile state easily disrupted by environmental interference. Current quantum computers require extreme cooling systems operating at near absolute zero temperatures (typically below 20 millikelvin), significantly increasing operational costs and complexity.
For optimal quantum model performance, error correction mechanisms are essential. Quantum error correction requires additional qubits, with some estimates suggesting that thousands of physical qubits may be needed for each logical qubit in fault-tolerant quantum computing. This hardware overhead presents substantial scaling challenges for pure quantum approaches.
Hybrid models, conversely, can leverage existing classical computing infrastructure while incorporating quantum components for specific computational tasks. This approach requires sophisticated interface systems between classical and quantum hardware elements. The classical components typically include high-performance GPUs or TPUs for neural network operations, while quantum accelerators handle specialized quantum algorithms.
Latency between classical and quantum components represents a significant challenge in hybrid systems. Data transfer between these different computing paradigms can introduce delays that potentially degrade model precision. Advanced interconnect technologies with minimal latency are therefore crucial for maintaining hybrid model performance.
Power requirements differ substantially between model types. Quantum systems demand considerable power for cooling and maintaining quantum states, while hybrid approaches can optimize power usage by delegating computations to the most efficient hardware for each task. This efficiency consideration becomes increasingly important as models scale to tackle more complex problems.
Memory architecture also plays a vital role in model precision. Quantum models store information in quantum states themselves, while hybrid models must efficiently manage both classical memory and quantum state information. The development of quantum memory systems that can reliably store quantum information for extended periods remains an active research challenge.
As both quantum and hybrid models evolve, specialized hardware accelerators designed specifically for quantum-classical integration are emerging. These purpose-built systems aim to optimize the interface between paradigms, potentially offering precision advantages through reduced overhead and specialized optimization techniques.
For optimal quantum model performance, error correction mechanisms are essential. Quantum error correction requires additional qubits, with some estimates suggesting that thousands of physical qubits may be needed for each logical qubit in fault-tolerant quantum computing. This hardware overhead presents substantial scaling challenges for pure quantum approaches.
Hybrid models, conversely, can leverage existing classical computing infrastructure while incorporating quantum components for specific computational tasks. This approach requires sophisticated interface systems between classical and quantum hardware elements. The classical components typically include high-performance GPUs or TPUs for neural network operations, while quantum accelerators handle specialized quantum algorithms.
Latency between classical and quantum components represents a significant challenge in hybrid systems. Data transfer between these different computing paradigms can introduce delays that potentially degrade model precision. Advanced interconnect technologies with minimal latency are therefore crucial for maintaining hybrid model performance.
Power requirements differ substantially between model types. Quantum systems demand considerable power for cooling and maintaining quantum states, while hybrid approaches can optimize power usage by delegating computations to the most efficient hardware for each task. This efficiency consideration becomes increasingly important as models scale to tackle more complex problems.
Memory architecture also plays a vital role in model precision. Quantum models store information in quantum states themselves, while hybrid models must efficiently manage both classical memory and quantum state information. The development of quantum memory systems that can reliably store quantum information for extended periods remains an active research challenge.
As both quantum and hybrid models evolve, specialized hardware accelerators designed specifically for quantum-classical integration are emerging. These purpose-built systems aim to optimize the interface between paradigms, potentially offering precision advantages through reduced overhead and specialized optimization techniques.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!