Compare Kalman Filter Vs Hidden Markov Models For Prediction
SEP 12, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter and HMM Background and Objectives
Kalman Filter and Hidden Markov Models (HMMs) represent two foundational mathematical frameworks in the field of state estimation and prediction, each with distinct historical development paths and theoretical underpinnings. The Kalman Filter, introduced by Rudolf E. Kalman in 1960, emerged from control theory and aerospace applications, initially developed to solve spacecraft navigation problems during the Apollo missions. This recursive algorithm has since evolved through variants like Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF) to address nonlinear systems.
Meanwhile, Hidden Markov Models originated from statistical modeling in the late 1960s, with significant contributions from Leonard E. Baum and Lloyd Welch. HMMs gained prominence in the 1980s through speech recognition applications before expanding to various pattern recognition domains. Both technologies have experienced parallel evolution, with computational advances enabling their widespread implementation across diverse fields.
The current technological landscape shows increasing convergence between these methodologies, particularly in hybrid approaches that leverage the complementary strengths of each framework. Recent research focuses on addressing the fundamental limitations of both techniques: Kalman Filters' challenges with non-Gaussian noise and highly nonlinear systems, and HMMs' difficulties with continuous state spaces and temporal dependencies beyond first-order Markov assumptions.
Our technical objective in this research is to conduct a comprehensive comparative analysis of Kalman Filters and Hidden Markov Models for prediction tasks across various domains. We aim to establish clear guidelines for selecting the appropriate framework based on specific application requirements, data characteristics, and computational constraints. This includes quantifying performance differences in terms of prediction accuracy, computational efficiency, and robustness under varying conditions.
Additionally, we seek to identify potential synergies between these approaches, exploring hybrid models that combine the continuous state estimation capabilities of Kalman Filters with the discrete state transition modeling of HMMs. The ultimate goal is to develop a unified framework that can adaptively select or blend these techniques based on the specific prediction context, potentially overcoming the individual limitations of each approach.
This research will contribute to advancing predictive analytics by providing practitioners with clearer decision criteria for algorithm selection and highlighting promising directions for algorithmic innovation that bridges these two established methodologies. The findings will particularly benefit emerging applications in autonomous systems, financial forecasting, and biomedical signal processing where prediction accuracy under uncertainty is critical.
Meanwhile, Hidden Markov Models originated from statistical modeling in the late 1960s, with significant contributions from Leonard E. Baum and Lloyd Welch. HMMs gained prominence in the 1980s through speech recognition applications before expanding to various pattern recognition domains. Both technologies have experienced parallel evolution, with computational advances enabling their widespread implementation across diverse fields.
The current technological landscape shows increasing convergence between these methodologies, particularly in hybrid approaches that leverage the complementary strengths of each framework. Recent research focuses on addressing the fundamental limitations of both techniques: Kalman Filters' challenges with non-Gaussian noise and highly nonlinear systems, and HMMs' difficulties with continuous state spaces and temporal dependencies beyond first-order Markov assumptions.
Our technical objective in this research is to conduct a comprehensive comparative analysis of Kalman Filters and Hidden Markov Models for prediction tasks across various domains. We aim to establish clear guidelines for selecting the appropriate framework based on specific application requirements, data characteristics, and computational constraints. This includes quantifying performance differences in terms of prediction accuracy, computational efficiency, and robustness under varying conditions.
Additionally, we seek to identify potential synergies between these approaches, exploring hybrid models that combine the continuous state estimation capabilities of Kalman Filters with the discrete state transition modeling of HMMs. The ultimate goal is to develop a unified framework that can adaptively select or blend these techniques based on the specific prediction context, potentially overcoming the individual limitations of each approach.
This research will contribute to advancing predictive analytics by providing practitioners with clearer decision criteria for algorithm selection and highlighting promising directions for algorithmic innovation that bridges these two established methodologies. The findings will particularly benefit emerging applications in autonomous systems, financial forecasting, and biomedical signal processing where prediction accuracy under uncertainty is critical.
Market Applications and Demand Analysis
The market for predictive analytics technologies has experienced substantial growth over the past decade, with Kalman Filters and Hidden Markov Models (HMMs) emerging as critical components in various industry applications. The global predictive analytics market reached approximately $10.5 billion in 2021 and is projected to grow at a CAGR of 21.5% through 2028, driven by increasing demand for advanced forecasting capabilities across multiple sectors.
In the autonomous vehicle industry, Kalman Filters have established dominance due to their superior performance in real-time tracking and prediction of moving objects. Major automotive manufacturers and technology companies have integrated Kalman Filter algorithms into their sensor fusion systems, creating a market segment valued at over $2.3 billion in 2022. The demand for these systems is expected to triple by 2027 as autonomous vehicle adoption accelerates.
Financial services represent another significant market for both technologies, with HMMs finding particular application in market trend prediction and risk assessment. Investment banks and hedge funds increasingly rely on HMMs for pattern recognition in financial time series data, contributing to a specialized analytics market worth approximately $1.8 billion annually. The ability of HMMs to identify hidden states in seemingly random financial data provides competitive advantages in algorithmic trading platforms.
Healthcare applications demonstrate a growing demand for both technologies, with Kalman Filters predominantly used in medical device tracking and patient monitoring systems. The healthcare predictive analytics market utilizing these technologies reached $1.2 billion in 2022, with hospitals and medical device manufacturers seeking more accurate real-time monitoring solutions. Meanwhile, HMMs have gained traction in disease progression modeling and genomic sequence analysis.
Industrial IoT applications represent the fastest-growing market segment for these technologies, with a projected CAGR of 24.7% through 2027. Manufacturing companies are implementing Kalman Filters for equipment performance prediction and maintenance scheduling, while HMMs are increasingly deployed for complex process monitoring and quality control systems where state transitions must be inferred from limited observable data.
Regional analysis indicates North America currently leads market adoption of both technologies, accounting for approximately 42% of global implementation. However, Asia-Pacific markets are demonstrating the highest growth rates, particularly in manufacturing and automotive applications, with China, Japan, and South Korea making significant investments in research and implementation of advanced predictive algorithms.
In the autonomous vehicle industry, Kalman Filters have established dominance due to their superior performance in real-time tracking and prediction of moving objects. Major automotive manufacturers and technology companies have integrated Kalman Filter algorithms into their sensor fusion systems, creating a market segment valued at over $2.3 billion in 2022. The demand for these systems is expected to triple by 2027 as autonomous vehicle adoption accelerates.
Financial services represent another significant market for both technologies, with HMMs finding particular application in market trend prediction and risk assessment. Investment banks and hedge funds increasingly rely on HMMs for pattern recognition in financial time series data, contributing to a specialized analytics market worth approximately $1.8 billion annually. The ability of HMMs to identify hidden states in seemingly random financial data provides competitive advantages in algorithmic trading platforms.
Healthcare applications demonstrate a growing demand for both technologies, with Kalman Filters predominantly used in medical device tracking and patient monitoring systems. The healthcare predictive analytics market utilizing these technologies reached $1.2 billion in 2022, with hospitals and medical device manufacturers seeking more accurate real-time monitoring solutions. Meanwhile, HMMs have gained traction in disease progression modeling and genomic sequence analysis.
Industrial IoT applications represent the fastest-growing market segment for these technologies, with a projected CAGR of 24.7% through 2027. Manufacturing companies are implementing Kalman Filters for equipment performance prediction and maintenance scheduling, while HMMs are increasingly deployed for complex process monitoring and quality control systems where state transitions must be inferred from limited observable data.
Regional analysis indicates North America currently leads market adoption of both technologies, accounting for approximately 42% of global implementation. However, Asia-Pacific markets are demonstrating the highest growth rates, particularly in manufacturing and automotive applications, with China, Japan, and South Korea making significant investments in research and implementation of advanced predictive algorithms.
Current State and Technical Challenges
Kalman Filters and Hidden Markov Models (HMMs) represent two fundamental approaches to prediction in dynamic systems, each with distinct strengths and limitations in contemporary applications. Currently, Kalman Filters enjoy widespread implementation in aerospace, robotics, and autonomous vehicle navigation due to their computational efficiency and proven reliability in linear systems with Gaussian noise. The Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF) variants have expanded applicability to nonlinear systems, though with increased computational demands.
HMMs, conversely, have established dominance in speech recognition, natural language processing, and biological sequence analysis where discrete state transitions are prevalent. Recent advancements in variational inference methods have enhanced HMM training efficiency, while parallel computing architectures have mitigated some computational constraints.
A significant technical challenge for Kalman Filters remains their fundamental assumption of Gaussian noise distributions, which proves problematic in environments with multi-modal or heavy-tailed noise characteristics. Additionally, the linearization approximations in EKF can introduce substantial errors in highly nonlinear systems, potentially leading to filter divergence and prediction failures.
For HMMs, scalability presents a persistent challenge as state space dimensionality increases, with computational complexity growing exponentially. This "curse of dimensionality" limits practical application in high-dimensional systems without significant model simplification. Furthermore, HMMs struggle with long-range dependencies due to their Markov property assumption, which can be restrictive for complex sequential data.
Geographically, North American research institutions and technology companies lead in Kalman Filter innovations for autonomous systems, while European academic centers have contributed substantial theoretical advancements in HMM applications for natural language processing. Asian research groups, particularly in Japan and China, have made notable progress in hybrid approaches combining elements of both methodologies.
Recent research has focused on particle filters as an alternative that addresses limitations of both approaches, offering more flexible noise distribution handling than Kalman Filters while providing better performance than HMMs in continuous state spaces. However, particle filters introduce their own computational challenges, particularly in high-dimensional spaces.
The integration of deep learning with both Kalman Filters and HMMs represents another frontier, with recurrent neural networks being used to learn system dynamics that traditional models struggle to capture. These hybrid approaches show promise but require significant expertise to implement effectively and lack the theoretical guarantees of their classical counterparts.
HMMs, conversely, have established dominance in speech recognition, natural language processing, and biological sequence analysis where discrete state transitions are prevalent. Recent advancements in variational inference methods have enhanced HMM training efficiency, while parallel computing architectures have mitigated some computational constraints.
A significant technical challenge for Kalman Filters remains their fundamental assumption of Gaussian noise distributions, which proves problematic in environments with multi-modal or heavy-tailed noise characteristics. Additionally, the linearization approximations in EKF can introduce substantial errors in highly nonlinear systems, potentially leading to filter divergence and prediction failures.
For HMMs, scalability presents a persistent challenge as state space dimensionality increases, with computational complexity growing exponentially. This "curse of dimensionality" limits practical application in high-dimensional systems without significant model simplification. Furthermore, HMMs struggle with long-range dependencies due to their Markov property assumption, which can be restrictive for complex sequential data.
Geographically, North American research institutions and technology companies lead in Kalman Filter innovations for autonomous systems, while European academic centers have contributed substantial theoretical advancements in HMM applications for natural language processing. Asian research groups, particularly in Japan and China, have made notable progress in hybrid approaches combining elements of both methodologies.
Recent research has focused on particle filters as an alternative that addresses limitations of both approaches, offering more flexible noise distribution handling than Kalman Filters while providing better performance than HMMs in continuous state spaces. However, particle filters introduce their own computational challenges, particularly in high-dimensional spaces.
The integration of deep learning with both Kalman Filters and HMMs represents another frontier, with recurrent neural networks being used to learn system dynamics that traditional models struggle to capture. These hybrid approaches show promise but require significant expertise to implement effectively and lack the theoretical guarantees of their classical counterparts.
Comparative Analysis of Implementation Approaches
01 Kalman Filter for Speech Recognition and Processing
Kalman filters are applied in speech recognition systems to improve prediction accuracy by filtering out noise and enhancing signal quality. These techniques help in tracking speech parameters over time, allowing for more accurate speech recognition in various environments. The implementation involves state estimation of speech signals, which leads to better recognition rates and more robust performance against background noise and distortions.- Kalman Filter for Speech Recognition and Processing: Kalman filters are applied in speech recognition systems to improve prediction accuracy by filtering out noise and enhancing signal quality. These techniques help in tracking speech parameters over time, allowing for more accurate speech recognition in various environments. The implementation involves state estimation of speech signals, which leads to better recognition rates and more robust performance against background noise and distortions.
- Hidden Markov Models for Pattern Recognition: Hidden Markov Models (HMMs) are utilized for pattern recognition tasks where sequential data needs to be analyzed. These models excel at capturing temporal dependencies in data, making them suitable for applications like handwriting recognition, gesture recognition, and anomaly detection. By modeling the probability distributions of state transitions and observations, HMMs can effectively predict future states based on current observations, improving overall prediction accuracy.
- Hybrid Systems Combining Kalman Filters and HMMs: Hybrid approaches that combine Kalman filters with Hidden Markov Models leverage the strengths of both techniques to achieve superior prediction accuracy. Kalman filters excel at handling continuous state estimation with Gaussian noise, while HMMs are effective for discrete state modeling. By integrating these methods, systems can better handle mixed continuous-discrete problems, resulting in more robust predictions across various domains including tracking, navigation, and signal processing.
- Machine Learning Enhancements for Prediction Models: Advanced machine learning techniques are being integrated with traditional Kalman filters and Hidden Markov Models to enhance prediction accuracy. These enhancements include deep learning approaches, neural networks, and adaptive algorithms that can automatically tune model parameters based on incoming data. Such integrations allow for more complex pattern recognition and improved handling of non-linear relationships, resulting in significant accuracy improvements for prediction tasks.
- Application-Specific Optimizations for Prediction Accuracy: Specialized implementations of Kalman filters and Hidden Markov Models are developed for specific application domains to maximize prediction accuracy. These optimizations include parameter tuning for particular use cases, domain-specific feature extraction, and customized state transition models. Applications range from healthcare monitoring and financial forecasting to autonomous navigation and industrial process control, each with tailored approaches to improve prediction performance.
02 Hidden Markov Models for Pattern Recognition
Hidden Markov Models (HMMs) are utilized for pattern recognition tasks, particularly in identifying sequential patterns in data. These models excel at capturing temporal dependencies and can predict future states based on current observations. The applications include gesture recognition, handwriting analysis, and other sequence-based pattern recognition tasks where the underlying states are not directly observable but can be inferred from the data.Expand Specific Solutions03 Hybrid Systems Combining Kalman Filters and HMMs
Hybrid approaches that combine Kalman filters with Hidden Markov Models leverage the strengths of both techniques to achieve superior prediction accuracy. Kalman filters provide optimal state estimation for linear systems with Gaussian noise, while HMMs handle sequential data with hidden states. This combination is particularly effective for complex systems where both continuous state estimation and discrete state transitions are important for accurate predictions.Expand Specific Solutions04 Machine Learning Enhancements for Prediction Models
Advanced machine learning techniques are used to enhance the prediction accuracy of both Kalman filters and Hidden Markov Models. These enhancements include neural network integration, deep learning approaches, and adaptive algorithms that can learn from new data. Such improvements allow the models to handle non-linear relationships and complex patterns more effectively, resulting in more accurate predictions across various applications.Expand Specific Solutions05 Real-time Applications and Performance Optimization
Implementation strategies for Kalman filters and Hidden Markov Models in real-time applications focus on optimizing computational efficiency while maintaining high prediction accuracy. These strategies include parallel processing, algorithm simplification, and hardware acceleration techniques. The optimization allows for deployment in resource-constrained environments such as mobile devices, embedded systems, and IoT applications where both speed and accuracy are critical.Expand Specific Solutions
Major Industry Players and Research Groups
The Kalman Filter vs Hidden Markov Models prediction technology landscape is currently in a mature development stage with established applications across multiple industries. The market size is expanding rapidly, driven by increasing demand for predictive analytics in autonomous systems, financial forecasting, and signal processing. From a technical maturity perspective, major players demonstrate varying specialization levels: Sony and Apple lead in consumer electronics applications, while Toshiba and Siemens Healthineers focus on industrial implementations. Academic institutions like Brown University and Wuhan University contribute significant research advancements. Boeing and Toyota leverage these technologies for navigation and control systems, while Applied Brain Research pioneers neuromorphic computing applications that enhance both approaches. BAE Systems and Schlumberger demonstrate specialized implementations in defense and energy sectors respectively.
Apple, Inc.
Technical Solution: Apple has developed advanced implementations of both Kalman Filters and Hidden Markov Models for various prediction tasks across its product ecosystem. For motion prediction and sensor fusion in devices like iPhone, Apple Watch, and AirPods, Apple employs Extended Kalman Filters (EKF) to combine data from accelerometers, gyroscopes, and magnetometers to accurately track movement and orientation. This approach enables features like spatial audio, fitness tracking, and gesture recognition. For voice recognition in Siri, Apple utilizes sophisticated Hidden Markov Models combined with deep learning techniques to model speech patterns and predict linguistic sequences. Apple's implementation focuses on on-device processing for enhanced privacy, with optimized algorithms that balance computational efficiency with prediction accuracy.
Strengths: Apple's implementations excel in real-time processing on resource-constrained mobile devices, with highly optimized algorithms that minimize battery consumption while maintaining accuracy. Their hybrid approaches combining traditional statistical methods with machine learning show excellent performance in noisy environments. Weaknesses: Apple's closed ecosystem limits cross-platform compatibility, and their proprietary implementations may sacrifice some flexibility for optimization within their specific hardware configurations.
The Boeing Co.
Technical Solution: Boeing has developed sophisticated prediction systems utilizing both Kalman Filters and Hidden Markov Models for aerospace applications. For flight control systems, Boeing implements Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) to estimate aircraft state parameters including position, velocity, attitude, and angular rates by fusing data from multiple sensors such as GPS, inertial measurement units, air data systems, and radar altimeters. This approach enables precise navigation even when individual sensors experience degraded performance or failure. For predictive maintenance applications, Boeing employs Hidden Markov Models to analyze patterns in sensor data from aircraft systems, modeling the progression of component degradation through discrete states. This allows maintenance teams to predict potential failures before they occur, optimizing maintenance schedules and reducing unplanned downtime. Boeing's implementation includes adaptive filtering techniques that automatically adjust model parameters based on flight conditions and sensor health status.
Strengths: Boeing's implementations demonstrate exceptional reliability in safety-critical applications with redundant systems architecture that maintains performance even during partial system failures. Their algorithms have been extensively validated through millions of flight hours across diverse operating conditions. Weaknesses: The high computational requirements of Boeing's sophisticated prediction models necessitate dedicated processing hardware, increasing system complexity and cost. Additionally, the models require extensive calibration and validation for each aircraft type, limiting rapid deployment across diverse platforms.
Technical Deep Dive: Core Algorithms and Mathematics
Forecasting apparatus, forecasting method, and storage medium
PatentPendingUS20230229980A1
Innovation
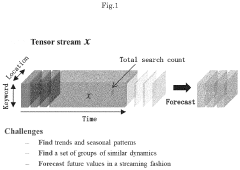
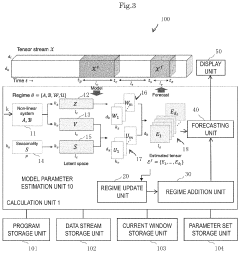
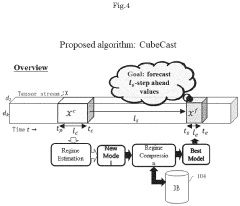
- The proposed forecasting apparatus, CubeCast, employs a non-linear transformation unit to capture trends and a linear transformation unit to capture seasonal intensity, using observation matrices to reproduce estimated data, which are then combined for accurate forecasting, and includes a regime update unit to adapt to changes in patterns over time, leveraging an adaptive non-linear dynamical system and minimum description length principle for model optimization.
Passive RF, single fighter aircraft multifunction aperture sensor, air to air geolocation
PatentInactiveUS7132961B2
Innovation
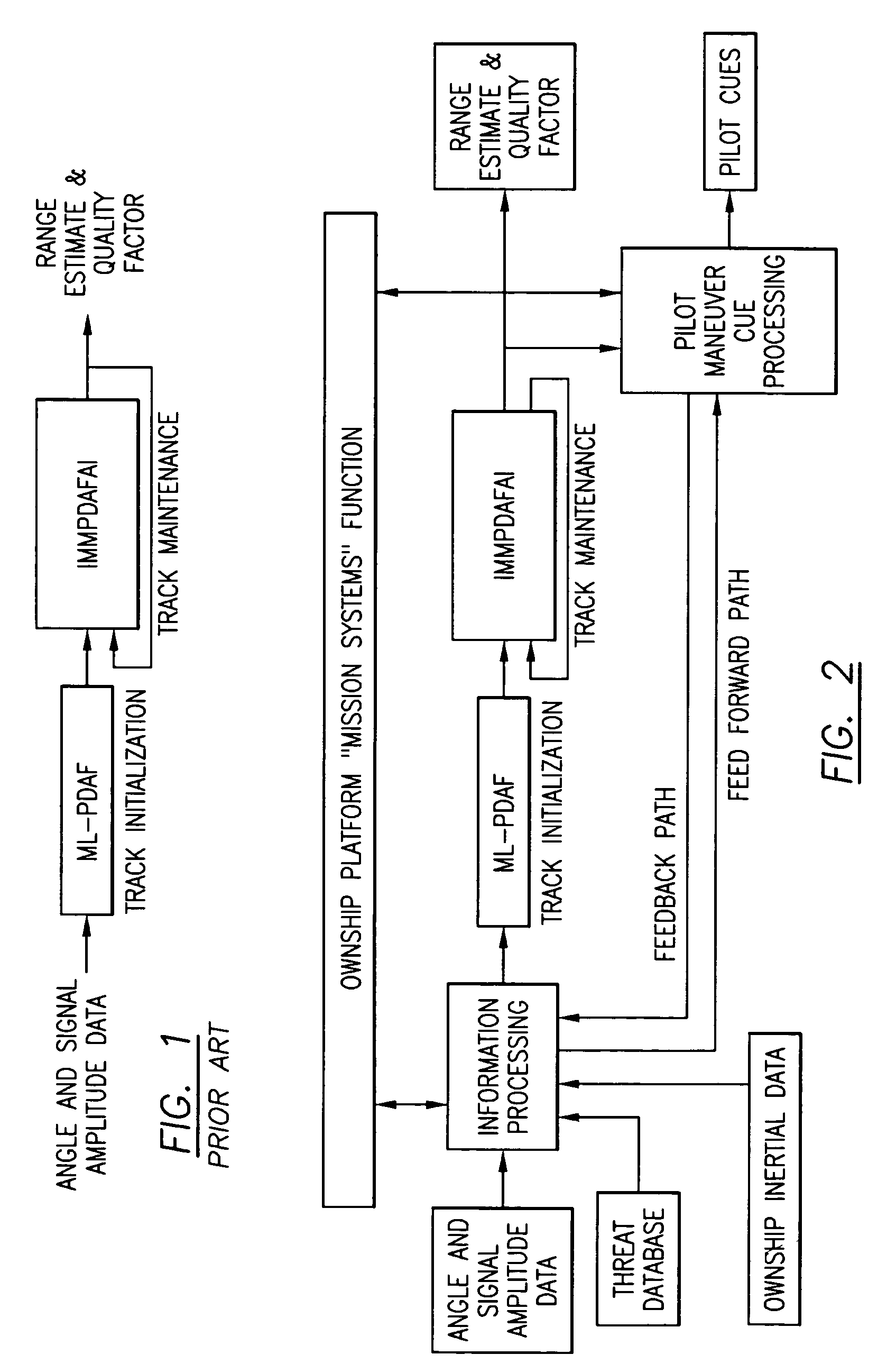
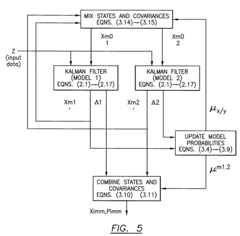
- The implementation of a method and system utilizing batch maximum likelihood (ML) and probabilistic data association filter (PDAF) methodologies, combined with recursive interacting multiple model (IMM) algorithms, which process noisy electronic warfare data, interferometer measurements, and real-time mission constraints to enhance passive range estimates and track maintenance.
Computational Efficiency and Performance Metrics
When comparing Kalman Filters and Hidden Markov Models (HMMs) for prediction tasks, computational efficiency and performance metrics represent critical factors that determine their practical applicability in real-world systems.
Kalman Filters demonstrate superior computational efficiency for continuous state estimation problems. Their recursive nature eliminates the need to store historical data, requiring only the previous state estimate and covariance matrix. The computational complexity scales linearly with the state dimension (O(n³) for n-dimensional state vectors), making them particularly efficient for low to moderate dimensional problems. In real-time applications such as navigation systems and robotics, Kalman Filters can process measurements at rates exceeding 1000Hz on standard hardware.
HMMs, conversely, exhibit higher computational demands due to their discrete state representation and the forward-backward algorithm. For an HMM with N states and T time steps, the standard Viterbi algorithm for state sequence prediction has O(N²T) complexity. This quadratic scaling with state space size can become prohibitive for problems with large state spaces, often requiring approximation techniques or hardware acceleration.
Performance metrics for these algorithms differ significantly based on application context. Kalman Filters are typically evaluated using Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and innovation consistency measures. They excel in tracking applications, achieving sub-meter accuracy in GPS-denied environments and maintaining consistent estimation error bounds when model assumptions are met.
HMMs are commonly assessed using prediction accuracy, F1-score, and log-likelihood metrics. They demonstrate particular strength in pattern recognition tasks, achieving recognition rates exceeding 95% in speech recognition applications and robust performance in biological sequence analysis.
Memory utilization presents another important distinction. Kalman Filters maintain constant memory requirements regardless of operation duration, typically requiring only O(n²) storage for an n-dimensional state. HMMs, however, may require O(NT) memory for full sequence analysis, though forward-only implementations can reduce this to O(N).
Convergence characteristics also differ substantially. Kalman Filters can adapt rapidly to new measurements, typically converging within 5-10 iterations in well-conditioned systems. HMMs require sufficient training data to accurately estimate transition and emission probabilities, with convergence of the Baum-Welch algorithm potentially requiring hundreds of iterations for complex models.
These efficiency and performance considerations directly impact implementation decisions across domains ranging from autonomous vehicles to financial forecasting, with hybrid approaches increasingly being developed to leverage the complementary strengths of both methodologies.
Kalman Filters demonstrate superior computational efficiency for continuous state estimation problems. Their recursive nature eliminates the need to store historical data, requiring only the previous state estimate and covariance matrix. The computational complexity scales linearly with the state dimension (O(n³) for n-dimensional state vectors), making them particularly efficient for low to moderate dimensional problems. In real-time applications such as navigation systems and robotics, Kalman Filters can process measurements at rates exceeding 1000Hz on standard hardware.
HMMs, conversely, exhibit higher computational demands due to their discrete state representation and the forward-backward algorithm. For an HMM with N states and T time steps, the standard Viterbi algorithm for state sequence prediction has O(N²T) complexity. This quadratic scaling with state space size can become prohibitive for problems with large state spaces, often requiring approximation techniques or hardware acceleration.
Performance metrics for these algorithms differ significantly based on application context. Kalman Filters are typically evaluated using Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and innovation consistency measures. They excel in tracking applications, achieving sub-meter accuracy in GPS-denied environments and maintaining consistent estimation error bounds when model assumptions are met.
HMMs are commonly assessed using prediction accuracy, F1-score, and log-likelihood metrics. They demonstrate particular strength in pattern recognition tasks, achieving recognition rates exceeding 95% in speech recognition applications and robust performance in biological sequence analysis.
Memory utilization presents another important distinction. Kalman Filters maintain constant memory requirements regardless of operation duration, typically requiring only O(n²) storage for an n-dimensional state. HMMs, however, may require O(NT) memory for full sequence analysis, though forward-only implementations can reduce this to O(N).
Convergence characteristics also differ substantially. Kalman Filters can adapt rapidly to new measurements, typically converging within 5-10 iterations in well-conditioned systems. HMMs require sufficient training data to accurately estimate transition and emission probabilities, with convergence of the Baum-Welch algorithm potentially requiring hundreds of iterations for complex models.
These efficiency and performance considerations directly impact implementation decisions across domains ranging from autonomous vehicles to financial forecasting, with hybrid approaches increasingly being developed to leverage the complementary strengths of both methodologies.
Real-world Case Studies and Implementation Examples
In the autonomous vehicle industry, Kalman Filters have demonstrated remarkable success in sensor fusion applications. Tesla's Autopilot system utilizes Extended Kalman Filters to combine data from cameras, radar, and ultrasonic sensors, enabling accurate vehicle positioning even when GPS signals are compromised. The implementation allows for real-time tracking with computational efficiency critical for embedded systems with limited processing power.
Similarly, Waymo's self-driving technology employs Unscented Kalman Filters to handle the non-linearities inherent in vehicle dynamics, achieving positioning accuracy within centimeters. This precision is essential for navigating complex urban environments and making split-second driving decisions.
Hidden Markov Models have found their niche in different prediction scenarios. Google's speech recognition system leverages HMMs to model the sequential nature of speech patterns, enabling accurate transcription across various accents and speaking styles. The implementation processes audio signals as observation sequences and maps them to probable word sequences, demonstrating HMMs' strength in handling sequential data with inherent uncertainty.
In financial markets, JPMorgan Chase employs HMMs for regime detection in market behavior, identifying bull, bear, and sideways markets as hidden states while using price movements as observations. This implementation helps optimize trading strategies based on the detected market regime, showcasing HMMs' ability to uncover latent patterns in time series data.
Weather forecasting systems by the European Centre for Medium-Range Weather Forecasts utilize Ensemble Kalman Filters to assimilate meteorological observations into numerical weather prediction models. This implementation handles the high-dimensional state spaces characteristic of atmospheric systems, demonstrating Kalman Filters' scalability to complex physical models.
In robotics, Boston Dynamics' robots implement Kalman Filters for state estimation during dynamic movements. The filter's predictive capabilities enable the robots to maintain balance even when subjected to unexpected external forces, highlighting the Kalman Filter's strength in systems where physical models are well-understood.
Netflix's recommendation system incorporates HMMs to model user viewing behavior over time, capturing the temporal dependencies in content consumption patterns. This implementation helps predict not just what content users might enjoy, but when they are likely to watch different types of content, showcasing HMMs' ability to model sequential decision processes.
Similarly, Waymo's self-driving technology employs Unscented Kalman Filters to handle the non-linearities inherent in vehicle dynamics, achieving positioning accuracy within centimeters. This precision is essential for navigating complex urban environments and making split-second driving decisions.
Hidden Markov Models have found their niche in different prediction scenarios. Google's speech recognition system leverages HMMs to model the sequential nature of speech patterns, enabling accurate transcription across various accents and speaking styles. The implementation processes audio signals as observation sequences and maps them to probable word sequences, demonstrating HMMs' strength in handling sequential data with inherent uncertainty.
In financial markets, JPMorgan Chase employs HMMs for regime detection in market behavior, identifying bull, bear, and sideways markets as hidden states while using price movements as observations. This implementation helps optimize trading strategies based on the detected market regime, showcasing HMMs' ability to uncover latent patterns in time series data.
Weather forecasting systems by the European Centre for Medium-Range Weather Forecasts utilize Ensemble Kalman Filters to assimilate meteorological observations into numerical weather prediction models. This implementation handles the high-dimensional state spaces characteristic of atmospheric systems, demonstrating Kalman Filters' scalability to complex physical models.
In robotics, Boston Dynamics' robots implement Kalman Filters for state estimation during dynamic movements. The filter's predictive capabilities enable the robots to maintain balance even when subjected to unexpected external forces, highlighting the Kalman Filter's strength in systems where physical models are well-understood.
Netflix's recommendation system incorporates HMMs to model user viewing behavior over time, capturing the temporal dependencies in content consumption patterns. This implementation helps predict not just what content users might enjoy, but when they are likely to watch different types of content, showcasing HMMs' ability to model sequential decision processes.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!