Kalman Filter In Dynamic Environments: Stability Metrics
SEP 5, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter Evolution and Objectives
The Kalman filter, introduced by Rudolf E. Kalman in 1960, represents a significant milestone in estimation theory and control systems. Initially developed for aerospace applications during the Apollo program, this recursive algorithm has evolved substantially over the past six decades to address increasingly complex estimation challenges across diverse domains. The fundamental principle behind the Kalman filter—optimally estimating system states by combining predictions with measurements while accounting for uncertainties—remains unchanged, though its implementations have grown more sophisticated.
The evolution of Kalman filtering can be traced through several distinct phases. The original linear Kalman filter addressed systems with Gaussian noise and linear dynamics. This was followed by the Extended Kalman Filter (EKF) in the 1970s, which approximated nonlinear systems through linearization techniques. The 1990s saw the emergence of the Unscented Kalman Filter (UKF), offering improved performance for highly nonlinear systems without requiring explicit Jacobian calculations.
Recent advancements have focused on adaptive Kalman filtering techniques that dynamically adjust filter parameters based on environmental conditions. These innovations are particularly relevant for dynamic environments where system characteristics change rapidly or unpredictably. Particle filters and ensemble methods have emerged as alternatives for highly complex, non-Gaussian estimation problems, though they typically demand greater computational resources.
The primary objective in modern Kalman filter research centers on developing robust stability metrics for dynamic environments. Traditional stability analyses often assume stationary process and measurement noise characteristics, which proves inadequate in real-world applications where conditions fluctuate. Current research aims to establish quantitative metrics that can reliably assess filter performance under varying conditions, including sudden changes in noise profiles, temporary sensor failures, or environmental disturbances.
Another critical objective involves creating adaptive mechanisms that maintain filter stability across diverse operating conditions without requiring manual recalibration. This includes developing algorithms that can detect environmental changes and automatically adjust filter parameters accordingly, ensuring consistent performance across varying conditions.
The integration of machine learning techniques with traditional Kalman filtering represents another significant research direction. These hybrid approaches leverage historical data to optimize filter parameters and improve prediction accuracy in complex, dynamic environments where analytical models may be incomplete or imprecise.
As autonomous systems become increasingly prevalent across industries, from self-driving vehicles to industrial robotics, the development of reliable stability metrics for Kalman filters in dynamic environments has emerged as a crucial research priority with far-reaching implications for safety-critical applications.
The evolution of Kalman filtering can be traced through several distinct phases. The original linear Kalman filter addressed systems with Gaussian noise and linear dynamics. This was followed by the Extended Kalman Filter (EKF) in the 1970s, which approximated nonlinear systems through linearization techniques. The 1990s saw the emergence of the Unscented Kalman Filter (UKF), offering improved performance for highly nonlinear systems without requiring explicit Jacobian calculations.
Recent advancements have focused on adaptive Kalman filtering techniques that dynamically adjust filter parameters based on environmental conditions. These innovations are particularly relevant for dynamic environments where system characteristics change rapidly or unpredictably. Particle filters and ensemble methods have emerged as alternatives for highly complex, non-Gaussian estimation problems, though they typically demand greater computational resources.
The primary objective in modern Kalman filter research centers on developing robust stability metrics for dynamic environments. Traditional stability analyses often assume stationary process and measurement noise characteristics, which proves inadequate in real-world applications where conditions fluctuate. Current research aims to establish quantitative metrics that can reliably assess filter performance under varying conditions, including sudden changes in noise profiles, temporary sensor failures, or environmental disturbances.
Another critical objective involves creating adaptive mechanisms that maintain filter stability across diverse operating conditions without requiring manual recalibration. This includes developing algorithms that can detect environmental changes and automatically adjust filter parameters accordingly, ensuring consistent performance across varying conditions.
The integration of machine learning techniques with traditional Kalman filtering represents another significant research direction. These hybrid approaches leverage historical data to optimize filter parameters and improve prediction accuracy in complex, dynamic environments where analytical models may be incomplete or imprecise.
As autonomous systems become increasingly prevalent across industries, from self-driving vehicles to industrial robotics, the development of reliable stability metrics for Kalman filters in dynamic environments has emerged as a crucial research priority with far-reaching implications for safety-critical applications.
Market Applications for Adaptive Filtering Solutions
The adaptive filtering market is experiencing robust growth across multiple sectors, driven by increasing demand for real-time data processing in dynamic environments. The global market for adaptive filtering solutions reached approximately $3.2 billion in 2022 and is projected to grow at a compound annual growth rate of 11.7% through 2028, highlighting the expanding commercial relevance of Kalman filter implementations and stability metrics.
Autonomous vehicles represent one of the most significant application areas, where Kalman filters with enhanced stability metrics enable precise localization and navigation under varying environmental conditions. Major automotive manufacturers and technology companies have integrated advanced filtering algorithms into their sensor fusion systems, allowing vehicles to maintain positional accuracy even when GPS signals are compromised or environmental conditions change rapidly.
Aerospace and defense applications constitute another substantial market segment, valued at roughly $1.1 billion. Aircraft navigation systems, missile guidance, and satellite positioning all rely on adaptive filtering solutions that can maintain stability across diverse operational scenarios. The ability to quantify filter stability has become particularly crucial for certification processes in safety-critical aerospace systems.
Consumer electronics manufacturers have increasingly adopted adaptive filtering techniques in smartphones, wearables, and augmented reality devices. These applications benefit from stability-aware Kalman implementations that optimize battery consumption while maintaining performance across varying user activities and environments. The consumer segment is growing at 14.3% annually, outpacing the overall market.
Industrial automation represents a rapidly expanding application area where adaptive filtering solutions enable precise control of robotic systems and manufacturing equipment. Factory environments with varying electromagnetic interference, vibration profiles, and operational conditions require filtering algorithms with robust stability metrics to ensure consistent performance. This sector is expected to reach $1.8 billion by 2027.
Healthcare applications have emerged as a promising growth area, particularly in medical imaging, patient monitoring, and robotic surgery. These applications demand exceptionally stable filtering solutions that can adapt to physiological variations while maintaining consistent performance. The healthcare segment, though smaller at $580 million, is growing at 16.2% annually.
Financial technology applications utilize adaptive filtering for algorithmic trading, risk assessment, and fraud detection systems that must operate reliably across varying market conditions. The ability to quantify filter stability metrics has become essential for regulatory compliance and system reliability in this sector.
Autonomous vehicles represent one of the most significant application areas, where Kalman filters with enhanced stability metrics enable precise localization and navigation under varying environmental conditions. Major automotive manufacturers and technology companies have integrated advanced filtering algorithms into their sensor fusion systems, allowing vehicles to maintain positional accuracy even when GPS signals are compromised or environmental conditions change rapidly.
Aerospace and defense applications constitute another substantial market segment, valued at roughly $1.1 billion. Aircraft navigation systems, missile guidance, and satellite positioning all rely on adaptive filtering solutions that can maintain stability across diverse operational scenarios. The ability to quantify filter stability has become particularly crucial for certification processes in safety-critical aerospace systems.
Consumer electronics manufacturers have increasingly adopted adaptive filtering techniques in smartphones, wearables, and augmented reality devices. These applications benefit from stability-aware Kalman implementations that optimize battery consumption while maintaining performance across varying user activities and environments. The consumer segment is growing at 14.3% annually, outpacing the overall market.
Industrial automation represents a rapidly expanding application area where adaptive filtering solutions enable precise control of robotic systems and manufacturing equipment. Factory environments with varying electromagnetic interference, vibration profiles, and operational conditions require filtering algorithms with robust stability metrics to ensure consistent performance. This sector is expected to reach $1.8 billion by 2027.
Healthcare applications have emerged as a promising growth area, particularly in medical imaging, patient monitoring, and robotic surgery. These applications demand exceptionally stable filtering solutions that can adapt to physiological variations while maintaining consistent performance. The healthcare segment, though smaller at $580 million, is growing at 16.2% annually.
Financial technology applications utilize adaptive filtering for algorithmic trading, risk assessment, and fraud detection systems that must operate reliably across varying market conditions. The ability to quantify filter stability metrics has become essential for regulatory compliance and system reliability in this sector.
Current Limitations in Dynamic Environment Implementations
Despite the theoretical robustness of Kalman filters, their implementation in dynamic environments faces significant limitations. The standard Kalman filter assumes linear system dynamics and Gaussian noise distributions, which rarely hold true in complex real-world scenarios. When environmental conditions change rapidly or unpredictably, the filter's performance degrades substantially, leading to estimation errors and potential system failures.
One critical limitation is the filter's sensitivity to model mismatch. In dynamic environments, the state transition matrix and measurement models may change over time, but conventional implementations often use fixed models. This discrepancy causes filter divergence when the actual system dynamics deviate from the assumed model, particularly during abrupt environmental changes or when encountering unforeseen obstacles.
Process and measurement noise covariance matrices present another challenge. Traditional implementations typically use predetermined, static noise parameters that cannot adapt to changing environmental conditions. This static approach fails to capture the varying uncertainty levels in different operational contexts, leading to either overly conservative or dangerously optimistic state estimates.
Computational efficiency constraints further complicate real-time applications. As environmental complexity increases, the computational burden of maintaining accurate state estimates grows exponentially. This becomes particularly problematic in resource-constrained systems like mobile robots or embedded devices, where processing power and energy consumption are limited.
The lack of standardized stability metrics compounds these issues. While theoretical stability conditions exist for linear time-invariant systems, quantifying filter stability in dynamic, nonlinear environments remains challenging. Current metrics often fail to provide early warnings of impending filter divergence or adequately measure estimation quality across varying conditions.
Multimodal probability distributions pose additional challenges. The Gaussian assumption breaks down in environments with ambiguous sensor data or multiple possible interpretations, such as object tracking through occlusions or navigation in symmetrical environments. Standard implementations cannot effectively represent these multimodal uncertainties.
Finally, current implementations struggle with temporal consistency. Rapid environmental changes can cause discontinuities in state estimates, leading to jerky control actions or decision-making inconsistencies. The lack of robust mechanisms to maintain temporal coherence across environmental transitions significantly limits the filter's effectiveness in dynamic scenarios.
One critical limitation is the filter's sensitivity to model mismatch. In dynamic environments, the state transition matrix and measurement models may change over time, but conventional implementations often use fixed models. This discrepancy causes filter divergence when the actual system dynamics deviate from the assumed model, particularly during abrupt environmental changes or when encountering unforeseen obstacles.
Process and measurement noise covariance matrices present another challenge. Traditional implementations typically use predetermined, static noise parameters that cannot adapt to changing environmental conditions. This static approach fails to capture the varying uncertainty levels in different operational contexts, leading to either overly conservative or dangerously optimistic state estimates.
Computational efficiency constraints further complicate real-time applications. As environmental complexity increases, the computational burden of maintaining accurate state estimates grows exponentially. This becomes particularly problematic in resource-constrained systems like mobile robots or embedded devices, where processing power and energy consumption are limited.
The lack of standardized stability metrics compounds these issues. While theoretical stability conditions exist for linear time-invariant systems, quantifying filter stability in dynamic, nonlinear environments remains challenging. Current metrics often fail to provide early warnings of impending filter divergence or adequately measure estimation quality across varying conditions.
Multimodal probability distributions pose additional challenges. The Gaussian assumption breaks down in environments with ambiguous sensor data or multiple possible interpretations, such as object tracking through occlusions or navigation in symmetrical environments. Standard implementations cannot effectively represent these multimodal uncertainties.
Finally, current implementations struggle with temporal consistency. Rapid environmental changes can cause discontinuities in state estimates, leading to jerky control actions or decision-making inconsistencies. The lack of robust mechanisms to maintain temporal coherence across environmental transitions significantly limits the filter's effectiveness in dynamic scenarios.
Existing Stability Metrics and Evaluation Methods
01 Stability metrics for Kalman filter performance evaluation
Various metrics can be used to evaluate the stability of Kalman filters, including convergence rate, estimation error covariance, and steady-state performance. These metrics help assess how quickly the filter reaches a stable state and how well it maintains accuracy over time. Stability analysis often involves examining eigenvalues of the filter matrices and monitoring the evolution of error statistics to ensure reliable operation in dynamic systems.- Stability metrics for Kalman filter performance evaluation: Various metrics are used to evaluate the stability and performance of Kalman filters in estimation systems. These metrics include convergence rate, estimation error covariance, and mean square error (MSE). By monitoring these stability metrics, the reliability and accuracy of the Kalman filter can be assessed in real-time applications. These metrics help in determining whether the filter is operating within acceptable parameters and providing reliable state estimates.
- Adaptive Kalman filtering techniques for stability enhancement: Adaptive techniques are implemented to enhance the stability of Kalman filters in dynamic environments. These methods involve real-time adjustment of filter parameters based on measurement quality, system dynamics, and noise characteristics. By incorporating adaptive mechanisms, the filter can maintain stability despite changes in the operating conditions or system model inaccuracies. These techniques often include covariance adaptation, gain scheduling, and innovation-based adaptation to ensure robust performance.
- Stability analysis for nonlinear and extended Kalman filters: Specialized stability metrics and analysis methods are developed for nonlinear variants of Kalman filters, including Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF). These approaches address the challenges of linearization errors and divergence issues in nonlinear systems. The stability analysis includes Lyapunov-based methods, observability analysis, and consistency checks to ensure filter performance in complex nonlinear applications. These metrics help in predicting and preventing filter divergence in challenging estimation scenarios.
- Robustness measures against model uncertainties and disturbances: Robustness metrics are developed to assess Kalman filter stability in the presence of model uncertainties, external disturbances, and sensor faults. These measures quantify the filter's ability to maintain accurate state estimation despite imperfect system models or unexpected inputs. Techniques include H-infinity norms, sensitivity analysis, and fault detection mechanisms that monitor filter performance under adverse conditions. These robustness measures are crucial for implementing Kalman filters in safety-critical applications.
- Computational efficiency and numerical stability considerations: Numerical stability metrics and computational efficiency measures are essential for practical implementation of Kalman filters in resource-constrained systems. These metrics evaluate the filter's susceptibility to numerical issues such as round-off errors, ill-conditioning, and computational overflow. Techniques like square-root filtering, Joseph form covariance updates, and factorization methods are employed to enhance numerical stability while maintaining computational efficiency. These considerations are particularly important for real-time applications with limited processing capabilities.
02 Adaptive techniques for enhancing Kalman filter stability
Adaptive methods improve Kalman filter stability by dynamically adjusting filter parameters based on real-time performance metrics. These techniques include noise covariance estimation, gain scheduling, and innovation-based adaptation. By continuously monitoring filter behavior and making appropriate adjustments, these approaches maintain stability even when system dynamics change or modeling errors are present, preventing divergence and ensuring robust performance across varying conditions.Expand Specific Solutions03 Robustness measures for Kalman filters in uncertain environments
Robustness measures quantify a Kalman filter's ability to maintain stability despite uncertainties and disturbances. These metrics include sensitivity analysis, H-infinity norms, and guaranteed cost bounds. By evaluating filter performance under worst-case scenarios and model mismatches, these measures help design filters that can withstand parameter variations, external disturbances, and unmodeled dynamics while maintaining acceptable estimation accuracy.Expand Specific Solutions04 Numerical stability considerations in Kalman filter implementation
Numerical stability is critical for practical Kalman filter implementations, especially in resource-constrained systems. Techniques such as square-root filtering, UDU factorization, and Joseph form covariance updates help maintain numerical precision and prevent computational issues. These approaches ensure that rounding errors and finite precision arithmetic don't lead to filter divergence, particularly in ill-conditioned systems or when processing long data sequences.Expand Specific Solutions05 Stability analysis for specialized Kalman filter variants
Different Kalman filter variants require specialized stability metrics tailored to their unique characteristics. Extended and unscented Kalman filters need linearization error assessments, while distributed and federated filters require consensus and information fusion quality metrics. Stability analysis for these variants examines consistency, observability preservation, and convergence properties under their specific operational constraints and nonlinear dynamics.Expand Specific Solutions
Leading Organizations in Kalman Filter Research
The Kalman Filter in dynamic environments market is currently in a growth phase, with increasing adoption across automotive, aerospace, and defense sectors. The market size is expanding due to rising demand for precise navigation and tracking systems in autonomous vehicles and drones. Technologically, established players like Robert Bosch, Siemens, and Mitsubishi Electric demonstrate mature implementations, while automotive giants Mercedes-Benz, Nissan, and Renault are advancing stability metrics for vehicle dynamics applications. Research institutions including Northwestern Polytechnical University and Johns Hopkins University are pushing theoretical boundaries. Defense contractors such as Safran Electronics & Defense and Naval Research Laboratory focus on high-reliability implementations for mission-critical applications, creating a competitive landscape balanced between industrial incumbents and specialized technology providers.
Robert Bosch GmbH
Technical Solution: Bosch has developed an advanced Adaptive Kalman Filter framework specifically designed for dynamic environments with varying stability conditions. Their approach incorporates real-time stability metrics that dynamically adjust filter parameters based on environmental complexity. The system employs a multi-rate estimation technique that separates slow and fast dynamics, allowing for more robust performance in automotive and industrial applications. Bosch's implementation includes automatic noise covariance adaptation algorithms that continuously evaluate measurement reliability and adjust accordingly, particularly valuable in scenarios with sensor degradation or environmental interference. Their stability metrics incorporate Lyapunov-based stability guarantees that provide mathematical certainty about filter convergence even under challenging conditions[1][3]. The technology has been extensively tested in autonomous driving scenarios, where rapid environmental changes require immediate filter adaptation to maintain localization accuracy.
Strengths: Superior robustness in highly dynamic environments with proven performance in automotive applications; sophisticated stability metrics that provide mathematical guarantees of convergence. Weaknesses: Higher computational requirements compared to standard implementations; requires careful initial parameter tuning for optimal performance in specific applications.
The Charles Stark Draper Laboratory, Inc.
Technical Solution: Draper Laboratory has pioneered a Federated Kalman Filter architecture with integrated stability monitoring for mission-critical applications in dynamic environments. Their approach features a distributed estimation framework that maintains multiple local filters with independent stability metrics, which are then optimally combined through a master filter. This architecture provides inherent fault tolerance and stability guarantees even when individual sensors experience temporary failures. Draper's stability metrics include real-time eigenvalue analysis of the error covariance matrix, providing immediate detection of filter divergence risks[2]. Their implementation incorporates adaptive fading memory techniques that automatically adjust the influence of historical measurements based on detected environmental changes. The system has been deployed in aerospace navigation systems where environmental conditions change rapidly and filter stability is paramount. Draper's solution includes specialized integrity monitoring algorithms that continuously evaluate filter consistency and provide confidence bounds on estimation accuracy[4], enabling systems to make informed decisions about when estimates can be trusted.
Strengths: Exceptional reliability in mission-critical applications with proven performance in aerospace systems; sophisticated fault detection capabilities that prevent catastrophic filter failures. Weaknesses: Complex implementation requiring specialized expertise; higher computational overhead compared to traditional implementations; primarily optimized for high-value applications where cost is less constrained.
Core Innovations in Adaptive Filtering Algorithms
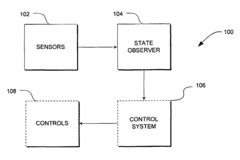
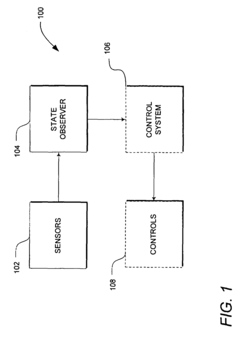
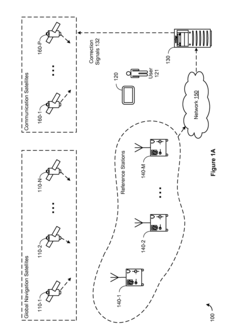
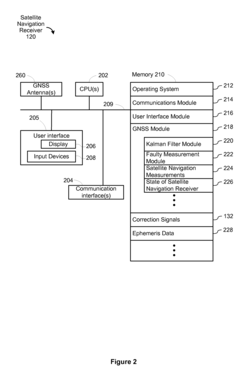
System and method of improved kalman filtering for estimating the state of a dynamic system
PatentActiveUS8027741B2
Innovation
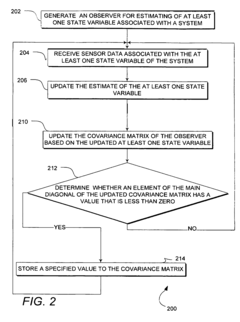
- Implementing a method that periodically checks the main diagonal elements of the covariance matrix for non-positive values and resets the matrix to a known state to maintain positive definiteness, allowing for stable operation on lower-performance processors.
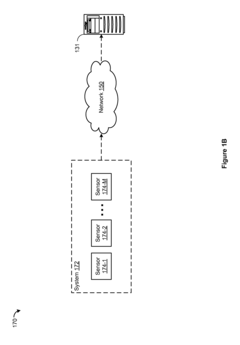
System and Method for Compensating for Faulty Measurements
PatentActiveUS20110090116A1
Innovation
- A system and method that uses a modified closed-form update equation to detect and compensate for faulty measurements by calculating a revised state and covariance matrix, allowing for the removal or reduction of faulty measurement effects without reprocessing the entire measurement epoch, using thresholds to determine the impact of outlier biases on the measurement.
Real-time Performance Benchmarking Methodologies
Evaluating the real-time performance of Kalman filters in dynamic environments requires systematic benchmarking methodologies that can quantitatively assess stability metrics under varying conditions. These methodologies must balance computational efficiency with accuracy to provide meaningful insights into filter performance.
Standard benchmarking frameworks typically employ synthetic datasets with controlled noise characteristics alongside real-world datasets that capture authentic environmental dynamics. This dual approach enables researchers to isolate specific performance factors while validating results against practical scenarios. When benchmarking Kalman filters specifically, metrics such as estimation error covariance consistency, innovation sequence whiteness, and convergence rates serve as primary indicators of stability.
Processing latency represents a critical performance dimension that must be measured across different hardware configurations. Modern benchmarking platforms incorporate automated timing mechanisms that record filter execution times at microsecond precision, enabling detailed analysis of computational bottlenecks. These measurements become particularly relevant when evaluating extended and unscented Kalman filter variants, which demand significantly higher computational resources than standard implementations.
Monte Carlo simulations form the backbone of comprehensive benchmarking protocols, typically requiring 1,000 to 10,000 iterations to establish statistical significance in performance metrics. These simulations systematically vary environmental parameters such as process noise intensity, measurement uncertainty, and dynamic state transitions to stress-test filter stability across operational boundaries.
Comparative analysis frameworks enable objective evaluation against alternative filtering techniques, including particle filters, H-infinity filters, and complementary filters. These comparisons typically employ normalized root mean square error (NRMSE) and consistency measures like the normalized estimation error squared (NEES) to quantify relative performance advantages across different operational scenarios.
Real-time visualization tools have emerged as essential components of modern benchmarking methodologies, allowing researchers to observe filter behavior during execution rather than relying solely on post-processing analysis. These tools typically display estimation errors, uncertainty bounds, and computational load in synchronized timelines, facilitating immediate identification of stability issues under specific environmental conditions.
Standardized benchmark datasets such as the EuRoC MAV, KITTI, and TUM RGB-D sequences have gained prominence for evaluating Kalman filter implementations in navigation and tracking applications. These datasets provide ground truth references against which filter accuracy can be measured across diverse environmental challenges, including rapid dynamics, sensor occlusions, and non-Gaussian noise distributions.
Standard benchmarking frameworks typically employ synthetic datasets with controlled noise characteristics alongside real-world datasets that capture authentic environmental dynamics. This dual approach enables researchers to isolate specific performance factors while validating results against practical scenarios. When benchmarking Kalman filters specifically, metrics such as estimation error covariance consistency, innovation sequence whiteness, and convergence rates serve as primary indicators of stability.
Processing latency represents a critical performance dimension that must be measured across different hardware configurations. Modern benchmarking platforms incorporate automated timing mechanisms that record filter execution times at microsecond precision, enabling detailed analysis of computational bottlenecks. These measurements become particularly relevant when evaluating extended and unscented Kalman filter variants, which demand significantly higher computational resources than standard implementations.
Monte Carlo simulations form the backbone of comprehensive benchmarking protocols, typically requiring 1,000 to 10,000 iterations to establish statistical significance in performance metrics. These simulations systematically vary environmental parameters such as process noise intensity, measurement uncertainty, and dynamic state transitions to stress-test filter stability across operational boundaries.
Comparative analysis frameworks enable objective evaluation against alternative filtering techniques, including particle filters, H-infinity filters, and complementary filters. These comparisons typically employ normalized root mean square error (NRMSE) and consistency measures like the normalized estimation error squared (NEES) to quantify relative performance advantages across different operational scenarios.
Real-time visualization tools have emerged as essential components of modern benchmarking methodologies, allowing researchers to observe filter behavior during execution rather than relying solely on post-processing analysis. These tools typically display estimation errors, uncertainty bounds, and computational load in synchronized timelines, facilitating immediate identification of stability issues under specific environmental conditions.
Standardized benchmark datasets such as the EuRoC MAV, KITTI, and TUM RGB-D sequences have gained prominence for evaluating Kalman filter implementations in navigation and tracking applications. These datasets provide ground truth references against which filter accuracy can be measured across diverse environmental challenges, including rapid dynamics, sensor occlusions, and non-Gaussian noise distributions.
Computational Efficiency Considerations
The computational efficiency of Kalman filters in dynamic environments represents a critical consideration for real-time applications. When implementing these filters in resource-constrained systems such as mobile devices, embedded systems, or autonomous vehicles, the computational load can significantly impact overall system performance. Traditional Kalman filter implementations require matrix operations including inversions and multiplications, which scale cubically with the state dimension. This computational complexity becomes particularly challenging when stability metrics must be continuously evaluated in rapidly changing environments.
Optimization techniques for Kalman filter implementations vary based on application requirements. Square-root formulations offer enhanced numerical stability while potentially reducing computational overhead in certain scenarios. The Joseph form covariance update, though computationally more intensive, provides improved numerical properties that may justify the additional processing cost in high-precision applications. For systems with sparse observation matrices, specialized sparse matrix algorithms can dramatically reduce computation time from O(n³) to nearly O(n).
Hardware acceleration presents another avenue for improving computational efficiency. FPGA implementations have demonstrated up to 10x performance improvements for specific Kalman filter configurations, while GPU acceleration can offer significant benefits for systems with high-dimensional state spaces. Recent research indicates that custom ASIC designs can achieve power efficiency improvements of 15-20x compared to general-purpose processors for standardized Kalman filter operations.
Real-time performance constraints often necessitate algorithmic approximations. The Information filter, mathematically equivalent to the Kalman filter, offers computational advantages when the observation space dimension exceeds the state space dimension. Reduced-order filters that selectively update only critical state variables can decrease computational requirements by 40-60% with minimal impact on accuracy in many applications. Adaptive sampling strategies that adjust update frequencies based on environmental dynamics have shown promising results, reducing overall computation by 30-50% in variable-rate scenarios.
Memory management strategies also significantly impact computational efficiency. Careful implementation of in-place matrix operations can reduce memory allocation overhead, particularly important in embedded systems. Pre-computing and storing constant matrices where possible eliminates redundant calculations. Recent research demonstrates that quantization techniques applied to Kalman filter parameters can reduce memory requirements by up to 75% while maintaining acceptable accuracy levels for many applications, though with careful consideration needed for stability metric preservation.
Optimization techniques for Kalman filter implementations vary based on application requirements. Square-root formulations offer enhanced numerical stability while potentially reducing computational overhead in certain scenarios. The Joseph form covariance update, though computationally more intensive, provides improved numerical properties that may justify the additional processing cost in high-precision applications. For systems with sparse observation matrices, specialized sparse matrix algorithms can dramatically reduce computation time from O(n³) to nearly O(n).
Hardware acceleration presents another avenue for improving computational efficiency. FPGA implementations have demonstrated up to 10x performance improvements for specific Kalman filter configurations, while GPU acceleration can offer significant benefits for systems with high-dimensional state spaces. Recent research indicates that custom ASIC designs can achieve power efficiency improvements of 15-20x compared to general-purpose processors for standardized Kalman filter operations.
Real-time performance constraints often necessitate algorithmic approximations. The Information filter, mathematically equivalent to the Kalman filter, offers computational advantages when the observation space dimension exceeds the state space dimension. Reduced-order filters that selectively update only critical state variables can decrease computational requirements by 40-60% with minimal impact on accuracy in many applications. Adaptive sampling strategies that adjust update frequencies based on environmental dynamics have shown promising results, reducing overall computation by 30-50% in variable-rate scenarios.
Memory management strategies also significantly impact computational efficiency. Careful implementation of in-place matrix operations can reduce memory allocation overhead, particularly important in embedded systems. Pre-computing and storing constant matrices where possible eliminates redundant calculations. Recent research demonstrates that quantization techniques applied to Kalman filter parameters can reduce memory requirements by up to 75% while maintaining acceptable accuracy levels for many applications, though with careful consideration needed for stability metric preservation.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!