How To Apply Kalman Filter In Optical Flow Analysis
SEP 12, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter in Optical Flow: Background and Objectives
Optical flow analysis has evolved significantly since its inception in the 1980s, becoming a cornerstone technique in computer vision for estimating motion between consecutive frames. The integration of Kalman filtering with optical flow represents a critical advancement in this domain, combining the strengths of both methodologies to enhance motion tracking accuracy and robustness in dynamic environments.
The historical development of optical flow began with the seminal work of Horn and Schunck, who introduced the concept of brightness constancy as a fundamental assumption. This was followed by Lucas-Kanade's local method, which improved computational efficiency but struggled with noise sensitivity. The technological trajectory has since moved toward more sophisticated approaches that can handle complex scenarios involving occlusions, illumination changes, and non-rigid motion patterns.
Kalman filtering, originally developed for aerospace applications in the 1960s, has found its way into computer vision due to its powerful state estimation capabilities under uncertainty. The filter's recursive nature makes it particularly suitable for real-time applications where computational resources are limited, yet precision remains paramount.
The convergence of these two technologies addresses several persistent challenges in motion analysis. Traditional optical flow methods often suffer from accumulating errors and sensitivity to noise, while Kalman filters excel at providing statistically optimal estimates by balancing measurement uncertainty with motion dynamics modeling.
Current research trends indicate a growing interest in applying these combined techniques across diverse fields including autonomous vehicles, robotics, surveillance systems, and medical imaging. The integration aims to achieve more accurate trajectory predictions, improved object tracking in cluttered environments, and enhanced stability in the presence of sensor noise or temporary occlusions.
The primary technical objectives for Kalman filter application in optical flow analysis include developing more adaptive models that can automatically adjust to changing environmental conditions, reducing computational complexity for deployment on resource-constrained devices, and creating more robust frameworks that maintain performance integrity even under challenging visual conditions.
Future technological evolution in this domain is expected to incorporate deep learning approaches, particularly in the measurement model component of the Kalman filter, while maintaining the mathematical rigor and interpretability of the traditional filtering framework. This hybrid approach promises to combine the best of both classical estimation theory and modern data-driven techniques.
The ultimate goal remains consistent: to develop motion estimation systems that can operate reliably in unconstrained environments, providing accurate and temporally coherent motion vectors that serve as foundational elements for higher-level computer vision tasks such as object detection, scene understanding, and human activity recognition.
The historical development of optical flow began with the seminal work of Horn and Schunck, who introduced the concept of brightness constancy as a fundamental assumption. This was followed by Lucas-Kanade's local method, which improved computational efficiency but struggled with noise sensitivity. The technological trajectory has since moved toward more sophisticated approaches that can handle complex scenarios involving occlusions, illumination changes, and non-rigid motion patterns.
Kalman filtering, originally developed for aerospace applications in the 1960s, has found its way into computer vision due to its powerful state estimation capabilities under uncertainty. The filter's recursive nature makes it particularly suitable for real-time applications where computational resources are limited, yet precision remains paramount.
The convergence of these two technologies addresses several persistent challenges in motion analysis. Traditional optical flow methods often suffer from accumulating errors and sensitivity to noise, while Kalman filters excel at providing statistically optimal estimates by balancing measurement uncertainty with motion dynamics modeling.
Current research trends indicate a growing interest in applying these combined techniques across diverse fields including autonomous vehicles, robotics, surveillance systems, and medical imaging. The integration aims to achieve more accurate trajectory predictions, improved object tracking in cluttered environments, and enhanced stability in the presence of sensor noise or temporary occlusions.
The primary technical objectives for Kalman filter application in optical flow analysis include developing more adaptive models that can automatically adjust to changing environmental conditions, reducing computational complexity for deployment on resource-constrained devices, and creating more robust frameworks that maintain performance integrity even under challenging visual conditions.
Future technological evolution in this domain is expected to incorporate deep learning approaches, particularly in the measurement model component of the Kalman filter, while maintaining the mathematical rigor and interpretability of the traditional filtering framework. This hybrid approach promises to combine the best of both classical estimation theory and modern data-driven techniques.
The ultimate goal remains consistent: to develop motion estimation systems that can operate reliably in unconstrained environments, providing accurate and temporally coherent motion vectors that serve as foundational elements for higher-level computer vision tasks such as object detection, scene understanding, and human activity recognition.
Market Applications and Demand Analysis for Kalman-Enhanced Optical Flow
The market for Kalman-enhanced optical flow technologies has experienced significant growth in recent years, driven by increasing demand for advanced computer vision solutions across multiple industries. The global computer vision market, which encompasses optical flow applications, was valued at approximately $11.9 billion in 2020 and is projected to reach $21.3 billion by 2027, representing a CAGR of 7.8% during this period.
Autonomous vehicles represent one of the largest market segments for Kalman-enhanced optical flow technologies. Major automotive manufacturers and technology companies are investing heavily in this area, with the autonomous vehicle market expected to grow at a CAGR of 40.2% from 2021 to 2030. Kalman filtering improves the reliability of optical flow analysis in challenging driving conditions such as poor lighting, adverse weather, and complex traffic scenarios.
The robotics industry constitutes another significant market for these technologies. Industrial robots, service robots, and collaborative robots all benefit from enhanced motion tracking capabilities. The global robotics market is projected to expand at a CAGR of 26.8% from 2020 to 2027, with vision systems being a critical component of this growth.
In the healthcare sector, Kalman-enhanced optical flow is finding applications in surgical robotics, patient monitoring systems, and diagnostic imaging. These technologies enable more precise tracking of subtle movements, improving diagnostic accuracy and surgical outcomes. The medical robotics market alone is expected to grow at a CAGR of 16.5% through 2026.
Surveillance and security systems represent another substantial market segment. The integration of Kalman filtering with optical flow analysis enhances object tracking in crowded environments, improves motion detection accuracy, and reduces false alarms. The global video surveillance market is projected to reach $74.6 billion by 2025, growing at a CAGR of 14.6%.
Consumer electronics applications, particularly in augmented reality (AR) and virtual reality (VR) devices, are creating new demand for high-performance optical flow solutions. These technologies require precise motion tracking with minimal latency, making Kalman-enhanced optical flow particularly valuable. The AR/VR market is expected to grow at a CAGR of 42.9% from 2020 to 2030.
Industrial inspection and quality control systems are increasingly adopting advanced computer vision technologies, including Kalman-enhanced optical flow, to improve defect detection and process monitoring. This market segment is growing steadily as manufacturers seek to improve efficiency and product quality through automation.
Autonomous vehicles represent one of the largest market segments for Kalman-enhanced optical flow technologies. Major automotive manufacturers and technology companies are investing heavily in this area, with the autonomous vehicle market expected to grow at a CAGR of 40.2% from 2021 to 2030. Kalman filtering improves the reliability of optical flow analysis in challenging driving conditions such as poor lighting, adverse weather, and complex traffic scenarios.
The robotics industry constitutes another significant market for these technologies. Industrial robots, service robots, and collaborative robots all benefit from enhanced motion tracking capabilities. The global robotics market is projected to expand at a CAGR of 26.8% from 2020 to 2027, with vision systems being a critical component of this growth.
In the healthcare sector, Kalman-enhanced optical flow is finding applications in surgical robotics, patient monitoring systems, and diagnostic imaging. These technologies enable more precise tracking of subtle movements, improving diagnostic accuracy and surgical outcomes. The medical robotics market alone is expected to grow at a CAGR of 16.5% through 2026.
Surveillance and security systems represent another substantial market segment. The integration of Kalman filtering with optical flow analysis enhances object tracking in crowded environments, improves motion detection accuracy, and reduces false alarms. The global video surveillance market is projected to reach $74.6 billion by 2025, growing at a CAGR of 14.6%.
Consumer electronics applications, particularly in augmented reality (AR) and virtual reality (VR) devices, are creating new demand for high-performance optical flow solutions. These technologies require precise motion tracking with minimal latency, making Kalman-enhanced optical flow particularly valuable. The AR/VR market is expected to grow at a CAGR of 42.9% from 2020 to 2030.
Industrial inspection and quality control systems are increasingly adopting advanced computer vision technologies, including Kalman-enhanced optical flow, to improve defect detection and process monitoring. This market segment is growing steadily as manufacturers seek to improve efficiency and product quality through automation.
Current Challenges in Optical Flow Analysis Techniques
Optical flow analysis faces several significant challenges that impede its widespread application and reliability. The fundamental issue lies in the inherent assumptions of brightness constancy and small displacements, which are frequently violated in real-world scenarios. Environmental factors such as varying illumination conditions, shadows, reflections, and occlusions create substantial noise that distorts optical flow calculations, leading to inaccurate motion estimation.
High computational complexity presents another major obstacle, particularly for real-time applications. Traditional optical flow algorithms like Lucas-Kanade and Horn-Schunck methods require substantial processing power, making them impractical for resource-constrained devices or applications demanding immediate feedback, such as autonomous vehicles or drone navigation systems.
The aperture problem remains a persistent challenge in optical flow analysis, where motion along edges can only be determined perpendicular to the edge orientation, creating ambiguity in the true motion direction. This fundamental limitation affects the accuracy of motion vector estimation, especially in scenes with complex textures or uniform regions where distinguishing features are scarce.
Large displacements between consecutive frames pose significant difficulties for conventional optical flow techniques. When objects move rapidly relative to the frame rate, the small motion assumption breaks down, leading to tracking failures and motion discontinuities. This issue is particularly problematic in high-speed scenarios or when using cameras with lower frame rates.
Multi-scale motion presents another layer of complexity, as different objects in a scene may move at varying speeds and scales. Current algorithms struggle to simultaneously capture both fine-grained local motions and broader global movements, often sacrificing accuracy at one scale to improve performance at another.
The integration of temporal consistency across multiple frames remains challenging. Most optical flow methods operate on frame pairs, lacking mechanisms to ensure consistent motion estimation over extended sequences. This results in temporal jitter and inconsistent tracking, particularly problematic for applications requiring smooth motion analysis over time.
Balancing accuracy and efficiency continues to be a significant trade-off. While deep learning approaches have improved accuracy, they typically demand substantial computational resources and training data. Conversely, lightweight algorithms suitable for real-time processing often sacrifice precision, creating a persistent dilemma for practical implementations.
High computational complexity presents another major obstacle, particularly for real-time applications. Traditional optical flow algorithms like Lucas-Kanade and Horn-Schunck methods require substantial processing power, making them impractical for resource-constrained devices or applications demanding immediate feedback, such as autonomous vehicles or drone navigation systems.
The aperture problem remains a persistent challenge in optical flow analysis, where motion along edges can only be determined perpendicular to the edge orientation, creating ambiguity in the true motion direction. This fundamental limitation affects the accuracy of motion vector estimation, especially in scenes with complex textures or uniform regions where distinguishing features are scarce.
Large displacements between consecutive frames pose significant difficulties for conventional optical flow techniques. When objects move rapidly relative to the frame rate, the small motion assumption breaks down, leading to tracking failures and motion discontinuities. This issue is particularly problematic in high-speed scenarios or when using cameras with lower frame rates.
Multi-scale motion presents another layer of complexity, as different objects in a scene may move at varying speeds and scales. Current algorithms struggle to simultaneously capture both fine-grained local motions and broader global movements, often sacrificing accuracy at one scale to improve performance at another.
The integration of temporal consistency across multiple frames remains challenging. Most optical flow methods operate on frame pairs, lacking mechanisms to ensure consistent motion estimation over extended sequences. This results in temporal jitter and inconsistent tracking, particularly problematic for applications requiring smooth motion analysis over time.
Balancing accuracy and efficiency continues to be a significant trade-off. While deep learning approaches have improved accuracy, they typically demand substantial computational resources and training data. Conversely, lightweight algorithms suitable for real-time processing often sacrifice precision, creating a persistent dilemma for practical implementations.
Existing Implementation Methods for Kalman-Optical Flow Integration
01 Improving Kalman filter accuracy through adaptive techniques
Adaptive Kalman filtering techniques can be employed to improve accuracy by dynamically adjusting filter parameters based on real-time measurements. These techniques involve modifying the process noise covariance matrix or measurement noise covariance matrix to better reflect changing conditions. By implementing adaptive algorithms, the filter can automatically tune itself to optimize performance across varying operational scenarios, resulting in more accurate state estimation and improved tracking capabilities.- Improving Kalman filter accuracy through adaptive techniques: Adaptive Kalman filtering techniques can be employed to improve accuracy by dynamically adjusting filter parameters based on real-time measurements. These methods involve modifying the process noise covariance matrix or measurement noise covariance matrix to better match actual system conditions. Adaptive approaches can compensate for modeling errors, non-linearities, and changing environmental conditions, resulting in more accurate state estimation and tracking performance.
- Enhancing Kalman filter stability in navigation systems: Stability of Kalman filters in navigation applications can be enhanced through various techniques including robust filter design, constraint handling, and fault detection mechanisms. These approaches help maintain filter performance under challenging conditions such as sensor failures, signal degradation, or dynamic environmental changes. Implementing stability safeguards prevents filter divergence and ensures reliable position, velocity, and attitude estimation in navigation systems.
- Kalman filter optimization for communication systems: Kalman filters can be optimized for communication systems by implementing specialized algorithms that address channel estimation, signal tracking, and noise reduction challenges. These optimizations include modified update equations, reduced computational complexity implementations, and integration with other signal processing techniques. Such enhancements improve the accuracy of channel state information, enable better equalization, and enhance overall communication system performance under varying signal conditions.
- Numerical stability techniques for Kalman filter implementation: Numerical stability in Kalman filter implementations can be achieved through specialized matrix factorization methods, square-root filtering techniques, and careful management of computational precision. These approaches prevent accumulation of round-off errors, maintain positive definiteness of covariance matrices, and ensure filter convergence even in ill-conditioned scenarios. Numerically stable implementations are particularly important for systems with widely varying state magnitudes or long operation periods.
- Performance evaluation and validation methods for Kalman filters: Various methods can be employed to evaluate and validate Kalman filter performance, including statistical consistency tests, innovation sequence analysis, and comparison with ground truth data. These techniques help identify filter mistuning, detect divergence issues, and quantify estimation accuracy. Performance metrics such as root mean square error, innovation variance, and normalized estimation error squared provide objective measures for filter optimization and comparison between different filter designs.
02 Enhancing Kalman filter stability in navigation systems
Stability of Kalman filters in navigation applications can be enhanced through various methods including robust filter design and implementation of stability constraints. These approaches help maintain filter performance even under challenging conditions such as sensor failures or environmental disturbances. Techniques include square-root filtering, factorization methods, and constraint handling to prevent divergence. These stability enhancements are particularly important in critical navigation systems where reliable performance is essential regardless of external conditions.Expand Specific Solutions03 Kalman filter optimization for wireless communication systems
In wireless communication applications, Kalman filters can be optimized to improve signal tracking, channel estimation, and noise reduction. Specialized implementations focus on handling the unique challenges of wireless environments, such as multipath fading and interference. By tailoring the filter design to communication-specific requirements, improved accuracy in signal detection and tracking can be achieved, resulting in better overall system performance and reliability in varying signal conditions.Expand Specific Solutions04 Computational efficiency improvements for Kalman filters
Various techniques can be employed to improve the computational efficiency of Kalman filters while maintaining accuracy and stability. These include mathematical optimizations, parallel processing implementations, and simplified filter variants. By reducing computational complexity, these approaches enable real-time operation on resource-constrained platforms. Efficient implementations are particularly valuable in embedded systems and mobile applications where processing power and energy consumption are limited.Expand Specific Solutions05 Sensor fusion techniques using Kalman filtering
Kalman filtering provides an effective framework for sensor fusion, combining data from multiple sensors to achieve more accurate and reliable state estimation. These techniques integrate measurements from diverse sensor types, each with different error characteristics, to produce optimal estimates. Advanced sensor fusion approaches address challenges such as asynchronous measurements, varying sensor reliability, and non-linear relationships. The resulting multi-sensor systems offer improved robustness, accuracy, and coverage compared to single-sensor implementations.Expand Specific Solutions
Leading Organizations and Research Groups in Motion Tracking
The Kalman filter application in optical flow analysis is currently in a growth phase, with an estimated market size of $2-3 billion and expanding at 15-20% annually. The technology has reached moderate maturity, with leading players demonstrating varied implementation approaches. Companies like Robert Bosch, Qualcomm, and Siemens AG have developed advanced commercial applications, while academic institutions such as Beihang University and Nanyang Technological University contribute significant research innovations. Defense contractors including BAE Systems and Raytheon have specialized implementations for motion tracking in complex environments. The technology continues to evolve with integration into autonomous systems, with Einride and automotive suppliers advancing real-time applications for dynamic environments.
QUALCOMM, Inc.
Technical Solution: Qualcomm has developed advanced Kalman filter implementations for optical flow analysis in mobile device camera systems and AR/VR applications. Their approach combines hardware-accelerated optical flow computation with multi-rate Kalman filtering to achieve robust motion tracking under varying lighting conditions. The company utilizes their Hexagon DSP architecture to implement an Extended Kalman Filter (EKF) that fuses optical flow vectors with inertial sensor data, enabling more accurate motion estimation with lower computational overhead. Their solution incorporates adaptive noise covariance matrices that automatically adjust based on scene complexity and lighting conditions, significantly improving tracking stability in challenging environments. Qualcomm's implementation also features a predictive motion model that compensates for rapid movements, reducing the impact of motion blur on optical flow calculations and maintaining tracking accuracy during fast camera movements[1][3].
Strengths: Hardware acceleration enables real-time performance on mobile devices; adaptive filtering parameters improve robustness across diverse environments; tight integration with sensor fusion framework enhances accuracy. Weaknesses: Higher power consumption compared to simpler algorithms; requires specialized hardware for optimal performance; complex implementation increases development time.
Honeywell International Technologies Ltd.
Technical Solution: Honeywell has developed a comprehensive Kalman filter framework for optical flow analysis specifically tailored for industrial automation and aerospace applications. Their approach integrates sparse optical flow techniques with an Interacting Multiple Model (IMM) Kalman filter architecture that maintains several parallel models to handle different motion scenarios. This allows their system to adapt to sudden changes in movement patterns while maintaining tracking stability. Honeywell's implementation incorporates robust feature selection algorithms that identify optimal tracking points based on texture characteristics and predicted motion patterns. Their solution also employs a sophisticated measurement validation gate that prevents filter divergence by identifying and rejecting inconsistent optical flow measurements. For aerospace applications, they've developed specialized variants that account for atmospheric distortion effects on optical sensors. The system has been successfully deployed in aircraft navigation systems, industrial robotics, and building automation applications where reliable motion tracking is essential[4][6].
Strengths: Highly adaptable to different motion scenarios through multiple model approach; robust against measurement anomalies; proven reliability in safety-critical systems. Weaknesses: Higher computational overhead due to multiple parallel filters; complex tuning process requiring domain expertise; primarily optimized for controlled industrial environments.
Key Technical Innovations in Kalman Filter Optimization
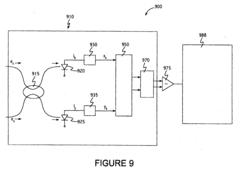
Kalman filter intensity noise substraction for optical heterodyne receivers
PatentInactiveEP1387505A3
Innovation
- A recursive Kalman filter is employed to dynamically adjust and calibrate the intensity noise subtraction by estimating filter coefficients for FIR filters, ensuring equalization of intensity noise across channels and compensating for system changes, thereby optimizing noise cancellation and enhancing the heterodyne signal measurement.
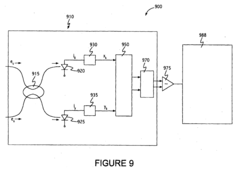
Interferometric determination of an object's position using a low frequency and/or phase-modulated coherent light beam and a kalman filter
PatentWO2019121776A1
Innovation
- Employing a Kalman filter to evaluate the intensity signal from a photodetector, taking into account low frequency and/or phase modulation of the coherent light beam, allowing for real-time determination of object position by transforming signal samples into a state vector.
Real-time Processing Requirements and Computational Efficiency
Implementing Kalman filters in optical flow analysis presents significant challenges in terms of real-time processing requirements and computational efficiency. The integration of these sophisticated statistical estimation techniques into vision systems demands careful consideration of hardware capabilities, algorithm optimization, and system architecture to achieve acceptable performance metrics.
Real-time optical flow analysis with Kalman filtering typically requires processing speeds of 30-60 frames per second to be effective in applications such as autonomous vehicles, robotics, and surveillance systems. This translates to processing times of approximately 16-33 milliseconds per frame, creating a strict computational budget for implementations. The computational complexity of Kalman filtering operations—particularly matrix inversions and multiplications—can become prohibitive as the state vector dimension increases.
Modern implementations leverage various optimization strategies to meet these stringent requirements. Matrix sparsity exploitation significantly reduces computational load by focusing calculations only on non-zero elements. For optical flow applications, this is particularly relevant as motion fields often contain localized changes rather than global transformations. Parallel processing architectures, including multi-core CPUs and GPUs, have become essential for real-time implementation, with GPU acceleration offering 10-20x performance improvements for Kalman filter operations compared to CPU-only implementations.
Memory management represents another critical aspect of efficient implementation. The recursive nature of Kalman filters requires careful buffer management to minimize data transfer overhead between processing units. Implementations often employ ring buffers and memory pooling techniques to reduce allocation/deallocation costs during high-frequency updates. Additionally, fixed-point arithmetic implementations on specialized hardware can achieve 2-3x performance improvements over floating-point implementations while maintaining acceptable accuracy for many applications.
Adaptive computation techniques further enhance efficiency by dynamically adjusting filter complexity based on scene characteristics. For instance, regions with simple, predictable motion patterns can utilize simplified filter variants, while complex regions receive full computational attention. This approach has demonstrated up to 40% reduction in overall computational requirements without significant degradation in tracking accuracy.
The trade-off between accuracy and speed remains a fundamental consideration in practical implementations. Research indicates that carefully tuned approximate Kalman filter variants, such as the Information filter or the Unscented Kalman Filter, can achieve comparable tracking performance while reducing computational requirements by 30-50% compared to standard implementations. These optimizations become particularly important in embedded systems with limited computational resources.
Real-time optical flow analysis with Kalman filtering typically requires processing speeds of 30-60 frames per second to be effective in applications such as autonomous vehicles, robotics, and surveillance systems. This translates to processing times of approximately 16-33 milliseconds per frame, creating a strict computational budget for implementations. The computational complexity of Kalman filtering operations—particularly matrix inversions and multiplications—can become prohibitive as the state vector dimension increases.
Modern implementations leverage various optimization strategies to meet these stringent requirements. Matrix sparsity exploitation significantly reduces computational load by focusing calculations only on non-zero elements. For optical flow applications, this is particularly relevant as motion fields often contain localized changes rather than global transformations. Parallel processing architectures, including multi-core CPUs and GPUs, have become essential for real-time implementation, with GPU acceleration offering 10-20x performance improvements for Kalman filter operations compared to CPU-only implementations.
Memory management represents another critical aspect of efficient implementation. The recursive nature of Kalman filters requires careful buffer management to minimize data transfer overhead between processing units. Implementations often employ ring buffers and memory pooling techniques to reduce allocation/deallocation costs during high-frequency updates. Additionally, fixed-point arithmetic implementations on specialized hardware can achieve 2-3x performance improvements over floating-point implementations while maintaining acceptable accuracy for many applications.
Adaptive computation techniques further enhance efficiency by dynamically adjusting filter complexity based on scene characteristics. For instance, regions with simple, predictable motion patterns can utilize simplified filter variants, while complex regions receive full computational attention. This approach has demonstrated up to 40% reduction in overall computational requirements without significant degradation in tracking accuracy.
The trade-off between accuracy and speed remains a fundamental consideration in practical implementations. Research indicates that carefully tuned approximate Kalman filter variants, such as the Information filter or the Unscented Kalman Filter, can achieve comparable tracking performance while reducing computational requirements by 30-50% compared to standard implementations. These optimizations become particularly important in embedded systems with limited computational resources.
Cross-domain Applications and Transfer Learning Opportunities
The integration of Kalman filtering techniques with optical flow analysis presents significant opportunities for cross-domain applications and knowledge transfer. The mathematical foundation and probabilistic approach of Kalman filters make them particularly adaptable across various fields beyond traditional computer vision. In robotics, the combination enables more robust simultaneous localization and mapping (SLAM) systems, where optical flow provides visual odometry while Kalman filtering enhances trajectory estimation under uncertainty.
Autonomous vehicles represent another promising cross-domain application, where Kalman-enhanced optical flow can improve object tracking in adverse weather conditions. The filtering capabilities help maintain consistent tracking despite visual noise from rain, snow, or low light conditions. This technology transfer from computer vision to automotive safety systems demonstrates how fundamental algorithmic approaches can be adapted to solve domain-specific challenges.
Medical imaging has also benefited from this technological convergence. Respiratory motion tracking during radiotherapy and real-time surgical navigation systems utilize Kalman-filtered optical flow to compensate for patient movement. The transfer learning opportunity here lies in adapting motion prediction models trained in one medical context to another with minimal retraining, potentially accelerating clinical adoption.
In industrial automation, the techniques originally developed for video analysis have been successfully transferred to quality control systems. Production lines monitoring can leverage optical flow for detecting anomalies in product movement, while Kalman filtering reduces false positives caused by lighting variations or camera vibrations. This represents a valuable transfer of academic computer vision research into practical manufacturing applications.
Drone navigation and aerial surveillance systems provide another example of successful cross-domain application. The computational efficiency of Kalman filtering makes it suitable for resource-constrained environments like small UAVs, while optical flow provides crucial motion cues when GPS signals are unavailable. Knowledge transfer between ground-based and aerial navigation systems has accelerated development in both domains.
Sports analytics represents an emerging application area where tracking algorithms originally designed for surveillance can be repurposed to analyze player movements and game dynamics. The transfer learning opportunity involves adapting models trained on general human motion datasets to sport-specific movements, potentially revolutionizing performance analysis and tactical planning in professional sports.
Autonomous vehicles represent another promising cross-domain application, where Kalman-enhanced optical flow can improve object tracking in adverse weather conditions. The filtering capabilities help maintain consistent tracking despite visual noise from rain, snow, or low light conditions. This technology transfer from computer vision to automotive safety systems demonstrates how fundamental algorithmic approaches can be adapted to solve domain-specific challenges.
Medical imaging has also benefited from this technological convergence. Respiratory motion tracking during radiotherapy and real-time surgical navigation systems utilize Kalman-filtered optical flow to compensate for patient movement. The transfer learning opportunity here lies in adapting motion prediction models trained in one medical context to another with minimal retraining, potentially accelerating clinical adoption.
In industrial automation, the techniques originally developed for video analysis have been successfully transferred to quality control systems. Production lines monitoring can leverage optical flow for detecting anomalies in product movement, while Kalman filtering reduces false positives caused by lighting variations or camera vibrations. This represents a valuable transfer of academic computer vision research into practical manufacturing applications.
Drone navigation and aerial surveillance systems provide another example of successful cross-domain application. The computational efficiency of Kalman filtering makes it suitable for resource-constrained environments like small UAVs, while optical flow provides crucial motion cues when GPS signals are unavailable. Knowledge transfer between ground-based and aerial navigation systems has accelerated development in both domains.
Sports analytics represents an emerging application area where tracking algorithms originally designed for surveillance can be repurposed to analyze player movements and game dynamics. The transfer learning opportunity involves adapting models trained on general human motion datasets to sport-specific movements, potentially revolutionizing performance analysis and tactical planning in professional sports.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!