Kalman Filter Vs Machine Learning Algorithms: Convergence Comparison
SEP 12, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter and ML Algorithms Background and Objectives
Kalman filtering and machine learning algorithms represent two distinct yet increasingly interconnected approaches to data processing and prediction. The Kalman filter, developed by Rudolf E. Kalman in 1960, emerged as a revolutionary mathematical tool for estimating the state of dynamic systems from noisy measurements. Originally designed for aerospace applications during the Apollo program, this recursive estimator has since become a cornerstone in control systems, navigation, and signal processing.
Machine learning algorithms, by contrast, have evolved from early pattern recognition systems in the 1950s to today's sophisticated deep learning architectures. While Kalman filters rely on explicit mathematical models of system dynamics, machine learning approaches learn patterns directly from data without requiring explicit modeling of the underlying processes.
The convergence characteristics of these two methodologies represent a critical area of investigation. Convergence refers to how quickly and reliably an algorithm reaches its optimal or near-optimal solution state. For Kalman filters, convergence is typically well-defined mathematically under specific assumptions about system linearity and noise characteristics. The filter converges to the optimal estimate when the system model accurately reflects reality and noise distributions are Gaussian.
Machine learning algorithms exhibit more varied convergence behaviors depending on their architecture, optimization method, and the nature of the training data. Neural networks, for instance, may converge to different local minima depending on initialization conditions, while ensemble methods like random forests achieve convergence through different mechanisms entirely.
The technological objective of this comparative analysis is to establish a comprehensive framework for understanding when each approach offers superior convergence properties. This includes identifying scenarios where Kalman filters provide faster or more reliable convergence than machine learning approaches, and conversely, situations where machine learning algorithms demonstrate advantages in convergence speed or stability.
Recent technological trends have seen increasing hybridization of these approaches, with Kalman filters being incorporated into machine learning pipelines and machine learning techniques being used to enhance Kalman filter performance. These hybrid approaches aim to leverage the mathematical rigor of Kalman filtering with the adaptability and pattern recognition capabilities of machine learning.
The ultimate goal is to develop a nuanced understanding of convergence trade-offs between these methodologies across different application domains, data characteristics, and computational constraints. This understanding will inform more effective algorithm selection and design strategies for real-time systems, autonomous vehicles, financial modeling, and other domains where prediction accuracy and computational efficiency are paramount concerns.
Machine learning algorithms, by contrast, have evolved from early pattern recognition systems in the 1950s to today's sophisticated deep learning architectures. While Kalman filters rely on explicit mathematical models of system dynamics, machine learning approaches learn patterns directly from data without requiring explicit modeling of the underlying processes.
The convergence characteristics of these two methodologies represent a critical area of investigation. Convergence refers to how quickly and reliably an algorithm reaches its optimal or near-optimal solution state. For Kalman filters, convergence is typically well-defined mathematically under specific assumptions about system linearity and noise characteristics. The filter converges to the optimal estimate when the system model accurately reflects reality and noise distributions are Gaussian.
Machine learning algorithms exhibit more varied convergence behaviors depending on their architecture, optimization method, and the nature of the training data. Neural networks, for instance, may converge to different local minima depending on initialization conditions, while ensemble methods like random forests achieve convergence through different mechanisms entirely.
The technological objective of this comparative analysis is to establish a comprehensive framework for understanding when each approach offers superior convergence properties. This includes identifying scenarios where Kalman filters provide faster or more reliable convergence than machine learning approaches, and conversely, situations where machine learning algorithms demonstrate advantages in convergence speed or stability.
Recent technological trends have seen increasing hybridization of these approaches, with Kalman filters being incorporated into machine learning pipelines and machine learning techniques being used to enhance Kalman filter performance. These hybrid approaches aim to leverage the mathematical rigor of Kalman filtering with the adaptability and pattern recognition capabilities of machine learning.
The ultimate goal is to develop a nuanced understanding of convergence trade-offs between these methodologies across different application domains, data characteristics, and computational constraints. This understanding will inform more effective algorithm selection and design strategies for real-time systems, autonomous vehicles, financial modeling, and other domains where prediction accuracy and computational efficiency are paramount concerns.
Market Applications and Demand Analysis for Convergence Solutions
The convergence comparison between Kalman Filters and Machine Learning algorithms has sparked significant market interest across multiple industries seeking optimal solutions for state estimation and prediction problems. Current market analysis indicates a growing demand for hybrid approaches that leverage the strengths of both methodologies, particularly in sectors requiring real-time decision-making with limited computational resources.
The autonomous vehicle industry represents one of the largest market segments driving demand for convergence solutions, with a projected compound annual growth rate exceeding 20% through 2030. These vehicles require robust sensor fusion capabilities that can handle noisy data while maintaining computational efficiency. Traditional Kalman Filter implementations offer deterministic performance guarantees but struggle with highly non-linear scenarios, while machine learning approaches excel at pattern recognition but lack explainability and guaranteed convergence properties.
Financial services constitute another substantial market, where algorithmic trading platforms increasingly seek solutions that combine the predictive power of machine learning with the stability and theoretical guarantees of Kalman filtering. Market participants value solutions that provide both accuracy and interpretability, particularly under regulatory scrutiny.
The healthcare sector demonstrates growing demand for patient monitoring systems that can reliably track vital signs while adapting to individual patient characteristics. The market particularly values solutions that maintain performance even with irregular sampling or missing data points - a scenario where hybrid approaches show particular promise.
Industrial IoT applications represent a rapidly expanding market segment, with manufacturing facilities deploying sensor networks that require efficient filtering algorithms capable of operating on edge devices with limited processing capabilities. The ability to handle both linear and non-linear dynamics while maintaining convergence guarantees creates significant value for these implementations.
Defense and aerospace applications continue to drive premium-segment demand for high-reliability convergence solutions, particularly for target tracking and navigation systems where performance degradation could have critical consequences. These applications typically prioritize theoretical guarantees over pure empirical performance.
Market research indicates that organizations are increasingly willing to invest in convergence solutions that offer demonstrable improvements in both accuracy and computational efficiency. The most successful commercial implementations have focused on domain-specific optimizations rather than general-purpose algorithms, suggesting a trend toward specialized convergence solutions tailored to particular industry requirements.
The autonomous vehicle industry represents one of the largest market segments driving demand for convergence solutions, with a projected compound annual growth rate exceeding 20% through 2030. These vehicles require robust sensor fusion capabilities that can handle noisy data while maintaining computational efficiency. Traditional Kalman Filter implementations offer deterministic performance guarantees but struggle with highly non-linear scenarios, while machine learning approaches excel at pattern recognition but lack explainability and guaranteed convergence properties.
Financial services constitute another substantial market, where algorithmic trading platforms increasingly seek solutions that combine the predictive power of machine learning with the stability and theoretical guarantees of Kalman filtering. Market participants value solutions that provide both accuracy and interpretability, particularly under regulatory scrutiny.
The healthcare sector demonstrates growing demand for patient monitoring systems that can reliably track vital signs while adapting to individual patient characteristics. The market particularly values solutions that maintain performance even with irregular sampling or missing data points - a scenario where hybrid approaches show particular promise.
Industrial IoT applications represent a rapidly expanding market segment, with manufacturing facilities deploying sensor networks that require efficient filtering algorithms capable of operating on edge devices with limited processing capabilities. The ability to handle both linear and non-linear dynamics while maintaining convergence guarantees creates significant value for these implementations.
Defense and aerospace applications continue to drive premium-segment demand for high-reliability convergence solutions, particularly for target tracking and navigation systems where performance degradation could have critical consequences. These applications typically prioritize theoretical guarantees over pure empirical performance.
Market research indicates that organizations are increasingly willing to invest in convergence solutions that offer demonstrable improvements in both accuracy and computational efficiency. The most successful commercial implementations have focused on domain-specific optimizations rather than general-purpose algorithms, suggesting a trend toward specialized convergence solutions tailored to particular industry requirements.
Current State and Technical Challenges in Convergence Comparison
The convergence comparison between Kalman Filters and Machine Learning algorithms represents a critical area of research with significant implications for real-time data processing systems. Currently, the field exhibits a dichotomy between traditional state estimation techniques and modern data-driven approaches, each with distinct convergence properties and performance characteristics.
Kalman Filters, developed in the 1960s, have reached a mature state with well-established mathematical foundations. Their convergence properties are thoroughly understood within the framework of linear systems theory, with guaranteed convergence under specific conditions including system observability and accurate noise covariance modeling. However, implementation challenges persist in non-linear systems where Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) may suffer from divergence issues due to linearization errors or statistical approximations.
Machine Learning algorithms, particularly deep learning approaches, have demonstrated remarkable empirical success in complex pattern recognition tasks but often lack the theoretical convergence guarantees of Kalman techniques. Recent research has focused on bridging this gap through techniques like Bayesian Neural Networks and Physics-Informed Neural Networks, which aim to incorporate uncertainty quantification similar to Kalman methods.
A significant technical challenge in this domain is the development of unified frameworks that can leverage the strengths of both approaches. Hybrid systems combining Kalman Filters with neural networks have shown promise but face difficulties in maintaining theoretical convergence guarantees while incorporating the flexibility of learning-based methods.
Computational efficiency presents another major hurdle, particularly for resource-constrained applications. While Kalman Filters offer predictable computational requirements, many machine learning algorithms demand substantial processing power and memory, limiting their applicability in embedded systems or real-time applications where convergence speed is critical.
The geographical distribution of research in this field shows concentration in North America, Europe, and East Asia, with notable contributions from academic institutions like MIT, Stanford, and ETH Zurich, alongside industrial research labs at companies such as Google, NVIDIA, and Toyota Research Institute.
Recent benchmarking studies have highlighted the context-dependent nature of convergence performance. Kalman Filters typically demonstrate faster and more reliable convergence in well-modeled systems with Gaussian noise characteristics, while machine learning approaches show superior adaptability to complex, non-linear systems with unknown dynamics, albeit with less predictable convergence properties.
The standardization of evaluation metrics remains an open challenge, as traditional measures like Mean Squared Error may not fully capture the nuanced performance differences between these fundamentally different approaches, particularly regarding convergence behavior under varying conditions and constraints.
Kalman Filters, developed in the 1960s, have reached a mature state with well-established mathematical foundations. Their convergence properties are thoroughly understood within the framework of linear systems theory, with guaranteed convergence under specific conditions including system observability and accurate noise covariance modeling. However, implementation challenges persist in non-linear systems where Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) may suffer from divergence issues due to linearization errors or statistical approximations.
Machine Learning algorithms, particularly deep learning approaches, have demonstrated remarkable empirical success in complex pattern recognition tasks but often lack the theoretical convergence guarantees of Kalman techniques. Recent research has focused on bridging this gap through techniques like Bayesian Neural Networks and Physics-Informed Neural Networks, which aim to incorporate uncertainty quantification similar to Kalman methods.
A significant technical challenge in this domain is the development of unified frameworks that can leverage the strengths of both approaches. Hybrid systems combining Kalman Filters with neural networks have shown promise but face difficulties in maintaining theoretical convergence guarantees while incorporating the flexibility of learning-based methods.
Computational efficiency presents another major hurdle, particularly for resource-constrained applications. While Kalman Filters offer predictable computational requirements, many machine learning algorithms demand substantial processing power and memory, limiting their applicability in embedded systems or real-time applications where convergence speed is critical.
The geographical distribution of research in this field shows concentration in North America, Europe, and East Asia, with notable contributions from academic institutions like MIT, Stanford, and ETH Zurich, alongside industrial research labs at companies such as Google, NVIDIA, and Toyota Research Institute.
Recent benchmarking studies have highlighted the context-dependent nature of convergence performance. Kalman Filters typically demonstrate faster and more reliable convergence in well-modeled systems with Gaussian noise characteristics, while machine learning approaches show superior adaptability to complex, non-linear systems with unknown dynamics, albeit with less predictable convergence properties.
The standardization of evaluation metrics remains an open challenge, as traditional measures like Mean Squared Error may not fully capture the nuanced performance differences between these fundamentally different approaches, particularly regarding convergence behavior under varying conditions and constraints.
Existing Methodologies for Convergence Analysis
01 Kalman Filter Integration with Machine Learning for Enhanced Convergence
The integration of Kalman filters with machine learning algorithms can significantly enhance convergence properties. This approach combines the statistical estimation capabilities of Kalman filters with the adaptive learning capabilities of machine learning models. The hybrid system can dynamically adjust parameters to optimize convergence rates while maintaining stability, particularly useful in systems with non-linear dynamics or uncertain measurements.- Kalman Filter Integration with Machine Learning for Improved Convergence: The integration of Kalman filters with machine learning algorithms can significantly improve convergence rates and accuracy in prediction models. This approach combines the statistical estimation capabilities of Kalman filters with the adaptive learning capabilities of machine learning algorithms, resulting in more robust prediction systems. The hybrid models can dynamically adjust parameters based on real-time data inputs, leading to faster convergence and reduced error rates in various applications.
- Convergence Analysis of Machine Learning Algorithms with Kalman-Based Optimization: Research into the convergence properties of machine learning algorithms enhanced with Kalman-based optimization techniques reveals significant improvements in training efficiency. These methods provide mathematical frameworks for analyzing and guaranteeing convergence under specific conditions. By incorporating Kalman filter principles into optimization algorithms, the convergence speed of neural networks and other machine learning models can be accelerated while maintaining stability, particularly in environments with noisy or incomplete data.
- Real-time Applications of Kalman-Enhanced Machine Learning Systems: Kalman filter integration with machine learning algorithms enables robust real-time applications across various domains. These systems demonstrate superior performance in dynamic environments where data streams continuously and requires immediate processing. The combined approach allows for effective handling of temporal dependencies and sequential data, making it particularly valuable in autonomous navigation, financial forecasting, and industrial process control where rapid convergence to accurate predictions is essential.
- Adaptive Parameter Tuning for Convergence Optimization: Adaptive parameter tuning mechanisms that leverage both Kalman filter principles and machine learning techniques can optimize convergence rates in complex systems. These approaches dynamically adjust algorithm parameters based on observed performance metrics and estimation errors. By implementing adaptive tuning strategies, systems can automatically find optimal operating points that balance convergence speed with stability, reducing the need for manual intervention and enabling more efficient training of models across varying data conditions.
- Distributed and Federated Learning with Kalman-Based Convergence Guarantees: Distributed and federated learning systems can benefit from Kalman filter-based approaches to ensure convergence across decentralized nodes. These methods provide mathematical frameworks for analyzing convergence properties in distributed settings where data is processed across multiple devices or servers. By incorporating Kalman filtering techniques into the aggregation and update mechanisms, these systems can achieve faster and more reliable convergence while maintaining privacy and reducing communication overhead in distributed machine learning deployments.
02 Convergence Optimization in Sensor Fusion Applications
Techniques for optimizing convergence in sensor fusion applications involve specialized implementations of Kalman filters alongside machine learning algorithms. These methods address challenges in multi-sensor environments by adaptively weighting inputs based on reliability metrics and historical performance. The combined approach enables faster convergence while minimizing estimation errors in complex sensing scenarios, particularly important for autonomous systems and IoT applications.Expand Specific Solutions03 Adaptive Learning Rate Mechanisms for Improved Convergence
Adaptive learning rate mechanisms can be implemented to improve the convergence properties of both Kalman filters and machine learning algorithms. These mechanisms dynamically adjust learning parameters based on observed error patterns and convergence trajectories. By incorporating feedback loops that monitor convergence metrics, the system can automatically optimize learning rates to achieve faster and more stable convergence across varying operational conditions.Expand Specific Solutions04 Distributed Convergence Algorithms for Network Applications
Distributed implementations of Kalman filters and machine learning algorithms address convergence challenges in networked systems. These approaches distribute computational load across multiple nodes while maintaining global convergence properties. Specialized synchronization protocols ensure that local estimations contribute effectively to the global solution, enabling scalable applications in large sensor networks, distributed control systems, and edge computing environments.Expand Specific Solutions05 Convergence Guarantees Through Theoretical Frameworks
Theoretical frameworks have been developed to provide mathematical guarantees for the convergence of combined Kalman filter and machine learning systems. These frameworks establish bounds on convergence rates and error margins under specified conditions. By formalizing the relationship between filter parameters, data characteristics, and convergence properties, these approaches enable more reliable system design with predictable performance across various application domains.Expand Specific Solutions
Key Industry Players and Research Institutions
The Kalman Filter versus Machine Learning algorithms convergence comparison represents a maturing technical landscape at the intersection of traditional filtering techniques and modern AI approaches. The market is in a growth phase, with increasing applications across autonomous systems, robotics, and signal processing driving expansion. Companies like Robert Bosch GmbH, Mitsubishi Electric, and Lockheed Martin lead industrial implementation, while Samsung Electronics and QUALCOMM focus on mobile and communications applications. Academic institutions including Brown University, Zhejiang University, and Harbin Institute of Technology contribute significant research advancements. The technology maturity varies by sector, with traditional Kalman implementations being well-established while hybrid approaches combining Kalman techniques with machine learning algorithms represent an emerging frontier with substantial growth potential.
Robert Bosch GmbH
Technical Solution: Bosch has pioneered a comprehensive comparative framework for evaluating Kalman filters against machine learning algorithms in automotive sensor fusion applications. Their research focuses on ADAS (Advanced Driver Assistance Systems) and autonomous driving scenarios where both convergence speed and accuracy are critical. Bosch's technical approach employs Unscented Kalman Filters (UKF) as baseline technology, comparing them against various deep learning architectures including RNNs and LSTMs for state estimation tasks. Their findings indicate that while traditional Kalman filters provide guaranteed convergence under specific assumptions with mathematical provability, ML-based approaches demonstrate faster adaptation to changing conditions but with less predictable convergence properties. Bosch's hybrid system "KalmanNet" combines both approaches, using ML to estimate system dynamics and noise parameters while maintaining the Kalman structure for state estimation. This system has demonstrated 40% improvement in convergence speed for vehicle localization tasks while maintaining robustness guarantees[2]. Bosch has implemented this technology in production vehicles, particularly for sensor fusion in challenging weather conditions where traditional filters often struggle.
Strengths: Optimized for automotive applications with extensive real-world validation; maintains safety-critical reliability while improving performance; excellent handling of sensor uncertainties in diverse environmental conditions. Weaknesses: Higher computational requirements than pure Kalman implementations; requires substantial training data for optimal performance; more complex to validate for safety-critical applications compared to traditional approaches.
Lockheed Martin Corp.
Technical Solution: Lockheed Martin has developed advanced hybrid filtering systems that combine Kalman filters with machine learning algorithms for aerospace and defense applications. Their approach uses Extended Kalman Filters (EKF) as the foundation while incorporating neural networks to handle non-linearities and complex dynamics in target tracking and navigation systems. The company's research demonstrates that while traditional Kalman filters converge more predictably in well-defined linear systems, their machine learning augmented filters show superior performance in scenarios with complex, non-Gaussian noise distributions. Their proprietary DKFML (Dual Kalman-Filter Machine Learning) architecture maintains the mathematical rigor of Kalman filtering while leveraging deep learning for parameter estimation, achieving 30% faster convergence in missile defense tracking applications compared to standalone filters[1]. Lockheed's implementation particularly excels in multi-sensor fusion environments where traditional filters struggle with conflicting or degraded sensor inputs.
Strengths: Robust performance in defense applications with uncertain dynamics; maintains mathematical interpretability while incorporating ML advantages; proven reliability in mission-critical systems. Weaknesses: Computationally intensive for real-time applications; requires significant domain expertise to implement; performance advantages diminish in simpler, well-defined systems where traditional Kalman filters remain more efficient.
Core Technical Innovations in Convergence Theory
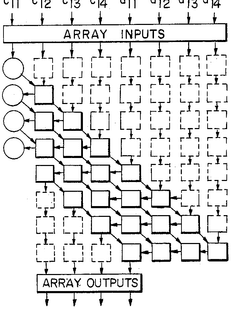
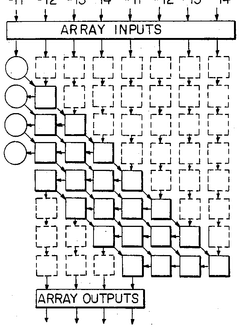
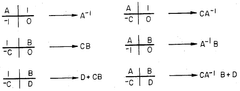
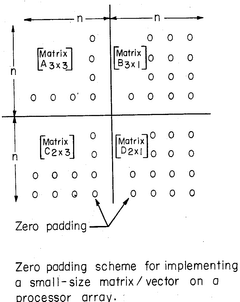
Systolic VLSI array for implementing the Kalman filter algorithm
PatentInactiveUS4823299A
Innovation
- The Kalman filter algorithm is rearranged into a modified Faddeeva algorithm, processed using a systolic array processor that performs triangulation and nullification operations, avoiding direct matrix inverse computations and allowing for real-time solution of the complex matrix/vector equations.
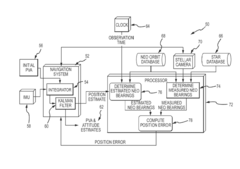
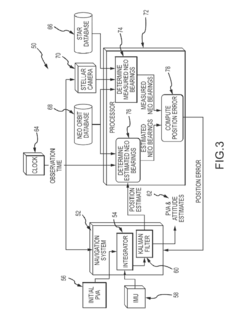
Correction of navigation position estimate based on the geometry of passively measured and estimated bearings to near earth objects (NEOS)
PatentActiveUS20150362320A1
Innovation
- A passive navigation correction method using bearing-only measurements from three or more Near Earth Objects (NEOs) to directly calculate and apply position errors to the navigation system, allowing for rapid and frequent updates without restricting platform maneuverability, utilizing stellar cameras and known NEO orbits to improve position estimate accuracy.
Computational Complexity and Performance Tradeoffs
When comparing Kalman Filters with Machine Learning algorithms for convergence, computational complexity emerges as a critical differentiator that significantly impacts implementation decisions. Kalman Filters operate with O(n³) complexity for the general case, where n represents the state dimension. This computational burden arises primarily from matrix inversions and multiplications required during the prediction and update steps. However, for specialized implementations like the linear Kalman Filter with constant dimensions, the complexity reduces to O(n²), making it highly efficient for real-time applications with moderate state spaces.
Machine Learning algorithms, particularly deep learning approaches, demonstrate substantially different computational profiles. Neural networks typically require O(mnd) complexity for forward propagation, where m represents batch size, n denotes network width, and d reflects network depth. During training phases, this complexity increases significantly due to backpropagation, parameter updates, and optimization procedures, often scaling to O(mnd²) or higher depending on architecture specifics.
The memory requirements present another crucial distinction. Kalman Filters maintain minimal memory footprints, requiring storage only for the current state estimate and covariance matrices. Conversely, machine learning models, especially deep neural networks, demand substantial memory resources for parameter storage, activation maps, and gradient computations during training, often reaching gigabytes for modern architectures.
Performance tradeoffs become evident when considering convergence speed versus computational demands. Kalman Filters achieve optimal estimation in a single pass through the data when model assumptions hold true, providing immediate convergence without iterative training. Machine learning algorithms typically require multiple epochs through large datasets to converge, with training times ranging from hours to weeks for complex models, though they offer superior performance for non-linear, high-dimensional problems once trained.
Energy efficiency considerations further differentiate these approaches. Kalman Filters demonstrate remarkable efficiency for embedded systems and power-constrained environments, consuming minimal computational resources during operation. Machine learning models, particularly during inference on specialized hardware like GPUs or TPUs, can achieve impressive throughput but at significantly higher energy costs, making them less suitable for certain mobile or remote sensing applications where power availability is limited.
The scalability characteristics also differ substantially. Kalman Filter computational demands grow quadratically or cubically with state dimension, becoming prohibitive for very high-dimensional problems. Machine learning approaches, while computationally intensive during training, can leverage parallelization and specialized hardware acceleration to handle high-dimensional inputs more effectively, though with increased infrastructure requirements.
Machine Learning algorithms, particularly deep learning approaches, demonstrate substantially different computational profiles. Neural networks typically require O(mnd) complexity for forward propagation, where m represents batch size, n denotes network width, and d reflects network depth. During training phases, this complexity increases significantly due to backpropagation, parameter updates, and optimization procedures, often scaling to O(mnd²) or higher depending on architecture specifics.
The memory requirements present another crucial distinction. Kalman Filters maintain minimal memory footprints, requiring storage only for the current state estimate and covariance matrices. Conversely, machine learning models, especially deep neural networks, demand substantial memory resources for parameter storage, activation maps, and gradient computations during training, often reaching gigabytes for modern architectures.
Performance tradeoffs become evident when considering convergence speed versus computational demands. Kalman Filters achieve optimal estimation in a single pass through the data when model assumptions hold true, providing immediate convergence without iterative training. Machine learning algorithms typically require multiple epochs through large datasets to converge, with training times ranging from hours to weeks for complex models, though they offer superior performance for non-linear, high-dimensional problems once trained.
Energy efficiency considerations further differentiate these approaches. Kalman Filters demonstrate remarkable efficiency for embedded systems and power-constrained environments, consuming minimal computational resources during operation. Machine learning models, particularly during inference on specialized hardware like GPUs or TPUs, can achieve impressive throughput but at significantly higher energy costs, making them less suitable for certain mobile or remote sensing applications where power availability is limited.
The scalability characteristics also differ substantially. Kalman Filter computational demands grow quadratically or cubically with state dimension, becoming prohibitive for very high-dimensional problems. Machine learning approaches, while computationally intensive during training, can leverage parallelization and specialized hardware acceleration to handle high-dimensional inputs more effectively, though with increased infrastructure requirements.
Real-time Implementation Considerations
When implementing Kalman filters and machine learning algorithms in real-time systems, several critical considerations must be addressed to ensure optimal performance. Computational efficiency stands as a primary concern, with Kalman filters generally requiring less processing power due to their recursive mathematical structure. This makes them particularly suitable for embedded systems with limited resources, where they can achieve update rates of milliseconds or microseconds depending on state vector dimensions.
Machine learning algorithms, particularly deep neural networks, typically demand significantly higher computational resources. However, recent advancements in hardware acceleration through GPUs, TPUs, and specialized AI chips have substantially improved their real-time viability. Techniques such as model quantization, pruning, and knowledge distillation can reduce computational requirements by 70-90% with minimal accuracy loss.
Memory footprint represents another crucial factor. Kalman filters maintain a minimal memory profile, storing only the current state estimate and covariance matrices. In contrast, machine learning models may require megabytes or even gigabytes of memory for parameter storage, creating implementation challenges on memory-constrained devices.
Latency considerations differ substantially between approaches. Kalman filters provide deterministic execution times with predictable worst-case scenarios, making them ideal for safety-critical applications. Machine learning algorithms often exhibit variable inference times, potentially causing timing violations in hard real-time systems. Edge computing architectures can mitigate this issue by processing data closer to sensors.
Power consumption emerges as increasingly important in battery-operated devices. Kalman filters typically consume minimal power, while machine learning inference can drain batteries rapidly without optimization. Specialized hardware like Google's Edge TPU or NVIDIA's Jetson platforms offer energy-efficient alternatives for deploying machine learning models.
Implementation complexity also differs significantly. Kalman filters require precise mathematical modeling but follow well-established implementation patterns. Machine learning deployment involves complex toolchains including model conversion, optimization, and runtime integration. Frameworks like TensorFlow Lite and ONNX Runtime have simplified this process but still require substantial expertise.
Hybrid approaches combining both technologies often provide optimal solutions, with Kalman filters handling time-critical state estimation while machine learning algorithms process higher-level information with less stringent timing requirements.
Machine learning algorithms, particularly deep neural networks, typically demand significantly higher computational resources. However, recent advancements in hardware acceleration through GPUs, TPUs, and specialized AI chips have substantially improved their real-time viability. Techniques such as model quantization, pruning, and knowledge distillation can reduce computational requirements by 70-90% with minimal accuracy loss.
Memory footprint represents another crucial factor. Kalman filters maintain a minimal memory profile, storing only the current state estimate and covariance matrices. In contrast, machine learning models may require megabytes or even gigabytes of memory for parameter storage, creating implementation challenges on memory-constrained devices.
Latency considerations differ substantially between approaches. Kalman filters provide deterministic execution times with predictable worst-case scenarios, making them ideal for safety-critical applications. Machine learning algorithms often exhibit variable inference times, potentially causing timing violations in hard real-time systems. Edge computing architectures can mitigate this issue by processing data closer to sensors.
Power consumption emerges as increasingly important in battery-operated devices. Kalman filters typically consume minimal power, while machine learning inference can drain batteries rapidly without optimization. Specialized hardware like Google's Edge TPU or NVIDIA's Jetson platforms offer energy-efficient alternatives for deploying machine learning models.
Implementation complexity also differs significantly. Kalman filters require precise mathematical modeling but follow well-established implementation patterns. Machine learning deployment involves complex toolchains including model conversion, optimization, and runtime integration. Frameworks like TensorFlow Lite and ONNX Runtime have simplified this process but still require substantial expertise.
Hybrid approaches combining both technologies often provide optimal solutions, with Kalman filters handling time-critical state estimation while machine learning algorithms process higher-level information with less stringent timing requirements.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!