How To Harness Kalman Filter For Real-Time Feedback Control
SEP 9, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter Evolution and Implementation Goals
The Kalman filter, developed by Rudolf E. Kalman in 1960, represents a significant milestone in control theory and signal processing. Originally designed for aerospace applications during the Apollo program, this mathematical algorithm has evolved into a cornerstone technology for state estimation in dynamic systems characterized by uncertainty. The filter's fundamental principle lies in its recursive approach to estimating a system's state by combining measurement data with prior knowledge about the system and measurement devices.
Over the decades, the Kalman filter has undergone substantial evolution. The Extended Kalman Filter (EKF) emerged to address nonlinear system dynamics through linearization techniques. Subsequently, the Unscented Kalman Filter (UKF) was developed to better handle strong nonlinearities by using deterministic sampling approaches. More recent innovations include the Ensemble Kalman Filter (EnKF) for high-dimensional systems and the Cubature Kalman Filter (CKF) for improved numerical stability.
The implementation goals for Kalman filters in real-time feedback control systems are multifaceted. Primary objectives include achieving robust state estimation under noisy conditions, maintaining computational efficiency for real-time applications, and ensuring adaptability to changing system dynamics. These goals are particularly critical in applications requiring high precision control under uncertainty, such as autonomous vehicles, robotics, and industrial automation systems.
From a technical perspective, modern Kalman filter implementations aim to optimize the balance between estimation accuracy and computational overhead. This involves careful tuning of process and measurement noise covariance matrices, implementation of efficient matrix operations, and development of adaptive mechanisms that can adjust filter parameters in response to changing conditions.
Another key implementation goal involves the integration of Kalman filters with complementary technologies. This includes fusion with machine learning techniques for improved parameter estimation, integration with model predictive control frameworks for enhanced control performance, and implementation on specialized hardware such as FPGAs or GPUs for accelerated processing in time-critical applications.
Looking forward, the technical trajectory of Kalman filtering points toward increased robustness against model uncertainties, improved handling of non-Gaussian noise distributions, and enhanced capabilities for distributed and federated implementations in networked control systems. These advancements will further expand the utility of Kalman filters across diverse application domains while maintaining their fundamental role in optimal state estimation for feedback control.
Over the decades, the Kalman filter has undergone substantial evolution. The Extended Kalman Filter (EKF) emerged to address nonlinear system dynamics through linearization techniques. Subsequently, the Unscented Kalman Filter (UKF) was developed to better handle strong nonlinearities by using deterministic sampling approaches. More recent innovations include the Ensemble Kalman Filter (EnKF) for high-dimensional systems and the Cubature Kalman Filter (CKF) for improved numerical stability.
The implementation goals for Kalman filters in real-time feedback control systems are multifaceted. Primary objectives include achieving robust state estimation under noisy conditions, maintaining computational efficiency for real-time applications, and ensuring adaptability to changing system dynamics. These goals are particularly critical in applications requiring high precision control under uncertainty, such as autonomous vehicles, robotics, and industrial automation systems.
From a technical perspective, modern Kalman filter implementations aim to optimize the balance between estimation accuracy and computational overhead. This involves careful tuning of process and measurement noise covariance matrices, implementation of efficient matrix operations, and development of adaptive mechanisms that can adjust filter parameters in response to changing conditions.
Another key implementation goal involves the integration of Kalman filters with complementary technologies. This includes fusion with machine learning techniques for improved parameter estimation, integration with model predictive control frameworks for enhanced control performance, and implementation on specialized hardware such as FPGAs or GPUs for accelerated processing in time-critical applications.
Looking forward, the technical trajectory of Kalman filtering points toward increased robustness against model uncertainties, improved handling of non-Gaussian noise distributions, and enhanced capabilities for distributed and federated implementations in networked control systems. These advancements will further expand the utility of Kalman filters across diverse application domains while maintaining their fundamental role in optimal state estimation for feedback control.
Market Applications for Real-Time Feedback Control Systems
Real-time feedback control systems powered by Kalman filtering technology have penetrated numerous market sectors, revolutionizing precision control applications across industries. The automotive sector represents one of the largest markets, with advanced driver assistance systems (ADAS) and autonomous vehicles heavily relying on Kalman filter implementations for sensor fusion, position tracking, and motion prediction. This market segment is projected to grow substantially as vehicle autonomy levels increase, with particular emphasis on urban mobility solutions and commercial fleet management.
The aerospace and defense industries constitute another significant application domain, where Kalman filters enable precise navigation, target tracking, and guidance systems. Military applications include unmanned aerial vehicles (UAVs), missile guidance systems, and radar tracking, while commercial aviation utilizes these algorithms for flight control systems and air traffic management. Space exploration missions depend on Kalman filtering for spacecraft attitude determination and orbital mechanics calculations.
Industrial automation represents a rapidly expanding market for Kalman filter-based control systems. Manufacturing facilities implement these algorithms in robotics for precise movement control, in process automation for maintaining optimal operating conditions, and in quality control systems for real-time defect detection. The integration with Industry 4.0 initiatives has accelerated adoption rates as factories transition toward more intelligent and responsive production environments.
Consumer electronics manufacturers have increasingly incorporated Kalman filtering into products ranging from smartphones to wearable devices. Applications include image stabilization in cameras, motion sensing in gaming peripherals, and activity tracking in fitness devices. The miniaturization of sensors and increased computational capabilities of mobile processors have expanded implementation possibilities in this sector.
Healthcare applications represent an emerging high-value market, with Kalman filters enabling precise control in medical robotics, patient monitoring systems, and diagnostic equipment. Surgical robots benefit from enhanced motion stability, while monitoring systems leverage these algorithms for more accurate vital sign tracking and predictive analytics.
Smart infrastructure and urban management systems constitute another growth area, with applications in traffic control, energy grid management, and environmental monitoring. These systems utilize Kalman filtering to process sensor data from distributed networks, enabling more efficient resource allocation and responsive urban services.
The financial technology sector has also adopted Kalman filtering techniques for algorithmic trading, risk assessment, and fraud detection systems, where real-time processing of market signals requires sophisticated filtering of noise from meaningful patterns.
The aerospace and defense industries constitute another significant application domain, where Kalman filters enable precise navigation, target tracking, and guidance systems. Military applications include unmanned aerial vehicles (UAVs), missile guidance systems, and radar tracking, while commercial aviation utilizes these algorithms for flight control systems and air traffic management. Space exploration missions depend on Kalman filtering for spacecraft attitude determination and orbital mechanics calculations.
Industrial automation represents a rapidly expanding market for Kalman filter-based control systems. Manufacturing facilities implement these algorithms in robotics for precise movement control, in process automation for maintaining optimal operating conditions, and in quality control systems for real-time defect detection. The integration with Industry 4.0 initiatives has accelerated adoption rates as factories transition toward more intelligent and responsive production environments.
Consumer electronics manufacturers have increasingly incorporated Kalman filtering into products ranging from smartphones to wearable devices. Applications include image stabilization in cameras, motion sensing in gaming peripherals, and activity tracking in fitness devices. The miniaturization of sensors and increased computational capabilities of mobile processors have expanded implementation possibilities in this sector.
Healthcare applications represent an emerging high-value market, with Kalman filters enabling precise control in medical robotics, patient monitoring systems, and diagnostic equipment. Surgical robots benefit from enhanced motion stability, while monitoring systems leverage these algorithms for more accurate vital sign tracking and predictive analytics.
Smart infrastructure and urban management systems constitute another growth area, with applications in traffic control, energy grid management, and environmental monitoring. These systems utilize Kalman filtering to process sensor data from distributed networks, enabling more efficient resource allocation and responsive urban services.
The financial technology sector has also adopted Kalman filtering techniques for algorithmic trading, risk assessment, and fraud detection systems, where real-time processing of market signals requires sophisticated filtering of noise from meaningful patterns.
Current Challenges in Kalman Filter Implementation
Despite the significant advancements in Kalman filter theory and applications, several critical challenges persist in implementing these filters for real-time feedback control systems. One of the primary obstacles is computational complexity, particularly for high-dimensional systems. As state vectors grow in size, the matrix operations required for Kalman filtering become increasingly demanding, creating significant computational overhead that can compromise real-time performance on resource-constrained platforms such as embedded systems or mobile devices.
Model uncertainty presents another substantial challenge. The Kalman filter fundamentally relies on accurate system models, yet real-world systems rarely conform perfectly to mathematical representations. Discrepancies between the actual system dynamics and the model used in filter design can lead to suboptimal estimation performance or even filter divergence, where estimation errors grow unbounded over time.
Nonlinearity handling remains problematic despite extensions like the Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF). The linearization approach in EKF introduces approximation errors that can accumulate in highly nonlinear systems, while UKF, though more robust, incurs additional computational costs that may be prohibitive for real-time applications requiring high update rates.
Tuning difficulties constitute a significant practical challenge. The performance of Kalman filters depends critically on appropriate noise covariance matrices, which are often difficult to determine accurately in practice. Improper tuning can result in filters that are either too sluggish to track rapid changes or overly sensitive to measurement noise, compromising control system stability.
Numerical stability issues frequently arise in implementation, particularly with ill-conditioned covariance matrices. Round-off errors can accumulate during recursive updates, potentially leading to non-positive definite covariance matrices that violate the mathematical foundations of the filter and cause algorithm failure.
Real-time constraints impose perhaps the most stringent limitations. Many control applications require update rates of hundreds or thousands of Hertz, leaving milliseconds or microseconds for computation. Meeting these timing requirements while maintaining estimation accuracy presents a fundamental trade-off that engineers must carefully navigate.
Sensor fusion complexity increases with the number and diversity of sensors. Synchronizing measurements with different sampling rates, handling communication delays, and managing sensor failures add layers of complexity to Kalman filter implementations in multi-sensor environments typical of modern control systems.
Model uncertainty presents another substantial challenge. The Kalman filter fundamentally relies on accurate system models, yet real-world systems rarely conform perfectly to mathematical representations. Discrepancies between the actual system dynamics and the model used in filter design can lead to suboptimal estimation performance or even filter divergence, where estimation errors grow unbounded over time.
Nonlinearity handling remains problematic despite extensions like the Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF). The linearization approach in EKF introduces approximation errors that can accumulate in highly nonlinear systems, while UKF, though more robust, incurs additional computational costs that may be prohibitive for real-time applications requiring high update rates.
Tuning difficulties constitute a significant practical challenge. The performance of Kalman filters depends critically on appropriate noise covariance matrices, which are often difficult to determine accurately in practice. Improper tuning can result in filters that are either too sluggish to track rapid changes or overly sensitive to measurement noise, compromising control system stability.
Numerical stability issues frequently arise in implementation, particularly with ill-conditioned covariance matrices. Round-off errors can accumulate during recursive updates, potentially leading to non-positive definite covariance matrices that violate the mathematical foundations of the filter and cause algorithm failure.
Real-time constraints impose perhaps the most stringent limitations. Many control applications require update rates of hundreds or thousands of Hertz, leaving milliseconds or microseconds for computation. Meeting these timing requirements while maintaining estimation accuracy presents a fundamental trade-off that engineers must carefully navigate.
Sensor fusion complexity increases with the number and diversity of sensors. Synchronizing measurements with different sampling rates, handling communication delays, and managing sensor failures add layers of complexity to Kalman filter implementations in multi-sensor environments typical of modern control systems.
Contemporary Kalman Filter Integration Methods
01 Kalman filter for real-time control systems
Kalman filters are implemented in real-time control systems to provide optimal state estimation in the presence of noise. These filters recursively process measurement data to estimate the state of a dynamic system, enabling more accurate feedback control. The algorithm combines predictions from system models with actual measurements, weighing each according to their estimated uncertainty, which makes it particularly valuable for applications requiring precise control under noisy conditions.- Kalman filter for navigation and positioning systems: Kalman filters are implemented in navigation and positioning systems to provide real-time feedback control by accurately estimating position, velocity, and orientation. These systems use sensor fusion techniques to combine data from multiple sources such as GPS, inertial measurement units (IMUs), and other sensors to reduce noise and improve accuracy. The adaptive nature of Kalman filtering allows for continuous adjustment of navigation parameters based on real-time measurements, making it particularly valuable for autonomous vehicles, drones, and precision navigation applications.
- Kalman filter in industrial process control: In industrial automation and manufacturing, Kalman filters are employed for real-time feedback control of complex processes. These implementations help in monitoring and controlling production parameters, optimizing manufacturing processes, and maintaining quality control. The filter's predictive capabilities allow for anticipating system behavior and making proactive adjustments to process variables. This approach is particularly effective in environments with multiple variables and noise factors, where traditional control methods might be insufficient for maintaining precise control.
- Kalman filter for communication systems: Kalman filtering techniques are applied in communication systems to enhance signal quality and maintain reliable connections through real-time feedback control. These implementations help in channel estimation, signal tracking, and adaptive modulation in wireless networks. The filter's ability to predict and correct signal parameters allows for dynamic adjustment of transmission characteristics based on changing channel conditions. This approach is particularly valuable in mobile communications, satellite systems, and other scenarios where signal conditions vary rapidly.
- Kalman filter in financial and economic systems: Kalman filters are implemented in financial technology and economic systems to provide real-time feedback control for trading algorithms, risk assessment, and market prediction. These applications use the filter's ability to process noisy market data and extract meaningful trends for decision-making. The adaptive nature of Kalman filtering allows financial systems to respond dynamically to changing market conditions, optimize portfolio management, and improve forecasting accuracy. This approach is particularly valuable in high-frequency trading, algorithmic investment strategies, and economic forecasting models.
- Advanced Kalman filter implementations for complex control systems: Advanced implementations of Kalman filters, including extended, unscented, and ensemble variants, are used in complex control systems requiring sophisticated real-time feedback. These implementations address nonlinear system dynamics, non-Gaussian noise distributions, and multi-modal state estimation challenges. They enable more accurate state estimation and prediction in highly complex environments such as robotics, aerospace systems, and advanced manufacturing. These sophisticated Kalman filter variants provide robust performance in scenarios where traditional linear Kalman filters would be insufficient, allowing for precise control in highly dynamic and uncertain environments.
02 Adaptive Kalman filtering techniques
Adaptive Kalman filtering techniques dynamically adjust filter parameters based on changing system conditions. These methods modify the filter's behavior in real-time to maintain optimal performance when system dynamics or noise characteristics change. By continuously updating covariance matrices and noise models, adaptive Kalman filters provide more robust state estimation for feedback control systems operating in variable environments, improving control stability and accuracy.Expand Specific Solutions03 Network-based distributed Kalman filtering
Network-based distributed Kalman filtering enables real-time feedback control across multiple interconnected systems. This approach distributes the computational load of state estimation across networked nodes while maintaining estimation coherence. By sharing measurement data and state estimates between nodes, these systems can achieve coordinated control of complex distributed processes while minimizing communication overhead and maintaining robustness against network delays or failures.Expand Specific Solutions04 Kalman filtering for autonomous navigation and positioning
Kalman filtering techniques are applied to autonomous navigation and positioning systems to provide real-time feedback for trajectory control. These implementations fuse data from multiple sensors such as GPS, IMU, and vision systems to accurately estimate position, velocity, and orientation. The filtered state estimates enable precise path following, obstacle avoidance, and stabilization in autonomous vehicles, drones, and robotic systems operating in dynamic environments.Expand Specific Solutions05 Kalman filter applications in financial and predictive systems
Kalman filtering is implemented in financial and predictive control systems to provide real-time feedback for decision-making processes. These applications use the filter to estimate hidden states in time-series data, enabling more accurate forecasting and anomaly detection. By continuously updating predictions based on new observations, these systems can adapt to changing market conditions, optimize resource allocation, and implement predictive control strategies with minimal latency.Expand Specific Solutions
Leading Organizations in Kalman Filter Technology
The Kalman Filter real-time feedback control market is currently in a growth phase, with increasing adoption across industrial automation, aerospace, and automotive sectors. The market is projected to expand significantly as demand for precise control systems rises in autonomous vehicles and robotics applications. Leading players include Siemens AG and Robert Bosch GmbH, who have integrated advanced Kalman filtering into their industrial automation platforms, while aerospace specialists like Safran SA and Airbus Operations GmbH utilize these algorithms for flight control systems. Automotive manufacturers BMW and Ford are implementing Kalman filters in ADAS technologies. Academic institutions such as Zhejiang University and Harbin Engineering University are contributing significant research, collaborating with industry to bridge theoretical advances with practical implementations.
Siemens AG
Technical Solution: Siemens has developed advanced Kalman filter implementations for industrial automation and control systems. Their approach integrates Extended Kalman Filters (EKF) with model predictive control frameworks to enhance real-time feedback in manufacturing processes. The company's SIMATIC automation platform incorporates Kalman filtering algorithms that adaptively estimate system states while accounting for measurement noise and system uncertainties[1]. Siemens has particularly focused on distributed Kalman filter architectures that enable multi-sensor fusion across industrial networks, allowing for more robust state estimation in complex manufacturing environments. Their implementation includes specialized hardware acceleration for Kalman computations, reducing latency to sub-millisecond levels for critical control applications[3]. Siemens has also pioneered the integration of Kalman filters with digital twins, enabling predictive maintenance and process optimization through real-time comparison between actual system behavior and simulated models.
Strengths: Siemens' implementation excels in industrial-grade reliability with fault-tolerant architectures and seamless integration with existing automation infrastructure. Their distributed processing approach enables scalability across large industrial systems. Weaknesses: The solutions often require significant computational resources and specialized hardware, potentially limiting deployment in resource-constrained environments. Implementation complexity can necessitate specialized expertise for configuration and maintenance.
Robert Bosch GmbH
Technical Solution: Bosch has developed sophisticated Kalman filter implementations primarily focused on automotive and IoT applications. Their approach centers on highly optimized Unscented Kalman Filters (UKF) that handle the non-linearities inherent in vehicle dynamics and sensor systems. Bosch's implementation features adaptive noise covariance estimation that automatically adjusts to changing environmental conditions, crucial for maintaining control stability in diverse operating scenarios[2]. The company has integrated these filters into their vehicle stability control systems, combining inertial measurement units with wheel speed sensors and steering angle data to provide precise vehicle state estimation. Bosch's architecture employs a multi-rate Kalman filter design that processes different sensor inputs at their native frequencies while maintaining a consistent state estimate update rate[4]. Their implementation includes specialized fixed-point arithmetic optimizations for deployment on automotive-grade microcontrollers, achieving processing times under 2ms even for complex vehicle dynamics models with 12+ state variables.
Strengths: Bosch's implementation offers exceptional robustness against sensor failures and environmental disturbances, with proven performance in safety-critical applications. Their solutions feature highly optimized code for embedded systems with limited computational resources. Weaknesses: The highly specialized nature of their implementations can make adaptation to non-automotive applications challenging. The solutions often require extensive calibration procedures specific to each vehicle platform or application.
Core Algorithms and Mathematical Foundations
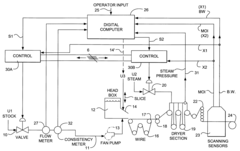
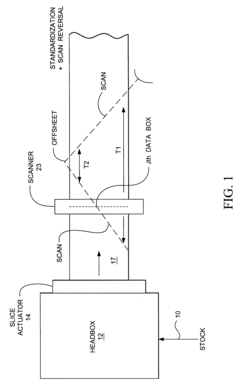
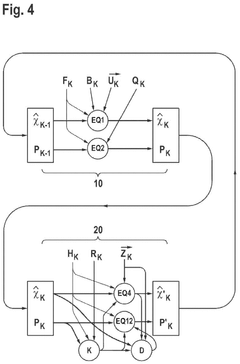
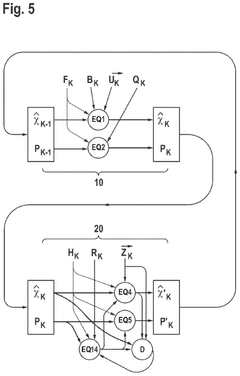
Real time measurement system for a moving web using a Kalman filter algorithm
PatentInactiveUS6493601B1
Innovation
- The implementation of a Kalman filter algorithm that reduces computational complexity by solving the Gauss-Markov equations using a vector representation of the H matrix, rather than a matrix, and treating the exponential matrix as a narrow-banded diagonal matrix, allowing for efficient prediction and update of parameter values for continuous feedback control.
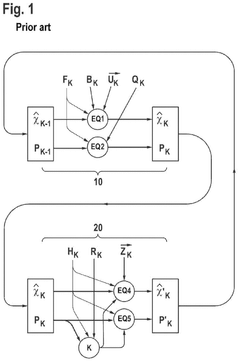
Method for determining at least one system state by means of a Kalman filter
PatentActiveUS12130594B2
Innovation
- A method that estimates system states using a Kalman filter by determining discrepancies between model and measured values, attributing these discrepancies to the reliability of the estimation, and adjusting the estimation uncertainty accordingly, allowing for a direct impact on the reliability of the estimation result.
Computational Resource Requirements
Implementing Kalman filters in real-time feedback control systems demands careful consideration of computational resources to ensure optimal performance. The computational complexity of Kalman filtering primarily scales with the dimensionality of the state vector and measurement vector. For an n-dimensional state vector, the time complexity is approximately O(n³) due to matrix operations, particularly matrix inversions and multiplications. This becomes especially significant in high-dimensional systems where computational efficiency is paramount.
Memory requirements also present challenges, as Kalman filters necessitate storage for state vectors, covariance matrices, and transition matrices. For an n-dimensional state, the memory footprint is approximately O(n²), which can become substantial in complex control applications. Embedded systems with limited RAM must implement optimized versions of the algorithm or consider alternative filtering approaches.
Processing speed requirements vary significantly based on the application domain. High-frequency control loops, such as those in drone stabilization or autonomous vehicle navigation, may require filter updates at rates exceeding 100Hz. This demands either powerful processors or algorithm optimizations to meet real-time constraints. In contrast, slower processes like temperature control systems may operate effectively with update rates below 10Hz, allowing implementation on less powerful hardware.
Hardware acceleration options have become increasingly important for complex implementations. Field-Programmable Gate Arrays (FPGAs) offer significant advantages for Kalman filter implementations, providing parallel processing capabilities that can dramatically reduce computation time for matrix operations. Graphics Processing Units (GPUs) present another acceleration option, particularly beneficial for systems with very high-dimensional state spaces or those requiring multiple concurrent filter instances.
Optimization techniques can substantially reduce resource requirements. Square-root formulations of the Kalman filter improve numerical stability while reducing computational demands. Information filters, mathematically equivalent to Kalman filters, offer computational advantages in systems with more measurements than states. For systems with specific structural properties, specialized variants like the Steady-State Kalman Filter can eliminate the need for costly covariance matrix updates once the filter converges.
Power consumption considerations become critical in battery-operated devices. The computational intensity of Kalman filtering can significantly impact battery life, necessitating careful algorithm optimization and potentially dynamic adjustment of filter parameters based on available power resources. Adaptive implementations that modify update rates or precision based on system dynamics can provide an effective balance between accuracy and resource utilization.
Memory requirements also present challenges, as Kalman filters necessitate storage for state vectors, covariance matrices, and transition matrices. For an n-dimensional state, the memory footprint is approximately O(n²), which can become substantial in complex control applications. Embedded systems with limited RAM must implement optimized versions of the algorithm or consider alternative filtering approaches.
Processing speed requirements vary significantly based on the application domain. High-frequency control loops, such as those in drone stabilization or autonomous vehicle navigation, may require filter updates at rates exceeding 100Hz. This demands either powerful processors or algorithm optimizations to meet real-time constraints. In contrast, slower processes like temperature control systems may operate effectively with update rates below 10Hz, allowing implementation on less powerful hardware.
Hardware acceleration options have become increasingly important for complex implementations. Field-Programmable Gate Arrays (FPGAs) offer significant advantages for Kalman filter implementations, providing parallel processing capabilities that can dramatically reduce computation time for matrix operations. Graphics Processing Units (GPUs) present another acceleration option, particularly beneficial for systems with very high-dimensional state spaces or those requiring multiple concurrent filter instances.
Optimization techniques can substantially reduce resource requirements. Square-root formulations of the Kalman filter improve numerical stability while reducing computational demands. Information filters, mathematically equivalent to Kalman filters, offer computational advantages in systems with more measurements than states. For systems with specific structural properties, specialized variants like the Steady-State Kalman Filter can eliminate the need for costly covariance matrix updates once the filter converges.
Power consumption considerations become critical in battery-operated devices. The computational intensity of Kalman filtering can significantly impact battery life, necessitating careful algorithm optimization and potentially dynamic adjustment of filter parameters based on available power resources. Adaptive implementations that modify update rates or precision based on system dynamics can provide an effective balance between accuracy and resource utilization.
System Stability and Robustness Analysis
When implementing Kalman filters in real-time feedback control systems, stability and robustness analysis becomes paramount to ensure reliable operation under varying conditions. The fundamental stability of Kalman filter-based control systems depends on the eigenvalues of the closed-loop system matrix, which must lie within the unit circle in the complex plane. This requirement ensures that estimation errors remain bounded over time, preventing divergence that could lead to catastrophic system failures.
Robustness in Kalman filter implementations refers to the system's ability to maintain performance despite model uncertainties, parameter variations, and external disturbances. The filter's sensitivity to modeling errors can be quantified through condition numbers of the error covariance matrices. Lower condition numbers generally indicate better numerical stability and robustness against perturbations in the system model.
Process and measurement noise covariance matrices (Q and R respectively) play critical roles in determining system robustness. Overestimating process noise can lead to excessive filter responsiveness and potential instability, while underestimating it may result in sluggish response to actual state changes. Similarly, inappropriate measurement noise characterization can cause the filter to either overreact to sensor noise or insufficiently respond to genuine measurements.
Monte Carlo simulations provide valuable insights into stability margins by testing the filter's performance across thousands of randomized scenarios. These simulations can reveal edge cases where the filter might become unstable, allowing engineers to implement safeguards before deployment. Statistical analysis of these simulation results helps quantify the probability of filter divergence under various operating conditions.
H-infinity techniques offer complementary approaches to traditional Kalman filtering when robustness is the primary concern. While Kalman filters are optimal for Gaussian noise, H-infinity filters minimize the worst-case estimation error, providing guaranteed performance bounds under bounded disturbances. Hybrid approaches combining Kalman and H-infinity methodologies often yield control systems with both good average performance and strong robustness guarantees.
For real-time applications, numerical stability becomes especially important as computational resources may be limited. Square-root formulations of the Kalman filter can significantly improve numerical conditioning, ensuring stable operation even with finite-precision arithmetic. Joseph's form of the covariance update equation, though computationally more intensive, provides enhanced numerical stability compared to the standard form.
Robustness in Kalman filter implementations refers to the system's ability to maintain performance despite model uncertainties, parameter variations, and external disturbances. The filter's sensitivity to modeling errors can be quantified through condition numbers of the error covariance matrices. Lower condition numbers generally indicate better numerical stability and robustness against perturbations in the system model.
Process and measurement noise covariance matrices (Q and R respectively) play critical roles in determining system robustness. Overestimating process noise can lead to excessive filter responsiveness and potential instability, while underestimating it may result in sluggish response to actual state changes. Similarly, inappropriate measurement noise characterization can cause the filter to either overreact to sensor noise or insufficiently respond to genuine measurements.
Monte Carlo simulations provide valuable insights into stability margins by testing the filter's performance across thousands of randomized scenarios. These simulations can reveal edge cases where the filter might become unstable, allowing engineers to implement safeguards before deployment. Statistical analysis of these simulation results helps quantify the probability of filter divergence under various operating conditions.
H-infinity techniques offer complementary approaches to traditional Kalman filtering when robustness is the primary concern. While Kalman filters are optimal for Gaussian noise, H-infinity filters minimize the worst-case estimation error, providing guaranteed performance bounds under bounded disturbances. Hybrid approaches combining Kalman and H-infinity methodologies often yield control systems with both good average performance and strong robustness guarantees.
For real-time applications, numerical stability becomes especially important as computational resources may be limited. Square-root formulations of the Kalman filter can significantly improve numerical conditioning, ensuring stable operation even with finite-precision arithmetic. Joseph's form of the covariance update equation, though computationally more intensive, provides enhanced numerical stability compared to the standard form.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!