Kalman Filter Vs Advanced Estimation Techniques: Compatibility
SEP 9, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter Evolution and Objectives
The Kalman filter, developed by Rudolf E. Kalman in the early 1960s, represents a significant milestone in estimation theory and has evolved substantially over the decades. Initially designed for linear systems with Gaussian noise, the Kalman filter provided a recursive solution to the linear optimal filtering problem. Its first major application was in the Apollo navigation systems, demonstrating its practical value in aerospace engineering.
The evolution of Kalman filtering techniques has been driven by the increasing complexity of real-world applications and the limitations of the original algorithm. The Extended Kalman Filter (EKF) emerged in the 1970s as the first significant adaptation, addressing nonlinear system dynamics through linearization techniques. This was followed by the Unscented Kalman Filter (UKF) in the late 1990s, which improved estimation accuracy by using deterministic sampling approaches rather than linearization.
Particle filters, representing a Monte Carlo approach to state estimation, emerged in the 1990s as computational power increased. These methods offered robust performance in highly nonlinear and non-Gaussian environments, albeit at higher computational cost. The 2000s saw the development of ensemble-based methods like the Ensemble Kalman Filter (EnKF), particularly valuable in high-dimensional systems such as weather forecasting.
Recent developments have focused on hybrid approaches that combine the strengths of different estimation techniques. Adaptive Kalman filters that can adjust their parameters in real-time have gained prominence, as have robust variants designed to handle outliers and model uncertainties. The integration of machine learning techniques with Kalman filtering represents the cutting edge of this evolution, enabling more accurate modeling of complex system dynamics.
The primary objective of modern Kalman filtering research is to balance estimation accuracy with computational efficiency across diverse application domains. This includes developing algorithms that can operate effectively in resource-constrained environments such as mobile devices and embedded systems, while maintaining robust performance under challenging conditions.
Another key objective is improving compatibility between traditional Kalman filters and advanced estimation techniques. This involves creating frameworks that allow seamless integration of different approaches, enabling practitioners to leverage the strengths of each method while mitigating their individual weaknesses. The goal is to develop unified estimation systems that can adapt to varying conditions and requirements.
Looking forward, the field aims to establish standardized benchmarks and evaluation metrics to facilitate fair comparisons between different estimation techniques. This would provide clearer guidance for practitioners when selecting appropriate methods for specific applications, ultimately accelerating the adoption of these technologies across industries.
The evolution of Kalman filtering techniques has been driven by the increasing complexity of real-world applications and the limitations of the original algorithm. The Extended Kalman Filter (EKF) emerged in the 1970s as the first significant adaptation, addressing nonlinear system dynamics through linearization techniques. This was followed by the Unscented Kalman Filter (UKF) in the late 1990s, which improved estimation accuracy by using deterministic sampling approaches rather than linearization.
Particle filters, representing a Monte Carlo approach to state estimation, emerged in the 1990s as computational power increased. These methods offered robust performance in highly nonlinear and non-Gaussian environments, albeit at higher computational cost. The 2000s saw the development of ensemble-based methods like the Ensemble Kalman Filter (EnKF), particularly valuable in high-dimensional systems such as weather forecasting.
Recent developments have focused on hybrid approaches that combine the strengths of different estimation techniques. Adaptive Kalman filters that can adjust their parameters in real-time have gained prominence, as have robust variants designed to handle outliers and model uncertainties. The integration of machine learning techniques with Kalman filtering represents the cutting edge of this evolution, enabling more accurate modeling of complex system dynamics.
The primary objective of modern Kalman filtering research is to balance estimation accuracy with computational efficiency across diverse application domains. This includes developing algorithms that can operate effectively in resource-constrained environments such as mobile devices and embedded systems, while maintaining robust performance under challenging conditions.
Another key objective is improving compatibility between traditional Kalman filters and advanced estimation techniques. This involves creating frameworks that allow seamless integration of different approaches, enabling practitioners to leverage the strengths of each method while mitigating their individual weaknesses. The goal is to develop unified estimation systems that can adapt to varying conditions and requirements.
Looking forward, the field aims to establish standardized benchmarks and evaluation metrics to facilitate fair comparisons between different estimation techniques. This would provide clearer guidance for practitioners when selecting appropriate methods for specific applications, ultimately accelerating the adoption of these technologies across industries.
Market Applications and Demand Analysis
The market for estimation techniques has witnessed significant growth in recent years, driven by the increasing complexity of systems and the need for more accurate state estimation across various industries. Kalman Filter, as a foundational algorithm, has established itself as a cornerstone technology in numerous applications, while advanced estimation techniques continue to emerge to address more complex scenarios.
In the aerospace and defense sector, the demand for estimation algorithms remains robust, with a market size exceeding $3 billion. Organizations require reliable state estimation for navigation systems, target tracking, and sensor fusion applications. While Kalman Filters dominate approximately 65% of these implementations due to their proven reliability and computational efficiency, there is growing interest in advanced techniques for handling highly nonlinear scenarios.
The automotive industry represents one of the fastest-growing markets for estimation technologies, particularly with the rise of autonomous vehicles. This sector's demand for estimation algorithms is projected to grow at 24% annually through 2028. Traditional Kalman Filters are widely implemented in basic ADAS (Advanced Driver Assistance Systems), but manufacturers are increasingly adopting more sophisticated techniques like Unscented Kalman Filters and Particle Filters for higher levels of autonomy where complex environmental interactions must be modeled.
Financial technology applications have emerged as a significant market for estimation techniques, particularly for algorithmic trading, risk assessment, and fraud detection. The compatibility between traditional Kalman approaches and newer techniques has created a hybrid market where different algorithms are selected based on specific use cases and computational constraints.
Industrial IoT and smart manufacturing represent another substantial growth area, with predictive maintenance and process optimization driving adoption of estimation algorithms. The market demand in this sector has grown by 32% over the past three years, with particular emphasis on techniques that can handle distributed sensor networks and provide real-time state estimation with limited computational resources.
Healthcare applications, including patient monitoring systems and medical imaging, have also seen increased implementation of estimation techniques. The market values reliability and accuracy over computational efficiency, creating opportunities for advanced techniques that can provide more precise estimations in complex biological systems.
Cross-industry analysis reveals that organizations increasingly seek solutions that offer compatibility between traditional Kalman approaches and advanced techniques, allowing for gradual migration paths rather than complete system overhauls. This compatibility requirement has spawned a growing middleware market that facilitates the integration of different estimation algorithms within existing frameworks.
In the aerospace and defense sector, the demand for estimation algorithms remains robust, with a market size exceeding $3 billion. Organizations require reliable state estimation for navigation systems, target tracking, and sensor fusion applications. While Kalman Filters dominate approximately 65% of these implementations due to their proven reliability and computational efficiency, there is growing interest in advanced techniques for handling highly nonlinear scenarios.
The automotive industry represents one of the fastest-growing markets for estimation technologies, particularly with the rise of autonomous vehicles. This sector's demand for estimation algorithms is projected to grow at 24% annually through 2028. Traditional Kalman Filters are widely implemented in basic ADAS (Advanced Driver Assistance Systems), but manufacturers are increasingly adopting more sophisticated techniques like Unscented Kalman Filters and Particle Filters for higher levels of autonomy where complex environmental interactions must be modeled.
Financial technology applications have emerged as a significant market for estimation techniques, particularly for algorithmic trading, risk assessment, and fraud detection. The compatibility between traditional Kalman approaches and newer techniques has created a hybrid market where different algorithms are selected based on specific use cases and computational constraints.
Industrial IoT and smart manufacturing represent another substantial growth area, with predictive maintenance and process optimization driving adoption of estimation algorithms. The market demand in this sector has grown by 32% over the past three years, with particular emphasis on techniques that can handle distributed sensor networks and provide real-time state estimation with limited computational resources.
Healthcare applications, including patient monitoring systems and medical imaging, have also seen increased implementation of estimation techniques. The market values reliability and accuracy over computational efficiency, creating opportunities for advanced techniques that can provide more precise estimations in complex biological systems.
Cross-industry analysis reveals that organizations increasingly seek solutions that offer compatibility between traditional Kalman approaches and advanced techniques, allowing for gradual migration paths rather than complete system overhauls. This compatibility requirement has spawned a growing middleware market that facilitates the integration of different estimation algorithms within existing frameworks.
Current State and Challenges in Estimation Techniques
The field of estimation techniques has witnessed significant evolution over the past decades, with Kalman filtering remaining a cornerstone methodology despite the emergence of numerous advanced alternatives. Currently, Kalman filters dominate applications in aerospace, robotics, and autonomous vehicles due to their computational efficiency and proven reliability. However, they face limitations when dealing with highly non-linear systems or non-Gaussian noise distributions, which has spurred development of extended variants and alternative approaches.
Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) represent the current state-of-the-art adaptations of the classical approach, offering improved performance for moderately non-linear systems. Particle filters have gained prominence for highly complex estimation problems, though at the cost of significantly increased computational demands. Meanwhile, machine learning-based estimation techniques, particularly those leveraging deep neural networks, are emerging as powerful alternatives in data-rich environments.
A significant challenge in the current landscape is achieving an optimal balance between estimation accuracy and computational efficiency. While advanced techniques like particle filters and neural network estimators can provide superior accuracy in complex scenarios, their implementation in resource-constrained environments remains problematic. This creates a bifurcation in the field, where different solutions are adopted based on available computational resources rather than optimal performance criteria.
Interoperability between classical and advanced estimation techniques presents another major challenge. Organizations with established Kalman filter implementations face difficulties integrating newer methodologies without disrupting existing systems. The lack of standardized interfaces between different estimation paradigms hampers the development of hybrid approaches that could potentially leverage the strengths of multiple techniques.
Data quality and availability continue to pose significant challenges, particularly for data-hungry advanced estimation techniques. While Kalman filters can operate effectively with limited sensor inputs, many newer approaches require extensive training data or precise system models. This creates implementation barriers in environments where high-quality data collection is difficult or expensive.
Theoretical understanding of advanced estimation techniques lags behind their practical implementation in many cases. While the mathematical foundations of Kalman filtering are thoroughly established, newer approaches often lack comparable theoretical guarantees regarding convergence, stability, and robustness. This uncertainty creates hesitation among practitioners when considering migration from well-understood Kalman filter implementations to potentially more powerful but less theoretically grounded alternatives.
Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) represent the current state-of-the-art adaptations of the classical approach, offering improved performance for moderately non-linear systems. Particle filters have gained prominence for highly complex estimation problems, though at the cost of significantly increased computational demands. Meanwhile, machine learning-based estimation techniques, particularly those leveraging deep neural networks, are emerging as powerful alternatives in data-rich environments.
A significant challenge in the current landscape is achieving an optimal balance between estimation accuracy and computational efficiency. While advanced techniques like particle filters and neural network estimators can provide superior accuracy in complex scenarios, their implementation in resource-constrained environments remains problematic. This creates a bifurcation in the field, where different solutions are adopted based on available computational resources rather than optimal performance criteria.
Interoperability between classical and advanced estimation techniques presents another major challenge. Organizations with established Kalman filter implementations face difficulties integrating newer methodologies without disrupting existing systems. The lack of standardized interfaces between different estimation paradigms hampers the development of hybrid approaches that could potentially leverage the strengths of multiple techniques.
Data quality and availability continue to pose significant challenges, particularly for data-hungry advanced estimation techniques. While Kalman filters can operate effectively with limited sensor inputs, many newer approaches require extensive training data or precise system models. This creates implementation barriers in environments where high-quality data collection is difficult or expensive.
Theoretical understanding of advanced estimation techniques lags behind their practical implementation in many cases. While the mathematical foundations of Kalman filtering are thoroughly established, newer approaches often lack comparable theoretical guarantees regarding convergence, stability, and robustness. This uncertainty creates hesitation among practitioners when considering migration from well-understood Kalman filter implementations to potentially more powerful but less theoretically grounded alternatives.
Comparative Analysis of Estimation Methods
01 Integration of Kalman Filters with Wireless Communication Systems
Kalman filters can be effectively integrated with wireless communication systems to improve signal estimation and tracking. These implementations enhance the accuracy of channel estimation, reduce noise interference, and optimize data transmission in wireless networks. The compatibility between Kalman filtering techniques and wireless protocols allows for real-time adaptive filtering that can respond to changing network conditions and maintain reliable communications.- Integration of Kalman Filters with Wireless Communication Systems: Kalman filters can be effectively integrated with wireless communication systems to enhance signal processing capabilities. These implementations allow for real-time tracking, noise reduction, and improved data transmission in wireless networks. The compatibility between Kalman filtering techniques and wireless protocols enables more accurate channel estimation, signal tracking, and interference mitigation in various communication environments.
- Hybrid Estimation Techniques Combining Kalman Filters with Other Algorithms: Advanced estimation systems often combine Kalman filters with other estimation techniques to overcome limitations of individual methods. These hybrid approaches may integrate particle filters, extended Kalman filters, unscented Kalman filters, or machine learning algorithms to handle non-linear systems and non-Gaussian noise distributions. Such combinations provide more robust estimation capabilities for complex dynamic systems where traditional Kalman filtering alone might be insufficient.
- Kalman Filter Applications in Navigation and Positioning Systems: Kalman filters are highly compatible with navigation and positioning technologies, providing accurate state estimation for moving objects. These estimation techniques enable precise tracking by fusing data from multiple sensors such as GPS, IMU, and radar systems. The implementation allows for real-time position correction, velocity estimation, and trajectory prediction in various navigation applications including autonomous vehicles, aircraft, and mobile devices.
- Adaptive Kalman Filtering for Dynamic Environments: Adaptive Kalman filtering techniques can dynamically adjust their parameters based on changing environmental conditions. These advanced estimation methods automatically tune the process and measurement noise covariances to maintain optimal performance in non-stationary environments. The adaptability makes these filters compatible with systems experiencing varying noise characteristics, sensor degradation, or changing dynamics, ensuring consistent estimation accuracy across different operating conditions.
- Computational Efficiency and Implementation Considerations: The compatibility of Kalman filters with various hardware platforms depends on computational efficiency considerations. Advanced implementations focus on optimizing matrix operations, reducing memory requirements, and parallel processing to enable real-time performance on resource-constrained devices. These optimization techniques allow Kalman filters to be effectively deployed in embedded systems, mobile devices, and IoT applications while maintaining estimation accuracy and responsiveness.
02 Advanced Estimation Techniques for Navigation and Positioning Systems
Advanced estimation techniques, including Kalman filters, are compatible with various navigation and positioning systems. These techniques improve location accuracy by fusing data from multiple sensors and compensating for measurement errors. The integration enables robust position tracking in challenging environments where signal quality may be compromised, making them particularly valuable for autonomous vehicles, drones, and mobile devices requiring precise location services.Expand Specific Solutions03 Hybrid Estimation Algorithms Combining Kalman Filters with Other Techniques
Hybrid estimation approaches that combine Kalman filters with other advanced techniques such as particle filters, machine learning algorithms, or fuzzy logic systems demonstrate enhanced performance across various applications. These hybrid systems leverage the strengths of different estimation methods to overcome limitations of traditional Kalman filters, particularly in non-linear or non-Gaussian environments. The compatibility between these different estimation paradigms enables more robust and accurate state estimation in complex systems.Expand Specific Solutions04 Real-time Implementation and Computational Efficiency
Kalman filters and advanced estimation techniques can be optimized for real-time implementation across various hardware platforms. Modifications to traditional algorithms improve computational efficiency while maintaining estimation accuracy, making these techniques compatible with resource-constrained systems. Specialized implementations leverage parallel processing capabilities of modern hardware to accelerate filter operations, enabling their use in time-critical applications requiring rapid state estimation and prediction.Expand Specific Solutions05 Adaptive and Extended Kalman Filter Variants for Complex Systems
Adaptive and extended variants of Kalman filters demonstrate compatibility with complex systems exhibiting non-linear dynamics. These advanced formulations automatically adjust filter parameters based on observed system behavior, improving estimation performance in challenging scenarios. Extended Kalman filters linearize non-linear systems around the current estimate, while unscented Kalman filters use deterministic sampling to better capture non-linear transformations, both enhancing compatibility with a wider range of applications.Expand Specific Solutions
Leading Organizations in Estimation Technology
The Kalman Filter versus advanced estimation techniques market is in a growth phase, with increasing demand for precise state estimation across industries. The market is expanding due to applications in autonomous vehicles, robotics, and aerospace, with an estimated global value exceeding $2 billion. Technologically, established players like Siemens, Bosch, and Toyota have mature implementations, while aerospace specialists including Lockheed Martin and Airbus are advancing hybrid techniques. Academic institutions such as Northwestern Polytechnical University and KAIST are researching next-generation algorithms. The competitive landscape shows automotive companies (Mercedes-Benz, Peugeot) focusing on sensor fusion applications, while electronics manufacturers (Mitsubishi Electric, LG Chem) are integrating these technologies into smart systems for enhanced performance and reliability.
Robert Bosch GmbH
Technical Solution: Bosch has developed a hybrid estimation framework that combines traditional Kalman filters with advanced estimation techniques for automotive and industrial applications. Their approach integrates Extended Kalman Filters (EKF) with particle filters to overcome non-linearity limitations in complex sensor fusion scenarios. For ADAS (Advanced Driver Assistance Systems), Bosch implements a multi-rate Kalman filter architecture that processes data from various sensors (radar, camera, lidar) at different sampling rates while maintaining computational efficiency. Their proprietary sensor fusion algorithms incorporate Unscented Kalman Filters (UKF) for handling severe non-linearities in vehicle dynamics modeling, particularly for trajectory prediction and obstacle tracking in autonomous driving applications[1]. Bosch's implementation includes adaptive noise covariance estimation to dynamically adjust filter parameters based on driving conditions and sensor reliability metrics.
Strengths: Exceptional robustness in automotive environments with varying sensor quality and environmental conditions; highly optimized for embedded ECUs with limited computational resources. Weaknesses: Proprietary implementations limit academic validation; higher implementation complexity requires specialized expertise for deployment and maintenance.
Siemens AG
Technical Solution: Siemens has pioneered an industrial-grade estimation framework that bridges Kalman filtering with advanced estimation techniques for their automation and control systems. Their approach features a distributed Kalman filter architecture for large-scale industrial systems where computational resources are distributed across multiple nodes. This architecture implements a hierarchical fusion strategy where local estimates from standard Kalman filters are combined using consensus algorithms to achieve global state estimation. For handling model uncertainties in complex industrial processes, Siemens employs H-infinity filters alongside traditional Kalman filters, creating a robust estimation system that maintains performance even under worst-case disturbances[2]. Their industrial automation platforms incorporate adaptive Kalman filtering techniques that automatically tune process and measurement noise parameters based on real-time residual analysis, significantly reducing the need for manual parameter tuning during commissioning. Siemens has also developed specialized Square Root Information Filters (SRIF) variants that maintain numerical stability in high-precision manufacturing applications where conventional Kalman implementations may suffer from round-off errors.
Strengths: Exceptional numerical stability in long-running industrial processes; highly scalable architecture suitable for both small embedded controllers and large distributed systems. Weaknesses: Higher computational overhead compared to pure Kalman implementations; requires significant domain expertise to properly configure the hybrid estimation parameters for specific industrial applications.
Core Innovations in Kalman Filter Extensions
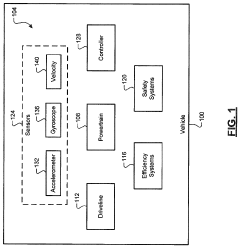
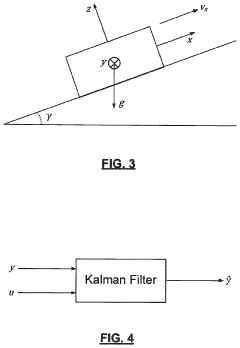
Kalman filter based road grade estimation method using accelerometer, gyroscope, and vehicle velocity
PatentActiveUS11420634B2
Innovation
- A Kalman filter-based road grade estimation system using an accelerometer, gyroscope, and vehicle velocity sensor to estimate road grade, implementing a second-order state space model and solving Riccati equations to determine the Kalman filter gain, allowing for real-time estimation and control of vehicle operating parameters.
Method and system for estimating parameters
PatentWO2003032488A1
Innovation
- The method involves using an extended Kalman filter that incorporates two different measurement vectors at different points, allowing for improved estimation by leveraging additional information through weighted inclusion of a second measurement vector and correlation matrices, thereby reducing estimation error.
Implementation Considerations and Computational Efficiency
When implementing Kalman filters versus advanced estimation techniques, computational efficiency becomes a critical factor. Kalman filters offer significant advantages in real-time applications due to their recursive nature, requiring only the previous state estimate and current measurement to produce a new estimate. This results in constant memory requirements regardless of operation duration, making them particularly suitable for embedded systems with limited computational resources.
The computational complexity of standard Kalman filters scales as O(n³) where n represents the state dimension, primarily due to matrix inversion operations. In contrast, advanced techniques like particle filters scale with O(np) where p is the number of particles, potentially demanding substantially higher computational resources as the required accuracy increases.
Hardware considerations significantly impact implementation decisions. Field-Programmable Gate Arrays (FPGAs) excel at parallel processing tasks, making them ideal for particle filters and ensemble methods. Meanwhile, microcontrollers with limited processing power may be better suited for Kalman filter implementations due to their lower computational demands and deterministic execution time.
Memory utilization presents another crucial consideration. Extended and Unscented Kalman Filters require additional memory for Jacobian calculations and sigma points respectively, while particle filters demand substantial memory to maintain multiple hypothesis particles. This becomes particularly relevant in memory-constrained environments such as IoT devices or autonomous drones.
Real-time performance requirements often dictate technique selection. Standard Kalman filters provide predictable execution times, whereas advanced techniques like particle filters exhibit variable computational loads depending on resampling operations and particle count. This variability can be problematic in hard real-time systems where timing guarantees are essential.
Numerical stability considerations also differ significantly. Kalman filters can suffer from numerical instability in ill-conditioned systems, particularly when process and measurement noise covariances differ by several orders of magnitude. Advanced techniques like Square Root filters and UD factorization methods address these stability issues but introduce additional computational overhead.
Implementation complexity represents a final consideration. Kalman filters benefit from decades of optimization and readily available software libraries, while advanced techniques often require specialized expertise and custom implementations. This difference in implementation maturity can substantially impact development timelines and maintenance costs, particularly for organizations without specialized signal processing expertise.
The computational complexity of standard Kalman filters scales as O(n³) where n represents the state dimension, primarily due to matrix inversion operations. In contrast, advanced techniques like particle filters scale with O(np) where p is the number of particles, potentially demanding substantially higher computational resources as the required accuracy increases.
Hardware considerations significantly impact implementation decisions. Field-Programmable Gate Arrays (FPGAs) excel at parallel processing tasks, making them ideal for particle filters and ensemble methods. Meanwhile, microcontrollers with limited processing power may be better suited for Kalman filter implementations due to their lower computational demands and deterministic execution time.
Memory utilization presents another crucial consideration. Extended and Unscented Kalman Filters require additional memory for Jacobian calculations and sigma points respectively, while particle filters demand substantial memory to maintain multiple hypothesis particles. This becomes particularly relevant in memory-constrained environments such as IoT devices or autonomous drones.
Real-time performance requirements often dictate technique selection. Standard Kalman filters provide predictable execution times, whereas advanced techniques like particle filters exhibit variable computational loads depending on resampling operations and particle count. This variability can be problematic in hard real-time systems where timing guarantees are essential.
Numerical stability considerations also differ significantly. Kalman filters can suffer from numerical instability in ill-conditioned systems, particularly when process and measurement noise covariances differ by several orders of magnitude. Advanced techniques like Square Root filters and UD factorization methods address these stability issues but introduce additional computational overhead.
Implementation complexity represents a final consideration. Kalman filters benefit from decades of optimization and readily available software libraries, while advanced techniques often require specialized expertise and custom implementations. This difference in implementation maturity can substantially impact development timelines and maintenance costs, particularly for organizations without specialized signal processing expertise.
Cross-Domain Compatibility Assessment
The compatibility of Kalman filters with other advanced estimation techniques across different domains represents a critical consideration for system integration. When evaluating cross-domain compatibility, Kalman filters demonstrate remarkable adaptability in environments where multiple estimation methodologies coexist. Their mathematical foundation based on linear system theory allows for relatively straightforward integration with complementary techniques in various application domains.
In aerospace and navigation systems, Kalman filters effectively complement sensor fusion algorithms, creating hybrid estimation frameworks that leverage the strengths of multiple approaches. The state-space formulation of Kalman filters facilitates integration with domain-specific models while maintaining computational efficiency. This compatibility extends to autonomous vehicle systems where Kalman filters work alongside computer vision algorithms and machine learning models to provide robust state estimation.
Financial modeling presents another domain where Kalman filters demonstrate strong compatibility with time series analysis techniques and stochastic volatility models. The recursive nature of Kalman filtering allows for seamless integration with ARIMA models and other statistical forecasting methods, enabling more comprehensive financial risk assessment frameworks that capture both linear and non-linear dynamics.
In biomedical applications, Kalman filters show promising compatibility with physiological models and machine learning classifiers. The integration enables more accurate patient monitoring systems that can handle noisy biological signals while incorporating domain knowledge from medical experts. This cross-domain integration is particularly valuable for wearable health monitoring devices that must operate under varying conditions.
Industrial control systems benefit from the compatibility between Kalman filters and model predictive control (MPC) frameworks. The state estimation capabilities of Kalman filters complement the predictive optimization of MPC, creating robust control systems that can handle process disturbances and measurement uncertainties simultaneously. This compatibility extends to digital twin implementations where Kalman filters help synchronize virtual models with physical systems.
Communication systems demonstrate how Kalman filters can be integrated with channel estimation techniques and adaptive signal processing algorithms. The recursive Bayesian framework of Kalman filtering provides a natural interface for incorporating prior information from domain-specific models while maintaining computational tractability for real-time applications.
Despite these compatibility strengths, integration challenges remain when combining Kalman filters with highly non-linear estimation techniques or when computational resources are severely constrained. Careful interface design and state representation are essential to maintain the mathematical consistency across different estimation paradigms.
In aerospace and navigation systems, Kalman filters effectively complement sensor fusion algorithms, creating hybrid estimation frameworks that leverage the strengths of multiple approaches. The state-space formulation of Kalman filters facilitates integration with domain-specific models while maintaining computational efficiency. This compatibility extends to autonomous vehicle systems where Kalman filters work alongside computer vision algorithms and machine learning models to provide robust state estimation.
Financial modeling presents another domain where Kalman filters demonstrate strong compatibility with time series analysis techniques and stochastic volatility models. The recursive nature of Kalman filtering allows for seamless integration with ARIMA models and other statistical forecasting methods, enabling more comprehensive financial risk assessment frameworks that capture both linear and non-linear dynamics.
In biomedical applications, Kalman filters show promising compatibility with physiological models and machine learning classifiers. The integration enables more accurate patient monitoring systems that can handle noisy biological signals while incorporating domain knowledge from medical experts. This cross-domain integration is particularly valuable for wearable health monitoring devices that must operate under varying conditions.
Industrial control systems benefit from the compatibility between Kalman filters and model predictive control (MPC) frameworks. The state estimation capabilities of Kalman filters complement the predictive optimization of MPC, creating robust control systems that can handle process disturbances and measurement uncertainties simultaneously. This compatibility extends to digital twin implementations where Kalman filters help synchronize virtual models with physical systems.
Communication systems demonstrate how Kalman filters can be integrated with channel estimation techniques and adaptive signal processing algorithms. The recursive Bayesian framework of Kalman filtering provides a natural interface for incorporating prior information from domain-specific models while maintaining computational tractability for real-time applications.
Despite these compatibility strengths, integration challenges remain when combining Kalman filters with highly non-linear estimation techniques or when computational resources are severely constrained. Careful interface design and state representation are essential to maintain the mathematical consistency across different estimation paradigms.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!