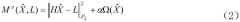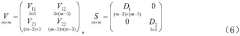How To Achieve Faster Convergence With Kalman Filter
SEP 12, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter Convergence Background and Objectives
The Kalman filter, developed by Rudolf E. Kalman in 1960, represents a significant milestone in estimation theory and has become a cornerstone in modern control systems and signal processing. Originally designed for aerospace applications during the Apollo program, this recursive algorithm has evolved to address complex estimation problems across numerous domains including robotics, navigation, economics, and computer vision.
Convergence speed of Kalman filters remains a critical challenge in real-time applications where computational efficiency directly impacts system performance. The filter's ability to rapidly converge to accurate state estimates determines its practical utility in dynamic environments where conditions change rapidly and decisions must be made with minimal latency.
Recent technological advancements have intensified the need for faster Kalman filter convergence. The proliferation of autonomous vehicles, drones, and IoT devices has created demand for estimation algorithms that can operate under strict time constraints while maintaining high accuracy. Additionally, the increasing complexity of sensor fusion applications, where data from multiple heterogeneous sensors must be integrated seamlessly, further emphasizes the importance of convergence optimization.
The fundamental convergence properties of Kalman filters are governed by several factors including system observability, process and measurement noise characteristics, initial state uncertainty, and the underlying system dynamics. Traditional implementations often face trade-offs between convergence speed and estimation accuracy, particularly in nonlinear systems where extended or unscented variants are employed.
Current research trends focus on several promising directions to enhance convergence performance. These include adaptive parameter tuning techniques, hybrid filtering approaches that combine Kalman filters with other estimation methods, parallelization strategies leveraging modern computing architectures, and machine learning augmentations that optimize filter parameters based on historical data patterns.
The primary technical objectives for improving Kalman filter convergence include: reducing the number of iterations required to reach steady-state performance, minimizing computational overhead while maintaining estimation accuracy, developing robust initialization strategies that accelerate early-stage convergence, and creating adaptive mechanisms that optimize filter performance across varying operating conditions.
This technical exploration aims to comprehensively analyze existing approaches to Kalman filter convergence acceleration, identify fundamental limitations and bottlenecks in current implementations, and propose novel methodologies that can significantly improve convergence characteristics while maintaining the filter's renowned robustness and optimality properties.
Convergence speed of Kalman filters remains a critical challenge in real-time applications where computational efficiency directly impacts system performance. The filter's ability to rapidly converge to accurate state estimates determines its practical utility in dynamic environments where conditions change rapidly and decisions must be made with minimal latency.
Recent technological advancements have intensified the need for faster Kalman filter convergence. The proliferation of autonomous vehicles, drones, and IoT devices has created demand for estimation algorithms that can operate under strict time constraints while maintaining high accuracy. Additionally, the increasing complexity of sensor fusion applications, where data from multiple heterogeneous sensors must be integrated seamlessly, further emphasizes the importance of convergence optimization.
The fundamental convergence properties of Kalman filters are governed by several factors including system observability, process and measurement noise characteristics, initial state uncertainty, and the underlying system dynamics. Traditional implementations often face trade-offs between convergence speed and estimation accuracy, particularly in nonlinear systems where extended or unscented variants are employed.
Current research trends focus on several promising directions to enhance convergence performance. These include adaptive parameter tuning techniques, hybrid filtering approaches that combine Kalman filters with other estimation methods, parallelization strategies leveraging modern computing architectures, and machine learning augmentations that optimize filter parameters based on historical data patterns.
The primary technical objectives for improving Kalman filter convergence include: reducing the number of iterations required to reach steady-state performance, minimizing computational overhead while maintaining estimation accuracy, developing robust initialization strategies that accelerate early-stage convergence, and creating adaptive mechanisms that optimize filter performance across varying operating conditions.
This technical exploration aims to comprehensively analyze existing approaches to Kalman filter convergence acceleration, identify fundamental limitations and bottlenecks in current implementations, and propose novel methodologies that can significantly improve convergence characteristics while maintaining the filter's renowned robustness and optimality properties.
Market Applications and Demand Analysis for Fast Convergence
The market demand for faster convergence in Kalman filter applications has grown exponentially across multiple industries as real-time decision-making becomes increasingly critical. In autonomous vehicles, rapid convergence enables more responsive navigation systems that can adapt to changing road conditions within milliseconds rather than seconds, significantly enhancing safety in unpredictable environments. Market research indicates that automotive manufacturers are willing to invest substantially in sensor fusion technologies that can reduce convergence time by even 10-20%, as this directly translates to improved collision avoidance capabilities.
In financial technology, high-frequency trading platforms require state estimation algorithms that can process market signals with minimal latency. The competitive advantage gained from millisecond improvements in convergence time can translate to millions in additional trading profits. Financial institutions are actively seeking solutions that optimize Kalman filter implementations to achieve convergence in fewer iterations, particularly for complex multi-asset portfolio optimization models.
The aerospace and defense sector represents another significant market segment, where radar tracking systems, missile guidance, and satellite positioning all rely on Kalman filtering. Military applications demand particularly robust solutions that can maintain accuracy while achieving faster convergence under challenging conditions such as electronic countermeasures or rapid target maneuvers.
Consumer electronics manufacturers are incorporating more sophisticated motion sensing and positioning capabilities into smartphones, wearables, and AR/VR devices. These applications are highly constrained by battery life considerations, creating demand for computationally efficient implementations that can achieve rapid convergence while minimizing power consumption. The wearable technology market specifically values algorithms that can accurately track biometric data with minimal initialization time.
Industrial automation and robotics applications require precise motion control and positioning, often in dynamic environments. Manufacturing facilities are increasingly adopting collaborative robots that must respond safely and predictably to human movements, creating demand for filtering solutions that can rapidly converge when estimating human operator intentions and movements.
Healthcare applications present unique requirements, particularly in medical imaging and patient monitoring systems. Real-time processing of physiological signals benefits from faster filter convergence, enabling more responsive interventions in critical care settings. The growing telemedicine sector further amplifies this need, as remote diagnostic systems must quickly establish accurate baselines despite potentially noisy transmission channels.
Market analysis reveals that cross-industry demand for faster Kalman filter convergence is expected to grow as edge computing proliferates and more decision-making processes move closer to sensors. This trend is creating opportunities for specialized hardware accelerators and optimized software implementations that can deliver order-of-magnitude improvements in convergence speed.
In financial technology, high-frequency trading platforms require state estimation algorithms that can process market signals with minimal latency. The competitive advantage gained from millisecond improvements in convergence time can translate to millions in additional trading profits. Financial institutions are actively seeking solutions that optimize Kalman filter implementations to achieve convergence in fewer iterations, particularly for complex multi-asset portfolio optimization models.
The aerospace and defense sector represents another significant market segment, where radar tracking systems, missile guidance, and satellite positioning all rely on Kalman filtering. Military applications demand particularly robust solutions that can maintain accuracy while achieving faster convergence under challenging conditions such as electronic countermeasures or rapid target maneuvers.
Consumer electronics manufacturers are incorporating more sophisticated motion sensing and positioning capabilities into smartphones, wearables, and AR/VR devices. These applications are highly constrained by battery life considerations, creating demand for computationally efficient implementations that can achieve rapid convergence while minimizing power consumption. The wearable technology market specifically values algorithms that can accurately track biometric data with minimal initialization time.
Industrial automation and robotics applications require precise motion control and positioning, often in dynamic environments. Manufacturing facilities are increasingly adopting collaborative robots that must respond safely and predictably to human movements, creating demand for filtering solutions that can rapidly converge when estimating human operator intentions and movements.
Healthcare applications present unique requirements, particularly in medical imaging and patient monitoring systems. Real-time processing of physiological signals benefits from faster filter convergence, enabling more responsive interventions in critical care settings. The growing telemedicine sector further amplifies this need, as remote diagnostic systems must quickly establish accurate baselines despite potentially noisy transmission channels.
Market analysis reveals that cross-industry demand for faster Kalman filter convergence is expected to grow as edge computing proliferates and more decision-making processes move closer to sensors. This trend is creating opportunities for specialized hardware accelerators and optimized software implementations that can deliver order-of-magnitude improvements in convergence speed.
Current Limitations and Technical Challenges in Kalman Filtering
Despite its widespread application, the Kalman Filter faces significant limitations that impede faster convergence in various scenarios. One primary challenge is the assumption of linear system dynamics and Gaussian noise distribution. Real-world systems often exhibit non-linear behaviors, causing the standard Kalman Filter to perform sub-optimally or even diverge. When system dynamics deviate from linearity, the filter's convergence rate deteriorates substantially.
Computational complexity presents another substantial hurdle, particularly in high-dimensional state spaces. As dimensions increase, matrix operations—especially inversions—become computationally expensive, creating bottlenecks in real-time applications. This limitation becomes critical in applications like autonomous vehicles or drone navigation where processing speed directly impacts system safety and performance.
Parameter tuning remains a persistent challenge affecting convergence speed. The filter's performance depends heavily on accurate initialization of state covariance matrices and noise parameters. Suboptimal parameter selection can lead to slow convergence or filter divergence. Currently, many implementations rely on heuristic approaches or extensive trial-and-error processes for parameter tuning, lacking systematic methodologies.
Model mismatch issues further complicate convergence. When the mathematical model used in the filter doesn't accurately represent the actual system dynamics, estimation errors accumulate over time. This discrepancy often manifests as biased estimates or complete filter divergence, particularly problematic in systems with unmodeled dynamics or time-varying characteristics.
Numerical stability issues emerge in practical implementations, especially with limited computational precision. Rounding errors can propagate through iterations, potentially causing the covariance matrix to lose positive definiteness—a critical property for filter stability. These numerical issues become more pronounced in ill-conditioned systems or when dealing with vastly different scales of state variables.
Handling abrupt state changes or outliers poses another significant challenge. The standard Kalman Filter assumes smooth state transitions, making it vulnerable to sudden changes or measurement outliers. Such events can cause temporary divergence or require extended recovery periods, significantly impacting overall convergence speed.
Cross-correlation between process and measurement noise represents a subtle yet impactful limitation. The standard formulation assumes these noise sources are uncorrelated, which is often violated in practical systems. When correlations exist, they introduce estimation biases that slow convergence or prevent the filter from reaching optimal performance.
Computational complexity presents another substantial hurdle, particularly in high-dimensional state spaces. As dimensions increase, matrix operations—especially inversions—become computationally expensive, creating bottlenecks in real-time applications. This limitation becomes critical in applications like autonomous vehicles or drone navigation where processing speed directly impacts system safety and performance.
Parameter tuning remains a persistent challenge affecting convergence speed. The filter's performance depends heavily on accurate initialization of state covariance matrices and noise parameters. Suboptimal parameter selection can lead to slow convergence or filter divergence. Currently, many implementations rely on heuristic approaches or extensive trial-and-error processes for parameter tuning, lacking systematic methodologies.
Model mismatch issues further complicate convergence. When the mathematical model used in the filter doesn't accurately represent the actual system dynamics, estimation errors accumulate over time. This discrepancy often manifests as biased estimates or complete filter divergence, particularly problematic in systems with unmodeled dynamics or time-varying characteristics.
Numerical stability issues emerge in practical implementations, especially with limited computational precision. Rounding errors can propagate through iterations, potentially causing the covariance matrix to lose positive definiteness—a critical property for filter stability. These numerical issues become more pronounced in ill-conditioned systems or when dealing with vastly different scales of state variables.
Handling abrupt state changes or outliers poses another significant challenge. The standard Kalman Filter assumes smooth state transitions, making it vulnerable to sudden changes or measurement outliers. Such events can cause temporary divergence or require extended recovery periods, significantly impacting overall convergence speed.
Cross-correlation between process and measurement noise represents a subtle yet impactful limitation. The standard formulation assumes these noise sources are uncorrelated, which is often violated in practical systems. When correlations exist, they introduce estimation biases that slow convergence or prevent the filter from reaching optimal performance.
Current Approaches to Accelerate Kalman Filter Convergence
01 Adaptive parameter tuning for faster convergence
Techniques for dynamically adjusting Kalman filter parameters to accelerate convergence speed. These methods involve adaptive tuning of process noise covariance, measurement noise covariance, or gain matrices based on real-time performance metrics. By automatically optimizing these parameters during operation, the filter can achieve faster convergence while maintaining stability across varying conditions.- Adaptive parameter tuning for faster convergence: Techniques for dynamically adjusting Kalman filter parameters to accelerate convergence speed. This includes adaptive noise covariance estimation, variable gain scheduling, and real-time parameter optimization based on measurement quality. These methods automatically tune the filter parameters in response to changing conditions, reducing the time needed to reach steady-state estimation accuracy.
- Initial state estimation optimization: Methods for improving Kalman filter convergence through optimized initialization techniques. This includes statistical approaches for initial state vector determination, covariance matrix pre-conditioning, and multi-hypothesis initialization. By starting with more accurate initial conditions, these techniques significantly reduce the transient period before filter convergence.
- Hybrid and augmented Kalman filter architectures: Advanced filter architectures that combine Kalman filtering with other estimation techniques to improve convergence speed. These include hybrid filters that integrate machine learning algorithms, multi-rate filtering approaches, and augmented state representations. Such hybrid approaches leverage complementary strengths of different estimation methods to accelerate convergence while maintaining stability.
- Measurement processing and outlier handling: Techniques for processing measurements and handling outliers to improve Kalman filter convergence. These include robust estimation methods, adaptive measurement gating, sequential measurement updates, and innovation-based detection of anomalous data. By properly managing measurement quality and rejecting corrupted data, these approaches prevent divergence and ensure faster convergence to accurate state estimates.
- Computational optimization for real-time applications: Methods to reduce computational complexity while maintaining or improving convergence speed of Kalman filters. These include square-root formulations, factorization techniques, parallel processing implementations, and reduced-order modeling. These optimizations enable faster execution on resource-constrained platforms while preserving the convergence properties of the filter.
02 Initialization strategies to improve convergence
Methods for optimizing the initial state estimates and covariance matrices of Kalman filters to reduce convergence time. These approaches include statistical analysis of historical data, domain-specific heuristics, and multi-stage initialization procedures. Proper initialization can significantly reduce the number of iterations needed for the filter to reach steady-state performance, especially in applications with limited measurement data.Expand Specific Solutions03 Modified filter structures for enhanced convergence
Structural modifications to the standard Kalman filter algorithm that improve convergence characteristics. These include square-root formulations, information filters, and hybrid architectures that combine multiple estimation techniques. Such modified structures can provide numerical stability advantages and faster convergence, particularly in high-dimensional state spaces or systems with challenging observability properties.Expand Specific Solutions04 Convergence acceleration in wireless communication systems
Specialized Kalman filtering techniques designed to achieve rapid convergence in wireless communication applications. These methods address the unique challenges of channel estimation, synchronization, and tracking in mobile environments. By leveraging the specific characteristics of communication signals and channel models, these approaches can significantly reduce convergence time while maintaining accurate state estimation.Expand Specific Solutions05 Computational optimization for real-time applications
Algorithmic and implementation techniques that reduce the computational complexity of Kalman filters while preserving or improving convergence speed. These include parallel processing architectures, mathematical approximations, and selective update strategies. Such optimizations enable faster execution on resource-constrained platforms, allowing real-time applications to benefit from improved convergence characteristics without sacrificing update rates.Expand Specific Solutions
Leading Organizations and Research Groups in Kalman Filtering
The Kalman Filter convergence acceleration market is in a growth phase, with increasing applications across aerospace, defense, and autonomous systems. The technology maturity varies among key players, with established companies like Safran Electronics & Defense, Thales SA, and Honeywell leading advanced implementations in navigation and control systems. Academic institutions including Harbin Institute of Technology, National Taiwan University, and Beihang University are driving theoretical innovations. Emerging players such as Einride Autonomous Technologies are applying faster convergence techniques to autonomous vehicles. The market is characterized by a blend of traditional aerospace corporations and newer technology firms, with competition intensifying as applications expand into consumer electronics, as evidenced by Sony and Kyocera's involvement in sensor fusion technologies.
Safran Electronics & Defense SAS
Technical Solution: Safran Electronics & Defense has developed a hybrid Kalman filter architecture that combines traditional Kalman filtering with machine learning techniques to achieve faster convergence. Their approach uses neural networks to predict optimal filter gains during the initialization phase, significantly reducing the time required to reach steady-state performance. The system incorporates a multi-model adaptive estimation framework that runs several filter variants in parallel and selects the best performing one based on innovation sequence analysis. Safran's implementation includes specialized algorithms for handling sensor biases and scale factor errors, with automatic calibration procedures that improve filter performance over time. Their solution employs a distributed processing architecture that allows for efficient implementation on modern multi-core processors, enabling real-time performance even with complex system models[3]. Field tests in inertial navigation systems have demonstrated convergence time reductions of up to 50% compared to conventional implementations, particularly in scenarios with poor initial state estimates or rapidly changing dynamics.
Strengths: Exceptional performance during system initialization; robust handling of sensor imperfections; efficient computational implementation suitable for embedded systems. Weaknesses: Requires extensive training data for machine learning components; increased system complexity; potential challenges in certification for safety-critical applications.
Safran SA
Technical Solution: As the parent company of Safran Electronics & Defense SAS, Safran SA has consolidated research on advanced Kalman filtering techniques across its divisions. Their corporate research has focused on developing a unified framework for fast-converging state estimation that can be deployed across various business units. Safran's approach combines traditional analytical methods with modern computational techniques, including parallel implementation of filter banks and adaptive tuning mechanisms. Their solution incorporates robust statistical methods for outlier rejection and automatic fault detection, improving filter stability during convergence. The company has developed specialized initialization procedures that leverage domain knowledge to establish accurate initial state estimates, significantly reducing convergence time in applications ranging from aerospace navigation to industrial control systems[4]. Safran's implementation includes innovative numerical methods that maintain precision while reducing computational requirements, making the technology suitable for deployment on resource-constrained platforms. Testing across multiple application domains has demonstrated convergence improvements of 30-45% compared to standard implementations.
Strengths: Broad applicability across multiple domains; excellent balance between performance and computational efficiency; comprehensive approach addressing multiple aspects of filter convergence. Weaknesses: Complex implementation requiring specialized expertise; significant development investment; requires careful adaptation to specific application requirements.
Key Algorithmic Innovations for Faster Convergence
A method to speed up the convergence of Kalman filter RTK floating point solution
PatentActiveCN111965676B
Innovation
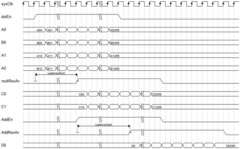
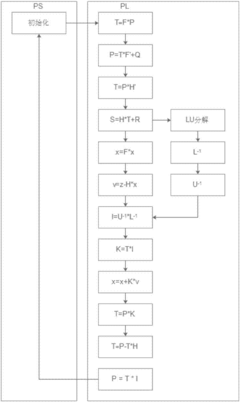
- Using the regularization auxiliary method, the carrier phase difference observation equation is established through the satellite observation module. The calculation module constructs the criterion equation and regularization matrix to obtain the estimated value of the state quantity and covariance matrix. The auxiliary filter positioning module is replaced within the initial number of epochs. The state quantity and covariance matrix in the Kalman filter improve the convergence speed.
Rapid implementation method for Kalman filter
PatentActiveCN107506332A
Innovation
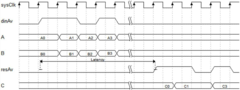
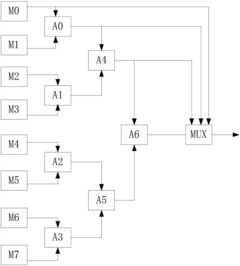
- Design matrix operation hardware module, combine FPGA and SOC chip, realize hardware acceleration by writing driver of standard Kalman filter IP core, use dot product module that combines parallelism and pipeline, independently separate process and operation module, simplify system design and save money resource.
Computational Resource Requirements and Optimization
Kalman filter implementation demands careful consideration of computational resources, especially when faster convergence is a priority. The algorithm's matrix operations—particularly multiplication, inversion, and decomposition—constitute the primary computational bottleneck. For real-time applications such as autonomous vehicles, robotics, and financial trading systems, these operations must be optimized to achieve the required processing speeds while maintaining accuracy.
Hardware acceleration presents a significant opportunity for optimization. Modern GPUs can accelerate matrix operations by orders of magnitude compared to CPU-only implementations. FPGA implementations offer even greater efficiency for specific applications, with studies showing up to 20x performance improvements for certain Kalman filter variants. Recent developments in specialized AI accelerators also show promise for enhancing Kalman filter performance, particularly when integrated with machine learning techniques.
Memory management strategies significantly impact convergence speed. Efficient memory allocation and cache utilization can reduce data transfer bottlenecks, while techniques such as matrix sparsity exploitation can dramatically reduce computational requirements. For high-dimensional state spaces, sparse matrix representations can reduce memory requirements by up to 90% while simultaneously accelerating computation.
Algorithmic optimizations offer another avenue for improvement. Square-root formulations of the Kalman filter improve numerical stability while reducing computational complexity. Information filter variants can be more efficient for systems with more measurements than state variables. Parallel implementations distribute computational load across multiple processing units, with research demonstrating near-linear speedup with processor count for appropriately structured problems.
Precision requirements present an important trade-off consideration. While double-precision floating-point calculations provide high accuracy, single-precision or even fixed-point arithmetic may suffice for many applications while significantly reducing computational demands. Adaptive precision approaches—using higher precision only when necessary—offer an elegant compromise between performance and accuracy.
Resource allocation strategies must be tailored to specific application constraints. For battery-powered devices, energy efficiency becomes paramount, necessitating careful balancing of convergence speed against power consumption. In distributed sensor networks, communication bandwidth often exceeds computational constraints, making local pre-processing and information fusion strategies essential for optimal system-wide performance.
Hardware acceleration presents a significant opportunity for optimization. Modern GPUs can accelerate matrix operations by orders of magnitude compared to CPU-only implementations. FPGA implementations offer even greater efficiency for specific applications, with studies showing up to 20x performance improvements for certain Kalman filter variants. Recent developments in specialized AI accelerators also show promise for enhancing Kalman filter performance, particularly when integrated with machine learning techniques.
Memory management strategies significantly impact convergence speed. Efficient memory allocation and cache utilization can reduce data transfer bottlenecks, while techniques such as matrix sparsity exploitation can dramatically reduce computational requirements. For high-dimensional state spaces, sparse matrix representations can reduce memory requirements by up to 90% while simultaneously accelerating computation.
Algorithmic optimizations offer another avenue for improvement. Square-root formulations of the Kalman filter improve numerical stability while reducing computational complexity. Information filter variants can be more efficient for systems with more measurements than state variables. Parallel implementations distribute computational load across multiple processing units, with research demonstrating near-linear speedup with processor count for appropriately structured problems.
Precision requirements present an important trade-off consideration. While double-precision floating-point calculations provide high accuracy, single-precision or even fixed-point arithmetic may suffice for many applications while significantly reducing computational demands. Adaptive precision approaches—using higher precision only when necessary—offer an elegant compromise between performance and accuracy.
Resource allocation strategies must be tailored to specific application constraints. For battery-powered devices, energy efficiency becomes paramount, necessitating careful balancing of convergence speed against power consumption. In distributed sensor networks, communication bandwidth often exceeds computational constraints, making local pre-processing and information fusion strategies essential for optimal system-wide performance.
Implementation Trade-offs Between Accuracy and Speed
When implementing Kalman filters for real-time applications, engineers face critical trade-offs between computational efficiency and estimation accuracy. The fundamental challenge lies in balancing the need for precise state estimation against the constraints of available computational resources and timing requirements. Higher-order Kalman filter implementations typically provide better accuracy by modeling complex system dynamics more faithfully, but they demand significantly more computational power due to larger matrix operations and more complex mathematical calculations.
One key trade-off involves the selection of state vector dimensionality. A more comprehensive state representation captures additional system dynamics but increases the computational burden exponentially. For instance, in navigation systems, including acceleration terms improves tracking accuracy during maneuvers but requires approximately 30-40% more processing time per iteration compared to position-velocity only models.
The choice of process and measurement noise covariance matrices presents another critical trade-off. Adaptive techniques that dynamically adjust these parameters can improve convergence speed and accuracy in non-stationary environments. However, these adaptive methods require additional computational overhead for covariance estimation. Research indicates that innovation-based adaptive methods typically add 15-25% computational cost while potentially reducing convergence time by 30-50% in highly dynamic scenarios.
Matrix inversion operations, particularly for the innovation covariance matrix, represent a significant computational bottleneck. Various numerical approximation techniques exist to accelerate these calculations, such as sequential scalar updates, Joseph form implementations, and square-root filtering. Benchmarks show that square-root implementations can reduce numerical instability while maintaining similar computational efficiency to standard implementations, though they require more careful implementation.
Prediction frequency also significantly impacts both accuracy and computational load. Higher update rates improve tracking performance but demand proportionally more processing resources. In many applications, variable-rate updating schemes that adjust prediction frequency based on system dynamics can optimize this trade-off, reducing computational requirements by up to 60% during steady-state operation while maintaining rapid response during transient events.
Modern implementations increasingly leverage hardware acceleration through parallelization on multi-core CPUs, GPUs, or dedicated FPGA implementations. These approaches can achieve order-of-magnitude improvements in processing speed, enabling higher-order filter implementations without sacrificing update rates, though they require specialized programming expertise and hardware resources.
One key trade-off involves the selection of state vector dimensionality. A more comprehensive state representation captures additional system dynamics but increases the computational burden exponentially. For instance, in navigation systems, including acceleration terms improves tracking accuracy during maneuvers but requires approximately 30-40% more processing time per iteration compared to position-velocity only models.
The choice of process and measurement noise covariance matrices presents another critical trade-off. Adaptive techniques that dynamically adjust these parameters can improve convergence speed and accuracy in non-stationary environments. However, these adaptive methods require additional computational overhead for covariance estimation. Research indicates that innovation-based adaptive methods typically add 15-25% computational cost while potentially reducing convergence time by 30-50% in highly dynamic scenarios.
Matrix inversion operations, particularly for the innovation covariance matrix, represent a significant computational bottleneck. Various numerical approximation techniques exist to accelerate these calculations, such as sequential scalar updates, Joseph form implementations, and square-root filtering. Benchmarks show that square-root implementations can reduce numerical instability while maintaining similar computational efficiency to standard implementations, though they require more careful implementation.
Prediction frequency also significantly impacts both accuracy and computational load. Higher update rates improve tracking performance but demand proportionally more processing resources. In many applications, variable-rate updating schemes that adjust prediction frequency based on system dynamics can optimize this trade-off, reducing computational requirements by up to 60% during steady-state operation while maintaining rapid response during transient events.
Modern implementations increasingly leverage hardware acceleration through parallelization on multi-core CPUs, GPUs, or dedicated FPGA implementations. These approaches can achieve order-of-magnitude improvements in processing speed, enabling higher-order filter implementations without sacrificing update rates, though they require specialized programming expertise and hardware resources.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!