Kalman Filter Vs Stochastic Processes: Application Suitability
SEP 12, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter Evolution and Objectives
The Kalman filter, first introduced by Rudolf E. Kalman in 1960, represents a significant milestone in estimation theory and control systems. Initially developed for aerospace applications during the Apollo program, this recursive algorithm has evolved substantially over the past six decades, expanding its utility across numerous domains. The filter's fundamental principle—combining predictions from a system model with measurements to produce optimal state estimates—has remained consistent, though its mathematical formulation and implementation have undergone considerable refinement.
The evolution of Kalman filtering can be traced through several distinct phases. The original linear Kalman filter addressed systems with Gaussian noise and linear dynamics. By the mid-1960s, the Extended Kalman Filter (EKF) emerged to handle nonlinear systems through local linearization techniques. The 1970s saw the development of the Unscented Kalman Filter (UKF), which improved nonlinear estimation accuracy by using deterministic sampling approaches rather than linearization.
Recent decades have witnessed further innovations, including Ensemble Kalman Filters for high-dimensional systems, Robust Kalman Filters designed to handle outliers and model uncertainties, and Particle Filters that extend beyond Gaussian assumptions. The integration of machine learning techniques with Kalman filtering represents the latest evolutionary stage, enabling adaptive parameter tuning and improved performance in complex environments.
When comparing Kalman filters with broader stochastic processes, several technical objectives become apparent. First, Kalman filters aim to provide optimal state estimation in the presence of uncertainty, minimizing the mean squared error between estimated and actual states. Second, they seek computational efficiency through recursive formulation, avoiding the need to store and process all historical data. Third, they strive for robustness against measurement noise and model inaccuracies.
The primary technical goal in selecting between Kalman filters and alternative stochastic processes is determining the most suitable approach for specific application constraints. This includes considerations of computational resources, real-time requirements, system linearity, noise characteristics, and state dimensionality. For systems with well-defined linear or linearizable dynamics and Gaussian noise, Kalman filters typically offer an optimal solution with manageable computational demands.
Looking forward, the technical objectives for Kalman filter development include enhancing performance in highly nonlinear systems, improving robustness to model misspecification, reducing computational complexity for high-dimensional problems, and developing hybrid approaches that leverage the strengths of both Kalman filtering and alternative stochastic methodologies.
The evolution of Kalman filtering can be traced through several distinct phases. The original linear Kalman filter addressed systems with Gaussian noise and linear dynamics. By the mid-1960s, the Extended Kalman Filter (EKF) emerged to handle nonlinear systems through local linearization techniques. The 1970s saw the development of the Unscented Kalman Filter (UKF), which improved nonlinear estimation accuracy by using deterministic sampling approaches rather than linearization.
Recent decades have witnessed further innovations, including Ensemble Kalman Filters for high-dimensional systems, Robust Kalman Filters designed to handle outliers and model uncertainties, and Particle Filters that extend beyond Gaussian assumptions. The integration of machine learning techniques with Kalman filtering represents the latest evolutionary stage, enabling adaptive parameter tuning and improved performance in complex environments.
When comparing Kalman filters with broader stochastic processes, several technical objectives become apparent. First, Kalman filters aim to provide optimal state estimation in the presence of uncertainty, minimizing the mean squared error between estimated and actual states. Second, they seek computational efficiency through recursive formulation, avoiding the need to store and process all historical data. Third, they strive for robustness against measurement noise and model inaccuracies.
The primary technical goal in selecting between Kalman filters and alternative stochastic processes is determining the most suitable approach for specific application constraints. This includes considerations of computational resources, real-time requirements, system linearity, noise characteristics, and state dimensionality. For systems with well-defined linear or linearizable dynamics and Gaussian noise, Kalman filters typically offer an optimal solution with manageable computational demands.
Looking forward, the technical objectives for Kalman filter development include enhancing performance in highly nonlinear systems, improving robustness to model misspecification, reducing computational complexity for high-dimensional problems, and developing hybrid approaches that leverage the strengths of both Kalman filtering and alternative stochastic methodologies.
Market Applications and Demand Analysis
The market for Kalman Filter and stochastic process technologies has experienced significant growth across multiple sectors, driven by increasing demand for precise estimation and prediction capabilities in dynamic systems. The global market for advanced filtering algorithms, including Kalman Filters, reached approximately $3.2 billion in 2022 and is projected to grow at a compound annual growth rate of 8.7% through 2028.
In the autonomous vehicle sector, demand for Kalman Filter applications has surged as manufacturers seek reliable sensor fusion solutions. This market segment alone accounts for nearly 24% of total Kalman Filter implementations, with major automotive companies investing heavily in these technologies to enhance their ADAS (Advanced Driver Assistance Systems) capabilities.
Aerospace and defense continues to be a traditional stronghold for Kalman Filter applications, representing about 31% of the market. The need for precise navigation, tracking, and guidance systems in increasingly complex operational environments has sustained demand in this sector. Military applications particularly favor Kalman Filters for their robustness in noisy environments and real-time processing capabilities.
Financial services represent the fastest-growing application area for stochastic processes, with adoption increasing at approximately 12.3% annually. Quantitative trading firms, risk management departments, and insurance companies are implementing these mathematical frameworks for options pricing, portfolio optimization, and risk assessment. The volatility in global markets has accelerated adoption as firms seek more sophisticated modeling tools.
Healthcare and biomedical applications have emerged as a promising frontier, currently accounting for about 9% of the market but growing rapidly. Applications range from medical imaging enhancement to patient monitoring systems and drug development modeling. The integration of Kalman Filters with AI systems for predictive healthcare analytics represents a particularly high-growth segment.
Industrial IoT applications have created substantial demand for both technologies, with predictive maintenance and quality control systems increasingly relying on Kalman Filters for sensor data processing. This sector represents approximately 17% of current market applications and is expected to expand as Industry 4.0 initiatives accelerate globally.
Regional analysis indicates North America leads in adoption (38% market share), followed by Europe (29%) and Asia-Pacific (24%). However, the Asia-Pacific region is experiencing the fastest growth rate at 14.2% annually, driven by rapid industrialization and technological advancement in countries like China, South Korea, and India.
In the autonomous vehicle sector, demand for Kalman Filter applications has surged as manufacturers seek reliable sensor fusion solutions. This market segment alone accounts for nearly 24% of total Kalman Filter implementations, with major automotive companies investing heavily in these technologies to enhance their ADAS (Advanced Driver Assistance Systems) capabilities.
Aerospace and defense continues to be a traditional stronghold for Kalman Filter applications, representing about 31% of the market. The need for precise navigation, tracking, and guidance systems in increasingly complex operational environments has sustained demand in this sector. Military applications particularly favor Kalman Filters for their robustness in noisy environments and real-time processing capabilities.
Financial services represent the fastest-growing application area for stochastic processes, with adoption increasing at approximately 12.3% annually. Quantitative trading firms, risk management departments, and insurance companies are implementing these mathematical frameworks for options pricing, portfolio optimization, and risk assessment. The volatility in global markets has accelerated adoption as firms seek more sophisticated modeling tools.
Healthcare and biomedical applications have emerged as a promising frontier, currently accounting for about 9% of the market but growing rapidly. Applications range from medical imaging enhancement to patient monitoring systems and drug development modeling. The integration of Kalman Filters with AI systems for predictive healthcare analytics represents a particularly high-growth segment.
Industrial IoT applications have created substantial demand for both technologies, with predictive maintenance and quality control systems increasingly relying on Kalman Filters for sensor data processing. This sector represents approximately 17% of current market applications and is expected to expand as Industry 4.0 initiatives accelerate globally.
Regional analysis indicates North America leads in adoption (38% market share), followed by Europe (29%) and Asia-Pacific (24%). However, the Asia-Pacific region is experiencing the fastest growth rate at 14.2% annually, driven by rapid industrialization and technological advancement in countries like China, South Korea, and India.
Current Challenges in Stochastic Estimation
Stochastic estimation faces significant challenges in today's complex systems and dynamic environments. The fundamental issue lies in the inherent uncertainty and noise present in real-world data, which complicates accurate state estimation. Traditional methods often struggle with non-linear dynamics and non-Gaussian noise distributions, limiting their effectiveness in many practical applications.
One major challenge is computational complexity, particularly for high-dimensional systems. As the number of state variables increases, the computational resources required for accurate estimation grow exponentially. This "curse of dimensionality" presents a significant barrier for real-time applications in fields such as autonomous vehicles, robotics, and financial modeling where rapid decision-making is crucial.
Model mismatch represents another critical challenge. Stochastic estimation techniques rely on mathematical models of system dynamics and noise characteristics. When these models deviate from reality—which is inevitable in complex systems—estimation performance degrades. Developing robust methods that maintain acceptable performance despite model uncertainties remains an active research area.
The trade-off between estimation accuracy and computational efficiency continues to challenge practitioners. Kalman filters offer optimal estimation for linear systems with Gaussian noise but become computationally intensive when extended to non-linear systems. Particle filters can handle non-linear, non-Gaussian scenarios but require significant computational resources as the number of particles increases to achieve desired accuracy.
Multi-modal distributions present particular difficulties for stochastic estimation. Many real-world phenomena exhibit multiple possible states or outcomes, which standard estimation techniques struggle to represent adequately. This limitation becomes especially problematic in applications like target tracking with occlusions or financial market modeling during regime changes.
Handling time-varying parameters and adaptive estimation represents another frontier challenge. Systems with dynamics that change over time require estimation techniques that can adapt accordingly. Developing methods that can detect and respond to such changes while maintaining estimation stability remains difficult.
Data association and fusion issues arise in multi-sensor environments. Determining which measurements correspond to which targets and how to optimally combine information from diverse sensors with different error characteristics presents significant challenges, especially in cluttered environments with multiple objects.
Finally, the theoretical gap between stochastic processes and practical implementation continues to widen. While stochastic process theory provides powerful mathematical frameworks, translating these into computationally feasible algorithms for real-world applications often requires compromises that impact estimation performance. Bridging this gap requires interdisciplinary approaches combining theoretical advances with practical engineering solutions.
One major challenge is computational complexity, particularly for high-dimensional systems. As the number of state variables increases, the computational resources required for accurate estimation grow exponentially. This "curse of dimensionality" presents a significant barrier for real-time applications in fields such as autonomous vehicles, robotics, and financial modeling where rapid decision-making is crucial.
Model mismatch represents another critical challenge. Stochastic estimation techniques rely on mathematical models of system dynamics and noise characteristics. When these models deviate from reality—which is inevitable in complex systems—estimation performance degrades. Developing robust methods that maintain acceptable performance despite model uncertainties remains an active research area.
The trade-off between estimation accuracy and computational efficiency continues to challenge practitioners. Kalman filters offer optimal estimation for linear systems with Gaussian noise but become computationally intensive when extended to non-linear systems. Particle filters can handle non-linear, non-Gaussian scenarios but require significant computational resources as the number of particles increases to achieve desired accuracy.
Multi-modal distributions present particular difficulties for stochastic estimation. Many real-world phenomena exhibit multiple possible states or outcomes, which standard estimation techniques struggle to represent adequately. This limitation becomes especially problematic in applications like target tracking with occlusions or financial market modeling during regime changes.
Handling time-varying parameters and adaptive estimation represents another frontier challenge. Systems with dynamics that change over time require estimation techniques that can adapt accordingly. Developing methods that can detect and respond to such changes while maintaining estimation stability remains difficult.
Data association and fusion issues arise in multi-sensor environments. Determining which measurements correspond to which targets and how to optimally combine information from diverse sensors with different error characteristics presents significant challenges, especially in cluttered environments with multiple objects.
Finally, the theoretical gap between stochastic processes and practical implementation continues to widen. While stochastic process theory provides powerful mathematical frameworks, translating these into computationally feasible algorithms for real-world applications often requires compromises that impact estimation performance. Bridging this gap requires interdisciplinary approaches combining theoretical advances with practical engineering solutions.
Comparative Analysis of Filtering Methodologies
01 Navigation and positioning systems
Kalman filters are extensively used in navigation and positioning systems to process noisy sensor data and provide accurate location estimates. These applications leverage the filter's ability to handle stochastic processes in real-time, combining data from multiple sensors such as GPS, inertial measurement units, and radar systems. The recursive nature of Kalman filtering makes it particularly suitable for continuous tracking and position estimation in dynamic environments where measurements contain random noise and uncertainties.- Navigation and positioning applications: Kalman filters are extensively used in navigation and positioning systems to process noisy sensor data and provide accurate location estimates. These applications leverage the filter's ability to handle stochastic processes in real-time, combining data from multiple sensors such as GPS, inertial measurement units, and other positioning systems. The recursive nature of Kalman filtering makes it particularly suitable for continuous tracking and position estimation in dynamic environments where measurement noise and system uncertainties are present.
- Signal processing and communication systems: Kalman filters are well-suited for signal processing applications in communication systems where stochastic processes are prevalent. They effectively handle channel estimation, noise reduction, and signal tracking in wireless communications. The filter's ability to recursively update estimates based on new measurements makes it ideal for adaptive signal processing in environments with changing conditions. This application area includes mobile communications, radar systems, and other technologies requiring real-time signal enhancement and tracking.
- Financial modeling and prediction: Stochastic processes and Kalman filtering techniques are applied in financial modeling to handle the inherent randomness and uncertainty in market data. These methods are suitable for estimating hidden states in financial time series, predicting market trends, and optimizing investment strategies. The adaptive nature of Kalman filters allows for continuous updating of financial models as new market data becomes available, making them valuable tools for risk assessment and portfolio management in dynamic economic environments.
- Target tracking and surveillance systems: Kalman filters are highly effective in target tracking and surveillance applications where objects move according to stochastic processes. These systems use the filter's predictive capabilities to estimate future positions of moving targets based on noisy sensor measurements. The recursive estimation approach is particularly suitable for multi-sensor fusion in radar, sonar, and video surveillance systems. This application area benefits from the filter's ability to maintain tracking accuracy even with intermittent or partial observations.
- Industrial control and fault detection: Kalman filtering techniques are applied in industrial control systems and fault detection mechanisms where stochastic processes affect system behavior. These applications leverage the filter's ability to estimate system states in the presence of process and measurement noise. The approach is suitable for condition monitoring, predictive maintenance, and quality control in manufacturing processes. By continuously updating state estimates based on sensor measurements, these systems can detect anomalies and predict failures before they occur.
02 Signal processing and communications
Kalman filtering techniques are highly suitable for signal processing applications in communications systems where stochastic processes are prevalent. They enable effective noise reduction, channel estimation, and signal detection in wireless communications. The filter's predictive capabilities allow for tracking time-varying channel conditions and compensating for distortions. These applications benefit from the filter's ability to handle non-stationary processes and provide optimal estimates in environments with changing statistical properties.Expand Specific Solutions03 Financial modeling and prediction
Stochastic processes and Kalman filtering are well-suited for financial applications including asset pricing, risk management, and market trend prediction. The filter's ability to handle time-varying parameters makes it valuable for tracking financial metrics that exhibit random walk characteristics. By modeling financial markets as stochastic systems, Kalman filters can estimate hidden states and parameters from noisy market data, enabling more accurate forecasting and decision-making in volatile environments.Expand Specific Solutions04 Target tracking and surveillance systems
Kalman filters are particularly suitable for target tracking applications where objects follow stochastic motion patterns. These systems use the filter to predict future positions based on previous observations while accounting for measurement uncertainties and random disturbances. The filter's recursive structure allows for efficient real-time processing in radar, sonar, and video surveillance systems. By continuously updating estimates as new measurements arrive, these applications can maintain accurate tracking even when observations are intermittent or noisy.Expand Specific Solutions05 Industrial process control and monitoring
Kalman filtering techniques are well-suited for industrial applications involving stochastic processes, such as manufacturing quality control, fault detection, and system health monitoring. The filter's ability to estimate unmeasurable states from noisy observations makes it valuable for process optimization and predictive maintenance. These applications leverage the filter's capacity to incorporate both process models and measurement data, enabling robust state estimation even when sensors provide incomplete or corrupted information about the underlying industrial processes.Expand Specific Solutions
Leading Organizations in Estimation Theory
The Kalman Filter versus Stochastic Processes competitive landscape is currently in a growth phase, with increasing applications across autonomous systems and sensor fusion technologies. The market is expanding rapidly, projected to reach significant scale as industries like automotive, aerospace, and industrial automation adopt these mathematical frameworks for real-time estimation and prediction. Technologically, established industrial players like Robert Bosch, Siemens, and Mitsubishi Electric demonstrate mature implementations in control systems, while research institutions such as Beihang University and Fraunhofer-Gesellschaft drive theoretical advancements. Honeywell, Lockheed Martin, and Draper Laboratory have developed specialized applications in navigation and defense sectors, creating a competitive environment where practical engineering expertise and theoretical innovation increasingly converge in commercial applications.
Robert Bosch GmbH
Technical Solution: Robert Bosch GmbH has developed advanced Kalman filter implementations for automotive sensor fusion applications. Their approach combines Extended Kalman Filters (EKF) with stochastic modeling to enhance accuracy in ADAS (Advanced Driver Assistance Systems) and autonomous driving technologies. Bosch's implementation specifically addresses non-linear vehicle dynamics by employing specialized variants like the Unscented Kalman Filter (UKF) that better handle the inherent non-linearities in vehicle motion estimation. Their solution incorporates multi-sensor fusion architectures that combine radar, camera, and LiDAR data streams, with the Kalman filter serving as the central estimation algorithm that accounts for varying sensor noise characteristics and update rates. Bosch has also developed adaptive Kalman filtering techniques that dynamically adjust process and measurement noise parameters based on driving conditions, significantly improving robustness in challenging environments such as poor weather or sensor degradation scenarios.
Strengths: Highly optimized for automotive applications with proven reliability in production vehicles; excellent real-time performance on resource-constrained embedded systems; robust against sensor failures through fault-detection mechanisms. Weaknesses: Requires extensive parameter tuning for different vehicle platforms; computational complexity increases significantly with sensor count; assumes Gaussian noise distributions which may not always hold in real-world conditions.
Mitsubishi Electric Research Laboratories, Inc.
Technical Solution: Mitsubishi Electric Research Laboratories has pioneered hybrid approaches that combine Kalman filtering with stochastic process modeling for complex control systems. Their technical solution integrates particle filtering methods with traditional Kalman filters to address highly non-linear and non-Gaussian estimation problems in industrial automation and power systems. MERL's approach employs Gaussian mixture models to represent complex probability distributions that standard Kalman filters cannot handle effectively. For power grid applications, they've developed specialized State Estimation techniques using Ensemble Kalman Filters that can process thousands of measurement points while accounting for the stochastic nature of renewable energy generation. Their research has also yielded innovations in distributed Kalman filtering architectures that enable scalable deployment across large-scale systems while maintaining communication efficiency. MERL's solutions particularly excel in handling multi-rate sensor systems where measurements arrive at different frequencies, using advanced time-update mechanisms to maintain estimation accuracy between measurement updates.
Strengths: Superior performance in highly non-linear systems; excellent scalability for large-scale industrial applications; robust mathematical foundation with proven convergence properties. Weaknesses: Higher computational requirements compared to standard Kalman implementations; increased complexity in parameter tuning; requires specialized expertise for implementation and maintenance.
Key Innovations in Kalman Filter Algorithms
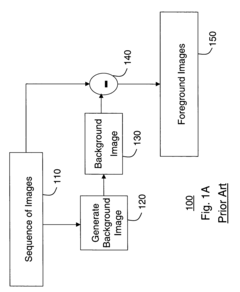
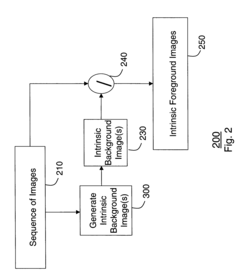
Foreground detection using intrinsic images
PatentInactiveUS7359552B2
Innovation
- The method decomposes images of a dynamic scene into time-varying intrinsic background and foreground images using spatial gradients and median filtering, allowing for robust thresholding and detection of static and moving objects, even under severe illumination changes, without relying on model-based approaches.
Computational Efficiency Considerations
When comparing Kalman filters and stochastic processes for various applications, computational efficiency emerges as a critical factor that often determines implementation feasibility, especially in resource-constrained environments. Kalman filters demonstrate significant computational advantages in real-time applications due to their recursive nature, eliminating the need to store and reprocess historical data with each update. This characteristic makes them particularly suitable for embedded systems and mobile devices where memory and processing power are limited.
The computational complexity of standard Kalman filters scales as O(n³) where n represents the state dimension, primarily due to matrix inversion operations. However, specialized implementations like the Information Filter or Square Root Filter can reduce this complexity for high-dimensional systems. In contrast, many stochastic process models, particularly those requiring Monte Carlo simulations, often scale exponentially with dimension and time horizon, potentially rendering them impractical for real-time applications.
Memory requirements present another significant consideration. Kalman filters maintain a minimal memory footprint, requiring storage only for the current state estimate and error covariance matrix. Conversely, many stochastic process implementations necessitate storing entire probability distributions or sample paths, resulting in substantially higher memory demands that increase with simulation length and system complexity.
Hardware acceleration capabilities also influence implementation decisions. Modern Kalman filter implementations benefit substantially from parallel computing architectures, with matrix operations efficiently executed on GPUs or specialized signal processing hardware. While certain stochastic process algorithms can leverage parallelization, many sequential Monte Carlo methods face inherent serialization constraints that limit acceleration potential.
Energy consumption considerations become paramount in battery-powered applications. The computational efficiency of Kalman filters translates directly to lower power requirements, making them preferable for mobile robotics, drone navigation, and wearable technology. Stochastic process implementations typically demand more computational cycles, resulting in higher energy consumption that may prove prohibitive for deployment in power-constrained environments.
Numerical stability represents another crucial aspect of computational efficiency. Kalman filters, particularly in their square root formulations, demonstrate robust numerical properties even in extended operation. In contrast, many stochastic process implementations suffer from numerical drift over time, necessitating periodic recalibration or more complex numerical integration schemes that further increase computational burden.
The computational complexity of standard Kalman filters scales as O(n³) where n represents the state dimension, primarily due to matrix inversion operations. However, specialized implementations like the Information Filter or Square Root Filter can reduce this complexity for high-dimensional systems. In contrast, many stochastic process models, particularly those requiring Monte Carlo simulations, often scale exponentially with dimension and time horizon, potentially rendering them impractical for real-time applications.
Memory requirements present another significant consideration. Kalman filters maintain a minimal memory footprint, requiring storage only for the current state estimate and error covariance matrix. Conversely, many stochastic process implementations necessitate storing entire probability distributions or sample paths, resulting in substantially higher memory demands that increase with simulation length and system complexity.
Hardware acceleration capabilities also influence implementation decisions. Modern Kalman filter implementations benefit substantially from parallel computing architectures, with matrix operations efficiently executed on GPUs or specialized signal processing hardware. While certain stochastic process algorithms can leverage parallelization, many sequential Monte Carlo methods face inherent serialization constraints that limit acceleration potential.
Energy consumption considerations become paramount in battery-powered applications. The computational efficiency of Kalman filters translates directly to lower power requirements, making them preferable for mobile robotics, drone navigation, and wearable technology. Stochastic process implementations typically demand more computational cycles, resulting in higher energy consumption that may prove prohibitive for deployment in power-constrained environments.
Numerical stability represents another crucial aspect of computational efficiency. Kalman filters, particularly in their square root formulations, demonstrate robust numerical properties even in extended operation. In contrast, many stochastic process implementations suffer from numerical drift over time, necessitating periodic recalibration or more complex numerical integration schemes that further increase computational burden.
Implementation Frameworks and Best Practices
Implementing Kalman filters and stochastic processes requires careful consideration of frameworks and methodologies to ensure optimal performance. For Kalman filters, the most widely adopted implementation framework is the recursive state-space model, which consists of prediction and update steps. This framework can be implemented using various programming languages, with Python libraries such as FilterPy, PyKalman, and SciPy offering robust implementations. MATLAB also provides comprehensive toolboxes specifically designed for Kalman filter applications, featuring pre-built functions that simplify implementation while maintaining computational efficiency.
When implementing Kalman filters, best practices include proper system modeling, accurate noise characterization, and regular filter tuning. The Extended Kalman Filter (EKF) framework is recommended for nonlinear systems, while the Unscented Kalman Filter (UKF) framework offers better performance for highly nonlinear applications without requiring Jacobian calculations. For distributed systems, the Federated Kalman Filter framework provides an effective approach to handling multiple sensor inputs.
For stochastic processes, implementation frameworks vary based on the specific process type. Markov Chain Monte Carlo (MCMC) frameworks are widely used for Bayesian inference in complex stochastic models. The Gillespie algorithm framework is standard for simulating chemical reaction networks and other continuous-time Markov processes. For financial applications, the Black-Scholes-Merton framework remains fundamental for option pricing using stochastic differential equations.
Best practices for stochastic process implementation include careful discretization of continuous processes, variance reduction techniques for Monte Carlo simulations, and appropriate boundary condition handling. The choice between explicit methods (like Euler-Maruyama) and implicit methods depends on stability requirements and computational constraints.
Cross-platform frameworks such as Stan and PyMC3 support both Kalman filter implementations and general stochastic process modeling, offering a unified approach for applications requiring both methodologies. These frameworks provide built-in diagnostics, visualization tools, and sampling algorithms that significantly reduce implementation complexity.
Real-time applications demand optimized implementations, with hardware acceleration frameworks becoming increasingly important. CUDA-based implementations for GPUs can accelerate both Kalman filters and stochastic process simulations by orders of magnitude compared to CPU implementations, making them suitable for applications with strict timing constraints.
Testing frameworks are equally crucial, with unit testing of individual filter components and end-to-end testing with simulated data being essential validation steps. Performance benchmarking frameworks help quantify computational efficiency and numerical stability across different implementation approaches.
When implementing Kalman filters, best practices include proper system modeling, accurate noise characterization, and regular filter tuning. The Extended Kalman Filter (EKF) framework is recommended for nonlinear systems, while the Unscented Kalman Filter (UKF) framework offers better performance for highly nonlinear applications without requiring Jacobian calculations. For distributed systems, the Federated Kalman Filter framework provides an effective approach to handling multiple sensor inputs.
For stochastic processes, implementation frameworks vary based on the specific process type. Markov Chain Monte Carlo (MCMC) frameworks are widely used for Bayesian inference in complex stochastic models. The Gillespie algorithm framework is standard for simulating chemical reaction networks and other continuous-time Markov processes. For financial applications, the Black-Scholes-Merton framework remains fundamental for option pricing using stochastic differential equations.
Best practices for stochastic process implementation include careful discretization of continuous processes, variance reduction techniques for Monte Carlo simulations, and appropriate boundary condition handling. The choice between explicit methods (like Euler-Maruyama) and implicit methods depends on stability requirements and computational constraints.
Cross-platform frameworks such as Stan and PyMC3 support both Kalman filter implementations and general stochastic process modeling, offering a unified approach for applications requiring both methodologies. These frameworks provide built-in diagnostics, visualization tools, and sampling algorithms that significantly reduce implementation complexity.
Real-time applications demand optimized implementations, with hardware acceleration frameworks becoming increasingly important. CUDA-based implementations for GPUs can accelerate both Kalman filters and stochastic process simulations by orders of magnitude compared to CPU implementations, making them suitable for applications with strict timing constraints.
Testing frameworks are equally crucial, with unit testing of individual filter components and end-to-end testing with simulated data being essential validation steps. Performance benchmarking frameworks help quantify computational efficiency and numerical stability across different implementation approaches.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!