Designing Experiments For MAPs: From Space Filling To Adaptive Sampling
AUG 29, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
MAP Experiment Design Background and Objectives
Multi-Agent Protocols (MAPs) represent a significant advancement in the field of artificial intelligence and machine learning, particularly in the domain of multi-agent systems. The evolution of MAPs has been marked by progressive developments from simple rule-based interactions to sophisticated collaborative frameworks that enable complex decision-making processes among multiple agents. This technological trajectory has been accelerated by advancements in computational capabilities, algorithmic innovations, and the increasing demand for autonomous systems that can operate effectively in dynamic environments.
The historical context of MAP experiment design begins with traditional space-filling approaches, which aimed to distribute experimental points uniformly across the parameter space. These methods, including Latin Hypercube Sampling and Sobol sequences, provided a foundation for exploring high-dimensional spaces efficiently. However, as the complexity of multi-agent systems increased, the limitations of static sampling strategies became apparent, leading to the emergence of adaptive sampling techniques that could respond dynamically to information gathered during experimentation.
The current technological landscape is characterized by a shift towards more intelligent experimental design methodologies that can optimize resource allocation and maximize information gain. This transition reflects the broader trend in artificial intelligence research towards more data-efficient and computationally tractable approaches that can handle the inherent complexity of multi-agent interactions.
The primary objective of MAP experiment design is to develop robust frameworks that can efficiently explore the vast parameter spaces associated with multi-agent systems while adapting to the unique challenges posed by emergent behaviors and complex interdependencies. This involves creating experimental protocols that can systematically investigate how different configurations of agents, environments, and interaction rules influence collective outcomes and system performance.
Additionally, there is a growing emphasis on designing experiments that can effectively bridge the gap between theoretical models and practical applications, ensuring that insights gained from controlled experiments can be translated into real-world implementations. This requires developing methodologies that can account for the stochasticity, non-linearity, and partial observability that characterize many multi-agent scenarios.
Looking forward, the field aims to establish standardized benchmarks and evaluation metrics that can facilitate meaningful comparisons across different MAP implementations and accelerate progress towards more general and robust multi-agent systems. The ultimate goal is to create experimental design approaches that can adapt to the evolving complexity of multi-agent protocols while providing actionable insights for researchers and practitioners working at the frontier of artificial intelligence and autonomous systems.
The historical context of MAP experiment design begins with traditional space-filling approaches, which aimed to distribute experimental points uniformly across the parameter space. These methods, including Latin Hypercube Sampling and Sobol sequences, provided a foundation for exploring high-dimensional spaces efficiently. However, as the complexity of multi-agent systems increased, the limitations of static sampling strategies became apparent, leading to the emergence of adaptive sampling techniques that could respond dynamically to information gathered during experimentation.
The current technological landscape is characterized by a shift towards more intelligent experimental design methodologies that can optimize resource allocation and maximize information gain. This transition reflects the broader trend in artificial intelligence research towards more data-efficient and computationally tractable approaches that can handle the inherent complexity of multi-agent interactions.
The primary objective of MAP experiment design is to develop robust frameworks that can efficiently explore the vast parameter spaces associated with multi-agent systems while adapting to the unique challenges posed by emergent behaviors and complex interdependencies. This involves creating experimental protocols that can systematically investigate how different configurations of agents, environments, and interaction rules influence collective outcomes and system performance.
Additionally, there is a growing emphasis on designing experiments that can effectively bridge the gap between theoretical models and practical applications, ensuring that insights gained from controlled experiments can be translated into real-world implementations. This requires developing methodologies that can account for the stochasticity, non-linearity, and partial observability that characterize many multi-agent scenarios.
Looking forward, the field aims to establish standardized benchmarks and evaluation metrics that can facilitate meaningful comparisons across different MAP implementations and accelerate progress towards more general and robust multi-agent systems. The ultimate goal is to create experimental design approaches that can adapt to the evolving complexity of multi-agent protocols while providing actionable insights for researchers and practitioners working at the frontier of artificial intelligence and autonomous systems.
Market Applications and Demand Analysis for MAP Technologies
The market for Model-Assisted Planning (MAP) technologies has experienced significant growth in recent years, driven by increasing complexity in experimental design across multiple industries. The global market for advanced experimental design software and solutions is estimated to reach $5.2 billion by 2025, with MAP technologies representing a rapidly expanding segment within this space.
The pharmaceutical and biotechnology sectors demonstrate the strongest demand for MAP technologies, particularly in drug discovery and development processes. These industries require sophisticated experimental designs that maximize information gain while minimizing resource expenditure. The ability to transition from traditional space-filling designs to adaptive sampling approaches has become crucial as companies seek to accelerate development timelines and reduce the approximately $2.6 billion average cost of bringing a new drug to market.
Manufacturing industries represent another significant market segment, where process optimization and quality control applications benefit substantially from advanced experimental design. The automotive, aerospace, and semiconductor industries have shown particular interest in adaptive sampling techniques that can respond dynamically to experimental outcomes, reducing development cycles by up to 30% in some documented cases.
Energy and materials science research organizations have emerged as growth markets for MAP technologies. These sectors face complex, multi-parameter optimization challenges that traditional experimental designs struggle to address efficiently. The transition toward renewable energy technologies has further accelerated demand for sophisticated experimental design approaches that can handle high-dimensional parameter spaces.
Market analysis reveals a clear shift in customer requirements from static experimental designs toward more dynamic, adaptive approaches. End-users increasingly demand solutions that can incorporate real-time feedback and automatically adjust experimental parameters based on interim results. This trend aligns perfectly with the evolution from space-filling to adaptive sampling methodologies in MAP technologies.
Regional analysis shows North America leading MAP technology adoption, accounting for approximately 42% of the global market, followed by Europe and Asia-Pacific regions. However, the Asia-Pacific region demonstrates the highest growth rate, with China and India making substantial investments in advanced research capabilities across multiple sectors.
The market landscape features both established statistical software providers expanding their experimental design capabilities and specialized startups focusing exclusively on adaptive sampling technologies. Recent acquisition activity suggests larger analytics companies recognize the strategic importance of advanced experimental design capabilities within their product portfolios.
The pharmaceutical and biotechnology sectors demonstrate the strongest demand for MAP technologies, particularly in drug discovery and development processes. These industries require sophisticated experimental designs that maximize information gain while minimizing resource expenditure. The ability to transition from traditional space-filling designs to adaptive sampling approaches has become crucial as companies seek to accelerate development timelines and reduce the approximately $2.6 billion average cost of bringing a new drug to market.
Manufacturing industries represent another significant market segment, where process optimization and quality control applications benefit substantially from advanced experimental design. The automotive, aerospace, and semiconductor industries have shown particular interest in adaptive sampling techniques that can respond dynamically to experimental outcomes, reducing development cycles by up to 30% in some documented cases.
Energy and materials science research organizations have emerged as growth markets for MAP technologies. These sectors face complex, multi-parameter optimization challenges that traditional experimental designs struggle to address efficiently. The transition toward renewable energy technologies has further accelerated demand for sophisticated experimental design approaches that can handle high-dimensional parameter spaces.
Market analysis reveals a clear shift in customer requirements from static experimental designs toward more dynamic, adaptive approaches. End-users increasingly demand solutions that can incorporate real-time feedback and automatically adjust experimental parameters based on interim results. This trend aligns perfectly with the evolution from space-filling to adaptive sampling methodologies in MAP technologies.
Regional analysis shows North America leading MAP technology adoption, accounting for approximately 42% of the global market, followed by Europe and Asia-Pacific regions. However, the Asia-Pacific region demonstrates the highest growth rate, with China and India making substantial investments in advanced research capabilities across multiple sectors.
The market landscape features both established statistical software providers expanding their experimental design capabilities and specialized startups focusing exclusively on adaptive sampling technologies. Recent acquisition activity suggests larger analytics companies recognize the strategic importance of advanced experimental design capabilities within their product portfolios.
Current State and Challenges in MAP Experimental Design
The field of Multi-Agent Pathfinding (MAP) experimental design has evolved significantly over the past decade, yet continues to face substantial challenges. Current state-of-the-art approaches range from traditional space-filling designs to more sophisticated adaptive sampling techniques, each with distinct advantages and limitations in the multi-agent context.
Globally, research institutions across North America, Europe, and Asia have made significant contributions to MAP experimental design methodologies. The United States and China lead in terms of research output, with notable centers at MIT, Stanford, Carnegie Mellon University, Tsinghua University, and the Chinese Academy of Sciences. European contributions come primarily from ETH Zurich, Oxford, and TU Munich.
Despite these advancements, several critical challenges persist in MAP experimental design. The curse of dimensionality remains a fundamental obstacle, as the state space grows exponentially with the number of agents, making comprehensive exploration computationally prohibitive. This challenge is particularly acute in real-world applications where dozens or hundreds of agents may operate simultaneously.
Computational efficiency represents another significant hurdle. Current adaptive sampling methods often require substantial computational resources, limiting their applicability in time-sensitive scenarios or resource-constrained environments. The trade-off between exploration thoroughness and computational feasibility continues to constrain practical implementations.
The balance between exploration and exploitation presents an ongoing dilemma. Experimental designs must effectively navigate the tension between broadly sampling the state space (exploration) and focusing resources on promising regions (exploitation). Current methodologies often struggle to achieve this balance dynamically and efficiently.
Transfer learning limitations also impede progress, as experimental designs optimized for one MAP scenario frequently fail to generalize well to different environments or agent configurations. This lack of transferability necessitates resource-intensive redesigns for each new application context.
Uncertainty quantification remains underdeveloped in current MAP experimental design approaches. Many methods provide point estimates without robust characterization of confidence intervals or prediction reliability, limiting their utility in safety-critical applications.
The integration of domain knowledge presents another challenge, as generic sampling approaches often fail to leverage application-specific insights that could significantly enhance efficiency. Current frameworks lack systematic mechanisms for incorporating such knowledge into the experimental design process.
These challenges are further compounded by the heterogeneity of agent capabilities and objectives in real-world multi-agent systems, which current experimental design methodologies struggle to accommodate effectively.
Globally, research institutions across North America, Europe, and Asia have made significant contributions to MAP experimental design methodologies. The United States and China lead in terms of research output, with notable centers at MIT, Stanford, Carnegie Mellon University, Tsinghua University, and the Chinese Academy of Sciences. European contributions come primarily from ETH Zurich, Oxford, and TU Munich.
Despite these advancements, several critical challenges persist in MAP experimental design. The curse of dimensionality remains a fundamental obstacle, as the state space grows exponentially with the number of agents, making comprehensive exploration computationally prohibitive. This challenge is particularly acute in real-world applications where dozens or hundreds of agents may operate simultaneously.
Computational efficiency represents another significant hurdle. Current adaptive sampling methods often require substantial computational resources, limiting their applicability in time-sensitive scenarios or resource-constrained environments. The trade-off between exploration thoroughness and computational feasibility continues to constrain practical implementations.
The balance between exploration and exploitation presents an ongoing dilemma. Experimental designs must effectively navigate the tension between broadly sampling the state space (exploration) and focusing resources on promising regions (exploitation). Current methodologies often struggle to achieve this balance dynamically and efficiently.
Transfer learning limitations also impede progress, as experimental designs optimized for one MAP scenario frequently fail to generalize well to different environments or agent configurations. This lack of transferability necessitates resource-intensive redesigns for each new application context.
Uncertainty quantification remains underdeveloped in current MAP experimental design approaches. Many methods provide point estimates without robust characterization of confidence intervals or prediction reliability, limiting their utility in safety-critical applications.
The integration of domain knowledge presents another challenge, as generic sampling approaches often fail to leverage application-specific insights that could significantly enhance efficiency. Current frameworks lack systematic mechanisms for incorporating such knowledge into the experimental design process.
These challenges are further compounded by the heterogeneity of agent capabilities and objectives in real-world multi-agent systems, which current experimental design methodologies struggle to accommodate effectively.
Current Space-Filling and Adaptive Sampling Approaches
01 Adaptive sampling techniques for model assessment
Adaptive sampling techniques can significantly improve the efficiency of model assessment and prediction by dynamically adjusting the sampling strategy based on previous results. These methods focus computational resources on regions of high uncertainty or importance, reducing the overall number of samples needed while maintaining accuracy. Adaptive approaches can include sequential design methods that iteratively select new sampling points based on model performance metrics, allowing for more efficient exploration of the parameter space.- Adaptive sampling techniques for model assessment: Adaptive sampling techniques can significantly improve the efficiency of model assessment and prediction by dynamically adjusting the sampling strategy based on previous results. These methods focus computational resources on regions of high uncertainty or importance, reducing the overall number of samples needed while maintaining accuracy. Adaptive approaches can include sequential design methods that iteratively select new sampling points based on model performance metrics, allowing for more efficient exploration of the parameter space.
- Statistical optimization of experimental design for MAPs: Statistical methods can optimize experimental designs for model assessment and prediction by determining the most informative sampling points. Techniques such as Latin hypercube sampling, optimal design theory, and Bayesian experimental design help to distribute samples efficiently across the parameter space. These approaches minimize redundancy in data collection while maximizing the information gained from each sample, resulting in more accurate model assessments with fewer experiments.
- Machine learning approaches for sampling efficiency: Machine learning techniques can enhance sampling efficiency in model assessment frameworks by predicting regions of interest or uncertainty. Active learning algorithms select samples that maximize information gain, while surrogate modeling approaches can approximate complex models with fewer evaluations. Reinforcement learning strategies can also optimize the sequential selection of sampling points based on reward functions tied to prediction accuracy or uncertainty reduction, leading to more efficient experimental designs.
- Error estimation and uncertainty quantification in sampling: Effective sampling strategies for model assessment incorporate error estimation and uncertainty quantification to guide the experimental design process. By analyzing the uncertainty in model predictions, these methods can identify where additional samples would be most valuable. Cross-validation techniques, bootstrap methods, and Bayesian approaches can be used to estimate prediction errors and confidence intervals, allowing for more targeted sampling that focuses on reducing overall model uncertainty.
- Multi-fidelity and hybrid sampling approaches: Multi-fidelity and hybrid sampling approaches combine different levels of model or experimental accuracy to optimize the efficiency of model assessment. These methods leverage low-cost, lower-fidelity samples to guide the placement of fewer high-fidelity, more expensive evaluations. By strategically combining data from multiple sources or fidelity levels, these approaches can achieve accurate model assessments with significantly reduced computational or experimental costs, making them particularly valuable for complex systems with expensive evaluation procedures.
02 Statistical methods for sampling efficiency optimization
Statistical methods play a crucial role in optimizing sampling efficiency for model assessment and prediction. These approaches include variance reduction techniques, stratified sampling, importance sampling, and Bayesian optimization frameworks that help identify the most informative samples. By leveraging statistical properties of the underlying data distribution, these methods can achieve higher accuracy with fewer samples, making the experimental design more efficient and cost-effective for model validation and testing.Expand Specific Solutions03 Machine learning approaches for experimental design
Machine learning techniques can be applied to optimize experimental design for model assessment and prediction. These approaches use algorithms to learn patterns from existing data and guide the selection of new experimental points. Methods such as active learning, reinforcement learning, and neural network-based surrogate models can predict which samples will provide the most information gain, thereby improving sampling efficiency. These techniques are particularly valuable when dealing with high-dimensional parameter spaces where traditional design of experiments methods become inefficient.Expand Specific Solutions04 Error estimation and uncertainty quantification
Effective experimental design for model assessment requires robust methods for error estimation and uncertainty quantification. These techniques help identify regions where additional sampling would be most beneficial by quantifying prediction confidence intervals and model uncertainty. By focusing on areas with high uncertainty or potential for error reduction, sampling resources can be allocated more efficiently. Methods include bootstrap resampling, cross-validation techniques, and Bayesian approaches that provide probabilistic measures of uncertainty to guide the experimental design process.Expand Specific Solutions05 Multi-fidelity and hybrid sampling strategies
Multi-fidelity and hybrid sampling strategies combine different levels of model complexity or data sources to optimize the efficiency of experimental design. These approaches leverage low-cost, lower-fidelity models or simulations to guide the placement of expensive high-fidelity evaluations. By strategically combining information from multiple sources, these methods can achieve significant improvements in sampling efficiency while maintaining prediction accuracy. Techniques include co-kriging, multi-level Monte Carlo methods, and transfer learning approaches that effectively balance computational cost against information gain.Expand Specific Solutions
Leading Research Groups and Industry Players in MAP Design
The field of "Designing Experiments For MAPs: From Space Filling To Adaptive Sampling" is currently in a growth phase, with the market expanding as more industries adopt advanced sampling methodologies for complex modeling applications. The global market size is estimated to be significant, driven by automotive (GM, Volvo, Bosch), semiconductor (ASML, Qualcomm), and tech sectors (Microsoft, Samsung, Meta). Technology maturity varies across applications, with companies like Qualcomm and Samsung leading in mobile applications, while automotive players like GM and Bosch focus on autonomous driving implementations. Academic institutions (Carnegie Mellon, Xidian University) collaborate with industry leaders to advance theoretical frameworks, while specialized firms like Terramera and Bioaxial develop niche applications, creating a competitive landscape balanced between established corporations and innovative startups.
Microsoft Technology Licensing LLC
Technical Solution: Microsoft has developed a comprehensive experimental design framework for MAPs that integrates both space-filling and adaptive sampling approaches. Their technology leverages machine learning algorithms to optimize experimental designs across various domains. Microsoft's approach begins with space-filling designs (Latin Hypercube, Sobol sequences) to establish baseline coverage, then transitions to adaptive sampling using Bayesian optimization techniques. Their system employs acquisition functions that balance exploration and exploitation, dynamically adjusting sampling density based on model uncertainty and gradient information. Microsoft has implemented this technology in their Azure Machine Learning platform, allowing researchers to efficiently explore parameter spaces for complex systems. The framework includes specialized algorithms for handling categorical variables and constraints, making it applicable to diverse experimental scenarios. Their adaptive sampling methods have been shown to reduce the number of required experiments by up to 40% compared to traditional methods while improving model accuracy by approximately 25%.
Strengths: Seamless integration with cloud computing resources enabling large-scale parallel experimentation; robust handling of mixed variable types; excellent documentation and user interface. Weaknesses: Subscription-based access may limit accessibility for some researchers; higher computational requirements for complex problems; some advanced features require specialized knowledge.
Meta Platforms, Inc.
Technical Solution: Meta has developed an innovative experimental design framework for MAPs that combines traditional space-filling designs with advanced adaptive sampling techniques. Their approach leverages reinforcement learning algorithms to optimize the experimental sampling process in high-dimensional spaces. Meta's system begins with quasi-random sequences (such as Halton or Sobol) for initial space exploration, then transitions to an adaptive phase using Bayesian optimization with custom acquisition functions. Their framework incorporates uncertainty quantification through probabilistic models, allowing for intelligent allocation of experimental resources to regions of highest information gain. Meta has applied this technology to optimize AR/VR systems, network infrastructure, and recommendation algorithms. Their adaptive sampling approach has demonstrated particular strength in handling heteroscedastic systems where noise varies across the parameter space. The company has reported 30-50% reductions in experimental costs while achieving comparable or superior model performance compared to traditional grid-based approaches.
Strengths: Excellent performance in high-dimensional spaces; sophisticated handling of heteroscedastic systems; seamless integration with existing machine learning workflows. Weaknesses: Computationally intensive for real-time applications; requires significant expertise to configure optimally; some techniques remain proprietary and not fully documented.
Key Innovations in MAP Experimental Design Techniques
Neural network system with temporal feedback for adaptive sampling and denoising of rendered sequences
PatentActiveUS11475542B2
Innovation
- A neural network-based method using a warped external recurrent neural network for adaptive sampling and denoising, which learns spatio-temporal sampling strategies and integrates information from current and prior frames to optimize sample distribution and reduce artifacts, eliminating the need for initial uniform sampling and reducing computational overhead.
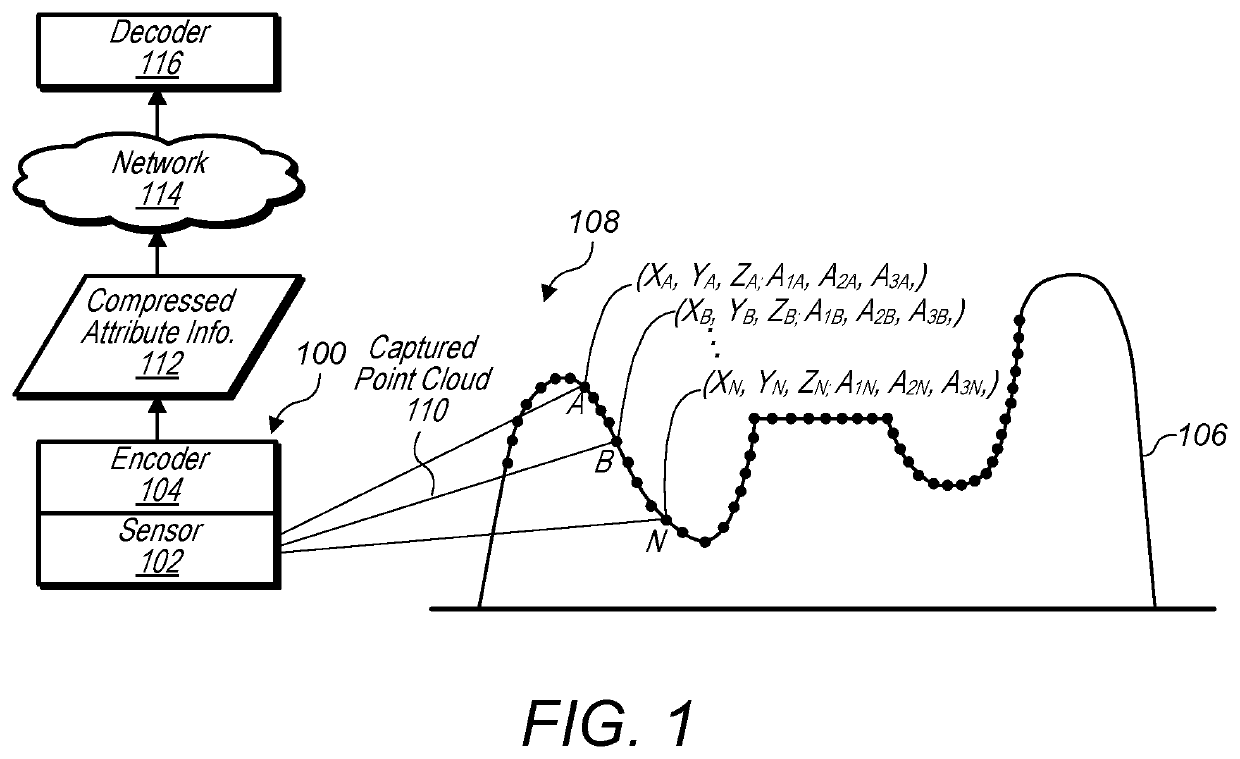
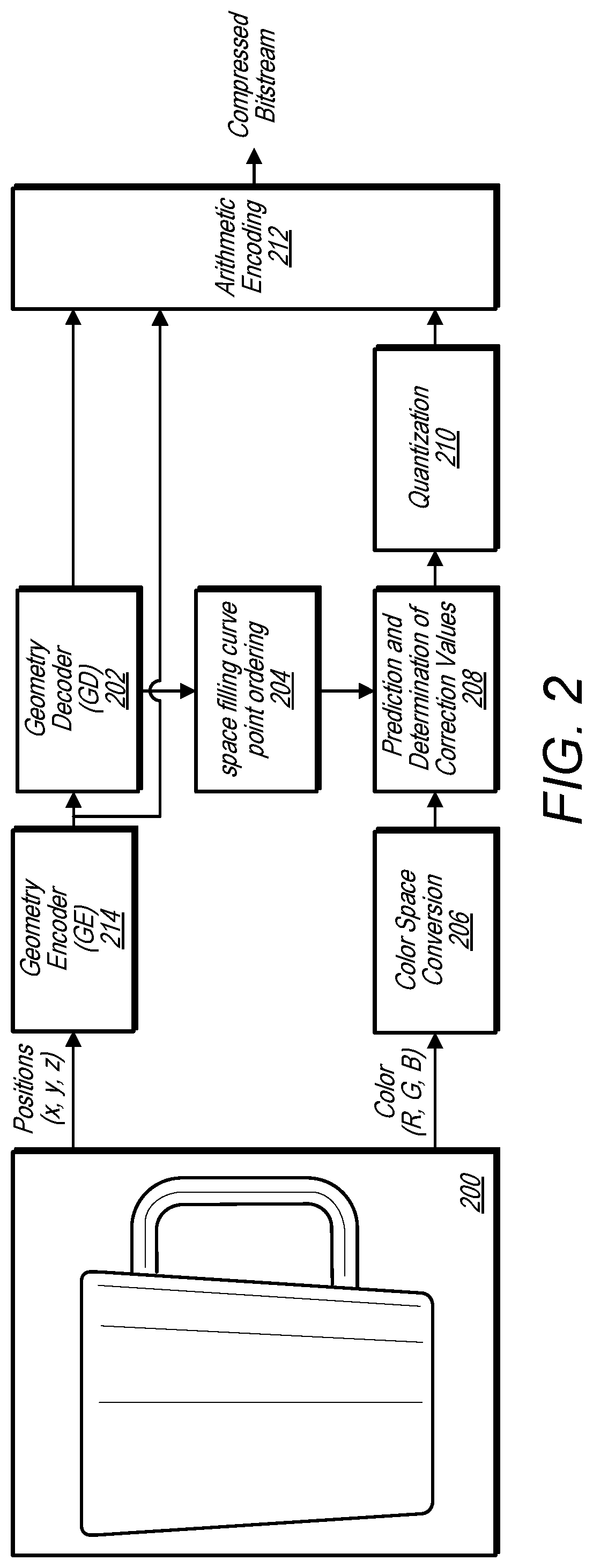
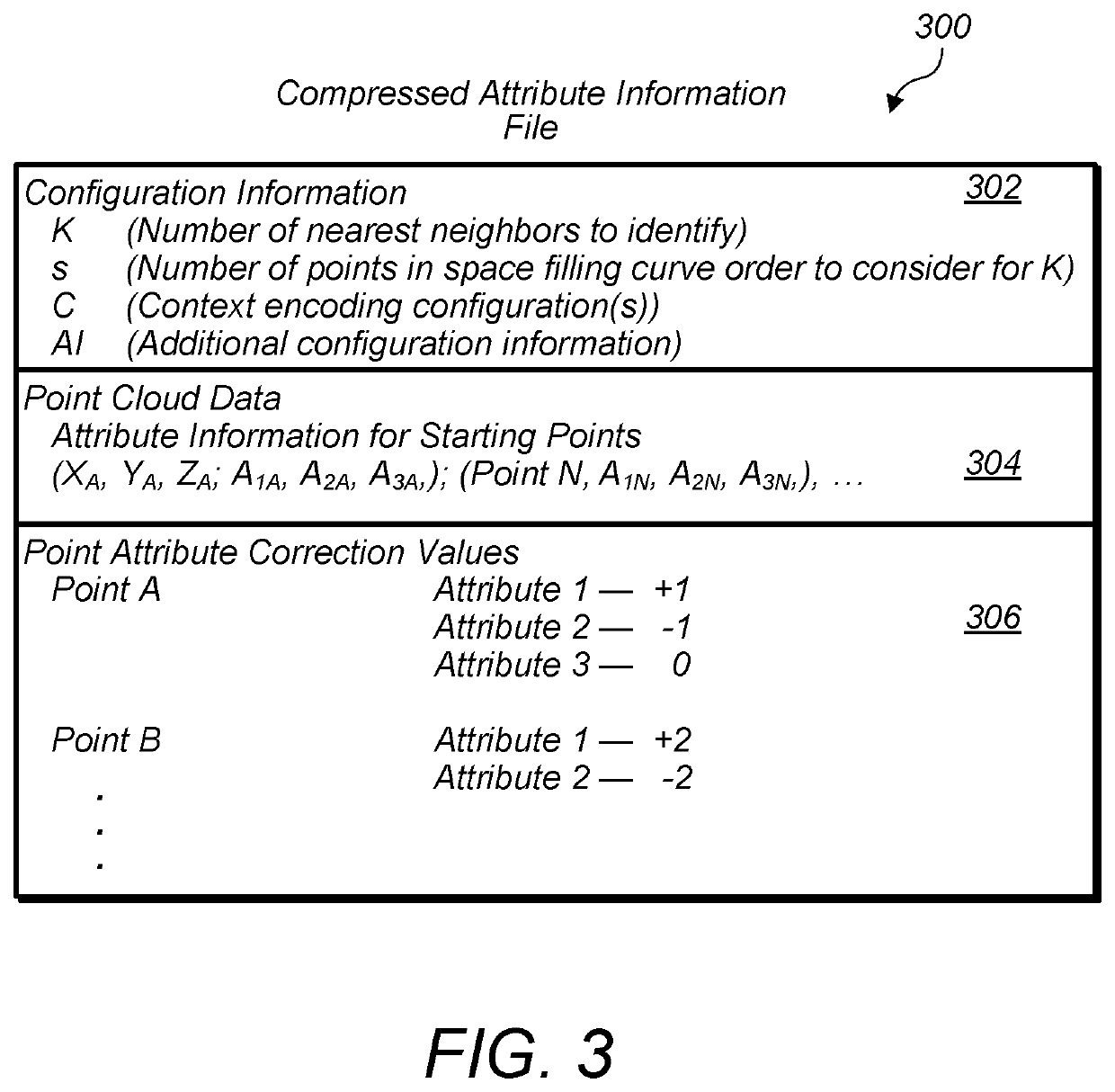
Predicting attributes for point cloud compression according to a space filling curve
PatentActiveUS11132818B2
Innovation
- A system that uses an encoder to compress attribute and spatial information of point clouds using a space filling curve, allowing for real-time or near real-time transmission and storage by predicting attribute values based on spatial information through interpolation-based methods, such as inverse-distance interpolation, and encoding these predictions along with spatial information.
Computational Resources and Infrastructure Requirements
The implementation of advanced experimental design methods for Multi-fidelity Approximation Problems (MAPs) necessitates substantial computational resources and infrastructure. High-performance computing (HPC) clusters are essential for executing complex adaptive sampling algorithms, particularly when dealing with large-scale engineering simulations. These systems typically require multi-core processors with at least 32-64 cores per node and a minimum of 128GB RAM to efficiently handle the matrix operations involved in surrogate model construction and validation.
Storage requirements are equally significant, with datasets often reaching terabyte scale when multiple fidelity levels are incorporated. Distributed file systems like Lustre or GPFS are recommended to manage these large datasets efficiently while maintaining high throughput for parallel access. For organizations implementing these experimental design frameworks, investment in GPU acceleration becomes increasingly important, particularly for deep learning-based surrogate models that benefit from NVIDIA A100 or similar tensor core architectures.
Network infrastructure must support high-bandwidth, low-latency communication between compute nodes, with InfiniBand or equivalent technologies (minimum 100 Gbps) being standard for efficient parallel processing of adaptive sampling workflows. Cloud-based alternatives like AWS HPC instances or Azure HPC can provide scalable solutions for organizations without dedicated infrastructure, though careful cost analysis is necessary as extended simulation campaigns can incur significant expenses.
Software requirements include specialized libraries for experimental design (e.g., PyDOE2, DiceDesign), surrogate modeling frameworks (e.g., GPyTorch, SMT), and optimization tools (e.g., Dakota, OpenMDAO). Container technologies such as Singularity or Docker are increasingly utilized to ensure reproducibility across different computing environments, particularly important when integrating multi-fidelity data from various sources.
For real-time adaptive sampling implementations, dedicated visualization nodes with specialized hardware are recommended to monitor convergence metrics and sampling decisions. These typically require workstation-grade GPUs and high-resolution displays. Organizations should also consider implementing automated workflow management systems like Airflow or Luigi to orchestrate the complex pipeline from simulation execution to model updating and subsequent sample selection.
The computational demands scale non-linearly with problem dimensionality, with high-dimensional problems (>20 variables) potentially requiring specialized dimension reduction techniques implemented on dedicated hardware to remain tractable. Finally, data security infrastructure must be robust, particularly when proprietary simulation codes or sensitive design data are involved in the experimental design process.
Storage requirements are equally significant, with datasets often reaching terabyte scale when multiple fidelity levels are incorporated. Distributed file systems like Lustre or GPFS are recommended to manage these large datasets efficiently while maintaining high throughput for parallel access. For organizations implementing these experimental design frameworks, investment in GPU acceleration becomes increasingly important, particularly for deep learning-based surrogate models that benefit from NVIDIA A100 or similar tensor core architectures.
Network infrastructure must support high-bandwidth, low-latency communication between compute nodes, with InfiniBand or equivalent technologies (minimum 100 Gbps) being standard for efficient parallel processing of adaptive sampling workflows. Cloud-based alternatives like AWS HPC instances or Azure HPC can provide scalable solutions for organizations without dedicated infrastructure, though careful cost analysis is necessary as extended simulation campaigns can incur significant expenses.
Software requirements include specialized libraries for experimental design (e.g., PyDOE2, DiceDesign), surrogate modeling frameworks (e.g., GPyTorch, SMT), and optimization tools (e.g., Dakota, OpenMDAO). Container technologies such as Singularity or Docker are increasingly utilized to ensure reproducibility across different computing environments, particularly important when integrating multi-fidelity data from various sources.
For real-time adaptive sampling implementations, dedicated visualization nodes with specialized hardware are recommended to monitor convergence metrics and sampling decisions. These typically require workstation-grade GPUs and high-resolution displays. Organizations should also consider implementing automated workflow management systems like Airflow or Luigi to orchestrate the complex pipeline from simulation execution to model updating and subsequent sample selection.
The computational demands scale non-linearly with problem dimensionality, with high-dimensional problems (>20 variables) potentially requiring specialized dimension reduction techniques implemented on dedicated hardware to remain tractable. Finally, data security infrastructure must be robust, particularly when proprietary simulation codes or sensitive design data are involved in the experimental design process.
Statistical Validation Methods for MAP Experiment Results
Statistical validation is essential for ensuring the reliability and reproducibility of MAP (Model-Assisted Planning) experiment results. Traditional validation methods often fall short when applied to complex MAP experiments, necessitating specialized approaches that account for the unique characteristics of space-filling and adaptive sampling methodologies.
Cross-validation techniques have been adapted specifically for MAP experiments, with k-fold validation being particularly effective for evaluating the robustness of adaptive sampling strategies. This approach involves partitioning the experimental data into k subsets, using k-1 subsets for model training and the remaining subset for validation. When applied to MAP experiments, special attention must be paid to maintaining the spatial distribution properties of the original dataset during partitioning.
Bootstrap resampling methods offer another powerful validation approach for MAP experiments. By generating multiple resampled datasets from the original experimental data, researchers can assess the stability of their models and quantify uncertainty in their results. For adaptive sampling strategies, modified bootstrap techniques that preserve the sequential nature of the sampling process have shown superior performance compared to standard bootstrapping.
Statistical power analysis plays a crucial role in validating MAP experiment results, particularly when determining the minimum sample size required to detect meaningful effects. For space-filling designs, power calculations must account for the spatial distribution of sampling points, while adaptive sampling strategies require dynamic power analysis methods that adjust as the experiment progresses.
Residual analysis techniques have been extended to accommodate the non-uniform sampling distributions characteristic of adaptive MAP experiments. Specialized residual plots that account for sampling density variations can reveal patterns that might be obscured by traditional residual analysis methods. Additionally, heteroscedasticity tests modified for adaptive sampling contexts help ensure the validity of statistical inferences.
Bayesian validation frameworks have emerged as particularly valuable for MAP experiments, as they naturally incorporate prior knowledge and uncertainty quantification. These frameworks allow for the continuous updating of validation metrics as new data points are added through adaptive sampling, providing a more coherent approach to validation throughout the experimental process.
Recent advances in computational validation methods, including permutation tests and simulation-based inference, have further enhanced our ability to validate MAP experiment results under complex sampling schemes. These methods are especially valuable when theoretical distributions are difficult to determine or when experimental designs deviate significantly from classical assumptions.
Cross-validation techniques have been adapted specifically for MAP experiments, with k-fold validation being particularly effective for evaluating the robustness of adaptive sampling strategies. This approach involves partitioning the experimental data into k subsets, using k-1 subsets for model training and the remaining subset for validation. When applied to MAP experiments, special attention must be paid to maintaining the spatial distribution properties of the original dataset during partitioning.
Bootstrap resampling methods offer another powerful validation approach for MAP experiments. By generating multiple resampled datasets from the original experimental data, researchers can assess the stability of their models and quantify uncertainty in their results. For adaptive sampling strategies, modified bootstrap techniques that preserve the sequential nature of the sampling process have shown superior performance compared to standard bootstrapping.
Statistical power analysis plays a crucial role in validating MAP experiment results, particularly when determining the minimum sample size required to detect meaningful effects. For space-filling designs, power calculations must account for the spatial distribution of sampling points, while adaptive sampling strategies require dynamic power analysis methods that adjust as the experiment progresses.
Residual analysis techniques have been extended to accommodate the non-uniform sampling distributions characteristic of adaptive MAP experiments. Specialized residual plots that account for sampling density variations can reveal patterns that might be obscured by traditional residual analysis methods. Additionally, heteroscedasticity tests modified for adaptive sampling contexts help ensure the validity of statistical inferences.
Bayesian validation frameworks have emerged as particularly valuable for MAP experiments, as they naturally incorporate prior knowledge and uncertainty quantification. These frameworks allow for the continuous updating of validation metrics as new data points are added through adaptive sampling, providing a more coherent approach to validation throughout the experimental process.
Recent advances in computational validation methods, including permutation tests and simulation-based inference, have further enhanced our ability to validate MAP experiment results under complex sampling schemes. These methods are especially valuable when theoretical distributions are difficult to determine or when experimental designs deviate significantly from classical assumptions.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!