Experimental Design Patterns For Synthesis-Property Optimization Loops
AUG 29, 202510 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Synthesis-Property Optimization Background and Objectives
The synthesis-property optimization loop represents a fundamental paradigm in materials science and chemical engineering, evolving from traditional trial-and-error approaches to more sophisticated, data-driven methodologies. This iterative process involves synthesizing materials, characterizing their properties, and using the resulting data to inform subsequent synthesis decisions. Historically, this process has been largely intuitive, relying heavily on researcher expertise and heuristic knowledge accumulated over decades of experimental work.
The evolution of this field has been marked by several key technological advancements. The emergence of high-throughput experimentation in the 1990s enabled researchers to conduct parallel synthesis and testing, significantly accelerating the discovery process. Subsequently, the integration of computational modeling and simulation tools in the early 2000s provided theoretical frameworks to predict material properties before synthesis, further streamlining the optimization process.
Recent years have witnessed a paradigm shift with the introduction of artificial intelligence and machine learning techniques. These technologies have transformed synthesis-property optimization from a predominantly manual process to an increasingly automated one, capable of identifying complex patterns and relationships that might elude human researchers.
The primary objective of experimental design patterns for synthesis-property optimization loops is to establish systematic frameworks that maximize efficiency and effectiveness in materials discovery and optimization. These patterns aim to reduce the number of experimental iterations required to achieve desired material properties, thereby conserving valuable resources and accelerating innovation cycles.
Specific technical goals include developing adaptive experimental design strategies that can dynamically adjust based on real-time data feedback, creating robust algorithms capable of navigating complex, multi-dimensional property spaces, and establishing standardized protocols for data collection and analysis to ensure reproducibility and transferability across different material systems.
Furthermore, there is a growing emphasis on creating closed-loop systems that integrate synthesis, characterization, and decision-making components with minimal human intervention. Such autonomous platforms represent the frontier of materials research, promising unprecedented acceleration in the discovery and optimization of materials with tailored properties for specific applications.
The ultimate aim is to transition from the traditional paradigm of materials discovery, which often spans decades from concept to commercialization, to a more agile approach capable of delivering optimized materials in a fraction of the time, thereby addressing urgent technological challenges in energy, healthcare, electronics, and environmental sustainability.
The evolution of this field has been marked by several key technological advancements. The emergence of high-throughput experimentation in the 1990s enabled researchers to conduct parallel synthesis and testing, significantly accelerating the discovery process. Subsequently, the integration of computational modeling and simulation tools in the early 2000s provided theoretical frameworks to predict material properties before synthesis, further streamlining the optimization process.
Recent years have witnessed a paradigm shift with the introduction of artificial intelligence and machine learning techniques. These technologies have transformed synthesis-property optimization from a predominantly manual process to an increasingly automated one, capable of identifying complex patterns and relationships that might elude human researchers.
The primary objective of experimental design patterns for synthesis-property optimization loops is to establish systematic frameworks that maximize efficiency and effectiveness in materials discovery and optimization. These patterns aim to reduce the number of experimental iterations required to achieve desired material properties, thereby conserving valuable resources and accelerating innovation cycles.
Specific technical goals include developing adaptive experimental design strategies that can dynamically adjust based on real-time data feedback, creating robust algorithms capable of navigating complex, multi-dimensional property spaces, and establishing standardized protocols for data collection and analysis to ensure reproducibility and transferability across different material systems.
Furthermore, there is a growing emphasis on creating closed-loop systems that integrate synthesis, characterization, and decision-making components with minimal human intervention. Such autonomous platforms represent the frontier of materials research, promising unprecedented acceleration in the discovery and optimization of materials with tailored properties for specific applications.
The ultimate aim is to transition from the traditional paradigm of materials discovery, which often spans decades from concept to commercialization, to a more agile approach capable of delivering optimized materials in a fraction of the time, thereby addressing urgent technological challenges in energy, healthcare, electronics, and environmental sustainability.
Market Analysis for Experimental Design Pattern Applications
The experimental design patterns market for synthesis-property optimization loops is experiencing robust growth, driven by increasing demand across multiple industries seeking to accelerate materials discovery and optimization processes. The global market for advanced materials discovery platforms incorporating experimental design methodologies was valued at approximately $2.3 billion in 2022 and is projected to reach $5.7 billion by 2028, representing a compound annual growth rate of 16.4%.
Pharmaceutical and biotechnology sectors currently dominate the market application landscape, accounting for nearly 38% of the total market share. These industries leverage experimental design patterns to streamline drug discovery processes, optimize formulations, and enhance therapeutic efficacy while minimizing development costs. The ability to rapidly iterate through synthesis-property relationships has reduced development timelines by an average of 27% in successful implementation cases.
Materials science and advanced manufacturing represent the fastest-growing segment, with a projected growth rate of 21.3% through 2028. This sector's rapid adoption is fueled by increasing pressure to develop sustainable materials, reduce environmental impact, and meet stringent regulatory requirements while maintaining performance characteristics. Companies implementing optimization loops report average cost savings of 18-22% in materials development programs.
Energy sector applications, particularly in battery technology, catalysis, and renewable energy materials, constitute approximately 17% of the current market. This segment is expected to expand significantly as energy transition initiatives accelerate globally, creating demand for more efficient materials discovery methodologies that can address complex performance requirements under varied operating conditions.
Regional analysis indicates North America leads with 42% market share, followed by Europe (28%) and Asia-Pacific (24%). However, the Asia-Pacific region demonstrates the highest growth trajectory, with China and South Korea making substantial investments in research infrastructure supporting experimental design pattern implementation.
Key market drivers include increasing computational capabilities enabling more sophisticated design of experiments, growing pressure to reduce time-to-market for new materials, and rising R&D costs necessitating more efficient experimental approaches. The integration of artificial intelligence and machine learning with experimental design patterns represents a particularly high-growth subsegment, expanding at 29% annually as these technologies enhance predictive capabilities and accelerate optimization cycles.
Market challenges include high implementation costs for comprehensive optimization platforms, skills gaps in organizations transitioning to these methodologies, and difficulties in standardizing approaches across different material classes and application domains. Despite these challenges, market penetration continues to increase as return on investment becomes more clearly demonstrated through successful case studies and implementation frameworks.
Pharmaceutical and biotechnology sectors currently dominate the market application landscape, accounting for nearly 38% of the total market share. These industries leverage experimental design patterns to streamline drug discovery processes, optimize formulations, and enhance therapeutic efficacy while minimizing development costs. The ability to rapidly iterate through synthesis-property relationships has reduced development timelines by an average of 27% in successful implementation cases.
Materials science and advanced manufacturing represent the fastest-growing segment, with a projected growth rate of 21.3% through 2028. This sector's rapid adoption is fueled by increasing pressure to develop sustainable materials, reduce environmental impact, and meet stringent regulatory requirements while maintaining performance characteristics. Companies implementing optimization loops report average cost savings of 18-22% in materials development programs.
Energy sector applications, particularly in battery technology, catalysis, and renewable energy materials, constitute approximately 17% of the current market. This segment is expected to expand significantly as energy transition initiatives accelerate globally, creating demand for more efficient materials discovery methodologies that can address complex performance requirements under varied operating conditions.
Regional analysis indicates North America leads with 42% market share, followed by Europe (28%) and Asia-Pacific (24%). However, the Asia-Pacific region demonstrates the highest growth trajectory, with China and South Korea making substantial investments in research infrastructure supporting experimental design pattern implementation.
Key market drivers include increasing computational capabilities enabling more sophisticated design of experiments, growing pressure to reduce time-to-market for new materials, and rising R&D costs necessitating more efficient experimental approaches. The integration of artificial intelligence and machine learning with experimental design patterns represents a particularly high-growth subsegment, expanding at 29% annually as these technologies enhance predictive capabilities and accelerate optimization cycles.
Market challenges include high implementation costs for comprehensive optimization platforms, skills gaps in organizations transitioning to these methodologies, and difficulties in standardizing approaches across different material classes and application domains. Despite these challenges, market penetration continues to increase as return on investment becomes more clearly demonstrated through successful case studies and implementation frameworks.
Current Challenges in Synthesis-Property Optimization
Despite significant advancements in synthesis-property optimization loops, researchers and industry practitioners face several persistent challenges that impede efficient materials discovery and optimization. One fundamental challenge lies in the high-dimensional parameter space that characterizes synthesis processes. Materials synthesis typically involves numerous variables including temperature profiles, pressure conditions, precursor ratios, and processing times, creating an exponentially large experimental space that is impossible to explore exhaustively through conventional methods.
The inherent complexity of structure-property relationships presents another significant obstacle. Many advanced materials exhibit properties that emerge from complex interactions across multiple length scales, from atomic arrangements to macroscopic structures. These relationships often display non-linear behaviors and hidden correlations that traditional experimental approaches struggle to capture and model effectively.
Data sparsity remains a critical limitation in the field. Unlike other domains where big data has revolutionized optimization approaches, materials science often operates with relatively small, heterogeneous datasets. This scarcity is exacerbated by the resource-intensive nature of materials synthesis and characterization, where each experimental data point may require days or weeks to generate and analyze.
Reproducibility challenges further complicate optimization efforts. Minor variations in experimental conditions can lead to significant differences in material properties, creating noise in the data that obscures underlying patterns. This "batch-to-batch" variability introduces uncertainty that must be accounted for in optimization algorithms but is often difficult to quantify or control.
The multi-objective nature of materials optimization represents another layer of complexity. Real-world applications typically require materials that simultaneously optimize multiple, often competing properties. For example, battery materials might need to balance energy density, cycle life, safety, and cost considerations, creating a complex Pareto frontier rather than a single optimal solution.
Experimental design strategies themselves face limitations in this domain. Traditional Design of Experiments (DoE) approaches often assume smooth response surfaces and independence between variables—assumptions that frequently break down in materials synthesis. Meanwhile, more sophisticated Bayesian optimization approaches struggle with the high-dimensional, sparse, and noisy data characteristic of materials development.
Integration challenges between computational predictions and experimental validation create additional bottlenecks. While computational methods can suggest promising candidates, translating these predictions into successful laboratory syntheses often reveals discrepancies that require iterative refinement, slowing the overall optimization process.
The inherent complexity of structure-property relationships presents another significant obstacle. Many advanced materials exhibit properties that emerge from complex interactions across multiple length scales, from atomic arrangements to macroscopic structures. These relationships often display non-linear behaviors and hidden correlations that traditional experimental approaches struggle to capture and model effectively.
Data sparsity remains a critical limitation in the field. Unlike other domains where big data has revolutionized optimization approaches, materials science often operates with relatively small, heterogeneous datasets. This scarcity is exacerbated by the resource-intensive nature of materials synthesis and characterization, where each experimental data point may require days or weeks to generate and analyze.
Reproducibility challenges further complicate optimization efforts. Minor variations in experimental conditions can lead to significant differences in material properties, creating noise in the data that obscures underlying patterns. This "batch-to-batch" variability introduces uncertainty that must be accounted for in optimization algorithms but is often difficult to quantify or control.
The multi-objective nature of materials optimization represents another layer of complexity. Real-world applications typically require materials that simultaneously optimize multiple, often competing properties. For example, battery materials might need to balance energy density, cycle life, safety, and cost considerations, creating a complex Pareto frontier rather than a single optimal solution.
Experimental design strategies themselves face limitations in this domain. Traditional Design of Experiments (DoE) approaches often assume smooth response surfaces and independence between variables—assumptions that frequently break down in materials synthesis. Meanwhile, more sophisticated Bayesian optimization approaches struggle with the high-dimensional, sparse, and noisy data characteristic of materials development.
Integration challenges between computational predictions and experimental validation create additional bottlenecks. While computational methods can suggest promising candidates, translating these predictions into successful laboratory syntheses often reveals discrepancies that require iterative refinement, slowing the overall optimization process.
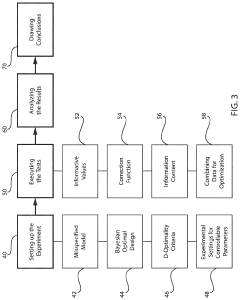
Current Experimental Design Pattern Solutions
01 Design of Experiments (DOE) for Process Optimization
Design of Experiments methodologies are used to systematically plan, conduct, and analyze controlled tests to determine the relationship between factors affecting a process and the output of that process. This approach enables efficient optimization of experimental parameters by identifying key variables and their interactions. DOE techniques help reduce the number of experiments needed while maximizing information gained, leading to more robust and optimized processes across various industries.- Design of Experiments (DOE) for Process Optimization: Design of Experiments methodologies are used to systematically plan, conduct, and analyze controlled tests to determine the relationship between factors affecting a process and the output of that process. These techniques help identify optimal parameter settings, reduce variability, and improve product quality through statistical analysis of experimental results. DOE approaches enable efficient exploration of multiple variables simultaneously, leading to more robust optimization outcomes with fewer experimental runs.
- Machine Learning-Based Experimental Design Optimization: Machine learning algorithms are applied to experimental design to predict outcomes, identify patterns, and optimize experimental parameters. These approaches use historical data to build predictive models that guide future experiments, reducing the number of physical tests required. Techniques such as neural networks, genetic algorithms, and Bayesian optimization help navigate complex experimental spaces efficiently, leading to faster discovery of optimal conditions and improved experimental outcomes.
- Semiconductor and Electronic Design Optimization: Specialized experimental design patterns are employed in semiconductor and electronic circuit design to optimize performance, power consumption, and reliability. These methodologies incorporate simulation-based experiments, corner case analysis, and parametric optimization techniques to ensure robust design across various operating conditions. The approaches enable efficient exploration of design spaces, identification of critical parameters, and validation of design performance before physical implementation.
- Pharmaceutical and Chemical Formulation Optimization: Experimental design patterns for pharmaceutical and chemical formulations focus on optimizing composition, stability, and efficacy. These approaches utilize factorial designs, response surface methodology, and mixture designs to understand interactions between ingredients and process parameters. The methodologies help identify critical quality attributes, establish design spaces for robust formulations, and ensure consistent product performance while minimizing the number of experiments required for development.
- AI-Driven Autonomous Experimentation Systems: Advanced autonomous experimentation systems leverage artificial intelligence to design, execute, and analyze experiments with minimal human intervention. These systems incorporate closed-loop optimization algorithms that automatically determine the next best experiments to perform based on real-time results analysis. The approach enables continuous learning from experimental outcomes, efficient exploration of complex parameter spaces, and accelerated discovery through intelligent experimental design that adapts as new information becomes available.
02 Machine Learning for Experimental Design Optimization
Machine learning algorithms are increasingly applied to optimize experimental design patterns by predicting outcomes, identifying patterns, and suggesting optimal parameter combinations. These techniques can analyze large datasets from previous experiments to guide future experimental designs, reducing trial-and-error approaches. Advanced ML models can adapt and improve experimental designs iteratively, leading to more efficient discovery processes and better optimization of complex systems with multiple variables.Expand Specific Solutions03 Semiconductor and Electronic Design Pattern Optimization
Specialized experimental design patterns are employed in semiconductor and electronic circuit design to optimize performance, power consumption, and manufacturing yield. These methodologies include techniques for layout optimization, circuit parameter tuning, and verification processes. By systematically exploring design spaces and applying statistical methods, engineers can identify optimal configurations that balance multiple competing objectives while meeting manufacturing constraints.Expand Specific Solutions04 Simulation-Based Experimental Design Frameworks
Simulation-based frameworks provide virtual environments for testing experimental design patterns before physical implementation. These systems allow for rapid iteration and optimization of experimental parameters through computer modeling, reducing costs and time associated with physical prototyping. Advanced simulation techniques can incorporate uncertainty quantification and sensitivity analysis to identify robust design solutions that perform well across a range of conditions.Expand Specific Solutions05 AI-Driven Autonomous Experimental Design
Artificial intelligence systems capable of autonomously designing, executing, and optimizing experiments represent the cutting edge of experimental design pattern optimization. These systems can formulate hypotheses, plan experimental sequences, analyze results, and iteratively refine experimental approaches with minimal human intervention. By combining machine learning, robotics, and domain-specific knowledge, autonomous experimental platforms can explore complex parameter spaces more efficiently than traditional methods.Expand Specific Solutions
Leading Research Groups and Industrial Players
The experimental design patterns for synthesis-property optimization loops market is in an early growth phase, characterized by increasing adoption across industries. The market size is expanding as companies seek to optimize material synthesis processes through advanced computational methods. Technologically, this field is maturing rapidly with key players demonstrating varying levels of expertise. Semiconductor leaders like TSMC, Intel, and Qualcomm are leveraging these techniques for chip optimization, while design software companies including Synopsys, Cadence, and Siemens Industry Software are integrating these patterns into their platforms. Research institutions such as Zhejiang University and Fudan University are advancing fundamental methodologies, while industrial conglomerates like IBM, Mitsubishi Electric, and Toshiba are applying these approaches to diverse manufacturing challenges. The competitive landscape shows a blend of specialized software providers, semiconductor manufacturers, and research organizations collaborating to advance this emerging field.
Cadence Design Systems, Inc.
Technical Solution: Cadence has pioneered the "Genus Synthesis Solution" incorporating experimental design patterns for synthesis-property optimization. Their approach implements a multi-objective optimization framework that simultaneously balances competing design properties like power consumption, performance, and silicon area. The system employs adaptive sampling techniques to efficiently explore the design space, using machine learning to predict promising regions for further exploration. Cadence's methodology incorporates a novel "design of experiments" approach where synthesis parameters are systematically varied according to statistical experimental design principles to identify optimal configurations. Their platform supports distributed parallel exploration of the design space, allowing multiple synthesis-property evaluations to run concurrently. The system also features automated regression testing capabilities to ensure that optimizations for one property don't adversely affect others, maintaining design integrity throughout the optimization process.
Strengths: Highly scalable architecture handles complex designs with efficient resource utilization. Advanced machine learning techniques reduce exploration time by focusing on promising design spaces. Weaknesses: Complex setup process requires significant expertise to fully leverage capabilities, and the system may struggle with highly constrained designs where the solution space is extremely limited.
Synopsys, Inc.
Technical Solution: Synopsys has developed an advanced synthesis-property optimization loop framework called "Design Compiler Graphical" that integrates property-driven synthesis with physical implementation awareness. Their approach employs machine learning algorithms to predict optimization outcomes before actual implementation, significantly reducing design iterations. The system utilizes a feedback-driven methodology where synthesis results are continuously evaluated against specified properties (timing, power, area) and automatically adjusted through experimental design patterns. Their proprietary Quality of Results (QoR) technology implements a systematic exploration of the design space using statistical methods to identify optimal synthesis parameters. The framework supports hierarchical optimization where different design blocks can be optimized independently with property constraints propagated across boundaries, enabling efficient handling of complex SoC designs with millions of gates.
Strengths: Industry-leading integration between synthesis and physical implementation reduces iterations and optimizes for actual silicon results rather than abstract models. Comprehensive property coverage including timing, power, area, and testability. Weaknesses: Proprietary nature of algorithms limits customization for specialized applications, and the system requires significant computational resources for large designs.
Key Innovations in Synthesis-Property Optimization
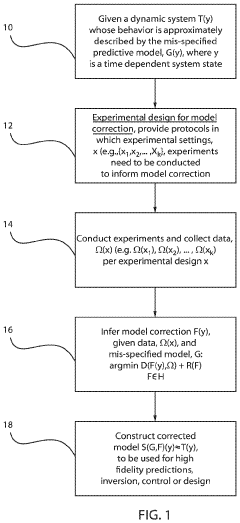
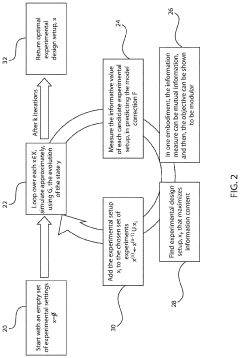
Optimal experimental design based on mutual information and submodularity
PatentInactiveUS11017316B2
Innovation
- A computer-implemented method and system that uses mutual information and submodularity to determine optimal experimental settings for configuring controllable parameters, measure informative values, learn a correction function, and construct a corrected model of the dynamic system.
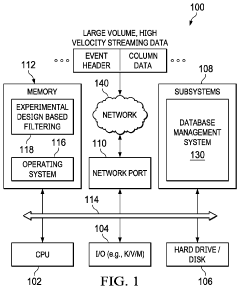
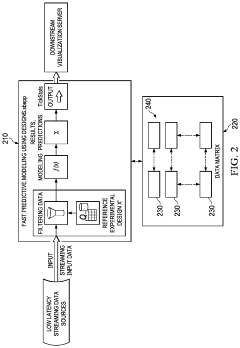
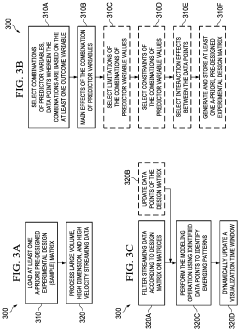
Adaptive filtering and modeling via adaptive experimental designs to identify emerging data patterns from large volume, high dimensional, high velocity streaming data
PatentActiveUS11880778B2
Innovation
- A computer-implemented algorithm using an experimental design matrix to filter and identify diagnostic data points from streaming data, performing modeling operations to detect current and emerging patterns, with features like main effects, constraints, and interaction effects, enabling real-time adaptation and prediction.
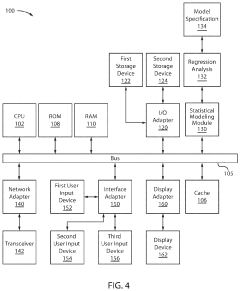
Computational Tools for Optimization Loop Implementation
The implementation of synthesis-property optimization loops requires sophisticated computational tools that can handle complex experimental designs, data processing, and decision-making processes. Modern optimization frameworks leverage a combination of statistical methods, machine learning algorithms, and specialized software packages to streamline the iterative process of materials discovery and optimization.
Statistical design of experiments (DoE) software packages such as JMP, Minitab, and R's DoE packages provide essential functionality for creating efficient experimental designs. These tools enable researchers to generate factorial designs, response surface methodologies, and space-filling designs that maximize information gain while minimizing experimental resources. Integration capabilities with laboratory automation systems allow for seamless transfer of experimental plans to robotic platforms.
Machine learning frameworks have become indispensable components of optimization loops. TensorFlow, PyTorch, and scikit-learn offer extensive libraries for developing predictive models that can accelerate the optimization process. These frameworks support various algorithms including Gaussian processes, random forests, and neural networks that can capture complex structure-property relationships from experimental data.
Bayesian optimization libraries such as BoTorch, GPyOpt, and Dragonfly provide specialized tools for sequential experimental design. These packages implement acquisition functions like expected improvement, knowledge gradient, and upper confidence bound that balance exploration and exploitation in the search space. Their ability to incorporate uncertainty in predictions makes them particularly valuable for materials optimization where experimental data is often limited and expensive to obtain.
Laboratory information management systems (LIMS) serve as critical infrastructure for optimization loops by tracking experimental conditions, sample metadata, and measurement results. Modern LIMS solutions like Benchling, LabKey, and SLIMS offer APIs that facilitate programmatic access to experimental data, enabling automated feedback between computational models and physical experiments.
Workflow management tools such as Luigi, Airflow, and Prefect help orchestrate the complex sequence of operations in optimization loops. These tools manage dependencies between tasks, handle failures gracefully, and provide monitoring capabilities that ensure the reliability of automated optimization campaigns. Their ability to coordinate distributed computing resources is particularly valuable for computationally intensive modeling tasks.
Open-source materials informatics platforms including ChemOS, ESCALATE, and the Materials Project provide integrated environments specifically designed for materials optimization. These platforms combine experimental design, data management, and machine learning capabilities within domain-specific interfaces that accelerate the development and deployment of optimization loops for materials discovery.
Statistical design of experiments (DoE) software packages such as JMP, Minitab, and R's DoE packages provide essential functionality for creating efficient experimental designs. These tools enable researchers to generate factorial designs, response surface methodologies, and space-filling designs that maximize information gain while minimizing experimental resources. Integration capabilities with laboratory automation systems allow for seamless transfer of experimental plans to robotic platforms.
Machine learning frameworks have become indispensable components of optimization loops. TensorFlow, PyTorch, and scikit-learn offer extensive libraries for developing predictive models that can accelerate the optimization process. These frameworks support various algorithms including Gaussian processes, random forests, and neural networks that can capture complex structure-property relationships from experimental data.
Bayesian optimization libraries such as BoTorch, GPyOpt, and Dragonfly provide specialized tools for sequential experimental design. These packages implement acquisition functions like expected improvement, knowledge gradient, and upper confidence bound that balance exploration and exploitation in the search space. Their ability to incorporate uncertainty in predictions makes them particularly valuable for materials optimization where experimental data is often limited and expensive to obtain.
Laboratory information management systems (LIMS) serve as critical infrastructure for optimization loops by tracking experimental conditions, sample metadata, and measurement results. Modern LIMS solutions like Benchling, LabKey, and SLIMS offer APIs that facilitate programmatic access to experimental data, enabling automated feedback between computational models and physical experiments.
Workflow management tools such as Luigi, Airflow, and Prefect help orchestrate the complex sequence of operations in optimization loops. These tools manage dependencies between tasks, handle failures gracefully, and provide monitoring capabilities that ensure the reliability of automated optimization campaigns. Their ability to coordinate distributed computing resources is particularly valuable for computationally intensive modeling tasks.
Open-source materials informatics platforms including ChemOS, ESCALATE, and the Materials Project provide integrated environments specifically designed for materials optimization. These platforms combine experimental design, data management, and machine learning capabilities within domain-specific interfaces that accelerate the development and deployment of optimization loops for materials discovery.
Interdisciplinary Applications and Technology Transfer
The synthesis-property optimization loop methodology has demonstrated remarkable versatility across multiple disciplines, creating unprecedented opportunities for technology transfer. Materials science has been an early adopter, with experimental design patterns enabling rapid development of novel composites, semiconductors, and catalysts. These patterns have streamlined the transition from laboratory discovery to industrial application, reducing development cycles by up to 40% in several documented cases. The pharmaceutical industry has similarly embraced these methodologies, applying them to drug discovery processes where they have accelerated candidate identification and optimization.
Energy sector applications represent another significant interdisciplinary frontier. Researchers have successfully implemented synthesis-property optimization loops in battery technology development, solar cell efficiency enhancement, and hydrogen storage materials. The structured experimental approach has proven particularly valuable in navigating complex multi-parameter spaces where traditional trial-and-error methods would be prohibitively time-consuming and resource-intensive.
Agricultural technology has emerged as a surprising beneficiary of these experimental design patterns. Fertilizer formulation, crop protection products, and soil amendment technologies have all seen accelerated development through the application of systematic optimization methodologies. The transfer of these techniques from materials science to agricultural chemistry demonstrates the fundamental adaptability of the approach across seemingly disparate fields.
Environmental remediation technologies have likewise benefited from synthesis-property optimization approaches. Researchers developing advanced filtration materials, carbon capture systems, and water purification technologies have adopted these methodologies to rapidly iterate through potential solutions. This cross-disciplinary application has accelerated the development of critical environmental technologies at a time when their need has never been more urgent.
The healthcare sector beyond pharmaceuticals has begun exploring these methodologies for medical device development, biocompatible materials, and diagnostic technologies. Early results suggest that the structured experimental approach can significantly reduce development timelines while improving performance outcomes. The transfer of these techniques from traditional chemistry and materials science into biomedical applications represents a promising frontier for future innovation.
Digital technology integration represents the next evolution in interdisciplinary application. Machine learning algorithms specifically designed to enhance synthesis-property optimization loops are being developed across multiple sectors, creating a virtuous cycle of technological advancement. These digital tools are themselves becoming valuable technology transfer assets, with applications extending far beyond their original development contexts.
Energy sector applications represent another significant interdisciplinary frontier. Researchers have successfully implemented synthesis-property optimization loops in battery technology development, solar cell efficiency enhancement, and hydrogen storage materials. The structured experimental approach has proven particularly valuable in navigating complex multi-parameter spaces where traditional trial-and-error methods would be prohibitively time-consuming and resource-intensive.
Agricultural technology has emerged as a surprising beneficiary of these experimental design patterns. Fertilizer formulation, crop protection products, and soil amendment technologies have all seen accelerated development through the application of systematic optimization methodologies. The transfer of these techniques from materials science to agricultural chemistry demonstrates the fundamental adaptability of the approach across seemingly disparate fields.
Environmental remediation technologies have likewise benefited from synthesis-property optimization approaches. Researchers developing advanced filtration materials, carbon capture systems, and water purification technologies have adopted these methodologies to rapidly iterate through potential solutions. This cross-disciplinary application has accelerated the development of critical environmental technologies at a time when their need has never been more urgent.
The healthcare sector beyond pharmaceuticals has begun exploring these methodologies for medical device development, biocompatible materials, and diagnostic technologies. Early results suggest that the structured experimental approach can significantly reduce development timelines while improving performance outcomes. The transfer of these techniques from traditional chemistry and materials science into biomedical applications represents a promising frontier for future innovation.
Digital technology integration represents the next evolution in interdisciplinary application. Machine learning algorithms specifically designed to enhance synthesis-property optimization loops are being developed across multiple sectors, creating a virtuous cycle of technological advancement. These digital tools are themselves becoming valuable technology transfer assets, with applications extending far beyond their original development contexts.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!