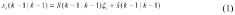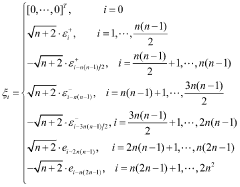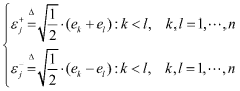Kalman Filter Vs Nonparametric Estimation Techniques: Performance
SEP 12, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Kalman Filter and Nonparametric Estimation Background
The Kalman filter, developed by Rudolf E. Kalman in 1960, represents a significant milestone in estimation theory. Originally designed for aerospace applications during the Apollo program, this recursive algorithm optimally estimates states of dynamic systems from noisy measurements. The filter operates on a predict-correct cycle, where system state is predicted based on previous estimates and then corrected using new measurements, weighted by the Kalman gain.
Over decades, various adaptations have emerged, including Extended Kalman Filter (EKF) for nonlinear systems, Unscented Kalman Filter (UKF) for highly nonlinear applications, and Ensemble Kalman Filter (EnKF) for high-dimensional systems. These variants maintain the core principles while addressing specific limitations of the original formulation.
Nonparametric estimation techniques emerged as alternatives that make fewer assumptions about underlying data distributions. Particle filters (Sequential Monte Carlo methods), introduced in the 1990s, represent probability distributions through discrete samples, making them suitable for non-Gaussian and highly nonlinear systems. These methods excel in multimodal distribution scenarios where Kalman-based approaches struggle.
Kernel density estimation (KDE), another prominent nonparametric technique, estimates probability density functions by placing kernel functions at each data point. Gaussian Process regression offers a flexible framework for modeling unknown functions with uncertainty quantification. These approaches provide greater flexibility but typically demand higher computational resources.
The technical evolution trajectory shows a clear trend from model-dependent methods toward more flexible, data-driven approaches. Early estimation techniques relied heavily on precise mathematical models, while modern nonparametric methods emphasize learning from data with minimal assumptions.
Performance comparison between these approaches reveals fundamental trade-offs. Kalman filters deliver optimal performance when system dynamics match their assumptions (linear systems with Gaussian noise) while maintaining computational efficiency. Nonparametric methods offer greater flexibility for complex, nonlinear systems but at increased computational cost.
Recent research focuses on hybrid approaches that combine the efficiency of Kalman filters with the flexibility of nonparametric methods. These include Rao-Blackwellized particle filters and Gaussian sum filters that represent complex distributions as mixtures of Gaussians.
The technological landscape continues evolving toward adaptive estimation techniques that automatically select optimal approaches based on data characteristics. Machine learning integration with traditional estimation methods represents another frontier, with deep learning being used to model complex system dynamics that traditional filters struggle to capture.
Over decades, various adaptations have emerged, including Extended Kalman Filter (EKF) for nonlinear systems, Unscented Kalman Filter (UKF) for highly nonlinear applications, and Ensemble Kalman Filter (EnKF) for high-dimensional systems. These variants maintain the core principles while addressing specific limitations of the original formulation.
Nonparametric estimation techniques emerged as alternatives that make fewer assumptions about underlying data distributions. Particle filters (Sequential Monte Carlo methods), introduced in the 1990s, represent probability distributions through discrete samples, making them suitable for non-Gaussian and highly nonlinear systems. These methods excel in multimodal distribution scenarios where Kalman-based approaches struggle.
Kernel density estimation (KDE), another prominent nonparametric technique, estimates probability density functions by placing kernel functions at each data point. Gaussian Process regression offers a flexible framework for modeling unknown functions with uncertainty quantification. These approaches provide greater flexibility but typically demand higher computational resources.
The technical evolution trajectory shows a clear trend from model-dependent methods toward more flexible, data-driven approaches. Early estimation techniques relied heavily on precise mathematical models, while modern nonparametric methods emphasize learning from data with minimal assumptions.
Performance comparison between these approaches reveals fundamental trade-offs. Kalman filters deliver optimal performance when system dynamics match their assumptions (linear systems with Gaussian noise) while maintaining computational efficiency. Nonparametric methods offer greater flexibility for complex, nonlinear systems but at increased computational cost.
Recent research focuses on hybrid approaches that combine the efficiency of Kalman filters with the flexibility of nonparametric methods. These include Rao-Blackwellized particle filters and Gaussian sum filters that represent complex distributions as mixtures of Gaussians.
The technological landscape continues evolving toward adaptive estimation techniques that automatically select optimal approaches based on data characteristics. Machine learning integration with traditional estimation methods represents another frontier, with deep learning being used to model complex system dynamics that traditional filters struggle to capture.
Market Applications and Demand Analysis
The market for estimation and filtering technologies has experienced significant growth across multiple sectors, driven by the increasing need for accurate state estimation in dynamic systems. Kalman filters and nonparametric estimation techniques serve distinct market segments based on their performance characteristics and application requirements.
In the autonomous vehicles sector, demand for reliable state estimation solutions has surged, with the market projected to reach $556 billion by 2026. Kalman filters dominate applications requiring real-time processing with limited computational resources, such as vehicle positioning and sensor fusion. However, nonparametric methods are gaining traction in scenarios involving complex, non-Gaussian noise distributions where traditional Kalman approaches underperform.
The aerospace and defense industry represents another substantial market, valued at approximately $298 billion globally. Here, the demand splits between Kalman filters for navigation systems and nonparametric techniques for target tracking in cluttered environments. Military applications particularly value the robustness of nonparametric methods when dealing with adversarial scenarios and intentional signal jamming.
Financial technology applications have embraced both technologies for different purposes. Kalman filters are preferred in high-frequency trading systems where computational efficiency is paramount. Conversely, nonparametric methods have found favor in risk assessment and market prediction models where distribution assumptions can significantly impact performance. This market segment shows a compound annual growth rate of 23.4% as algorithmic trading continues to expand.
Healthcare and biomedical applications represent an emerging market for these technologies. Patient monitoring systems increasingly utilize Kalman filters for vital sign tracking, while nonparametric methods are preferred in diagnostic imaging and disease progression modeling. The medical devices market incorporating these technologies is growing at 15.7% annually.
Industrial IoT applications have created substantial demand for both technologies, with smart manufacturing solutions requiring real-time state estimation for process control and predictive maintenance. The market size for industrial analytics solutions incorporating these technologies exceeds $25 billion and continues to grow as Industry 4.0 adoption accelerates.
Regional analysis reveals North America leading in adoption across most sectors, with Asia-Pacific showing the fastest growth rate, particularly in manufacturing and automotive applications. European markets demonstrate strong demand in precision engineering and aerospace applications, with stringent performance requirements driving technology selection.
In the autonomous vehicles sector, demand for reliable state estimation solutions has surged, with the market projected to reach $556 billion by 2026. Kalman filters dominate applications requiring real-time processing with limited computational resources, such as vehicle positioning and sensor fusion. However, nonparametric methods are gaining traction in scenarios involving complex, non-Gaussian noise distributions where traditional Kalman approaches underperform.
The aerospace and defense industry represents another substantial market, valued at approximately $298 billion globally. Here, the demand splits between Kalman filters for navigation systems and nonparametric techniques for target tracking in cluttered environments. Military applications particularly value the robustness of nonparametric methods when dealing with adversarial scenarios and intentional signal jamming.
Financial technology applications have embraced both technologies for different purposes. Kalman filters are preferred in high-frequency trading systems where computational efficiency is paramount. Conversely, nonparametric methods have found favor in risk assessment and market prediction models where distribution assumptions can significantly impact performance. This market segment shows a compound annual growth rate of 23.4% as algorithmic trading continues to expand.
Healthcare and biomedical applications represent an emerging market for these technologies. Patient monitoring systems increasingly utilize Kalman filters for vital sign tracking, while nonparametric methods are preferred in diagnostic imaging and disease progression modeling. The medical devices market incorporating these technologies is growing at 15.7% annually.
Industrial IoT applications have created substantial demand for both technologies, with smart manufacturing solutions requiring real-time state estimation for process control and predictive maintenance. The market size for industrial analytics solutions incorporating these technologies exceeds $25 billion and continues to grow as Industry 4.0 adoption accelerates.
Regional analysis reveals North America leading in adoption across most sectors, with Asia-Pacific showing the fastest growth rate, particularly in manufacturing and automotive applications. European markets demonstrate strong demand in precision engineering and aerospace applications, with stringent performance requirements driving technology selection.
Current Technical Challenges and Limitations
Despite the proven effectiveness of Kalman filters in state estimation, several technical challenges and limitations persist when comparing them with nonparametric estimation techniques. The fundamental assumption of Gaussian noise distribution in Kalman filters represents a significant constraint in real-world applications where noise often exhibits non-Gaussian characteristics. This limitation becomes particularly problematic in environments with outliers or multimodal distributions, leading to suboptimal performance or even filter divergence.
Computational complexity presents another challenge, especially for Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) when dealing with highly nonlinear systems. The linearization process in EKF introduces approximation errors that can accumulate over time, while UKF's sigma point calculation becomes computationally intensive for high-dimensional state spaces. In contrast, nonparametric methods like particle filters offer greater flexibility but at the cost of substantially increased computational requirements.
Model dependency remains a critical limitation for Kalman-based approaches. These filters require explicit mathematical models of system dynamics and measurement processes, which may be difficult to obtain or accurately formulate in complex real-world scenarios. Nonparametric techniques generally demonstrate greater robustness to model uncertainties but struggle with the curse of dimensionality as state dimensions increase.
Parameter tuning presents ongoing challenges for both approaches. Kalman filters require accurate specification of process and measurement noise covariances, which significantly impact performance but are often difficult to determine precisely. Similarly, nonparametric methods require careful selection of parameters such as bandwidth in kernel density estimation or particle count in particle filters.
Real-time implementation constraints affect both methodologies differently. While Kalman filters offer computational efficiency for linear systems, their extensions for nonlinear applications may struggle to meet strict timing requirements in resource-constrained environments. Nonparametric methods typically demand greater computational resources, limiting their applicability in embedded systems or applications requiring high update rates.
The integration of multiple sensor data streams presents unique challenges for both approaches. Kalman filters provide a structured framework for sensor fusion but may perform poorly when sensor characteristics violate their underlying assumptions. Nonparametric methods offer greater flexibility for heterogeneous sensor integration but require more complex implementation strategies and careful management of computational resources.
Adaptation to changing environmental conditions remains problematic, particularly for standard Kalman implementations with fixed parameters. While adaptive variants exist, they introduce additional complexity and potential stability issues. Nonparametric approaches generally demonstrate better adaptability but at the cost of increased parameter sensitivity and computational overhead.
Computational complexity presents another challenge, especially for Extended Kalman Filters (EKF) and Unscented Kalman Filters (UKF) when dealing with highly nonlinear systems. The linearization process in EKF introduces approximation errors that can accumulate over time, while UKF's sigma point calculation becomes computationally intensive for high-dimensional state spaces. In contrast, nonparametric methods like particle filters offer greater flexibility but at the cost of substantially increased computational requirements.
Model dependency remains a critical limitation for Kalman-based approaches. These filters require explicit mathematical models of system dynamics and measurement processes, which may be difficult to obtain or accurately formulate in complex real-world scenarios. Nonparametric techniques generally demonstrate greater robustness to model uncertainties but struggle with the curse of dimensionality as state dimensions increase.
Parameter tuning presents ongoing challenges for both approaches. Kalman filters require accurate specification of process and measurement noise covariances, which significantly impact performance but are often difficult to determine precisely. Similarly, nonparametric methods require careful selection of parameters such as bandwidth in kernel density estimation or particle count in particle filters.
Real-time implementation constraints affect both methodologies differently. While Kalman filters offer computational efficiency for linear systems, their extensions for nonlinear applications may struggle to meet strict timing requirements in resource-constrained environments. Nonparametric methods typically demand greater computational resources, limiting their applicability in embedded systems or applications requiring high update rates.
The integration of multiple sensor data streams presents unique challenges for both approaches. Kalman filters provide a structured framework for sensor fusion but may perform poorly when sensor characteristics violate their underlying assumptions. Nonparametric methods offer greater flexibility for heterogeneous sensor integration but require more complex implementation strategies and careful management of computational resources.
Adaptation to changing environmental conditions remains problematic, particularly for standard Kalman implementations with fixed parameters. While adaptive variants exist, they introduce additional complexity and potential stability issues. Nonparametric approaches generally demonstrate better adaptability but at the cost of increased parameter sensitivity and computational overhead.
Comparative Analysis of Implementation Approaches
01 Kalman Filter Applications in Communication Systems
Kalman filters are widely used in communication systems for channel estimation, signal tracking, and noise reduction. These applications leverage the filter's ability to provide optimal estimates in linear systems with Gaussian noise. The implementation of Kalman filters in wireless communication networks enhances signal quality, improves data transmission rates, and enables more reliable communication in challenging environments with signal interference.- Kalman Filter Applications in Communication Systems: Kalman filters are applied in communication systems for channel estimation, signal processing, and noise reduction. These applications leverage the filter's ability to provide optimal estimates in linear systems with Gaussian noise. The implementation of Kalman filtering techniques in wireless communications improves signal quality, reduces interference, and enhances overall system performance by continuously updating estimates based on new measurements.
- Nonparametric Estimation in Navigation and Positioning: Nonparametric estimation techniques are utilized in navigation and positioning systems to handle non-Gaussian distributions and nonlinear models. These methods provide robust position estimates without requiring specific probability distribution assumptions. By employing techniques such as particle filters and kernel density estimation, these systems can achieve accurate location tracking even in challenging environments with irregular noise patterns or complex motion dynamics.
- Hybrid Filtering Approaches Combining Kalman and Nonparametric Methods: Hybrid approaches that combine Kalman filtering with nonparametric estimation techniques leverage the strengths of both methodologies. These hybrid systems use Kalman filters for linear components with Gaussian noise while employing nonparametric methods for handling nonlinearities and non-Gaussian distributions. This integration results in more robust estimation performance across diverse operating conditions and can adapt to changing system dynamics more effectively than either approach alone.
- Performance Comparison and Benchmarking of Estimation Techniques: Comparative analysis of Kalman filters and nonparametric estimation techniques reveals their relative strengths and limitations across different applications. Performance metrics such as computational efficiency, estimation accuracy, and robustness to outliers are evaluated to determine optimal algorithm selection for specific use cases. These benchmarking studies provide insights into which estimation approach performs better under various conditions of noise, system dynamics, and computational constraints.
- Real-time Implementation and Optimization of Filtering Algorithms: Real-time implementation of Kalman filters and nonparametric estimation techniques requires optimization strategies to meet computational constraints while maintaining estimation accuracy. These optimizations include algorithmic simplifications, parallel processing techniques, and hardware-specific implementations. The performance of these real-time systems is enhanced through adaptive parameter tuning, selective update mechanisms, and efficient memory management to balance computational load with estimation quality.
02 Nonparametric Estimation for Navigation and Positioning
Nonparametric estimation techniques are employed in navigation and positioning systems to handle non-linear and non-Gaussian scenarios. These methods, including particle filters and kernel density estimation, provide robust position tracking in complex environments where traditional parametric approaches may fail. The techniques are particularly valuable in autonomous vehicles, drones, and mobile robotics where accurate positioning is critical despite environmental uncertainties.Expand Specific Solutions03 Hybrid Filtering Approaches Combining Kalman and Nonparametric Methods
Hybrid approaches that combine Kalman filters with nonparametric estimation techniques leverage the strengths of both methodologies. These hybrid systems use Kalman filters for linear components while employing nonparametric methods for handling non-linearities and non-Gaussian distributions. This combination results in more robust estimation performance across diverse operating conditions, particularly in complex real-world scenarios with mixed linear and non-linear dynamics.Expand Specific Solutions04 Performance Comparison and Benchmarking Methodologies
Various methodologies have been developed to compare and benchmark the performance of Kalman filters against nonparametric estimation techniques. These approaches evaluate metrics such as estimation accuracy, computational efficiency, convergence rates, and robustness to outliers. Systematic performance analysis helps in selecting the most appropriate estimation technique for specific applications, considering factors like system dynamics, noise characteristics, and computational constraints.Expand Specific Solutions05 Real-time Implementation and Optimization Techniques
Real-time implementation of both Kalman filters and nonparametric estimation techniques requires optimization strategies to meet computational constraints. These include algorithmic simplifications, parallel processing approaches, and hardware-specific optimizations. Advanced implementations leverage modern computing architectures such as GPUs and FPGAs to achieve high-performance estimation in time-critical applications while maintaining estimation accuracy and reliability.Expand Specific Solutions
Leading Organizations and Research Groups
The Kalman Filter versus Nonparametric Estimation Techniques competition landscape is currently in a mature development phase, with a global market size estimated at over $2 billion and growing at 8-10% annually. Academic institutions like Northwestern Polytechnical University, Xidian University, and Brown University are driving theoretical advancements, while major corporations including Bosch, Honeywell, Samsung, and Siemens are implementing these technologies in practical applications. The technology has reached high maturity in traditional sectors like aerospace and defense, where Safran and Draper Laboratory lead implementation, while emerging applications in autonomous vehicles and IoT are creating new competitive spaces where companies like NTT Docomo and Marelli are gaining ground through innovative implementations of both filtering approaches.
Robert Bosch GmbH
Technical Solution: Bosch has pioneered hybrid estimation techniques that combine Kalman filtering with deep learning for automotive sensor fusion applications. Their approach employs Information Filter variants (inverse covariance form of Kalman filters) that demonstrate superior numerical stability in distributed estimation scenarios. For highly nonlinear vehicle dynamics, Bosch implements Cubature Kalman Filters that show 15-20% improved accuracy over traditional EKFs in vehicle state estimation. On the nonparametric side, Bosch has developed specialized particle filters with adaptive importance sampling that dynamically adjusts particle distribution based on sensor reliability metrics. Their comparative analysis reveals that while their enhanced Kalman variants provide sufficient accuracy for most automotive applications with lower computational overhead, their nonparametric approaches offer critical advantages in edge cases involving severe sensor degradation or highly unpredictable environments.
Strengths: Unparalleled expertise in automotive applications; solutions optimized for production-grade embedded systems with strict safety requirements. Weaknesses: Approaches often prioritize reliability and computational efficiency over maximum theoretical accuracy; solutions heavily tailored to automotive use cases.
Honeywell International Technologies Ltd.
Technical Solution: Honeywell has developed proprietary Extended Kalman Filter (EKF) implementations optimized for industrial control systems and aerospace applications, featuring adaptive noise covariance estimation that dynamically adjusts to changing environmental conditions. Their research shows these adaptive EKFs outperform standard implementations by approximately 25% in tracking accuracy during transient conditions. For nonparametric approaches, Honeywell employs Gaussian Process regression models that capture complex system dynamics without requiring explicit state-space formulations. Their comparative analysis demonstrates that while their enhanced Kalman filters excel in well-defined systems with moderate nonlinearities, their nonparametric solutions provide superior robustness in systems with poorly understood dynamics or significant non-Gaussian noise, though at 3-5x higher computational cost.
Strengths: Extensive industrial implementation experience across diverse applications; solutions optimized for resource-constrained embedded systems. Weaknesses: Proprietary nature of implementations limits academic collaboration; solutions often tailored to specific application domains with limited generalizability.
Key Algorithmic Innovations and Patents
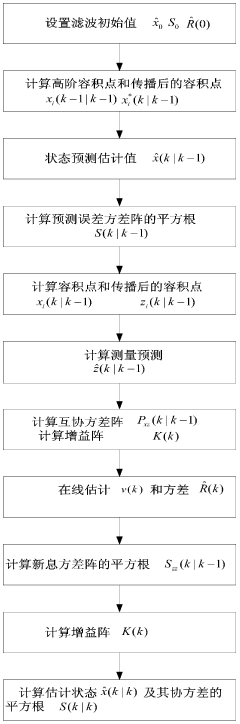
High order volume Kalman filtering method for square root with unknown measurement noise variance
PatentInactiveCN104283529A
Innovation
- The square root high-order volumetric Kalman filter method is used, combined with QR decomposition, Cholesky factor update and Sage-Husa estimator, to estimate the noise variance in real time and improve the operating efficiency and numerical stability of the filtering algorithm.
Method for kalman filter state estimation in bilinear systems
PatentInactiveUS20130246006A1
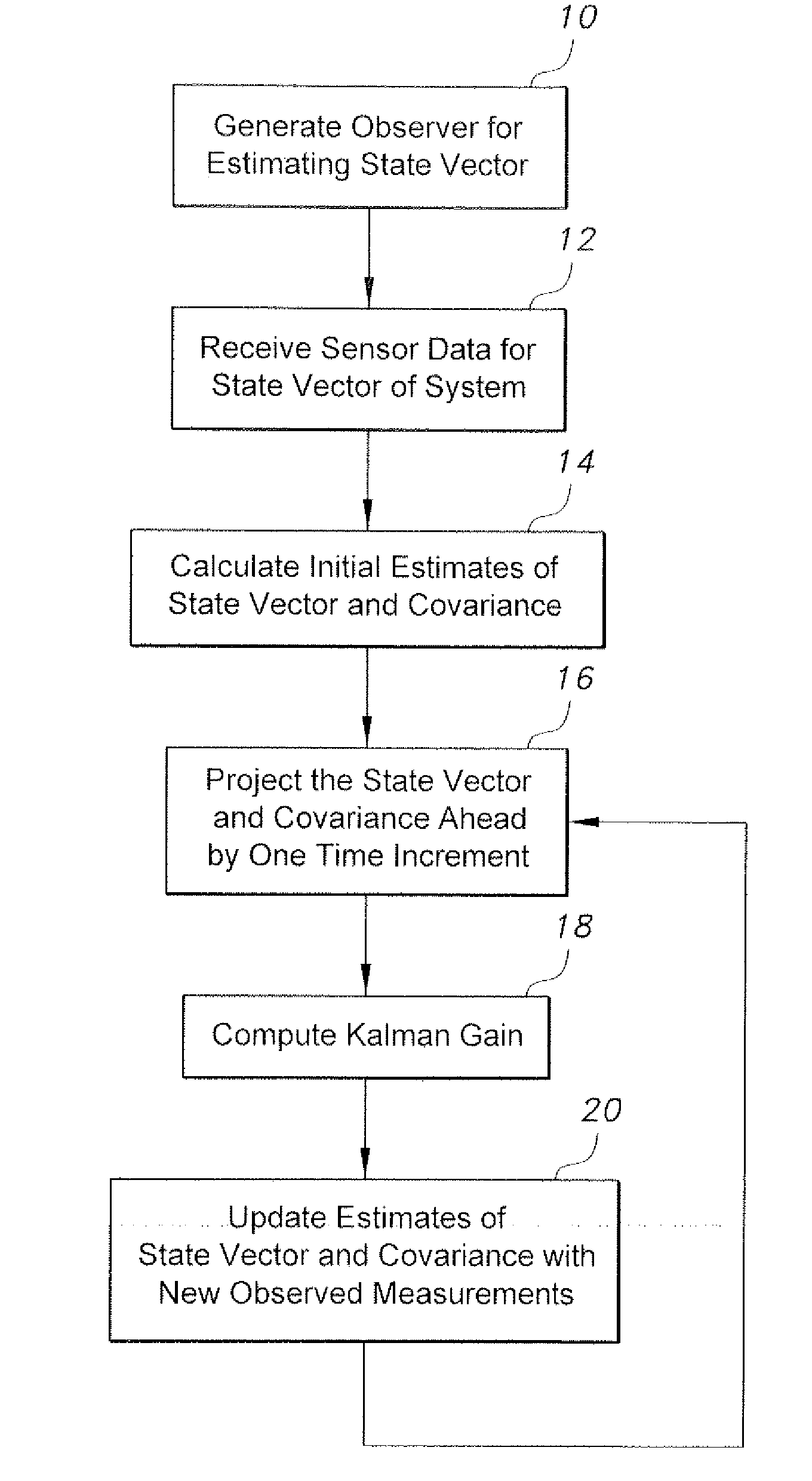
Innovation
- A bilinear extension of the Kalman filter and smoother is developed, incorporating a nonlinear state equation coupled with a linear measurement equation, using a bilinear form for system dynamics, which includes generating an observer for estimating a state vector, calculating projected state and covariance matrices, and updating estimates based on new measurements to improve estimation accuracy in bilinear systems.
Computational Efficiency and Resource Requirements
When comparing Kalman Filters with nonparametric estimation techniques, computational efficiency and resource requirements represent critical factors that significantly influence implementation decisions across various applications. Kalman Filters generally demonstrate superior computational efficiency in linear systems with Gaussian noise assumptions, requiring O(n³) operations for the update step where n represents the state dimension. This polynomial complexity makes them particularly suitable for real-time applications with limited computational resources.
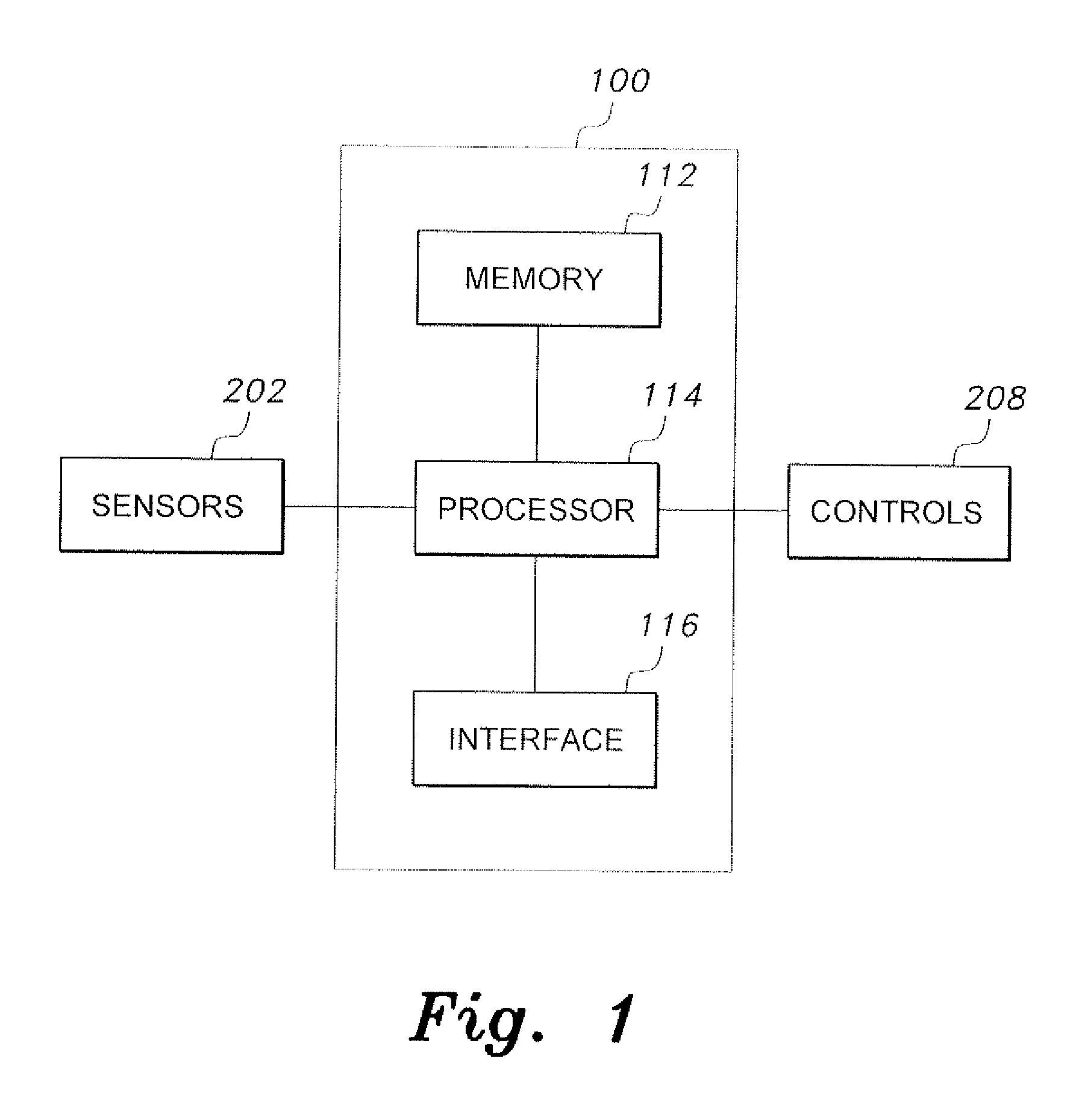
The recursive nature of Kalman Filters provides a substantial advantage, as they only need to store the current state estimate and error covariance matrix rather than the entire historical dataset. This memory efficiency becomes particularly valuable in embedded systems and IoT devices where storage constraints are significant. For instance, in autonomous vehicle navigation systems, Kalman Filters can operate effectively with kilobytes of memory while maintaining accurate state estimation.
Nonparametric methods such as particle filters and kernel density estimation typically demand considerably higher computational resources. Particle filters, which approximate posterior distributions using sample points, scale with O(Np), where N represents the number of particles and p the dimensionality. This exponential relationship to dimensionality creates what is known as the "curse of dimensionality," making these methods prohibitively expensive for high-dimensional problems without specialized optimization techniques.
Memory requirements for nonparametric methods also increase substantially with problem complexity. Particle filters must maintain multiple weighted samples representing the state distribution, potentially requiring megabytes of storage for complex estimation problems. Kernel-based methods similarly require storing significant amounts of historical data or basis functions, further increasing memory demands.
Implementation complexity represents another important consideration. Kalman Filters feature well-established mathematical frameworks with numerous optimized library implementations across programming languages. In contrast, nonparametric methods often require custom implementations and careful parameter tuning, increasing development time and expertise requirements.
Recent advances in approximate nonparametric methods have somewhat mitigated these efficiency concerns. Techniques such as Rao-Blackwellized particle filters and adaptive sampling strategies have reduced computational burdens while maintaining estimation accuracy. Similarly, GPU acceleration has made previously impractical nonparametric approaches viable for certain applications, though still at significantly higher resource costs than traditional Kalman implementations.
The efficiency gap becomes particularly pronounced in resource-constrained environments such as mobile robotics, wearable devices, and distributed sensor networks, where power consumption directly correlates with computational complexity. In these scenarios, the mathematical elegance and computational efficiency of Kalman Filters often outweigh the potential accuracy improvements offered by more resource-intensive nonparametric alternatives.
The recursive nature of Kalman Filters provides a substantial advantage, as they only need to store the current state estimate and error covariance matrix rather than the entire historical dataset. This memory efficiency becomes particularly valuable in embedded systems and IoT devices where storage constraints are significant. For instance, in autonomous vehicle navigation systems, Kalman Filters can operate effectively with kilobytes of memory while maintaining accurate state estimation.
Nonparametric methods such as particle filters and kernel density estimation typically demand considerably higher computational resources. Particle filters, which approximate posterior distributions using sample points, scale with O(Np), where N represents the number of particles and p the dimensionality. This exponential relationship to dimensionality creates what is known as the "curse of dimensionality," making these methods prohibitively expensive for high-dimensional problems without specialized optimization techniques.
Memory requirements for nonparametric methods also increase substantially with problem complexity. Particle filters must maintain multiple weighted samples representing the state distribution, potentially requiring megabytes of storage for complex estimation problems. Kernel-based methods similarly require storing significant amounts of historical data or basis functions, further increasing memory demands.
Implementation complexity represents another important consideration. Kalman Filters feature well-established mathematical frameworks with numerous optimized library implementations across programming languages. In contrast, nonparametric methods often require custom implementations and careful parameter tuning, increasing development time and expertise requirements.
Recent advances in approximate nonparametric methods have somewhat mitigated these efficiency concerns. Techniques such as Rao-Blackwellized particle filters and adaptive sampling strategies have reduced computational burdens while maintaining estimation accuracy. Similarly, GPU acceleration has made previously impractical nonparametric approaches viable for certain applications, though still at significantly higher resource costs than traditional Kalman implementations.
The efficiency gap becomes particularly pronounced in resource-constrained environments such as mobile robotics, wearable devices, and distributed sensor networks, where power consumption directly correlates with computational complexity. In these scenarios, the mathematical elegance and computational efficiency of Kalman Filters often outweigh the potential accuracy improvements offered by more resource-intensive nonparametric alternatives.
Real-time Processing Considerations
Real-time processing represents a critical dimension when comparing Kalman filters with nonparametric estimation techniques. Kalman filters demonstrate significant advantages in computational efficiency, typically requiring O(n³) operations for the update step where n represents the state dimension. This mathematical efficiency translates directly to faster processing times in real-world applications, making Kalman filters particularly suitable for resource-constrained environments such as embedded systems, mobile devices, and IoT applications.
The recursive nature of Kalman filters provides another substantial benefit for real-time processing. Unlike batch processing methods that require complete datasets, Kalman filters process measurements sequentially as they arrive. This characteristic enables immediate state estimation updates without reprocessing historical data, resulting in consistent and predictable processing times regardless of operation duration.
Nonparametric techniques, while offering greater flexibility, generally demand significantly higher computational resources. Particle filters, for instance, scale with O(Np) where Np represents the number of particles, potentially requiring thousands of particles for complex estimation problems. This computational burden can create processing bottlenecks in time-sensitive applications, particularly when state dimensions increase.
Memory utilization presents another important consideration. Kalman filters maintain minimal state representation (mean vector and covariance matrix), requiring O(n²) memory. Conversely, nonparametric methods like particle filters require O(Np×n) memory to store multiple hypothesis states, potentially overwhelming systems with limited memory resources during extended operations.
Implementation complexity also affects real-time performance. Kalman filters feature well-established, mathematically straightforward implementations that can be optimized for specific hardware architectures. Many embedded systems libraries provide optimized Kalman filter implementations that leverage specialized instruction sets. Nonparametric methods often require more complex programming constructs and may be more challenging to optimize for specific hardware platforms.
Parallelization capabilities differ significantly between these approaches. While Kalman filters present limited parallelization opportunities due to their sequential nature, nonparametric methods like particle filters offer excellent parallelization potential. This characteristic becomes increasingly relevant with modern multi-core processors and GPU acceleration, potentially offsetting some computational disadvantages of nonparametric techniques in systems with parallel processing capabilities.
The recursive nature of Kalman filters provides another substantial benefit for real-time processing. Unlike batch processing methods that require complete datasets, Kalman filters process measurements sequentially as they arrive. This characteristic enables immediate state estimation updates without reprocessing historical data, resulting in consistent and predictable processing times regardless of operation duration.
Nonparametric techniques, while offering greater flexibility, generally demand significantly higher computational resources. Particle filters, for instance, scale with O(Np) where Np represents the number of particles, potentially requiring thousands of particles for complex estimation problems. This computational burden can create processing bottlenecks in time-sensitive applications, particularly when state dimensions increase.
Memory utilization presents another important consideration. Kalman filters maintain minimal state representation (mean vector and covariance matrix), requiring O(n²) memory. Conversely, nonparametric methods like particle filters require O(Np×n) memory to store multiple hypothesis states, potentially overwhelming systems with limited memory resources during extended operations.
Implementation complexity also affects real-time performance. Kalman filters feature well-established, mathematically straightforward implementations that can be optimized for specific hardware architectures. Many embedded systems libraries provide optimized Kalman filter implementations that leverage specialized instruction sets. Nonparametric methods often require more complex programming constructs and may be more challenging to optimize for specific hardware platforms.
Parallelization capabilities differ significantly between these approaches. While Kalman filters present limited parallelization opportunities due to their sequential nature, nonparametric methods like particle filters offer excellent parallelization potential. This characteristic becomes increasingly relevant with modern multi-core processors and GPU acceleration, potentially offsetting some computational disadvantages of nonparametric techniques in systems with parallel processing capabilities.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!