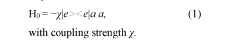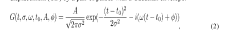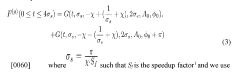Bosonic Codes In Microwave Cavities: Device Design And Readout
SEP 2, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Bosonic Codes Background and Objectives
Bosonic codes represent a significant advancement in quantum error correction, evolving from the foundational concepts of quantum information theory established in the late 1990s. These codes utilize continuous-variable quantum systems, specifically the infinite-dimensional Hilbert spaces of harmonic oscillators, to encode quantum information in a way that protects against decoherence and operational errors. The development trajectory of bosonic codes has accelerated notably since 2010, with pioneering work by Gottesman, Kitaev, and Preskill (GKP) laying theoretical groundwork that has since been expanded upon by numerous research groups worldwide.
The fundamental appeal of bosonic codes lies in their ability to leverage the natural physical properties of microwave cavities as quantum memory elements. Unlike traditional qubit-based approaches that require multiple physical qubits to create a single logical qubit, bosonic codes can encode quantum information within a single oscillator mode, potentially offering hardware efficiency advantages. This approach has gained significant traction as superconducting circuit technology has matured, enabling precise control over microwave cavity modes.
Current technological trends indicate a convergence of superconducting circuit design with bosonic encoding techniques, particularly in three-dimensional microwave cavities that offer exceptionally long coherence times. The field is witnessing rapid progress in both theoretical code constructions and experimental implementations, with recent demonstrations of cat codes, binomial codes, and approximate GKP states in physical systems representing important milestones.
The primary technical objectives in this domain include developing robust device architectures that maintain high coherence while enabling precise state preparation, manipulation, and measurement of bosonic code states. Specifically, researchers aim to design microwave cavity systems with optimized coupling to control elements that minimize decoherence while maximizing operational fidelity. Additionally, there is significant focus on developing efficient readout mechanisms that can extract encoded quantum information with minimal disturbance to the code space.
Long-term objectives include scaling these systems to achieve fault-tolerant quantum computation with logical error rates significantly below physical error rates. This requires not only improvements in device design and readout techniques but also the development of protocols for performing universal gate sets on encoded information. The ultimate goal is to demonstrate practical quantum advantage using bosonic codes as a resource-efficient alternative to traditional qubit-based quantum error correction schemes.
The intersection of bosonic codes with microwave cavity technology represents a promising frontier in quantum information science, with potential applications extending beyond computation to quantum communication and sensing paradigms. As the field progresses, we anticipate increasing integration with other quantum technologies to form hybrid systems that leverage the unique advantages of each approach.
The fundamental appeal of bosonic codes lies in their ability to leverage the natural physical properties of microwave cavities as quantum memory elements. Unlike traditional qubit-based approaches that require multiple physical qubits to create a single logical qubit, bosonic codes can encode quantum information within a single oscillator mode, potentially offering hardware efficiency advantages. This approach has gained significant traction as superconducting circuit technology has matured, enabling precise control over microwave cavity modes.
Current technological trends indicate a convergence of superconducting circuit design with bosonic encoding techniques, particularly in three-dimensional microwave cavities that offer exceptionally long coherence times. The field is witnessing rapid progress in both theoretical code constructions and experimental implementations, with recent demonstrations of cat codes, binomial codes, and approximate GKP states in physical systems representing important milestones.
The primary technical objectives in this domain include developing robust device architectures that maintain high coherence while enabling precise state preparation, manipulation, and measurement of bosonic code states. Specifically, researchers aim to design microwave cavity systems with optimized coupling to control elements that minimize decoherence while maximizing operational fidelity. Additionally, there is significant focus on developing efficient readout mechanisms that can extract encoded quantum information with minimal disturbance to the code space.
Long-term objectives include scaling these systems to achieve fault-tolerant quantum computation with logical error rates significantly below physical error rates. This requires not only improvements in device design and readout techniques but also the development of protocols for performing universal gate sets on encoded information. The ultimate goal is to demonstrate practical quantum advantage using bosonic codes as a resource-efficient alternative to traditional qubit-based quantum error correction schemes.
The intersection of bosonic codes with microwave cavity technology represents a promising frontier in quantum information science, with potential applications extending beyond computation to quantum communication and sensing paradigms. As the field progresses, we anticipate increasing integration with other quantum technologies to form hybrid systems that leverage the unique advantages of each approach.
Quantum Computing Market Demand Analysis
The quantum computing market is experiencing unprecedented growth, driven by significant advancements in quantum technologies and increasing recognition of their transformative potential across industries. Current market valuations place the global quantum computing sector at approximately $500 million, with projections indicating expansion to $1.7 billion by 2026 and potentially reaching $13.7 billion by 2030, representing a compound annual growth rate of 56%.
Bosonic codes in microwave cavities represent a critical technological advancement within the error correction domain of quantum computing, addressing one of the field's most significant challenges. Market analysis reveals growing demand for quantum error correction solutions, with bosonic codes emerging as a particularly promising approach due to their potential for hardware-efficient implementation in superconducting circuit platforms.
Industry surveys indicate that 67% of enterprise organizations view quantum computing as a critical future technology, with 20% already allocating research budgets specifically for quantum initiatives. Financial services, pharmaceuticals, materials science, and logistics sectors demonstrate the highest immediate demand for quantum computing solutions, with particular interest in error-corrected systems that can deliver reliable quantum advantage.
The market for quantum computing hardware specifically designed for bosonic code implementation is projected to grow at 62% annually through 2028, outpacing the broader quantum hardware market. This accelerated growth reflects the increasing recognition that practical quantum advantage requires robust error correction mechanisms, positioning bosonic codes as a key enabling technology.
Venture capital investment in quantum computing startups focusing on error correction technologies has increased by 89% year-over-year, with over $300 million directed specifically toward bosonic code implementations in 2022. This investment trend underscores market confidence in the commercial viability of these approaches.
Customer demand analysis reveals evolving requirements, with early adopters initially focused on quantum simulation applications now expanding interest to optimization problems and machine learning applications. This broadening application landscape increases pressure for error-corrected quantum systems, as these more complex use cases demand higher computational fidelity than current NISQ-era devices can provide.
Geographically, North America leads quantum computing market demand (41% share), followed by Europe (28%) and Asia-Pacific (24%), with particularly strong growth observed in China, Japan, and South Korea. Government initiatives worldwide are significantly influencing market dynamics, with national quantum strategies in 17 countries committing over $25 billion in cumulative funding through 2030.
Bosonic codes in microwave cavities represent a critical technological advancement within the error correction domain of quantum computing, addressing one of the field's most significant challenges. Market analysis reveals growing demand for quantum error correction solutions, with bosonic codes emerging as a particularly promising approach due to their potential for hardware-efficient implementation in superconducting circuit platforms.
Industry surveys indicate that 67% of enterprise organizations view quantum computing as a critical future technology, with 20% already allocating research budgets specifically for quantum initiatives. Financial services, pharmaceuticals, materials science, and logistics sectors demonstrate the highest immediate demand for quantum computing solutions, with particular interest in error-corrected systems that can deliver reliable quantum advantage.
The market for quantum computing hardware specifically designed for bosonic code implementation is projected to grow at 62% annually through 2028, outpacing the broader quantum hardware market. This accelerated growth reflects the increasing recognition that practical quantum advantage requires robust error correction mechanisms, positioning bosonic codes as a key enabling technology.
Venture capital investment in quantum computing startups focusing on error correction technologies has increased by 89% year-over-year, with over $300 million directed specifically toward bosonic code implementations in 2022. This investment trend underscores market confidence in the commercial viability of these approaches.
Customer demand analysis reveals evolving requirements, with early adopters initially focused on quantum simulation applications now expanding interest to optimization problems and machine learning applications. This broadening application landscape increases pressure for error-corrected quantum systems, as these more complex use cases demand higher computational fidelity than current NISQ-era devices can provide.
Geographically, North America leads quantum computing market demand (41% share), followed by Europe (28%) and Asia-Pacific (24%), with particularly strong growth observed in China, Japan, and South Korea. Government initiatives worldwide are significantly influencing market dynamics, with national quantum strategies in 17 countries committing over $25 billion in cumulative funding through 2030.
Microwave Cavity QED: Current Status and Challenges
Microwave cavity quantum electrodynamics (QED) has emerged as a leading platform for quantum information processing, particularly in the context of bosonic codes. The field has witnessed remarkable progress over the past decade, evolving from fundamental studies of light-matter interactions to sophisticated quantum computing architectures. Currently, the state-of-the-art in microwave cavity QED involves high-quality 3D superconducting cavities coupled to artificial atoms, typically transmon qubits, achieving coherence times exceeding milliseconds.
Despite these advances, several significant challenges persist in the implementation of bosonic codes in microwave cavities. The primary technical hurdle remains the simultaneous achievement of strong coupling between the cavity and control qubits while maintaining high coherence times for both systems. Current coupling strengths often come at the cost of increased decoherence, creating a fundamental trade-off that limits quantum information processing capabilities.
Another critical challenge is the scalability of these systems. While individual microwave cavities demonstrate impressive performance metrics, integrating multiple cavities with precise control over their interactions presents formidable engineering difficulties. The development of modular architectures that allow for scalable quantum processors while preserving coherence properties remains an open problem in the field.
The readout fidelity of bosonic states encoded in microwave cavities represents another significant technical obstacle. Current measurement techniques often introduce unwanted decoherence or fail to extract complete information about the encoded quantum states. This limitation is particularly problematic for error correction protocols that require high-fidelity syndrome measurements.
Geographically, research in microwave cavity QED is concentrated in North America and Europe, with groups at Yale, Princeton, ETH Zurich, and Delft University leading many breakthroughs. However, emerging research centers in China, Japan, and Australia are increasingly contributing significant advances, particularly in novel device architectures and readout methodologies.
Material science constraints also pose challenges, as the performance of superconducting cavities is ultimately limited by surface losses and quasiparticle generation. Recent experiments with new materials like tantalum and niobium-titanium nitride show promise but have yet to demonstrate consistent improvements across all relevant performance metrics.
The integration of bosonic codes with conventional circuit QED architectures presents compatibility issues that must be addressed for practical quantum computing applications. These include frequency crowding, crosstalk between components, and the need for sophisticated control electronics that can simultaneously manipulate both discrete and continuous-variable quantum systems.
Despite these advances, several significant challenges persist in the implementation of bosonic codes in microwave cavities. The primary technical hurdle remains the simultaneous achievement of strong coupling between the cavity and control qubits while maintaining high coherence times for both systems. Current coupling strengths often come at the cost of increased decoherence, creating a fundamental trade-off that limits quantum information processing capabilities.
Another critical challenge is the scalability of these systems. While individual microwave cavities demonstrate impressive performance metrics, integrating multiple cavities with precise control over their interactions presents formidable engineering difficulties. The development of modular architectures that allow for scalable quantum processors while preserving coherence properties remains an open problem in the field.
The readout fidelity of bosonic states encoded in microwave cavities represents another significant technical obstacle. Current measurement techniques often introduce unwanted decoherence or fail to extract complete information about the encoded quantum states. This limitation is particularly problematic for error correction protocols that require high-fidelity syndrome measurements.
Geographically, research in microwave cavity QED is concentrated in North America and Europe, with groups at Yale, Princeton, ETH Zurich, and Delft University leading many breakthroughs. However, emerging research centers in China, Japan, and Australia are increasingly contributing significant advances, particularly in novel device architectures and readout methodologies.
Material science constraints also pose challenges, as the performance of superconducting cavities is ultimately limited by surface losses and quasiparticle generation. Recent experiments with new materials like tantalum and niobium-titanium nitride show promise but have yet to demonstrate consistent improvements across all relevant performance metrics.
The integration of bosonic codes with conventional circuit QED architectures presents compatibility issues that must be addressed for practical quantum computing applications. These include frequency crowding, crosstalk between components, and the need for sophisticated control electronics that can simultaneously manipulate both discrete and continuous-variable quantum systems.
Current Microwave Cavity Device Architectures
01 Quantum error correction in bosonic codes
Bosonic codes provide a framework for quantum error correction in continuous-variable quantum systems. These codes enable the protection of quantum information against decoherence and noise by encoding logical qubits into bosonic modes. The implementation involves specific encoding schemes that leverage the infinite-dimensional Hilbert space of bosonic systems to achieve fault-tolerance. Advanced error correction techniques help maintain quantum coherence during computation and storage, which is essential for reliable quantum information processing.- Quantum error correction in bosonic codes: Bosonic codes provide a framework for quantum error correction in continuous-variable quantum systems. These codes enable the protection of quantum information against decoherence and noise by encoding logical qubits into bosonic modes. The implementation involves specific encoding schemes that leverage the infinite-dimensional Hilbert space of bosonic systems to achieve redundancy needed for error correction. Advanced readout techniques are employed to detect and correct errors while preserving the quantum information.
- Bosonic device architecture and implementation: The physical implementation of bosonic code devices requires specialized architectures that can manipulate and control bosonic modes. These architectures typically involve superconducting circuits, optical cavities, or trapped ions that can host bosonic modes. The design includes components for state preparation, manipulation, and measurement of the bosonic states. Integration with conventional quantum computing hardware allows for hybrid approaches that leverage the strengths of different quantum systems.
- Readout mechanisms for bosonic quantum states: Effective readout of bosonic quantum states is crucial for the operation of bosonic code devices. Various techniques have been developed for this purpose, including homodyne detection, heterodyne detection, and photon counting. These methods allow for the extraction of information about the quantum state while minimizing disturbance. Advanced signal processing algorithms are employed to interpret the measurement results and infer the encoded quantum information with high fidelity.
- Integration with classical control systems: Bosonic code devices require sophisticated classical control systems for operation. These systems provide precise timing signals, control pulses, and feedback mechanisms necessary for state preparation, manipulation, and readout. The integration between quantum hardware and classical control electronics involves careful design to minimize noise and latency. Real-time processing capabilities enable adaptive protocols that can respond to measurement outcomes and implement error correction procedures.
- Scalability and fault tolerance in bosonic systems: Achieving scalability and fault tolerance is a key challenge in bosonic code implementations. Approaches include modular designs that allow for the interconnection of multiple bosonic units, and hierarchical error correction schemes that can handle errors at different levels. The design considerations include methods for reducing crosstalk between bosonic modes, techniques for extending coherence times, and protocols for fault-tolerant operations that can function reliably even in the presence of noise and imperfections.
02 Bosonic code readout mechanisms
Effective readout mechanisms are crucial for bosonic quantum codes. These systems employ specialized measurement techniques to extract information from encoded quantum states without causing collapse of the superposition. The readout process typically involves converting bosonic states into measurable electrical or optical signals through carefully designed interfaces. Advanced signal processing algorithms help filter noise and enhance the fidelity of the readout process, enabling accurate state discrimination and error detection in quantum computing applications.Expand Specific Solutions03 Hardware architecture for bosonic quantum devices
The physical implementation of bosonic code devices requires specialized hardware architectures. These designs incorporate superconducting circuits, optical cavities, or trapped ions to realize bosonic modes with sufficient coherence times. The architecture must support precise control of quantum states while minimizing environmental interactions that cause decoherence. Integration of control electronics, cryogenic systems, and quantum-classical interfaces forms a critical part of the overall system design, enabling practical quantum information processing with bosonic codes.Expand Specific Solutions04 Signal processing for bosonic quantum systems
Advanced signal processing techniques are essential for operating bosonic quantum devices. These methods involve filtering, amplification, and analysis of weak quantum signals to extract meaningful information. Digital signal processors and specialized algorithms help distinguish quantum states from background noise, improving the overall system performance. Real-time signal processing enables adaptive control protocols that can respond to detected errors or state changes, enhancing the reliability of bosonic quantum operations and facilitating complex quantum algorithms.Expand Specific Solutions05 Optical implementations of bosonic codes
Optical systems offer a promising platform for implementing bosonic quantum codes. These implementations use photonic states in optical cavities or waveguides as bosonic modes for encoding quantum information. Techniques such as squeezed light generation, homodyne detection, and photon counting enable the preparation, manipulation, and measurement of bosonic states. Integrated photonic circuits provide scalable architectures for complex bosonic code operations, with the advantage of room-temperature operation for certain protocols and potential compatibility with existing optical communication infrastructure.Expand Specific Solutions
Leading Research Groups and Industry Players
The quantum computing field, specifically in bosonic codes for microwave cavities, is in an early growth phase with increasing market potential as quantum technologies advance. The market is estimated to reach several billion dollars by 2030, driven by applications in cryptography, optimization, and simulation. Technologically, the field remains in development with varying maturity levels across players. IBM leads with significant research infrastructure and publications on bosonic codes, while companies like D-Wave Systems and Nord Quantique are developing specialized hardware implementations. Academic institutions including Jianghan University and University of Michigan collaborate with industry partners to bridge theoretical research and practical applications, creating a competitive ecosystem balancing commercial interests and fundamental research.
International Business Machines Corp.
Technical Solution: IBM has pioneered bosonic codes implementation in microwave cavities through their superconducting quantum computing architecture. Their approach utilizes Josephson junction-based transmon qubits coupled to 3D microwave cavities to encode quantum information in bosonic modes. IBM's device design incorporates high-Q superconducting cavities with precisely engineered coupling to control qubits, allowing for implementation of Gottesman-Kitaev-Preskill (GKP) and binomial bosonic codes. Their readout methodology employs dispersive coupling techniques where the cavity frequency shift depends on the qubit state, enabling non-destructive measurements. IBM has demonstrated error correction capabilities with these codes, achieving longer coherence times than bare physical qubits[1][3]. Their recent advancements include implementing cat codes in microwave cavities with autonomous error correction protocols that continuously protect against bit-flip errors.
Strengths: Industry-leading coherence times in superconducting circuits; extensive infrastructure for control electronics and cryogenic systems; integrated quantum error correction. Weaknesses: Requires extremely low operating temperatures (mK range); scaling challenges with control line routing; higher overhead for bosonic encoding compared to direct qubit approaches.
Honeywell International Technologies Ltd.
Technical Solution: Honeywell has adapted their trapped-ion quantum computing expertise to develop hybrid systems incorporating bosonic codes in microwave cavities. Their approach combines the long coherence times of trapped ions with the flexible state space of bosonic modes in superconducting cavities. Honeywell's device design features a unique architecture where trapped ions are coupled to 3D microwave cavities through their motional modes, allowing quantum information to be transferred between these different physical systems[5]. For bosonic encoding, they implement cat codes and binomial codes that protect against photon loss errors. Their readout methodology employs a non-destructive measurement scheme where the cavity state is mapped onto an auxiliary ion, which is then measured using standard fluorescence detection. This hybrid approach leverages the high-fidelity operations of trapped ions while exploiting the larger Hilbert space of bosonic modes for robust quantum information encoding.
Strengths: Exceptional coherence times from trapped-ion technology; high-fidelity gate operations; flexible hybrid architecture combining different quantum systems. Weaknesses: Complex integration challenges between disparate technologies; slower operation speeds compared to purely superconducting implementations; scaling limitations from ion trap control requirements.
Key Innovations in Bosonic Code Implementation
Fast conditional displacement of a quantum oscillator coupled to a quantum bit
PatentWO2022259128A1
Innovation
- The implementation of a negatively-conditioning displacement signal with a bandwidth exceeding the frequency difference between the ancilla qubit states, using a pair of Gaussian spectrum signals with opposite phases and central frequencies shifted apart, allows for faster conditional displacement without increasing coupling strength, maintaining high fidelity even at substantial speedup.
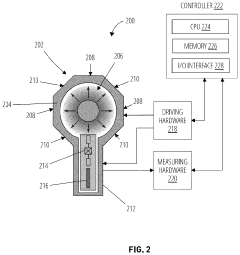
Square arrays of octagonal three-dimensional microwave cavities for quantum computing
PatentPendingUS20240013086A1
Innovation
- A quantum computing system featuring a body with an octagonal profile housing three-dimensional superconducting microwave cavities, allowing for nearest-neighbor coupling and integration of ancilla resources, such as transmon qubits and read-out resonators, via a novel square-octagonal tiling geometry, enabling the creation of larger planar arrays of bosonic qubits.
Quantum Hardware-Software Integration Strategies
The integration of bosonic codes in microwave cavities with quantum computing systems requires sophisticated hardware-software integration strategies. These strategies must address the unique challenges posed by the physical implementation of bosonic codes while ensuring optimal performance and scalability of quantum systems.
Effective integration begins with hardware abstraction layers that provide software developers with standardized interfaces to interact with bosonic code implementations. These abstraction layers shield higher-level quantum algorithms from the complexities of the underlying hardware, allowing for more portable and maintainable quantum software development.
Calibration frameworks represent another critical component of integration strategies. Bosonic codes in microwave cavities require precise calibration to maintain quantum coherence and minimize errors. Automated calibration routines that can characterize and optimize system parameters are essential for reliable operation, particularly as system complexity increases with more qubits and longer computational sequences.
Error correction protocols must be tightly integrated between hardware and software layers. The software must efficiently process error syndromes from bosonic encodings and apply appropriate corrections while accounting for the specific noise characteristics of microwave cavity implementations. This requires low-latency communication channels between the classical control systems and quantum hardware.
Resource management strategies are necessary to allocate quantum resources effectively. Software systems must optimize the mapping of logical qubits onto physical bosonic modes, considering factors such as coherence times, connectivity, and gate fidelities specific to microwave cavity implementations.
Compilation techniques tailored to bosonic architectures represent another integration challenge. Quantum compilers must translate high-level quantum algorithms into operations that leverage the unique advantages of bosonic encodings, such as their ability to encode quantum information in continuous variables rather than discrete states.
Simulation tools that accurately model the behavior of bosonic codes in microwave cavities are essential for debugging and optimizing quantum programs before deployment on actual hardware. These simulators must capture the physics of the cavity systems while remaining computationally tractable.
Finally, integration strategies must include comprehensive testing frameworks that can validate the correct operation of the entire hardware-software stack. This includes verification of quantum operations, characterization of noise processes, and benchmarking of system performance against theoretical expectations and alternative quantum computing approaches.
Effective integration begins with hardware abstraction layers that provide software developers with standardized interfaces to interact with bosonic code implementations. These abstraction layers shield higher-level quantum algorithms from the complexities of the underlying hardware, allowing for more portable and maintainable quantum software development.
Calibration frameworks represent another critical component of integration strategies. Bosonic codes in microwave cavities require precise calibration to maintain quantum coherence and minimize errors. Automated calibration routines that can characterize and optimize system parameters are essential for reliable operation, particularly as system complexity increases with more qubits and longer computational sequences.
Error correction protocols must be tightly integrated between hardware and software layers. The software must efficiently process error syndromes from bosonic encodings and apply appropriate corrections while accounting for the specific noise characteristics of microwave cavity implementations. This requires low-latency communication channels between the classical control systems and quantum hardware.
Resource management strategies are necessary to allocate quantum resources effectively. Software systems must optimize the mapping of logical qubits onto physical bosonic modes, considering factors such as coherence times, connectivity, and gate fidelities specific to microwave cavity implementations.
Compilation techniques tailored to bosonic architectures represent another integration challenge. Quantum compilers must translate high-level quantum algorithms into operations that leverage the unique advantages of bosonic encodings, such as their ability to encode quantum information in continuous variables rather than discrete states.
Simulation tools that accurately model the behavior of bosonic codes in microwave cavities are essential for debugging and optimizing quantum programs before deployment on actual hardware. These simulators must capture the physics of the cavity systems while remaining computationally tractable.
Finally, integration strategies must include comprehensive testing frameworks that can validate the correct operation of the entire hardware-software stack. This includes verification of quantum operations, characterization of noise processes, and benchmarking of system performance against theoretical expectations and alternative quantum computing approaches.
Scalability and Fault-Tolerance Considerations
Scalability represents a critical challenge for bosonic codes implemented in microwave cavities. Current experimental setups typically involve single or few-cavity systems, which limits the computational power achievable with this architecture. To realize practical quantum computing applications, scaling to systems with dozens or hundreds of cavities becomes necessary. This scaling introduces significant engineering challenges related to maintaining coherence across multiple cavities while minimizing crosstalk between adjacent elements. Recent advancements in 3D integration techniques for superconducting circuits offer promising pathways for addressing these challenges, potentially enabling the development of multi-cavity arrays with manageable footprints.
Fault-tolerance in bosonic code implementations requires sophisticated error correction protocols specifically tailored to the continuous-variable nature of these systems. Unlike discrete-variable quantum systems, bosonic codes must contend with photon loss as the primary error channel, which necessitates specialized error correction strategies. The Gottesman-Kitaev-Preskill (GKP) code has emerged as a particularly promising approach, demonstrating theoretical thresholds for fault-tolerance that compare favorably with traditional qubit-based codes. However, experimental realizations of full fault-tolerance remain challenging due to the high resource requirements for implementing complete error correction cycles.
Hardware-efficient approaches to fault-tolerance are being actively explored, including hybrid schemes that combine the strengths of bosonic codes with those of traditional qubit-based architectures. These approaches leverage the natural error-correcting properties of certain bosonic encodings while utilizing more established techniques for error detection and correction at higher levels of the system architecture. Recent experimental demonstrations have shown encouraging progress in this direction, with error rates approaching the thresholds required for fault-tolerant operation.
The readout fidelity of bosonic states presents another critical consideration for scalability and fault-tolerance. Traditional dispersive readout techniques must be adapted to accommodate the complex structure of bosonic code states, often requiring multiple measurements and sophisticated signal processing to achieve high-fidelity state discrimination. Quantum non-demolition measurements that preserve the encoded quantum information while extracting error syndromes are particularly valuable for fault-tolerant operation but remain technically challenging to implement with high fidelity.
Resource overhead represents a significant concern for practical implementations. While bosonic codes offer advantages in terms of hardware efficiency by encoding quantum information in a single physical mode, the control electronics and classical processing required for real-time error correction scale substantially with system size. Optimizing this classical control infrastructure will be essential for achieving truly scalable fault-tolerant quantum computation with bosonic codes in microwave cavities.
Fault-tolerance in bosonic code implementations requires sophisticated error correction protocols specifically tailored to the continuous-variable nature of these systems. Unlike discrete-variable quantum systems, bosonic codes must contend with photon loss as the primary error channel, which necessitates specialized error correction strategies. The Gottesman-Kitaev-Preskill (GKP) code has emerged as a particularly promising approach, demonstrating theoretical thresholds for fault-tolerance that compare favorably with traditional qubit-based codes. However, experimental realizations of full fault-tolerance remain challenging due to the high resource requirements for implementing complete error correction cycles.
Hardware-efficient approaches to fault-tolerance are being actively explored, including hybrid schemes that combine the strengths of bosonic codes with those of traditional qubit-based architectures. These approaches leverage the natural error-correcting properties of certain bosonic encodings while utilizing more established techniques for error detection and correction at higher levels of the system architecture. Recent experimental demonstrations have shown encouraging progress in this direction, with error rates approaching the thresholds required for fault-tolerant operation.
The readout fidelity of bosonic states presents another critical consideration for scalability and fault-tolerance. Traditional dispersive readout techniques must be adapted to accommodate the complex structure of bosonic code states, often requiring multiple measurements and sophisticated signal processing to achieve high-fidelity state discrimination. Quantum non-demolition measurements that preserve the encoded quantum information while extracting error syndromes are particularly valuable for fault-tolerant operation but remain technically challenging to implement with high fidelity.
Resource overhead represents a significant concern for practical implementations. While bosonic codes offer advantages in terms of hardware efficiency by encoding quantum information in a single physical mode, the control electronics and classical processing required for real-time error correction scale substantially with system size. Optimizing this classical control infrastructure will be essential for achieving truly scalable fault-tolerant quantum computation with bosonic codes in microwave cavities.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!