Finite Element Implementation Of Phase Transformation Kinetics In Materials
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Phase Transformation Kinetics Background and Objectives
Phase transformation kinetics in materials represents a fundamental area of materials science that has evolved significantly over the past century. The study of how materials transform from one phase to another under varying conditions of temperature, pressure, and composition has its roots in the pioneering work of Johnson, Mehl, Avrami, and Kolmogorov in the 1930s and 1940s, who developed mathematical frameworks to describe transformation processes. These early models have since been refined and expanded to accommodate increasingly complex material systems and transformation mechanisms.
The evolution of computational capabilities has revolutionized this field, transitioning from analytical solutions of simplified problems to sophisticated numerical simulations of realistic material behaviors. The finite element method (FEM), first developed in the 1950s for structural analysis, has emerged as a powerful tool for modeling phase transformations by discretizing complex geometries and solving the governing differential equations across these domains.
Current technological trends in this field include multi-scale modeling approaches that bridge atomic-level phenomena with macroscopic material behavior, integration of machine learning techniques to accelerate simulations, and development of coupled models that simultaneously account for mechanical, thermal, and chemical effects during phase transformations.
The primary objective of implementing phase transformation kinetics within finite element frameworks is to accurately predict microstructural evolution in materials under various processing and service conditions. This capability is crucial for designing materials with tailored properties and optimizing manufacturing processes across industries including aerospace, automotive, energy, and biomedical sectors.
Specific technical goals include developing robust numerical algorithms that can handle the inherent non-linearities and discontinuities associated with phase transformations, creating efficient computational methods that balance accuracy with reasonable computation times, and establishing validated models that can reliably predict transformation behavior in complex multi-component systems.
Additionally, there is growing emphasis on incorporating real-time feedback mechanisms that allow for adaptive control of material processing based on transformation kinetics, enabling more precise manufacturing outcomes. The ultimate aim is to establish a comprehensive digital framework that connects material composition, processing parameters, microstructural evolution, and final properties in a predictive manner, supporting accelerated materials development and process optimization.
The evolution of computational capabilities has revolutionized this field, transitioning from analytical solutions of simplified problems to sophisticated numerical simulations of realistic material behaviors. The finite element method (FEM), first developed in the 1950s for structural analysis, has emerged as a powerful tool for modeling phase transformations by discretizing complex geometries and solving the governing differential equations across these domains.
Current technological trends in this field include multi-scale modeling approaches that bridge atomic-level phenomena with macroscopic material behavior, integration of machine learning techniques to accelerate simulations, and development of coupled models that simultaneously account for mechanical, thermal, and chemical effects during phase transformations.
The primary objective of implementing phase transformation kinetics within finite element frameworks is to accurately predict microstructural evolution in materials under various processing and service conditions. This capability is crucial for designing materials with tailored properties and optimizing manufacturing processes across industries including aerospace, automotive, energy, and biomedical sectors.
Specific technical goals include developing robust numerical algorithms that can handle the inherent non-linearities and discontinuities associated with phase transformations, creating efficient computational methods that balance accuracy with reasonable computation times, and establishing validated models that can reliably predict transformation behavior in complex multi-component systems.
Additionally, there is growing emphasis on incorporating real-time feedback mechanisms that allow for adaptive control of material processing based on transformation kinetics, enabling more precise manufacturing outcomes. The ultimate aim is to establish a comprehensive digital framework that connects material composition, processing parameters, microstructural evolution, and final properties in a predictive manner, supporting accelerated materials development and process optimization.
Market Applications of Phase Transformation Simulation
Phase transformation simulation technologies have penetrated various high-value industrial sectors, creating substantial market opportunities. In aerospace engineering, these simulations enable the development of advanced alloys with precisely controlled microstructures for critical components in aircraft engines and structural elements. By accurately predicting phase transformations during manufacturing processes, aerospace manufacturers can optimize material properties such as fatigue resistance and thermal stability, directly contributing to improved safety margins and extended service life of components.
The automotive industry represents another significant market application, where phase transformation simulations facilitate the design of advanced high-strength steels and lightweight alloys. These materials are essential for meeting stringent fuel efficiency standards while maintaining crash safety requirements. Manufacturers utilize simulation capabilities to develop tailored microstructures through controlled heat treatment processes, resulting in components with optimized strength-to-weight ratios and improved formability characteristics.
In the energy sector, phase transformation simulations have become indispensable for developing materials used in extreme environments. Power generation equipment, particularly in nuclear and thermal power plants, requires materials that maintain structural integrity under high temperatures, pressures, and radiation exposure. Simulation tools enable engineers to predict long-term material behavior and degradation mechanisms, significantly reducing development cycles and validation costs.
The medical device industry has also embraced phase transformation simulation for developing biocompatible alloys with specific functional properties. Shape memory alloys used in stents, orthopedic implants, and surgical instruments rely on precisely controlled phase transformations. Simulation capabilities allow medical device manufacturers to design materials with optimal biocompatibility, mechanical properties, and functional response to physiological conditions.
Additive manufacturing represents an emerging market application with exceptional growth potential. The layer-by-layer building process involves complex thermal cycles that directly influence material microstructure and resultant properties. Phase transformation simulations enable manufacturers to predict and control these transformations, addressing challenges related to residual stress, dimensional accuracy, and mechanical performance of printed components.
Electronics manufacturing benefits from phase transformation simulations in the development of solder materials, interconnects, and packaging solutions. As electronic devices continue to miniaturize while increasing in functionality, the reliability of interconnections becomes increasingly critical. Simulation tools help predict failure mechanisms related to phase transformations during thermal cycling, supporting the development of more reliable electronic assemblies.
The automotive industry represents another significant market application, where phase transformation simulations facilitate the design of advanced high-strength steels and lightweight alloys. These materials are essential for meeting stringent fuel efficiency standards while maintaining crash safety requirements. Manufacturers utilize simulation capabilities to develop tailored microstructures through controlled heat treatment processes, resulting in components with optimized strength-to-weight ratios and improved formability characteristics.
In the energy sector, phase transformation simulations have become indispensable for developing materials used in extreme environments. Power generation equipment, particularly in nuclear and thermal power plants, requires materials that maintain structural integrity under high temperatures, pressures, and radiation exposure. Simulation tools enable engineers to predict long-term material behavior and degradation mechanisms, significantly reducing development cycles and validation costs.
The medical device industry has also embraced phase transformation simulation for developing biocompatible alloys with specific functional properties. Shape memory alloys used in stents, orthopedic implants, and surgical instruments rely on precisely controlled phase transformations. Simulation capabilities allow medical device manufacturers to design materials with optimal biocompatibility, mechanical properties, and functional response to physiological conditions.
Additive manufacturing represents an emerging market application with exceptional growth potential. The layer-by-layer building process involves complex thermal cycles that directly influence material microstructure and resultant properties. Phase transformation simulations enable manufacturers to predict and control these transformations, addressing challenges related to residual stress, dimensional accuracy, and mechanical performance of printed components.
Electronics manufacturing benefits from phase transformation simulations in the development of solder materials, interconnects, and packaging solutions. As electronic devices continue to miniaturize while increasing in functionality, the reliability of interconnections becomes increasingly critical. Simulation tools help predict failure mechanisms related to phase transformations during thermal cycling, supporting the development of more reliable electronic assemblies.
Current FEA Implementation Challenges
The implementation of phase transformation kinetics in finite element analysis (FEA) faces several significant challenges that limit the accuracy and applicability of current models. One of the primary difficulties lies in the multi-scale nature of phase transformations, which occur at the microstructural level but manifest effects at the macroscopic scale. This creates a fundamental computational challenge as simulations must bridge these disparate length scales while maintaining reasonable computational efficiency.
Constitutive modeling presents another major hurdle, as the material behavior during phase transformation involves complex thermomechanical coupling. Current FEA implementations struggle to accurately represent the simultaneous evolution of microstructure, temperature fields, and mechanical responses. The non-linear nature of these interactions often leads to convergence issues in numerical solutions, particularly when sharp transformation fronts are present.
Mesh dependency remains a persistent problem in phase transformation simulations. The discrete nature of finite element meshes can artificially influence transformation pathways, especially when the transformation involves volume changes or interface movements. Adaptive meshing techniques have been proposed as solutions but introduce additional computational complexity and may still fail to capture rapid transformation kinetics accurately.
Time-stepping algorithms face particular challenges when dealing with phase transformations that occur across vastly different time scales. Rapid transformations like martensitic transitions may require extremely small time steps for stability, while slower diffusion-controlled transformations need extended simulation periods. Current implementations often compromise between accuracy and computational feasibility, leading to potential errors in transformation prediction.
The treatment of transformation-induced plasticity (TRIP) and other complex mechanical phenomena associated with phase changes remains inadequately addressed in many FEA implementations. These effects significantly influence the stress-strain response of materials but are frequently oversimplified or omitted entirely due to implementation difficulties.
Data availability for model calibration represents another significant challenge. Accurate phase transformation models require extensive experimental data across various loading conditions and temperature regimes. The scarcity of comprehensive datasets forces many implementations to rely on simplified assumptions or extrapolations beyond their validated ranges.
Computational efficiency concerns continue to limit the practical application of phase transformation models in industrial settings. Full-scale simulations incorporating detailed transformation kinetics often require prohibitive computational resources, leading to simplified approaches that sacrifice accuracy for tractability in real-world engineering applications.
Constitutive modeling presents another major hurdle, as the material behavior during phase transformation involves complex thermomechanical coupling. Current FEA implementations struggle to accurately represent the simultaneous evolution of microstructure, temperature fields, and mechanical responses. The non-linear nature of these interactions often leads to convergence issues in numerical solutions, particularly when sharp transformation fronts are present.
Mesh dependency remains a persistent problem in phase transformation simulations. The discrete nature of finite element meshes can artificially influence transformation pathways, especially when the transformation involves volume changes or interface movements. Adaptive meshing techniques have been proposed as solutions but introduce additional computational complexity and may still fail to capture rapid transformation kinetics accurately.
Time-stepping algorithms face particular challenges when dealing with phase transformations that occur across vastly different time scales. Rapid transformations like martensitic transitions may require extremely small time steps for stability, while slower diffusion-controlled transformations need extended simulation periods. Current implementations often compromise between accuracy and computational feasibility, leading to potential errors in transformation prediction.
The treatment of transformation-induced plasticity (TRIP) and other complex mechanical phenomena associated with phase changes remains inadequately addressed in many FEA implementations. These effects significantly influence the stress-strain response of materials but are frequently oversimplified or omitted entirely due to implementation difficulties.
Data availability for model calibration represents another significant challenge. Accurate phase transformation models require extensive experimental data across various loading conditions and temperature regimes. The scarcity of comprehensive datasets forces many implementations to rely on simplified assumptions or extrapolations beyond their validated ranges.
Computational efficiency concerns continue to limit the practical application of phase transformation models in industrial settings. Full-scale simulations incorporating detailed transformation kinetics often require prohibitive computational resources, leading to simplified approaches that sacrifice accuracy for tractability in real-world engineering applications.
State-of-the-Art FEA Solutions for Phase Transformations
01 Measurement and analysis of phase transformation kinetics
Various methods and devices are used to measure and analyze phase transformation kinetics in materials. These include specialized equipment for monitoring phase changes, analytical techniques for determining transformation rates, and computational models that predict transformation behavior. These approaches enable researchers to understand the fundamental mechanisms of phase transformations and develop materials with controlled microstructures.- Measurement and analysis of phase transformation kinetics: Various methods and devices are used to measure and analyze phase transformation kinetics in materials. These include specialized equipment for monitoring changes in material properties during phase transitions, computational models for predicting transformation behavior, and analytical techniques for characterizing transformation mechanisms. These approaches enable researchers to understand the fundamental processes governing how materials transform from one phase to another under different conditions.
- Control systems for phase transformation processes: Advanced control systems are implemented to manage and optimize phase transformation processes in materials. These systems utilize sensors, feedback mechanisms, and automated controls to maintain precise conditions necessary for desired phase transformations. By carefully regulating parameters such as temperature, pressure, and composition, these control systems enable consistent and reproducible material transformations in industrial applications.
- Novel materials with engineered phase transformation properties: Development of new materials with specifically engineered phase transformation characteristics for various applications. These materials are designed to undergo controlled phase changes in response to external stimuli such as temperature, stress, or electromagnetic fields. The engineered transformation properties enable functional behaviors like shape memory effects, superelasticity, or enhanced mechanical performance under specific operating conditions.
- Simulation and modeling of phase transformation kinetics: Computational methods and software tools for simulating and modeling phase transformation kinetics in materials. These approaches include finite element analysis, molecular dynamics simulations, and machine learning algorithms that predict how materials will transform under various conditions. Simulation techniques help researchers understand complex transformation mechanisms and design materials with specific transformation behaviors without extensive experimental testing.
- Manufacturing processes utilizing controlled phase transformations: Manufacturing techniques that leverage controlled phase transformations to produce materials with enhanced properties. These processes include heat treatments, rapid solidification, and other methods that manipulate the kinetics of phase transformations to achieve desired microstructures. By precisely controlling transformation conditions during processing, manufacturers can optimize material properties such as strength, ductility, and corrosion resistance for specific applications.
02 Heat treatment processes for controlling phase transformations
Heat treatment processes are crucial for controlling phase transformations in materials. These processes involve precise temperature control, specific heating and cooling rates, and carefully designed thermal cycles to achieve desired material properties. By manipulating the thermal history, manufacturers can control the nucleation and growth of new phases, resulting in materials with optimized microstructures and performance characteristics.Expand Specific Solutions03 Computational modeling of phase transformation kinetics
Computational models are developed to simulate and predict phase transformation kinetics in various materials. These models incorporate thermodynamic and kinetic principles to describe nucleation, growth, and overall transformation behavior. Advanced algorithms and simulation techniques enable researchers to understand complex transformation mechanisms, optimize processing parameters, and design materials with specific properties without extensive experimental trials.Expand Specific Solutions04 In-situ monitoring techniques for phase transformations
In-situ monitoring techniques allow real-time observation of phase transformations as they occur in materials. These techniques include specialized microscopy, diffraction methods, and thermal analysis that can capture transformation events during processing. By directly observing transformation phenomena, researchers can better understand kinetic mechanisms, validate theoretical models, and develop more precise control strategies for material processing.Expand Specific Solutions05 Novel materials with controlled phase transformation behavior
Research focuses on developing novel materials with precisely controlled phase transformation behavior. These materials are designed to undergo specific transformations at desired rates and conditions, enabling unique functional properties. By engineering the composition and microstructure, researchers can create materials with enhanced mechanical properties, shape memory effects, or other specialized characteristics that depend on controlled phase transformation kinetics.Expand Specific Solutions
Leading Research Groups and Software Vendors
The finite element implementation of phase transformation kinetics in materials is currently in a growth phase, with increasing market demand driven by advanced manufacturing and materials science applications. The market is expanding as industries seek more accurate simulation tools for material behavior prediction. Leading players include ANSYS, Inc., which dominates the engineering simulation software space with comprehensive phase transformation modeling capabilities. Other significant contributors include academic institutions like Beihang University and Shandong University, which focus on theoretical advancements, while industrial players such as Samsung Electronics, Applied Materials, and QUALCOMM incorporate these technologies into product development. The technology is approaching maturity in traditional applications but continues to evolve for complex multi-physics simulations, with ongoing research to improve computational efficiency and accuracy for real-world material systems.
ANSYS, Inc.
Technical Solution: ANSYS has developed advanced finite element implementation frameworks for phase transformation kinetics in materials through their multiphysics simulation platforms. Their approach integrates thermodynamic and kinetic models with finite element analysis to simulate microstructural evolution during phase transformations. ANSYS employs both phenomenological models (Johnson-Mehl-Avrami-Kolmogorov equations) and phase-field methods to capture the spatial and temporal aspects of phase transformations[1]. Their implementation includes coupled thermal-mechanical-diffusion analyses that account for latent heat effects, volume changes, and stress-induced transformations. ANSYS software incorporates user-defined material models through their proprietary User Material (USERMAT) interface, allowing researchers to implement custom phase transformation kinetics equations within the robust ANSYS solver framework[3]. Their recent developments include machine learning integration to accelerate computation of complex phase diagrams and transformation pathways in multi-component systems.
Strengths: Comprehensive multiphysics coupling capabilities allow simultaneous consideration of thermal, mechanical, and chemical factors affecting phase transformations. Extensive material database and customization options enable modeling of diverse material systems. Weaknesses: Computationally intensive for large-scale simulations with multiple phases, potentially requiring significant hardware resources. Complex implementation requires specialized expertise in both materials science and finite element methods.
Applied Materials, Inc.
Technical Solution: Applied Materials has pioneered finite element implementations for phase transformation kinetics specifically tailored to semiconductor manufacturing processes. Their approach focuses on modeling phase transformations during thin film deposition, thermal annealing, and epitaxial growth processes. The company has developed proprietary algorithms that combine classical nucleation theory with phase-field models to predict microstructural evolution in semiconductor materials[2]. Their implementation incorporates atomic-scale phenomena through kinetic Monte Carlo methods coupled with continuum-level finite element analysis to bridge multiple length scales. Applied Materials' software suite includes specialized modules for modeling solid-state phase transformations in silicon, germanium, and compound semiconductors, with particular emphasis on dopant activation, silicide formation, and crystallization processes[4]. Their recent innovations include AI-enhanced prediction of phase transformation pathways to optimize process parameters for next-generation semiconductor devices with reduced defect densities and improved electrical properties.
Strengths: Highly specialized for semiconductor materials and processes, providing industry-specific solutions with validated accuracy. Integration with process equipment allows direct implementation of simulation results into manufacturing workflows. Weaknesses: Limited applicability outside semiconductor materials and processes. Models may require extensive calibration with experimental data for new material systems or process conditions.
Key Algorithms and Mathematical Frameworks
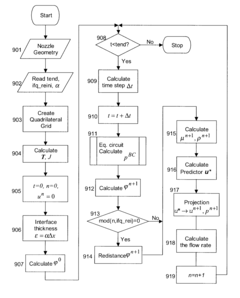
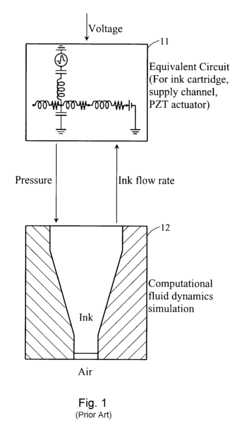
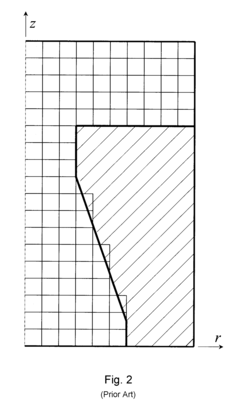
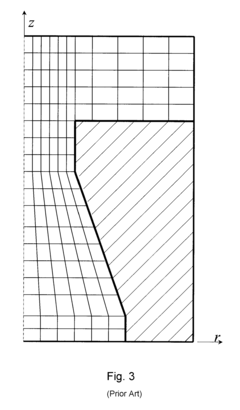
Non-finite element implementation of the finite element projection in two dimensions
PatentInactiveUS8000944B2
Innovation
- A finite difference method and non-finite-element implementation are developed to solve the incompressible continuity equation on quadrilateral grids, transforming the grid to a uniform square grid for easier numerical analysis, resulting in a five-point stencil-based discretization that reduces computational resources and time.
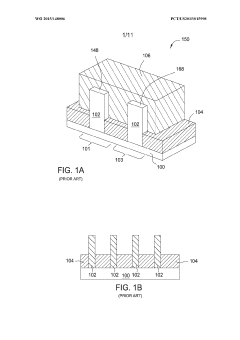
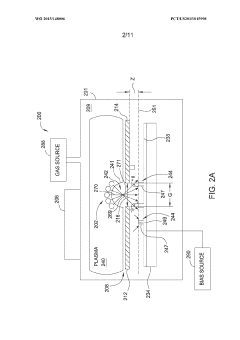
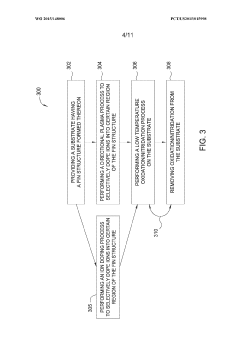
Conversion process utilized for manufacturing advanced 3D features for semiconductor device applications
PatentWO2015148006A1
Innovation
- A conversion process involving a directional plasma doping of specific atoms into fin structures, followed by a surface modification process to replace the initial atoms with desired materials, ensuring precise control over the composition and profile of the fin structures.
Computational Efficiency and Hardware Requirements
The implementation of phase transformation kinetics in materials using finite element methods presents significant computational challenges that directly impact simulation performance and feasibility. Current simulations of complex microstructural evolution typically require substantial computational resources, with high-fidelity models often demanding execution times ranging from several hours to multiple days on standard workstations.
Modern implementations leverage multi-core CPU architectures, with most commercial and research-grade software packages optimized for parallel processing. Benchmarks indicate that phase field models coupled with mechanical deformation can achieve near-linear scaling up to 32-64 CPU cores, though efficiency plateaus beyond this threshold due to communication overhead. Memory requirements are equally demanding, with typical 3D simulations of representative volume elements requiring 16-64GB RAM depending on mesh refinement and model complexity.
GPU acceleration has emerged as a game-changing approach for these computationally intensive simulations. CUDA and OpenCL implementations have demonstrated performance improvements of 10-50x compared to CPU-only solutions, particularly for explicit time-stepping schemes. However, the memory transfer bottleneck between CPU and GPU remains a significant limitation for problems requiring frequent boundary condition updates or adaptive meshing.
Hardware selection critically impacts simulation capabilities. For research environments, workstations with high-frequency CPUs (>3.5GHz), 128GB+ RAM, and professional-grade GPUs with 16GB+ VRAM represent the minimum viable configuration for meaningful 3D simulations. Enterprise-level implementations typically utilize high-performance computing clusters with InfiniBand interconnects to enable domain decomposition across hundreds of compute nodes.
Algorithmic optimizations complement hardware solutions, with adaptive mesh refinement techniques reducing computational requirements by 40-70% compared to uniform meshes. Implicit time-stepping schemes, while computationally intensive per step, allow larger time increments and often result in overall simulation speedup for diffusion-dominated transformations. Recent advances in machine learning surrogate models show promise for accelerating specific components of phase transformation simulations, potentially reducing computation time by orders of magnitude for well-characterized material systems.
Cloud computing platforms now offer viable alternatives to on-premises hardware, with major providers offering specialized instances with high-performance GPUs and large memory configurations. This approach provides scalability advantages but introduces data transfer and security considerations that must be evaluated against specific research or industrial requirements.
Modern implementations leverage multi-core CPU architectures, with most commercial and research-grade software packages optimized for parallel processing. Benchmarks indicate that phase field models coupled with mechanical deformation can achieve near-linear scaling up to 32-64 CPU cores, though efficiency plateaus beyond this threshold due to communication overhead. Memory requirements are equally demanding, with typical 3D simulations of representative volume elements requiring 16-64GB RAM depending on mesh refinement and model complexity.
GPU acceleration has emerged as a game-changing approach for these computationally intensive simulations. CUDA and OpenCL implementations have demonstrated performance improvements of 10-50x compared to CPU-only solutions, particularly for explicit time-stepping schemes. However, the memory transfer bottleneck between CPU and GPU remains a significant limitation for problems requiring frequent boundary condition updates or adaptive meshing.
Hardware selection critically impacts simulation capabilities. For research environments, workstations with high-frequency CPUs (>3.5GHz), 128GB+ RAM, and professional-grade GPUs with 16GB+ VRAM represent the minimum viable configuration for meaningful 3D simulations. Enterprise-level implementations typically utilize high-performance computing clusters with InfiniBand interconnects to enable domain decomposition across hundreds of compute nodes.
Algorithmic optimizations complement hardware solutions, with adaptive mesh refinement techniques reducing computational requirements by 40-70% compared to uniform meshes. Implicit time-stepping schemes, while computationally intensive per step, allow larger time increments and often result in overall simulation speedup for diffusion-dominated transformations. Recent advances in machine learning surrogate models show promise for accelerating specific components of phase transformation simulations, potentially reducing computation time by orders of magnitude for well-characterized material systems.
Cloud computing platforms now offer viable alternatives to on-premises hardware, with major providers offering specialized instances with high-performance GPUs and large memory configurations. This approach provides scalability advantages but introduces data transfer and security considerations that must be evaluated against specific research or industrial requirements.
Validation Methods and Experimental Correlation
Validation of finite element models for phase transformation kinetics requires rigorous methodologies to ensure computational predictions align with real-world material behavior. The primary validation approach involves comparing simulation results with experimental data obtained through various characterization techniques. Dilatometry measurements provide critical information on dimensional changes during phase transformations, offering direct validation points for transformation kinetics models.
X-ray diffraction (XRD) techniques enable quantitative phase analysis during transformation processes, allowing researchers to track phase evolution over time and temperature. These measurements provide essential benchmarks for validating the accuracy of transformation kinetics implementations in finite element models. In-situ XRD during thermal cycling offers particularly valuable validation data as it captures transformation dynamics in real-time.
Microstructural characterization through scanning electron microscopy (SEM) and transmission electron microscopy (TEM) provides morphological validation of transformed phases. The spatial distribution, grain size, and interface characteristics observed experimentally serve as critical validation parameters for finite element simulations. Advanced techniques such as electron backscatter diffraction (EBSD) further enhance validation by providing crystallographic orientation data that can be directly compared with model predictions.
Thermal analysis methods, including differential scanning calorimetry (DSC) and differential thermal analysis (DTA), measure the heat flow associated with phase transformations. These techniques provide transformation temperature ranges and enthalpy changes that serve as thermodynamic validation points for finite element implementations. The comparison between experimental and simulated transformation peaks offers insights into model accuracy.
Statistical validation approaches are increasingly important for robust model assessment. These methods involve multiple experimental trials to establish confidence intervals for transformation parameters, which are then used to evaluate the statistical significance of model predictions. Sensitivity analysis of model parameters against experimental variability helps identify critical factors affecting prediction accuracy.
Multi-scale validation frameworks connect atomistic, mesoscale, and macroscale observations with corresponding simulation hierarchies. This approach ensures consistency across different length scales and provides comprehensive validation of phase transformation kinetics implementations. Benchmark problems with well-characterized experimental datasets serve as standard validation cases for comparing different implementation approaches and computational frameworks.
X-ray diffraction (XRD) techniques enable quantitative phase analysis during transformation processes, allowing researchers to track phase evolution over time and temperature. These measurements provide essential benchmarks for validating the accuracy of transformation kinetics implementations in finite element models. In-situ XRD during thermal cycling offers particularly valuable validation data as it captures transformation dynamics in real-time.
Microstructural characterization through scanning electron microscopy (SEM) and transmission electron microscopy (TEM) provides morphological validation of transformed phases. The spatial distribution, grain size, and interface characteristics observed experimentally serve as critical validation parameters for finite element simulations. Advanced techniques such as electron backscatter diffraction (EBSD) further enhance validation by providing crystallographic orientation data that can be directly compared with model predictions.
Thermal analysis methods, including differential scanning calorimetry (DSC) and differential thermal analysis (DTA), measure the heat flow associated with phase transformations. These techniques provide transformation temperature ranges and enthalpy changes that serve as thermodynamic validation points for finite element implementations. The comparison between experimental and simulated transformation peaks offers insights into model accuracy.
Statistical validation approaches are increasingly important for robust model assessment. These methods involve multiple experimental trials to establish confidence intervals for transformation parameters, which are then used to evaluate the statistical significance of model predictions. Sensitivity analysis of model parameters against experimental variability helps identify critical factors affecting prediction accuracy.
Multi-scale validation frameworks connect atomistic, mesoscale, and macroscale observations with corresponding simulation hierarchies. This approach ensures consistency across different length scales and provides comprehensive validation of phase transformation kinetics implementations. Benchmark problems with well-characterized experimental datasets serve as standard validation cases for comparing different implementation approaches and computational frameworks.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!