Meshless Versus Finite Element Approaches: Comparative Assessment For Specific Problems
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Meshless and FEM Background and Objectives
The evolution of computational mechanics has witnessed significant advancements in numerical methods for solving complex engineering problems. Among these methods, Finite Element Method (FEM) has established itself as the industry standard since its formal development in the 1950s. FEM discretizes the problem domain into elements with predefined shapes, creating a mesh that approximates the geometry and facilitates numerical solutions of partial differential equations governing physical phenomena.
In contrast, Meshless methods emerged in the 1990s as an alternative approach that eliminates the need for explicit mesh generation. These methods approximate solutions using a set of scattered nodes without requiring connectivity information between them. The development of meshless methods was primarily motivated by the challenges associated with mesh generation in FEM, particularly for problems involving large deformations, moving boundaries, and complex geometries.
The technical evolution trajectory shows a clear progression from traditional FEM to various meshless formulations, including Smoothed Particle Hydrodynamics (SPH), Element-Free Galerkin (EFG), Reproducing Kernel Particle Method (RKPM), and Meshless Local Petrov-Galerkin (MLPG) approaches. Each iteration has attempted to address specific limitations while preserving computational accuracy and efficiency.
The primary objective of this comparative assessment is to evaluate the relative strengths and limitations of meshless methods versus FEM for specific engineering problems. We aim to identify scenarios where each approach demonstrates superior performance in terms of accuracy, computational efficiency, implementation complexity, and adaptability to problem characteristics.
This assessment will focus on benchmark problems that highlight the distinctive features of both methodologies, including stress concentration problems, crack propagation analysis, fluid-structure interaction, and problems with moving boundaries. By examining these specific cases, we intend to develop a comprehensive understanding of when meshless methods offer tangible advantages over traditional FEM approaches.
Furthermore, this research seeks to explore the potential for hybrid approaches that leverage the strengths of both methodologies. The integration of meshless techniques in regions requiring special treatment (such as crack tips or high-gradient areas) with conventional FEM in the remainder of the domain represents a promising direction for optimizing computational performance while maintaining solution accuracy.
The ultimate goal is to establish practical guidelines for selecting the most appropriate numerical method based on problem characteristics, available computational resources, and required solution accuracy, thereby enabling more efficient and effective computational solutions for complex engineering challenges.
In contrast, Meshless methods emerged in the 1990s as an alternative approach that eliminates the need for explicit mesh generation. These methods approximate solutions using a set of scattered nodes without requiring connectivity information between them. The development of meshless methods was primarily motivated by the challenges associated with mesh generation in FEM, particularly for problems involving large deformations, moving boundaries, and complex geometries.
The technical evolution trajectory shows a clear progression from traditional FEM to various meshless formulations, including Smoothed Particle Hydrodynamics (SPH), Element-Free Galerkin (EFG), Reproducing Kernel Particle Method (RKPM), and Meshless Local Petrov-Galerkin (MLPG) approaches. Each iteration has attempted to address specific limitations while preserving computational accuracy and efficiency.
The primary objective of this comparative assessment is to evaluate the relative strengths and limitations of meshless methods versus FEM for specific engineering problems. We aim to identify scenarios where each approach demonstrates superior performance in terms of accuracy, computational efficiency, implementation complexity, and adaptability to problem characteristics.
This assessment will focus on benchmark problems that highlight the distinctive features of both methodologies, including stress concentration problems, crack propagation analysis, fluid-structure interaction, and problems with moving boundaries. By examining these specific cases, we intend to develop a comprehensive understanding of when meshless methods offer tangible advantages over traditional FEM approaches.
Furthermore, this research seeks to explore the potential for hybrid approaches that leverage the strengths of both methodologies. The integration of meshless techniques in regions requiring special treatment (such as crack tips or high-gradient areas) with conventional FEM in the remainder of the domain represents a promising direction for optimizing computational performance while maintaining solution accuracy.
The ultimate goal is to establish practical guidelines for selecting the most appropriate numerical method based on problem characteristics, available computational resources, and required solution accuracy, thereby enabling more efficient and effective computational solutions for complex engineering challenges.
Market Applications and Industry Demand Analysis
The market for computational simulation technologies has witnessed significant growth in recent years, with the global Computer-Aided Engineering (CAE) market valued at approximately $7.5 billion in 2022 and projected to reach $16.2 billion by 2030. Within this expanding landscape, both meshless methods and finite element approaches serve distinct market segments with varying requirements and applications.
Aerospace and automotive industries represent the largest consumers of advanced simulation technologies, collectively accounting for over 40% of the total market share. These sectors particularly value meshless methods for complex fluid-structure interaction problems and crash simulations where traditional mesh-based approaches struggle with large deformations. Market research indicates that companies adopting meshless methods for specific applications report up to 30% reduction in simulation preparation time compared to conventional finite element approaches.
The biomedical engineering sector has emerged as a rapidly growing market for simulation technologies, with an annual growth rate exceeding 15%. This industry particularly benefits from meshless methods when modeling soft tissues and complex biological interfaces. However, the established medical device manufacturing segment continues to rely heavily on finite element approaches due to their regulatory acceptance and validation history.
Civil engineering and construction industries maintain strong demand for finite element methods, particularly for structural analysis and building performance simulation. These sectors value the well-established validation protocols and industry standards built around finite element approaches. Market surveys indicate that over 75% of structural engineering firms continue to prefer finite element methods for their core analysis needs.
The energy sector presents a mixed landscape, with oil and gas companies increasingly adopting meshless methods for reservoir simulation and fracture mechanics, while power generation and distribution companies largely maintain finite element workflows for equipment design and infrastructure planning. This sector's annual investment in simulation technologies exceeds $1.2 billion globally.
Software vendors have recognized this diversified market demand, with major CAE providers now offering hybrid solutions that incorporate both meshless and finite element capabilities. This product strategy has expanded their addressable market by approximately 25% over the past five years. The subscription-based simulation software market segment is growing particularly fast at 18% annually, driven by small and medium enterprises seeking flexible access to both computational approaches without significant upfront investment.
Aerospace and automotive industries represent the largest consumers of advanced simulation technologies, collectively accounting for over 40% of the total market share. These sectors particularly value meshless methods for complex fluid-structure interaction problems and crash simulations where traditional mesh-based approaches struggle with large deformations. Market research indicates that companies adopting meshless methods for specific applications report up to 30% reduction in simulation preparation time compared to conventional finite element approaches.
The biomedical engineering sector has emerged as a rapidly growing market for simulation technologies, with an annual growth rate exceeding 15%. This industry particularly benefits from meshless methods when modeling soft tissues and complex biological interfaces. However, the established medical device manufacturing segment continues to rely heavily on finite element approaches due to their regulatory acceptance and validation history.
Civil engineering and construction industries maintain strong demand for finite element methods, particularly for structural analysis and building performance simulation. These sectors value the well-established validation protocols and industry standards built around finite element approaches. Market surveys indicate that over 75% of structural engineering firms continue to prefer finite element methods for their core analysis needs.
The energy sector presents a mixed landscape, with oil and gas companies increasingly adopting meshless methods for reservoir simulation and fracture mechanics, while power generation and distribution companies largely maintain finite element workflows for equipment design and infrastructure planning. This sector's annual investment in simulation technologies exceeds $1.2 billion globally.
Software vendors have recognized this diversified market demand, with major CAE providers now offering hybrid solutions that incorporate both meshless and finite element capabilities. This product strategy has expanded their addressable market by approximately 25% over the past five years. The subscription-based simulation software market segment is growing particularly fast at 18% annually, driven by small and medium enterprises seeking flexible access to both computational approaches without significant upfront investment.
Current State and Technical Challenges
The field of computational mechanics has witnessed significant advancements in both meshless methods and finite element approaches over the past decades. Currently, finite element methods (FEM) remain the dominant industry standard, implemented in major commercial software packages like ANSYS, ABAQUS, and COMSOL. These tools have established robust verification procedures and enjoy widespread adoption across aerospace, automotive, civil engineering, and biomedical industries.
Meshless methods, while theoretically promising, face several implementation challenges that have limited their mainstream adoption. The primary technical hurdle involves the construction of shape functions that satisfy consistency conditions without predefined mesh structures. This fundamental difference creates difficulties in enforcing essential boundary conditions compared to the straightforward approach in FEM.
Recent benchmarking studies reveal that meshless methods demonstrate superior performance in specific problem domains, particularly those involving large deformations, crack propagation, and moving boundaries. However, they typically require higher computational resources for comparable accuracy in standard structural analysis problems. The Element-Free Galerkin (EFG) method and Smoothed Particle Hydrodynamics (SPH) have shown particular promise in fluid-structure interaction problems where traditional FEM approaches struggle with mesh distortion.
A significant technical challenge for meshless methods remains their integration into existing computational frameworks. The absence of standardized implementation protocols and limited commercial software support creates barriers to industrial adoption. Additionally, the mathematical formulation of meshless methods often requires more complex numerical integration schemes, leading to increased computational overhead.
From a geographical perspective, research into meshless methods shows interesting distribution patterns. Asian research institutions, particularly in China and Singapore, have produced substantial theoretical advancements in meshless formulations. European research centers have focused on hybrid approaches that combine meshless and mesh-based techniques, while North American institutions have contributed significantly to verification and validation methodologies.
The computational efficiency gap between the two approaches continues to narrow with hardware advancements. GPU acceleration has shown particular promise for meshless methods due to their inherently parallel nature. However, the lack of robust error estimation techniques for meshless methods remains a critical limitation compared to the well-established error bounds in FEM.
Interoperability between meshless and finite element approaches represents another technical frontier. Current research focuses on developing seamless coupling mechanisms that leverage the strengths of both methodologies within a single simulation framework. This direction shows particular promise for multi-physics problems where different physical phenomena benefit from different discretization approaches.
Meshless methods, while theoretically promising, face several implementation challenges that have limited their mainstream adoption. The primary technical hurdle involves the construction of shape functions that satisfy consistency conditions without predefined mesh structures. This fundamental difference creates difficulties in enforcing essential boundary conditions compared to the straightforward approach in FEM.
Recent benchmarking studies reveal that meshless methods demonstrate superior performance in specific problem domains, particularly those involving large deformations, crack propagation, and moving boundaries. However, they typically require higher computational resources for comparable accuracy in standard structural analysis problems. The Element-Free Galerkin (EFG) method and Smoothed Particle Hydrodynamics (SPH) have shown particular promise in fluid-structure interaction problems where traditional FEM approaches struggle with mesh distortion.
A significant technical challenge for meshless methods remains their integration into existing computational frameworks. The absence of standardized implementation protocols and limited commercial software support creates barriers to industrial adoption. Additionally, the mathematical formulation of meshless methods often requires more complex numerical integration schemes, leading to increased computational overhead.
From a geographical perspective, research into meshless methods shows interesting distribution patterns. Asian research institutions, particularly in China and Singapore, have produced substantial theoretical advancements in meshless formulations. European research centers have focused on hybrid approaches that combine meshless and mesh-based techniques, while North American institutions have contributed significantly to verification and validation methodologies.
The computational efficiency gap between the two approaches continues to narrow with hardware advancements. GPU acceleration has shown particular promise for meshless methods due to their inherently parallel nature. However, the lack of robust error estimation techniques for meshless methods remains a critical limitation compared to the well-established error bounds in FEM.
Interoperability between meshless and finite element approaches represents another technical frontier. Current research focuses on developing seamless coupling mechanisms that leverage the strengths of both methodologies within a single simulation framework. This direction shows particular promise for multi-physics problems where different physical phenomena benefit from different discretization approaches.
Comparative Analysis of Current Solution Approaches
01 Computational efficiency comparison between meshless and FEM
Meshless methods often demonstrate computational advantages over traditional Finite Element Methods (FEM) in certain applications. These methods eliminate the need for mesh generation, which can be time-consuming and error-prone in complex geometries. The computational efficiency is particularly evident in problems involving large deformations, moving boundaries, or crack propagation where mesh distortion in FEM would require remeshing. However, meshless methods may require more computational resources per node due to their more complex shape functions and integration schemes.- Computational efficiency comparison: Meshless methods generally offer computational advantages over traditional Finite Element Methods (FEM) in certain applications. They eliminate the need for mesh generation and remeshing, which can be time-consuming and error-prone in complex geometries or large deformations. This results in reduced preprocessing time and computational resources. However, meshless methods may require more computational effort per node due to more complex shape functions and integration schemes.
- Accuracy and convergence characteristics: The comparative assessment of accuracy between meshless methods and FEM shows that meshless methods can achieve higher order continuity more easily, which is beneficial for solving higher-order differential equations. FEM typically provides better accuracy for lower-order problems with well-structured meshes. Meshless methods often show superior performance in problems involving discontinuities, singularities, or moving boundaries, while FEM maintains advantages in problems with regular domains and standard boundary conditions.
- Implementation complexity and adaptivity: Meshless methods offer greater flexibility in adaptive refinement compared to FEM, as nodes can be added locally without concerning element connectivity. This makes them particularly suitable for problems requiring local refinement or involving evolving geometries. However, meshless methods often have more complex implementation requirements, especially regarding the treatment of essential boundary conditions and numerical integration. FEM benefits from decades of development and standardization, resulting in more mature implementation frameworks and commercial software availability.
- Application-specific performance comparison: The comparative assessment reveals that meshless methods demonstrate superior performance in specific applications such as crack propagation, large deformation problems, fluid-structure interaction, and problems with moving boundaries. FEM remains more efficient and reliable for structural analysis with small deformations, heat transfer in regular domains, and standard engineering applications. The choice between meshless methods and FEM should be guided by the specific requirements of the application, including geometry complexity, expected deformation magnitude, and desired solution properties.
- Hybrid approaches combining meshless and FEM techniques: Hybrid approaches that combine meshless methods and FEM leverage the strengths of both methodologies. These hybrid techniques typically use meshless methods in regions requiring high adaptivity or experiencing large deformations, while employing FEM in regions where traditional elements perform well. This approach optimizes computational efficiency while maintaining solution accuracy across different domain regions. Coupling strategies between meshless and FEM domains represent an active area of research, focusing on ensuring continuity of the solution and its derivatives across the interface between different discretization methods.
02 Accuracy and convergence characteristics
The comparative assessment of accuracy between meshless methods and FEM reveals distinct characteristics. Meshless methods often provide superior accuracy for problems with high gradients or discontinuities due to their flexible approximation capabilities. They can achieve higher-order continuity more naturally than FEM. However, FEM typically demonstrates more predictable convergence rates and well-established error estimation techniques. The accuracy of meshless methods is highly dependent on the choice of shape functions and the distribution of nodes, while FEM accuracy depends primarily on element type and mesh refinement.Expand Specific Solutions03 Implementation complexity and adaptivity
The implementation complexity differs significantly between meshless and finite element methods. FEM benefits from decades of development with established commercial software and standardized procedures, making it more accessible for routine engineering applications. In contrast, meshless methods often require more specialized knowledge for implementation but offer superior adaptivity for certain problems. Meshless methods excel in adaptive refinement scenarios as they allow for straightforward addition or removal of nodes without concerns about element quality or connectivity that plague adaptive FEM implementations.Expand Specific Solutions04 Application-specific performance comparison
The comparative performance of meshless methods versus FEM varies significantly across different application domains. Meshless methods demonstrate superior performance in fluid-structure interaction problems, impact simulations, and biomedical applications with complex geometries or large deformations. FEM remains dominant in structural analysis, heat transfer in regular domains, and applications where established industry standards are important. The choice between these methods often depends on specific problem characteristics such as geometry complexity, material behavior, and required solution properties.Expand Specific Solutions05 Hybrid approaches combining meshless and FEM advantages
Hybrid approaches that combine elements of both meshless methods and FEM have emerged to leverage the strengths of each methodology. These hybrid methods typically use meshless approximations in regions requiring high adaptivity or handling discontinuities, while employing traditional FEM in regular domains where its efficiency and robustness are beneficial. The coupling between meshless and FEM regions presents technical challenges but offers a promising direction for computational mechanics. Such hybrid approaches can optimize computational resources while maintaining solution accuracy across different problem domains.Expand Specific Solutions
Key Research Groups and Software Vendors
The meshless versus finite element approaches market is currently in a growth phase, with increasing adoption across engineering simulation sectors. The global market size for these computational methods is expanding, driven by demand for more accurate and efficient simulation tools in aerospace, automotive, and manufacturing industries. Technologically, finite element methods are more mature, with established players like ANSYS dominating the commercial space, while meshless methods are gaining traction for specific applications where traditional mesh-based approaches face limitations. Leading companies including ANSYS, Boeing, Siemens Industry Software, and Hitachi are investing in hybrid approaches that combine strengths of both methodologies. Academic institutions such as Carnegie Mellon University and Xi'an Jiaotong University are advancing fundamental research, creating a competitive ecosystem where industry-academia partnerships are accelerating innovation and practical implementation.
ANSYS, Inc.
Technical Solution: ANSYS has developed a comprehensive suite of solutions that integrate both meshless and finite element approaches. Their technology combines traditional FEA with meshless methods like Smoothed Particle Hydrodynamics (SPH) and Element-Free Galerkin (EFG) methods. ANSYS Mechanical offers advanced capabilities for handling complex geometries through adaptive mesh refinement while their meshless technologies address problems involving large deformations, material separation, and fluid-structure interactions. Their hybrid approach allows seamless transition between meshed and meshless domains, particularly valuable for multi-physics simulations. ANSYS has implemented specialized algorithms that optimize computational efficiency while maintaining accuracy across different physics domains, enabling engineers to select the most appropriate method based on specific problem characteristics.
Strengths: Comprehensive integration of both methodologies within a unified platform; robust solver technology with extensive material models; advanced adaptive refinement capabilities. Weaknesses: Higher computational requirements for complex meshless simulations; steeper learning curve for users transitioning between methodologies; licensing costs can be prohibitive for smaller organizations.
The Boeing Co.
Technical Solution: Boeing has pioneered proprietary meshless methods specifically tailored for aerospace structural analysis and fluid dynamics simulations. Their approach focuses on particle-based methods and meshless local Petrov-Galerkin techniques that excel in modeling complex aerospace components with irregular geometries and composite materials. Boeing's technology incorporates specialized treatment of boundary conditions and material interfaces critical for aircraft design. Their simulation framework enables multi-scale analysis from component to full-aircraft level, with particular emphasis on damage propagation, impact scenarios, and fatigue analysis where traditional FEA faces limitations. Boeing has developed custom meshless formulations that address the unique challenges of aerospace materials including composites with complex failure modes and non-linear behaviors.
Strengths: Highly specialized for aerospace applications; excellent handling of composite materials and complex geometries; validated against extensive physical testing data. Weaknesses: Solutions are highly domain-specific and may not transfer well to other industries; requires significant computational resources for full-scale aircraft simulations.
Core Algorithms and Mathematical Foundations
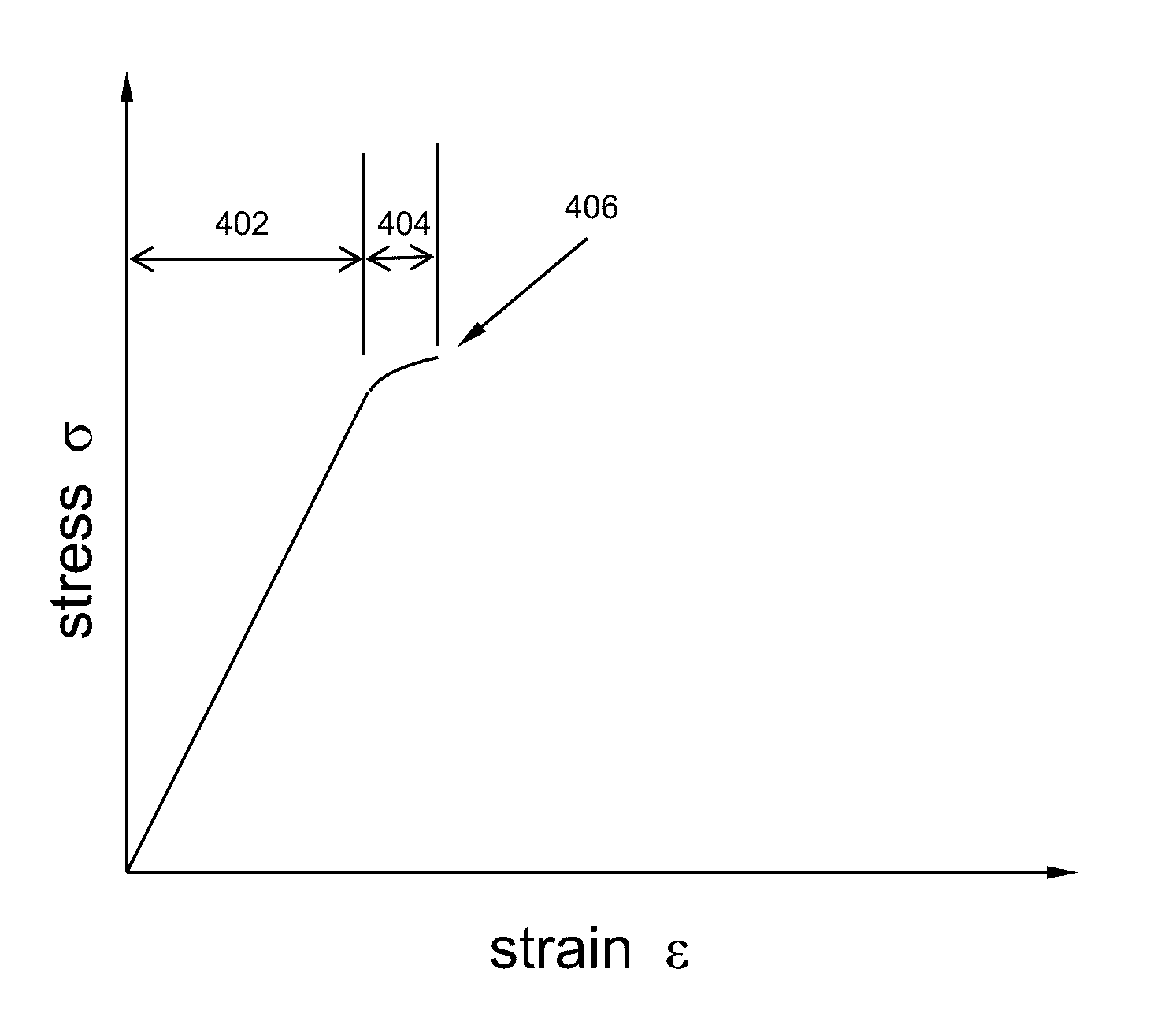
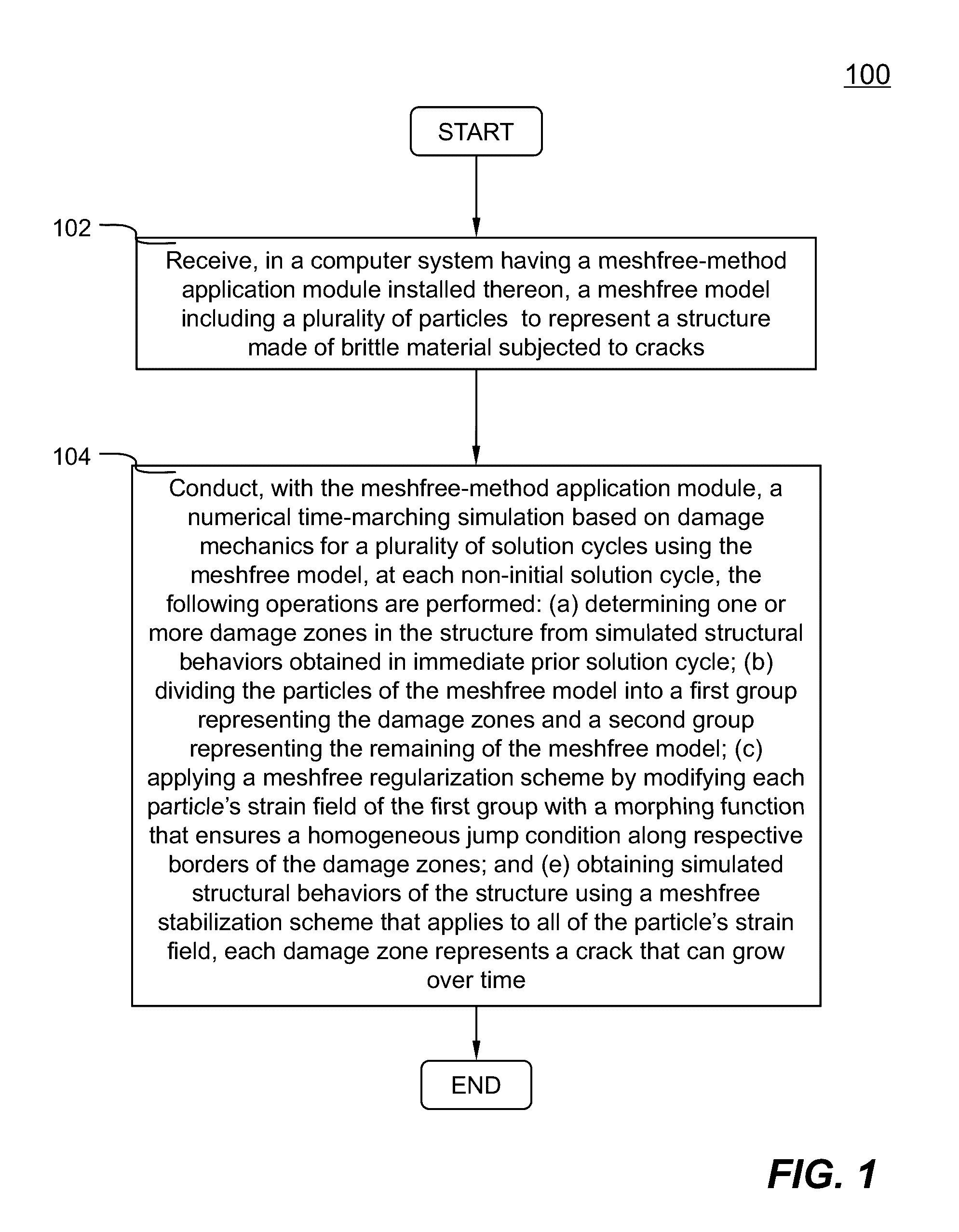
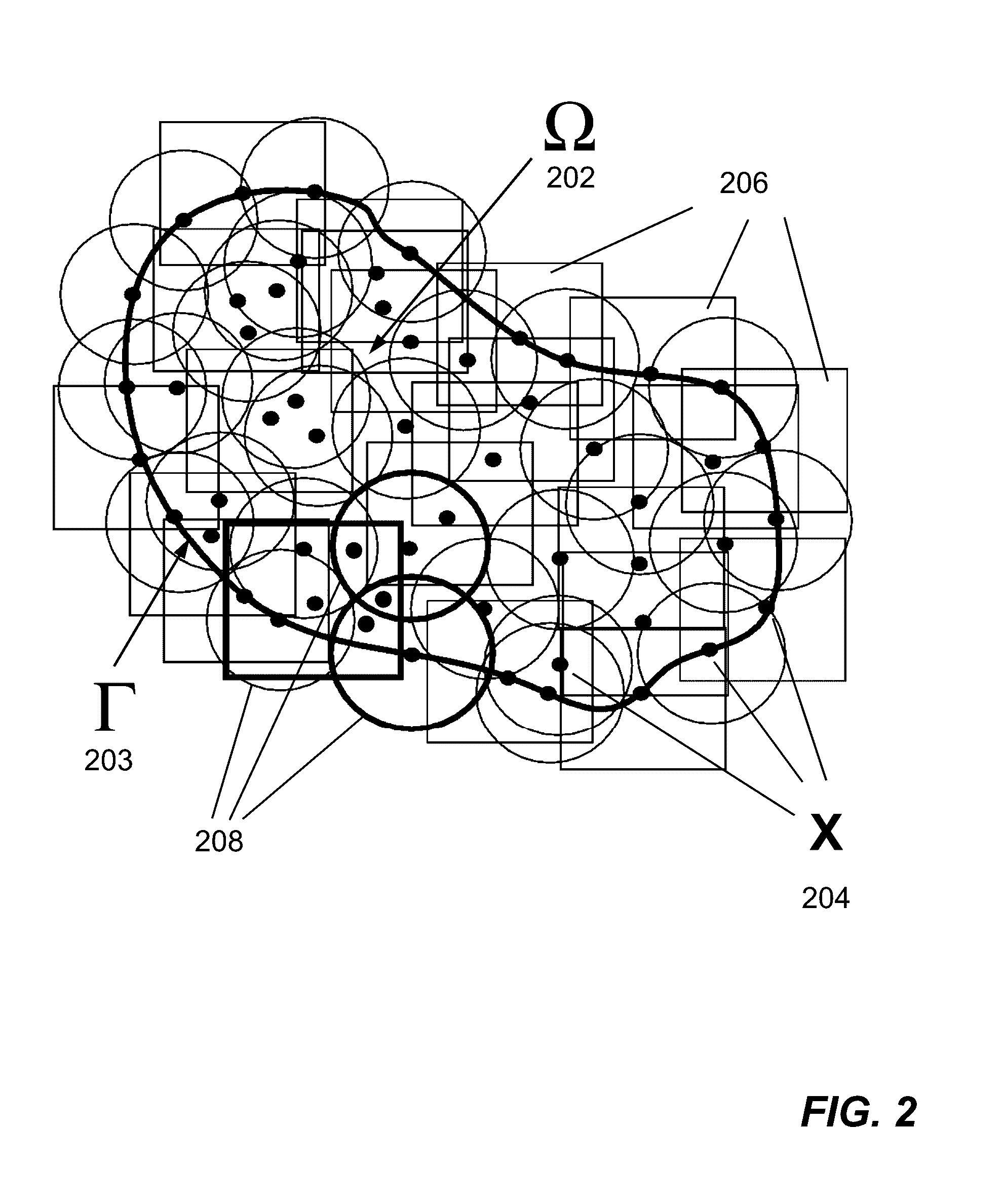
Meshfree Method And System For Numerically Simulating Brittle Material Based On Damage Mechanics
PatentActiveUS20170061042A1
Innovation
- A meshfree model is developed that uses a time-marching simulation based on damage mechanics, where particles are divided into damage zones and undamaged zones, with a morphing function applied to ensure homogeneous strain conditions across damage zones, and a stabilization scheme is used to regularize the strain fields, allowing for the simulation of crack growth over time.
Modelling an object, determination of load capacity, improvement of the design and generating component, and system
PatentPendingUS20230297737A1
Innovation
- The method employs Approximate Convex Decomposition to tessellate CAD models into three-dimensional cells, allowing direct application of boundary conditions and using discontinuous Galerkin or Trefftz methods for numerical simulation, enabling CAD-embedded analysis without meshing and reducing pre-processing time.
Computational Efficiency and Performance Metrics
Computational efficiency represents a critical factor in the selection between meshless methods and finite element methods (FEM) for engineering simulations. When evaluating performance metrics, meshless methods typically demonstrate superior computational efficiency for problems involving large deformations, moving boundaries, and crack propagation. This advantage stems from their ability to avoid remeshing operations that FEM requires when elements become severely distorted, resulting in significant time savings during simulation runtime.
Memory consumption patterns differ substantially between these approaches. FEM generally requires less memory for standard problems with fixed geometries, as its matrix structure is more sparse and banded. Conversely, meshless methods often demand greater memory resources due to their denser influence matrices, particularly when using global basis functions. This difference becomes particularly pronounced in large-scale 3D simulations where memory constraints may become a limiting factor.
Convergence rates present another important performance metric. FEM typically exhibits predictable algebraic convergence rates that depend on the polynomial order of the shape functions. Meshless methods can achieve higher convergence rates for smooth problems, especially when using high-order basis functions, but may suffer from inconsistency issues near boundaries without special treatment. Empirical benchmarks indicate that meshless methods often require fewer nodes than FEM requires elements to achieve comparable accuracy for problems with smooth solutions.
Parallel computing compatibility varies between these approaches. Traditional FEM implementations benefit from decades of optimization for parallel architectures, with well-established domain decomposition techniques. Meshless methods have been catching up in recent years, with research showing promising scalability on GPU architectures due to their more localized computational nature, though they still lag behind in terms of mature parallel implementation frameworks.
Time-to-solution metrics encompass not only raw computational speed but also pre-processing and post-processing efficiency. FEM typically requires significant mesh generation time, which can constitute up to 80% of the total analysis time for complex geometries. Meshless methods substantially reduce this pre-processing overhead, offering significant advantages for rapid prototyping and optimization studies where multiple geometry modifications are required.
Error estimation and adaptive refinement capabilities also impact overall computational efficiency. FEM benefits from well-established error estimators and adaptive refinement strategies. Meshless methods have less mature error estimation techniques, though recent developments in residual-based error indicators show promise for enhancing their adaptive capabilities and further improving their computational efficiency for specific problem classes.
Memory consumption patterns differ substantially between these approaches. FEM generally requires less memory for standard problems with fixed geometries, as its matrix structure is more sparse and banded. Conversely, meshless methods often demand greater memory resources due to their denser influence matrices, particularly when using global basis functions. This difference becomes particularly pronounced in large-scale 3D simulations where memory constraints may become a limiting factor.
Convergence rates present another important performance metric. FEM typically exhibits predictable algebraic convergence rates that depend on the polynomial order of the shape functions. Meshless methods can achieve higher convergence rates for smooth problems, especially when using high-order basis functions, but may suffer from inconsistency issues near boundaries without special treatment. Empirical benchmarks indicate that meshless methods often require fewer nodes than FEM requires elements to achieve comparable accuracy for problems with smooth solutions.
Parallel computing compatibility varies between these approaches. Traditional FEM implementations benefit from decades of optimization for parallel architectures, with well-established domain decomposition techniques. Meshless methods have been catching up in recent years, with research showing promising scalability on GPU architectures due to their more localized computational nature, though they still lag behind in terms of mature parallel implementation frameworks.
Time-to-solution metrics encompass not only raw computational speed but also pre-processing and post-processing efficiency. FEM typically requires significant mesh generation time, which can constitute up to 80% of the total analysis time for complex geometries. Meshless methods substantially reduce this pre-processing overhead, offering significant advantages for rapid prototyping and optimization studies where multiple geometry modifications are required.
Error estimation and adaptive refinement capabilities also impact overall computational efficiency. FEM benefits from well-established error estimators and adaptive refinement strategies. Meshless methods have less mature error estimation techniques, though recent developments in residual-based error indicators show promise for enhancing their adaptive capabilities and further improving their computational efficiency for specific problem classes.
Implementation Considerations and Best Practices
When implementing meshless or finite element methods for specific engineering problems, several critical considerations must be addressed to ensure optimal performance. Hardware requirements differ significantly between these approaches, with meshless methods generally requiring more computational power due to their complex shape function calculations. However, they offer advantages in memory efficiency for certain problem types, particularly those involving large deformations or moving boundaries.
Software implementation presents distinct challenges for each method. Finite element approaches benefit from mature commercial packages with extensive documentation and user support. These established ecosystems provide reliable validation benchmarks and industry-standard workflows. Conversely, meshless methods often require custom code development or specialized libraries, increasing implementation complexity but offering greater flexibility for novel problem formulations.
Integration with existing engineering workflows represents another crucial consideration. Finite element methods typically integrate seamlessly with CAD systems and established design processes. Meshless approaches may require additional preprocessing steps and custom interfaces, potentially disrupting established workflows but enabling more adaptive analysis capabilities.
Error estimation and quality control mechanisms differ fundamentally between these methodologies. Finite element approaches offer well-established error estimators and mesh refinement strategies. Meshless methods provide alternative quality metrics based on node distribution and support domain characteristics, requiring different validation approaches and verification standards.
Computational efficiency trade-offs must be carefully evaluated based on problem characteristics. While finite element methods generally demonstrate superior performance for standard structural analysis, meshless approaches may offer significant advantages for problems involving crack propagation, fluid-structure interaction, or large deformations. The selection should be guided by specific problem requirements rather than general performance metrics.
Best practices for implementation include thorough verification against analytical solutions when available, systematic convergence studies to establish solution reliability, and hybrid approaches that leverage the strengths of both methodologies for complex multi-physics problems. Documentation of validation cases specific to the problem domain ensures reproducibility and builds confidence in the selected approach.
Training requirements for engineering teams should not be underestimated, particularly when transitioning from established finite element workflows to newer meshless methodologies. Investment in specialized training and development of internal expertise significantly impacts successful implementation and long-term sustainability of either approach within organizational contexts.
Software implementation presents distinct challenges for each method. Finite element approaches benefit from mature commercial packages with extensive documentation and user support. These established ecosystems provide reliable validation benchmarks and industry-standard workflows. Conversely, meshless methods often require custom code development or specialized libraries, increasing implementation complexity but offering greater flexibility for novel problem formulations.
Integration with existing engineering workflows represents another crucial consideration. Finite element methods typically integrate seamlessly with CAD systems and established design processes. Meshless approaches may require additional preprocessing steps and custom interfaces, potentially disrupting established workflows but enabling more adaptive analysis capabilities.
Error estimation and quality control mechanisms differ fundamentally between these methodologies. Finite element approaches offer well-established error estimators and mesh refinement strategies. Meshless methods provide alternative quality metrics based on node distribution and support domain characteristics, requiring different validation approaches and verification standards.
Computational efficiency trade-offs must be carefully evaluated based on problem characteristics. While finite element methods generally demonstrate superior performance for standard structural analysis, meshless approaches may offer significant advantages for problems involving crack propagation, fluid-structure interaction, or large deformations. The selection should be guided by specific problem requirements rather than general performance metrics.
Best practices for implementation include thorough verification against analytical solutions when available, systematic convergence studies to establish solution reliability, and hybrid approaches that leverage the strengths of both methodologies for complex multi-physics problems. Documentation of validation cases specific to the problem domain ensures reproducibility and builds confidence in the selected approach.
Training requirements for engineering teams should not be underestimated, particularly when transitioning from established finite element workflows to newer meshless methodologies. Investment in specialized training and development of internal expertise significantly impacts successful implementation and long-term sustainability of either approach within organizational contexts.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!