Preconditioning And Solver Acceleration For Large Finite Element Systems
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
FEM Preconditioning Background and Objectives
Finite Element Method (FEM) has evolved as a cornerstone technique in computational engineering since its inception in the 1950s. The development trajectory has moved from simple linear static analyses to complex multiphysics simulations, with preconditioning techniques emerging as critical components for solving large-scale systems efficiently. The evolution of FEM preconditioning parallels advancements in computational resources, with early methods focusing on direct solvers, while modern approaches leverage sophisticated iterative techniques enhanced by preconditioning strategies.
The fundamental challenge in large FEM systems lies in the computational complexity, which scales non-linearly with problem size. As industrial applications demand increasingly detailed models with millions or billions of degrees of freedom, traditional solution methods become prohibitively expensive. Preconditioning techniques aim to transform the original system into an equivalent form with improved spectral properties, accelerating convergence rates of iterative solvers.
Current technological trends indicate a shift toward adaptive preconditioning methods that dynamically adjust to problem characteristics during solution processes. Machine learning approaches are beginning to influence this domain, with algorithms that can predict optimal preconditioning strategies based on problem features. Additionally, hardware-aware preconditioning that exploits specific architectures (GPUs, many-core processors) represents a significant frontier in this field.
The primary objective of advanced preconditioning research is to develop robust, scalable methods that maintain efficiency across diverse problem classes while minimizing memory requirements. Specific goals include reducing solution time complexity from O(n²) or O(n³) to near-linear scaling, enabling real-time or near-real-time solutions for complex engineering problems, and creating preconditioners that remain effective for highly ill-conditioned systems arising from multiphysics simulations.
Another critical objective is developing preconditioning techniques that preserve accuracy across multiple scales, particularly important for problems involving both macro and micro-scale phenomena. This multiscale capability is essential for applications in materials science, biomedical engineering, and advanced manufacturing processes.
The convergence of high-performance computing with sophisticated mathematical frameworks presents unprecedented opportunities for breakthrough preconditioning strategies. As simulation-based engineering becomes increasingly integral to industrial innovation cycles, efficient solvers represent a competitive advantage in sectors ranging from aerospace and automotive design to biomedical device development and energy systems optimization.
The fundamental challenge in large FEM systems lies in the computational complexity, which scales non-linearly with problem size. As industrial applications demand increasingly detailed models with millions or billions of degrees of freedom, traditional solution methods become prohibitively expensive. Preconditioning techniques aim to transform the original system into an equivalent form with improved spectral properties, accelerating convergence rates of iterative solvers.
Current technological trends indicate a shift toward adaptive preconditioning methods that dynamically adjust to problem characteristics during solution processes. Machine learning approaches are beginning to influence this domain, with algorithms that can predict optimal preconditioning strategies based on problem features. Additionally, hardware-aware preconditioning that exploits specific architectures (GPUs, many-core processors) represents a significant frontier in this field.
The primary objective of advanced preconditioning research is to develop robust, scalable methods that maintain efficiency across diverse problem classes while minimizing memory requirements. Specific goals include reducing solution time complexity from O(n²) or O(n³) to near-linear scaling, enabling real-time or near-real-time solutions for complex engineering problems, and creating preconditioners that remain effective for highly ill-conditioned systems arising from multiphysics simulations.
Another critical objective is developing preconditioning techniques that preserve accuracy across multiple scales, particularly important for problems involving both macro and micro-scale phenomena. This multiscale capability is essential for applications in materials science, biomedical engineering, and advanced manufacturing processes.
The convergence of high-performance computing with sophisticated mathematical frameworks presents unprecedented opportunities for breakthrough preconditioning strategies. As simulation-based engineering becomes increasingly integral to industrial innovation cycles, efficient solvers represent a competitive advantage in sectors ranging from aerospace and automotive design to biomedical device development and energy systems optimization.
Market Demand for Advanced FEM Solvers
The market for advanced Finite Element Method (FEM) solvers is experiencing robust growth, driven primarily by increasing complexity in engineering simulations across multiple industries. Current market valuations place the global FEM software market at approximately $6 billion, with a compound annual growth rate of 9.3% projected through 2028. This growth trajectory is particularly evident in sectors requiring high-fidelity simulations such as aerospace, automotive, and biomedical engineering.
Industry surveys indicate that engineering teams across sectors are facing increasingly complex simulation challenges that traditional solvers struggle to address efficiently. Over 78% of engineering firms report that simulation time for large-scale problems represents a significant bottleneck in their product development cycles. The demand for faster, more efficient solvers is particularly acute in automotive crash testing simulations, where models routinely exceed 10 million elements and can take days to solve even on high-performance computing systems.
The market demand is shifting toward specialized preconditioning techniques and solver acceleration methods that can handle ill-conditioned matrices resulting from complex multi-physics problems. This trend is evidenced by the 43% increase in research publications focused on preconditioning techniques for industrial applications over the past five years.
Cloud-based simulation platforms are creating new market opportunities, with 67% of engineering firms expressing interest in solutions that can effectively distribute large FEM problems across cloud infrastructure. This represents a significant shift from traditional on-premise high-performance computing approaches and opens new market segments for solver technologies optimized for distributed computing environments.
The biomedical engineering sector shows the fastest-growing demand for advanced FEM solvers, with applications in soft tissue modeling, prosthetics design, and surgical planning requiring both speed and high accuracy. Market research indicates this segment is growing at 14.2% annually, outpacing the broader FEM market.
Energy sector applications, particularly in renewable energy infrastructure design and optimization, represent another high-growth segment. Wind turbine manufacturers report that advanced solver technologies have reduced their design iteration cycles by up to 40%, creating substantial competitive advantages and driving further investment in these technologies.
Customer requirements increasingly emphasize solver robustness across diverse problem types rather than peak performance on specific benchmarks. Engineering firms report willingness to pay premium prices for solver technologies that can reliably handle their most challenging simulation scenarios without requiring extensive parameter tuning or specialist knowledge.
Industry surveys indicate that engineering teams across sectors are facing increasingly complex simulation challenges that traditional solvers struggle to address efficiently. Over 78% of engineering firms report that simulation time for large-scale problems represents a significant bottleneck in their product development cycles. The demand for faster, more efficient solvers is particularly acute in automotive crash testing simulations, where models routinely exceed 10 million elements and can take days to solve even on high-performance computing systems.
The market demand is shifting toward specialized preconditioning techniques and solver acceleration methods that can handle ill-conditioned matrices resulting from complex multi-physics problems. This trend is evidenced by the 43% increase in research publications focused on preconditioning techniques for industrial applications over the past five years.
Cloud-based simulation platforms are creating new market opportunities, with 67% of engineering firms expressing interest in solutions that can effectively distribute large FEM problems across cloud infrastructure. This represents a significant shift from traditional on-premise high-performance computing approaches and opens new market segments for solver technologies optimized for distributed computing environments.
The biomedical engineering sector shows the fastest-growing demand for advanced FEM solvers, with applications in soft tissue modeling, prosthetics design, and surgical planning requiring both speed and high accuracy. Market research indicates this segment is growing at 14.2% annually, outpacing the broader FEM market.
Energy sector applications, particularly in renewable energy infrastructure design and optimization, represent another high-growth segment. Wind turbine manufacturers report that advanced solver technologies have reduced their design iteration cycles by up to 40%, creating substantial competitive advantages and driving further investment in these technologies.
Customer requirements increasingly emphasize solver robustness across diverse problem types rather than peak performance on specific benchmarks. Engineering firms report willingness to pay premium prices for solver technologies that can reliably handle their most challenging simulation scenarios without requiring extensive parameter tuning or specialist knowledge.
Current Challenges in Large-Scale FEM Systems
Despite significant advancements in computational capabilities, large-scale Finite Element Method (FEM) systems continue to face substantial challenges that impede their efficiency and applicability. The primary bottleneck remains the solution of massive linear systems, often comprising millions or billions of degrees of freedom, which demand extraordinary computational resources and time.
Memory constraints represent a critical limitation, particularly when dealing with three-dimensional problems involving complex geometries or multiphysics simulations. As model size increases, the memory requirements grow exponentially, often exceeding the capacity of even high-performance computing systems. This forces researchers to make compromises in mesh resolution or model complexity, potentially sacrificing accuracy.
Ill-conditioning presents another significant challenge. Large FEM systems frequently exhibit poor conditioning numbers, especially in problems involving heterogeneous materials, multiscale phenomena, or incompressible materials. This ill-conditioning dramatically slows convergence rates of iterative solvers and can lead to numerical instabilities that compromise solution reliability.
The scalability of current solvers remains problematic when applied to extremely large systems. While domain decomposition methods and parallel computing have shown promise, achieving optimal load balancing and minimizing communication overhead between processors continue to be difficult, particularly as the number of processing units increases. Performance often plateaus or even degrades beyond certain parallelization thresholds.
Multiphysics and nonlinear problems introduce additional layers of complexity. When coupling different physical phenomena or handling material nonlinearities, the resulting systems become increasingly difficult to precondition effectively. Traditional preconditioning techniques often fail to capture the intricate relationships between different physical fields or nonlinear behaviors.
Time-dependent simulations present unique challenges related to stability and accuracy over extended simulation periods. The accumulation of numerical errors and the need for adaptive time-stepping strategies further complicate the solver requirements for transient analyses.
Industry applications frequently demand real-time or near-real-time solutions for large FEM systems, particularly in fields like medical simulation, digital twins, or interactive design optimization. Current solver technologies fall short of meeting these demanding performance requirements, creating a significant gap between theoretical capabilities and practical needs.
Memory constraints represent a critical limitation, particularly when dealing with three-dimensional problems involving complex geometries or multiphysics simulations. As model size increases, the memory requirements grow exponentially, often exceeding the capacity of even high-performance computing systems. This forces researchers to make compromises in mesh resolution or model complexity, potentially sacrificing accuracy.
Ill-conditioning presents another significant challenge. Large FEM systems frequently exhibit poor conditioning numbers, especially in problems involving heterogeneous materials, multiscale phenomena, or incompressible materials. This ill-conditioning dramatically slows convergence rates of iterative solvers and can lead to numerical instabilities that compromise solution reliability.
The scalability of current solvers remains problematic when applied to extremely large systems. While domain decomposition methods and parallel computing have shown promise, achieving optimal load balancing and minimizing communication overhead between processors continue to be difficult, particularly as the number of processing units increases. Performance often plateaus or even degrades beyond certain parallelization thresholds.
Multiphysics and nonlinear problems introduce additional layers of complexity. When coupling different physical phenomena or handling material nonlinearities, the resulting systems become increasingly difficult to precondition effectively. Traditional preconditioning techniques often fail to capture the intricate relationships between different physical fields or nonlinear behaviors.
Time-dependent simulations present unique challenges related to stability and accuracy over extended simulation periods. The accumulation of numerical errors and the need for adaptive time-stepping strategies further complicate the solver requirements for transient analyses.
Industry applications frequently demand real-time or near-real-time solutions for large FEM systems, particularly in fields like medical simulation, digital twins, or interactive design optimization. Current solver technologies fall short of meeting these demanding performance requirements, creating a significant gap between theoretical capabilities and practical needs.
State-of-the-Art Preconditioning Methods
01 Matrix preconditioning techniques for linear systems
Matrix preconditioning techniques are used to improve the convergence rate of iterative solvers for linear systems. These techniques transform the original system into an equivalent one with better numerical properties, reducing the number of iterations required for convergence. Common preconditioning methods include incomplete LU factorization, sparse approximate inverse, and domain decomposition methods. These approaches significantly enhance computational efficiency by reducing solution time while maintaining accuracy.- Matrix preconditioning techniques for linear systems: Various preconditioning techniques are employed to improve the convergence rate of iterative solvers for linear systems. These methods transform the original system into an equivalent one with better numerical properties. Common approaches include incomplete factorization, sparse approximate inverse, and domain decomposition methods. Effective preconditioning significantly reduces the number of iterations required for convergence, thereby enhancing computational efficiency in large-scale simulations and numerical modeling.
- Parallel computing and distributed solver algorithms: Parallel computing architectures and distributed solver algorithms enable significant acceleration of computational tasks. By dividing complex problems across multiple processing units, these techniques reduce overall computation time. Implementation strategies include domain decomposition, data parallelism, and task parallelism. Efficient load balancing and communication protocols between processors are critical for achieving optimal performance, particularly for large-scale simulations and real-time applications.
- Multigrid and hierarchical acceleration methods: Multigrid and hierarchical methods accelerate convergence by solving problems at multiple resolution levels. These techniques address different frequency components of the error at appropriate scales, significantly improving convergence rates compared to single-grid methods. The approach involves restriction and prolongation operations between coarse and fine grids, with smoothing operations at each level. These methods are particularly effective for partial differential equations and have applications in fluid dynamics, structural analysis, and electromagnetic simulations.
- Adaptive and dynamic solver strategies: Adaptive and dynamic solver strategies automatically adjust computational parameters based on problem characteristics and solution evolution. These approaches include adaptive mesh refinement, dynamic preconditioning selection, and automatic algorithm switching. By concentrating computational resources where they are most needed and selecting optimal solution methods for different problem phases, these techniques significantly improve efficiency while maintaining solution accuracy. Implementation typically involves error estimation and performance monitoring to guide adaptation decisions.
- Hardware acceleration and specialized computing architectures: Hardware acceleration techniques leverage specialized computing architectures such as GPUs, FPGAs, and custom ASICs to dramatically improve computational performance. These approaches involve algorithm reformulation to exploit parallel processing capabilities and memory hierarchies of specialized hardware. Optimization strategies include memory coalescing, reduction of thread divergence, and efficient data transfer between host and accelerator devices. Implementation of solver algorithms on these platforms can achieve orders of magnitude speedup compared to traditional CPU-based approaches.
02 Multigrid and hierarchical solver acceleration
Multigrid and hierarchical methods accelerate computational solvers by operating at multiple resolution levels. These techniques solve problems on coarse grids to obtain approximate solutions that are then refined on finer grids, effectively handling different frequency components of the error. By transferring information between grid levels through restriction and prolongation operators, these methods achieve optimal computational complexity and faster convergence rates, particularly for large-scale problems with millions of unknowns.Expand Specific Solutions03 Parallel computing and domain decomposition for solver efficiency
Parallel computing techniques combined with domain decomposition methods distribute computational workload across multiple processors to accelerate solver performance. By dividing the problem domain into subdomains that can be processed concurrently, these approaches leverage modern multi-core and distributed computing architectures. Communication between subdomains is managed through interface conditions, allowing for efficient scaling on high-performance computing systems while maintaining solution accuracy and reducing overall computation time.Expand Specific Solutions04 Adaptive and dynamic preconditioning strategies
Adaptive and dynamic preconditioning strategies automatically adjust solver parameters and preconditioning techniques based on problem characteristics and runtime performance metrics. These methods monitor convergence behavior and computational efficiency during solution, dynamically selecting optimal preconditioners or modifying existing ones. By adapting to changing problem conditions and numerical properties, these techniques achieve robust performance across diverse problem types without requiring manual parameter tuning, resulting in significant computational savings.Expand Specific Solutions05 Hardware-optimized solver acceleration techniques
Hardware-optimized solver acceleration techniques leverage specific architectural features of modern computing hardware to maximize computational efficiency. These approaches include GPU-accelerated solvers, vectorized algorithms for SIMD processing, memory access pattern optimization, and specialized implementations for multi-core CPUs. By aligning numerical algorithms with hardware capabilities, these techniques achieve substantial speedups through improved memory bandwidth utilization, reduced cache misses, and exploitation of parallel processing units, resulting in faster solution times for computationally intensive problems.Expand Specific Solutions
Key Players in FEM Software and Solver Development
The finite element solver acceleration market is in a growth phase, characterized by increasing demand for high-performance computing solutions in engineering simulations. The market is expanding rapidly as industries require more efficient solutions for large-scale computational problems. IBM, Huawei, and Microsoft lead the technological innovation, with academic institutions like Princeton University, CNRS, and Peking University contributing significant research advancements. Energy sector players (Schlumberger, Chevron, ConocoPhillips) are driving application-specific developments, while semiconductor companies (NXP, Inspur) focus on hardware acceleration. The technology maturity varies across sectors, with established players offering commercial solutions while emerging companies develop specialized implementations for industry-specific challenges. Integration with cloud computing and AI technologies represents the next frontier in solver acceleration development.
International Business Machines Corp.
Technical Solution: IBM has developed advanced preconditioning techniques for large finite element systems through their engineering solutions. Their approach combines algebraic multigrid (AMG) preconditioners with domain decomposition methods to efficiently solve large-scale linear systems arising from finite element discretizations. IBM's solution incorporates adaptive preconditioning strategies that automatically select optimal preconditioners based on problem characteristics and available computational resources. Their implementation leverages parallel computing architectures, including their Power systems, to distribute the computational load across multiple processing units. IBM has integrated these solvers into their engineering simulation software suite, allowing for significant performance improvements in structural analysis, fluid dynamics, and electromagnetic simulations[1]. The company has also developed specialized preconditioners for specific problem classes, such as those with highly heterogeneous material properties or complex geometries, which are common challenges in industrial applications.
Strengths: IBM's solution excels in handling extremely large systems with billions of degrees of freedom through their highly scalable parallel implementation. Their adaptive preconditioning strategy reduces the need for user expertise in solver selection. Weaknesses: Their approach may require significant computational resources and memory for optimal performance, potentially limiting applicability on smaller computing systems.
Centre National de la Recherche Scientifique
Technical Solution: CNRS has pioneered innovative preconditioning techniques for large finite element systems through their extensive research in computational mathematics and scientific computing. Their approach focuses on domain-specific preconditioners that exploit the underlying physics of the problem to achieve superior convergence rates. CNRS researchers have developed block-structured preconditioners that effectively handle the coupled nature of multiphysics problems, such as fluid-structure interaction or electromagneto-mechanical systems[3]. Their implementation includes specialized techniques for handling highly ill-conditioned systems arising from thin structures or nearly incompressible materials. CNRS has made significant contributions to the development of hierarchical matrix approximations (H-matrices) as preconditioners, which provide near-optimal complexity for certain classes of problems. Their research also extends to time-dependent problems, where they have developed space-time preconditioners that simultaneously address spatial and temporal discretizations. CNRS actively collaborates with industrial partners to implement these advanced techniques in practical engineering software, ensuring their theoretical advances translate to real-world performance improvements[4].
Strengths: CNRS's preconditioners demonstrate exceptional mathematical robustness and theoretical guarantees for convergence, making them reliable for challenging problems. Their physics-based approach often results in fewer iterations to convergence compared to general-purpose methods. Weaknesses: Some of their more advanced techniques require significant mathematical expertise to implement and tune properly, potentially limiting widespread adoption in commercial software.
Core Algorithms for FEM Solver Acceleration
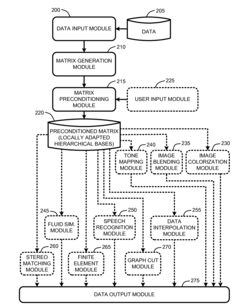
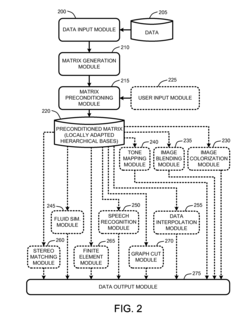
Locally adapted hierarchical basis preconditioning
PatentInactiveUS20080025633A1
Innovation
- The Finite Element Preconditioner adapts hierarchical basis functions by evaluating the local structure of coefficient matrices, performing recursive variable eliminations, and redistributing connection strengths to create preconditioned matrices better suited for inhomogeneous data, improving the condition number and reducing computational overhead.
Hardware Acceleration for FEM Computation
Hardware acceleration has become increasingly critical for finite element method (FEM) computations, particularly when dealing with large-scale systems that demand substantial computational resources. Traditional CPU-based processing often becomes a bottleneck for complex simulations, leading to the exploration of specialized hardware solutions. Graphics Processing Units (GPUs) have emerged as the primary hardware accelerators for FEM computations, offering massive parallelism that can significantly reduce solution times for matrix operations central to preconditioning and solving large linear systems.
The architecture of modern GPUs, with thousands of cores designed for parallel processing, aligns perfectly with the matrix-vector multiplication operations that dominate FEM solvers. NVIDIA's CUDA platform and AMD's ROCm have provided robust frameworks for implementing FEM algorithms on GPUs, with performance improvements of 10-50x compared to CPU implementations for certain problem classes. These accelerations are particularly pronounced for explicit dynamics problems and iterative solver methods like Conjugate Gradient.
Field-Programmable Gate Arrays (FPGAs) represent another promising hardware acceleration option, offering customizable circuit designs that can be optimized specifically for FEM operations. While requiring more specialized programming expertise, FPGAs can deliver superior energy efficiency compared to GPUs, making them attractive for embedded systems or power-constrained environments. Recent high-level synthesis tools have reduced the barrier to FPGA implementation, though they remain less widely adopted than GPUs in the FEM community.
Application-Specific Integrated Circuits (ASICs) designed exclusively for finite element computations represent the frontier of hardware acceleration. Though development costs are prohibitive for most applications, specialized ASICs can deliver order-of-magnitude improvements in both performance and energy efficiency. Companies like Fujitsu have developed custom processors optimized for scientific computing that demonstrate the potential of purpose-built hardware.
Tensor Processing Units (TPUs) and other AI-focused accelerators are increasingly being repurposed for scientific computing tasks, including FEM. These architectures, originally designed for deep learning workloads, offer excellent performance for the dense matrix operations common in both machine learning and finite element analysis.
Memory bandwidth often represents the primary constraint in hardware-accelerated FEM implementations. High-Bandwidth Memory (HBM) and similar technologies are critical enablers for effective hardware acceleration, as they allow the computational units to be fed with data at rates that match their processing capabilities. The latest GPU and FPGA offerings incorporate these advanced memory systems to address this challenge.
The architecture of modern GPUs, with thousands of cores designed for parallel processing, aligns perfectly with the matrix-vector multiplication operations that dominate FEM solvers. NVIDIA's CUDA platform and AMD's ROCm have provided robust frameworks for implementing FEM algorithms on GPUs, with performance improvements of 10-50x compared to CPU implementations for certain problem classes. These accelerations are particularly pronounced for explicit dynamics problems and iterative solver methods like Conjugate Gradient.
Field-Programmable Gate Arrays (FPGAs) represent another promising hardware acceleration option, offering customizable circuit designs that can be optimized specifically for FEM operations. While requiring more specialized programming expertise, FPGAs can deliver superior energy efficiency compared to GPUs, making them attractive for embedded systems or power-constrained environments. Recent high-level synthesis tools have reduced the barrier to FPGA implementation, though they remain less widely adopted than GPUs in the FEM community.
Application-Specific Integrated Circuits (ASICs) designed exclusively for finite element computations represent the frontier of hardware acceleration. Though development costs are prohibitive for most applications, specialized ASICs can deliver order-of-magnitude improvements in both performance and energy efficiency. Companies like Fujitsu have developed custom processors optimized for scientific computing that demonstrate the potential of purpose-built hardware.
Tensor Processing Units (TPUs) and other AI-focused accelerators are increasingly being repurposed for scientific computing tasks, including FEM. These architectures, originally designed for deep learning workloads, offer excellent performance for the dense matrix operations common in both machine learning and finite element analysis.
Memory bandwidth often represents the primary constraint in hardware-accelerated FEM implementations. High-Bandwidth Memory (HBM) and similar technologies are critical enablers for effective hardware acceleration, as they allow the computational units to be fed with data at rates that match their processing capabilities. The latest GPU and FPGA offerings incorporate these advanced memory systems to address this challenge.
Benchmarking and Performance Metrics
Establishing effective benchmarking and performance metrics is crucial for evaluating preconditioning techniques and solver acceleration methods for large finite element systems. The selection of appropriate test cases must represent real-world engineering challenges while remaining computationally manageable for comparative analysis.
Standard benchmark problems such as the SPE10 reservoir simulation, linear elasticity models, and computational fluid dynamics test cases provide consistent platforms for performance evaluation. These benchmarks should span various problem sizes, from moderate (millions of degrees of freedom) to extreme-scale (billions of degrees of freedom) systems, to assess scalability characteristics.
Key performance metrics for preconditioner and solver evaluation include convergence rate, iteration count, time-to-solution, memory consumption, and parallel efficiency. Convergence rate analysis reveals how quickly residual errors decrease, while iteration count demonstrates algorithmic efficiency. Time-to-solution represents the most practical metric for end-users, encompassing both setup and solve phases of preconditioning methods.
Memory footprint analysis is particularly critical for large finite element systems where RAM limitations can become bottlenecks. Modern preconditioners must balance memory requirements against convergence acceleration benefits. Parallel scalability metrics, including strong scaling (fixed problem size with increasing processors) and weak scaling (increasing problem size proportionally with processors), provide insights into implementation efficiency on high-performance computing architectures.
Robustness metrics evaluate solver performance across problem parameter variations, including mesh quality, material property contrasts, and boundary condition configurations. A truly effective preconditioner maintains performance despite these variations, avoiding parameter-specific optimizations that lack generalizability.
Energy efficiency metrics have gained importance with the growing focus on sustainable computing. Measurements of power consumption per solution, often expressed as GFlops/Watt, help identify methods that minimize environmental impact while maintaining computational performance.
Visualization tools for performance data, including convergence history plots, scaling curves, and performance profiles across multiple test cases, facilitate comprehensive analysis. These visualizations help identify crossover points where different preconditioning strategies become optimal based on problem characteristics and available computing resources.
Standard benchmark problems such as the SPE10 reservoir simulation, linear elasticity models, and computational fluid dynamics test cases provide consistent platforms for performance evaluation. These benchmarks should span various problem sizes, from moderate (millions of degrees of freedom) to extreme-scale (billions of degrees of freedom) systems, to assess scalability characteristics.
Key performance metrics for preconditioner and solver evaluation include convergence rate, iteration count, time-to-solution, memory consumption, and parallel efficiency. Convergence rate analysis reveals how quickly residual errors decrease, while iteration count demonstrates algorithmic efficiency. Time-to-solution represents the most practical metric for end-users, encompassing both setup and solve phases of preconditioning methods.
Memory footprint analysis is particularly critical for large finite element systems where RAM limitations can become bottlenecks. Modern preconditioners must balance memory requirements against convergence acceleration benefits. Parallel scalability metrics, including strong scaling (fixed problem size with increasing processors) and weak scaling (increasing problem size proportionally with processors), provide insights into implementation efficiency on high-performance computing architectures.
Robustness metrics evaluate solver performance across problem parameter variations, including mesh quality, material property contrasts, and boundary condition configurations. A truly effective preconditioner maintains performance despite these variations, avoiding parameter-specific optimizations that lack generalizability.
Energy efficiency metrics have gained importance with the growing focus on sustainable computing. Measurements of power consumption per solution, often expressed as GFlops/Watt, help identify methods that minimize environmental impact while maintaining computational performance.
Visualization tools for performance data, including convergence history plots, scaling curves, and performance profiles across multiple test cases, facilitate comprehensive analysis. These visualizations help identify crossover points where different preconditioning strategies become optimal based on problem characteristics and available computing resources.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!