Finite Element Modeling Of Poromechanics: Coupled Flow And Deformation
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Poromechanics Background and Research Objectives
Poromechanics emerged in the mid-20th century through the pioneering work of Maurice Biot, who established the theoretical foundation for understanding the coupled behavior of fluid flow and solid deformation in porous media. This interdisciplinary field combines principles from soil mechanics, rock mechanics, fluid dynamics, and structural engineering to address complex multiphysics problems. Over the decades, poromechanics has evolved from simplified analytical models to sophisticated computational frameworks capable of simulating increasingly complex scenarios across various scales.
The evolution of poromechanics has been closely tied to advancements in computational capabilities. Early models were limited to one-dimensional problems with simplistic assumptions, while contemporary approaches incorporate three-dimensional heterogeneous domains with nonlinear material behavior, multiphase flow, and complex boundary conditions. The finite element method has emerged as a particularly powerful tool for poromechanical modeling due to its flexibility in handling irregular geometries and heterogeneous material properties.
Recent technological trends in poromechanics include the integration of machine learning techniques to enhance computational efficiency, the development of multiscale modeling approaches to bridge micro and macro behaviors, and the incorporation of thermodynamic principles for more accurate representation of coupled processes. These advancements are driven by the growing need to address critical challenges in energy resource extraction, environmental protection, and infrastructure sustainability.
The primary objective of this technical research is to comprehensively evaluate the current state of finite element modeling techniques for coupled flow and deformation in porous media. We aim to identify the most effective numerical formulations, solution algorithms, and implementation strategies that accurately capture the complex interplay between fluid transport and mechanical deformation across different time and spatial scales.
Specifically, this research seeks to assess various finite element discretization schemes for poroelastic problems, including mixed formulations, stabilized methods, and enriched approximations. We will examine their performance in terms of accuracy, stability, computational efficiency, and applicability to practical engineering problems. Additionally, we aim to identify the challenges associated with nonlinear material behavior, large deformations, and multiphase flow scenarios that are increasingly relevant in advanced applications.
Furthermore, this investigation will explore emerging computational techniques that show promise for enhancing the capabilities of poromechanical modeling, such as adaptive mesh refinement, reduced-order modeling, and parallel computing strategies. By establishing a clear understanding of the strengths and limitations of current approaches, this research will provide valuable insights for future development directions and potential breakthrough points in poromechanical simulation technology.
The evolution of poromechanics has been closely tied to advancements in computational capabilities. Early models were limited to one-dimensional problems with simplistic assumptions, while contemporary approaches incorporate three-dimensional heterogeneous domains with nonlinear material behavior, multiphase flow, and complex boundary conditions. The finite element method has emerged as a particularly powerful tool for poromechanical modeling due to its flexibility in handling irregular geometries and heterogeneous material properties.
Recent technological trends in poromechanics include the integration of machine learning techniques to enhance computational efficiency, the development of multiscale modeling approaches to bridge micro and macro behaviors, and the incorporation of thermodynamic principles for more accurate representation of coupled processes. These advancements are driven by the growing need to address critical challenges in energy resource extraction, environmental protection, and infrastructure sustainability.
The primary objective of this technical research is to comprehensively evaluate the current state of finite element modeling techniques for coupled flow and deformation in porous media. We aim to identify the most effective numerical formulations, solution algorithms, and implementation strategies that accurately capture the complex interplay between fluid transport and mechanical deformation across different time and spatial scales.
Specifically, this research seeks to assess various finite element discretization schemes for poroelastic problems, including mixed formulations, stabilized methods, and enriched approximations. We will examine their performance in terms of accuracy, stability, computational efficiency, and applicability to practical engineering problems. Additionally, we aim to identify the challenges associated with nonlinear material behavior, large deformations, and multiphase flow scenarios that are increasingly relevant in advanced applications.
Furthermore, this investigation will explore emerging computational techniques that show promise for enhancing the capabilities of poromechanical modeling, such as adaptive mesh refinement, reduced-order modeling, and parallel computing strategies. By establishing a clear understanding of the strengths and limitations of current approaches, this research will provide valuable insights for future development directions and potential breakthrough points in poromechanical simulation technology.
Market Applications and Industry Demand Analysis
The market for finite element modeling of poromechanics, particularly coupled flow and deformation analysis, has experienced significant growth across multiple industries. This technology addresses critical needs in sectors where understanding the interaction between fluid flow and structural deformation in porous media is essential for operational safety, resource optimization, and environmental protection.
In the oil and gas industry, poromechanical modeling has become indispensable for reservoir management, wellbore stability analysis, and hydraulic fracturing operations. The global hydraulic fracturing market, where this technology is heavily utilized, was valued at approximately $50 billion in 2022 and continues to grow as unconventional resource development expands globally. Companies are increasingly demanding more sophisticated modeling capabilities to optimize production while minimizing environmental impacts.
The geotechnical engineering sector represents another substantial market, with applications in foundation design, slope stability analysis, and underground construction. The global geotechnical engineering market, estimated at $18 billion, is projected to grow at a compound annual rate of 6.5% through 2028, driven by increasing infrastructure development and urbanization worldwide.
Carbon capture and storage (CCS) initiatives have emerged as a rapidly growing application area. As governments worldwide commit to carbon reduction targets, investment in CCS technologies has surged, creating demand for advanced poromechanical modeling to ensure safe and effective subsurface CO2 storage. The global CCS market is expected to reach $7 billion by 2030, with modeling services comprising a significant portion of project development costs.
The biomedical engineering field represents an emerging market for poromechanical modeling, particularly in tissue engineering and drug delivery systems. Research funding in this area has increased substantially, with public and private investments exceeding $3 billion annually in advanced biomechanical modeling and simulation technologies.
Water resource management applications, including groundwater remediation and aquifer management, constitute another growing market segment. With increasing water scarcity concerns globally, the demand for sophisticated hydrogeological modeling capabilities has risen sharply, with the global water management solutions market approaching $30 billion.
Industry demand is increasingly focused on integrated modeling platforms that can handle multiphysics problems efficiently while providing user-friendly interfaces for non-specialists. There is particular interest in real-time simulation capabilities and cloud-based solutions that can process large datasets and complex geometries without requiring extensive computational infrastructure.
In the oil and gas industry, poromechanical modeling has become indispensable for reservoir management, wellbore stability analysis, and hydraulic fracturing operations. The global hydraulic fracturing market, where this technology is heavily utilized, was valued at approximately $50 billion in 2022 and continues to grow as unconventional resource development expands globally. Companies are increasingly demanding more sophisticated modeling capabilities to optimize production while minimizing environmental impacts.
The geotechnical engineering sector represents another substantial market, with applications in foundation design, slope stability analysis, and underground construction. The global geotechnical engineering market, estimated at $18 billion, is projected to grow at a compound annual rate of 6.5% through 2028, driven by increasing infrastructure development and urbanization worldwide.
Carbon capture and storage (CCS) initiatives have emerged as a rapidly growing application area. As governments worldwide commit to carbon reduction targets, investment in CCS technologies has surged, creating demand for advanced poromechanical modeling to ensure safe and effective subsurface CO2 storage. The global CCS market is expected to reach $7 billion by 2030, with modeling services comprising a significant portion of project development costs.
The biomedical engineering field represents an emerging market for poromechanical modeling, particularly in tissue engineering and drug delivery systems. Research funding in this area has increased substantially, with public and private investments exceeding $3 billion annually in advanced biomechanical modeling and simulation technologies.
Water resource management applications, including groundwater remediation and aquifer management, constitute another growing market segment. With increasing water scarcity concerns globally, the demand for sophisticated hydrogeological modeling capabilities has risen sharply, with the global water management solutions market approaching $30 billion.
Industry demand is increasingly focused on integrated modeling platforms that can handle multiphysics problems efficiently while providing user-friendly interfaces for non-specialists. There is particular interest in real-time simulation capabilities and cloud-based solutions that can process large datasets and complex geometries without requiring extensive computational infrastructure.
Current Challenges in Coupled Flow-Deformation Modeling
Despite significant advancements in poromechanical modeling, several critical challenges persist in accurately representing coupled flow-deformation processes. The fundamental difficulty lies in the inherent multiphysics nature of poromechanics, where fluid flow and solid deformation interact through complex feedback mechanisms that operate across multiple spatial and temporal scales.
Numerical instabilities remain a persistent obstacle, particularly when modeling highly heterogeneous porous media with sharp contrasts in material properties. These instabilities often manifest as oscillations in pressure and displacement fields, requiring sophisticated stabilization techniques that may compromise solution accuracy or computational efficiency.
Computational expense presents another significant barrier, especially for large-scale, three-dimensional problems with complex geometries. The coupled system of equations demands substantial computational resources, with solution times that can become prohibitive for practical engineering applications. This challenge is exacerbated when incorporating nonlinear material behaviors or time-dependent processes that require small time steps.
The accurate representation of material interfaces and discontinuities continues to challenge existing finite element frameworks. Traditional methods often struggle to capture sharp fronts in fluid pressure or stress concentrations near fractures, faults, or material boundaries without excessive mesh refinement or specialized numerical treatments.
Constitutive modeling represents perhaps the most fundamental challenge, as the complex relationships between stress, strain, fluid pressure, and permeability remain difficult to characterize experimentally and implement numerically. Many existing models rely on simplifying assumptions that may not adequately represent the full range of behaviors observed in real materials.
Time-scale disparities between fluid flow and mechanical deformation processes create additional complications. Flow processes often occur much more rapidly than mechanical deformation in certain materials, leading to stiff equation systems that require specialized time-stepping schemes to solve efficiently.
Validation and uncertainty quantification present methodological challenges, as laboratory experiments may not fully replicate field conditions, and field measurements typically provide limited spatial and temporal resolution. This gap between model predictions and observable data complicates the assessment of model accuracy and reliability.
Integration with other physical processes, such as thermal effects, chemical reactions, or biological activities, introduces additional coupling mechanisms that further complicate the mathematical formulation and numerical solution of poromechanical problems, yet are essential for many practical applications.
Numerical instabilities remain a persistent obstacle, particularly when modeling highly heterogeneous porous media with sharp contrasts in material properties. These instabilities often manifest as oscillations in pressure and displacement fields, requiring sophisticated stabilization techniques that may compromise solution accuracy or computational efficiency.
Computational expense presents another significant barrier, especially for large-scale, three-dimensional problems with complex geometries. The coupled system of equations demands substantial computational resources, with solution times that can become prohibitive for practical engineering applications. This challenge is exacerbated when incorporating nonlinear material behaviors or time-dependent processes that require small time steps.
The accurate representation of material interfaces and discontinuities continues to challenge existing finite element frameworks. Traditional methods often struggle to capture sharp fronts in fluid pressure or stress concentrations near fractures, faults, or material boundaries without excessive mesh refinement or specialized numerical treatments.
Constitutive modeling represents perhaps the most fundamental challenge, as the complex relationships between stress, strain, fluid pressure, and permeability remain difficult to characterize experimentally and implement numerically. Many existing models rely on simplifying assumptions that may not adequately represent the full range of behaviors observed in real materials.
Time-scale disparities between fluid flow and mechanical deformation processes create additional complications. Flow processes often occur much more rapidly than mechanical deformation in certain materials, leading to stiff equation systems that require specialized time-stepping schemes to solve efficiently.
Validation and uncertainty quantification present methodological challenges, as laboratory experiments may not fully replicate field conditions, and field measurements typically provide limited spatial and temporal resolution. This gap between model predictions and observable data complicates the assessment of model accuracy and reliability.
Integration with other physical processes, such as thermal effects, chemical reactions, or biological activities, introduces additional coupling mechanisms that further complicate the mathematical formulation and numerical solution of poromechanical problems, yet are essential for many practical applications.
State-of-the-Art Numerical Solution Approaches
01 Numerical methods for coupled flow and deformation modeling
Various numerical methods are employed to model coupled flow and deformation in poromechanics. These methods include finite element analysis, finite difference methods, and hybrid approaches that can handle the complex interactions between fluid flow and solid deformation in porous media. These computational techniques enable accurate simulation of stress-dependent permeability, pressure-dependent deformation, and other coupled phenomena in applications such as reservoir engineering and geomechanics.- Numerical methods for coupled poromechanical simulations: Various numerical methods are employed to solve coupled poromechanical problems involving fluid flow and deformation. These methods include finite element modeling, finite difference methods, and hybrid approaches that can handle the complex interactions between fluid pressure and solid matrix deformation. Advanced algorithms are developed to ensure stability and accuracy in simulations, particularly for heterogeneous and anisotropic media where traditional methods may face convergence issues.
- Reservoir simulation and hydrocarbon extraction modeling: Poromechanical modeling is extensively used in reservoir engineering to simulate fluid flow and geomechanical deformation in oil and gas reservoirs. These models account for multiphase flow, pressure changes during extraction, and the resulting deformation of the reservoir rock. The coupled simulations help in predicting reservoir performance, optimizing well placement, and preventing issues like subsidence or wellbore instability during hydrocarbon extraction operations.
- Fracture propagation and geomechanical analysis: Finite element models are developed to simulate fracture initiation and propagation in porous media under coupled flow and deformation conditions. These models incorporate poroelastic theory to account for how fluid pressure affects stress distribution and fracture behavior. Applications include hydraulic fracturing operations, geothermal reservoir stimulation, and analysis of natural fracture networks in subsurface formations.
- Multi-scale and multi-physics coupling approaches: Advanced modeling techniques address the multi-scale and multi-physics nature of poromechanical problems. These approaches integrate phenomena occurring at different spatial and temporal scales, from pore-level fluid-solid interactions to field-scale deformations. The models couple various physical processes including fluid flow, heat transfer, chemical reactions, and mechanical deformation to provide comprehensive simulations of complex subsurface systems.
- Machine learning and optimization for poromechanical modeling: Innovative approaches incorporate machine learning and optimization techniques to enhance poromechanical simulations. These methods improve computational efficiency, parameter estimation, and uncertainty quantification in coupled flow-deformation models. Data-driven approaches are used to develop surrogate models that can rapidly approximate complex poromechanical behavior, enabling real-time decision making for applications in geotechnical engineering, petroleum production, and carbon sequestration.
02 Reservoir simulation and optimization techniques
Advanced simulation techniques are developed for modeling fluid flow and geomechanical deformation in hydrocarbon reservoirs. These techniques incorporate poromechanical principles to predict reservoir behavior during production operations. The models account for multiphase flow, fracture propagation, and formation damage, enabling better reservoir management decisions. Optimization algorithms are integrated with these simulations to maximize recovery while minimizing environmental impact and operational costs.Expand Specific Solutions03 Fracture modeling in poroelastic media
Specialized modeling approaches are developed for simulating fracture initiation, propagation, and interaction in poroelastic media. These models incorporate the effects of fluid pressure on fracture mechanics and the reciprocal influence of fractures on fluid flow patterns. The coupled nature of these processes requires sophisticated numerical techniques that can handle discontinuities in the solution domain while maintaining computational efficiency and accuracy for practical engineering applications.Expand Specific Solutions04 Multi-scale and multi-physics modeling frameworks
Comprehensive modeling frameworks are designed to address the multi-scale and multi-physics nature of poromechanical problems. These frameworks integrate different physical processes occurring at various spatial and temporal scales, from pore-scale fluid dynamics to field-scale deformation. Advanced coupling schemes are implemented to ensure consistent information transfer between different physics modules and scale levels, enabling more realistic simulation of complex subsurface systems and engineered porous materials.Expand Specific Solutions05 Real-time simulation and visualization techniques
Innovative approaches for real-time simulation and visualization of coupled flow and deformation processes are developed to support decision-making in field operations. These techniques employ model reduction methods, parallel computing architectures, and advanced graphics processing to deliver timely insights into system behavior. Interactive visualization tools allow engineers to explore simulation results, identify critical phenomena, and evaluate alternative scenarios efficiently, bridging the gap between complex numerical models and practical engineering applications.Expand Specific Solutions
Leading Research Groups and Software Developers
The field of poromechanics finite element modeling is currently in a growth phase, with an estimated market size of $500-700 million and expanding at 8-10% annually. The competitive landscape features a mix of academic institutions and industry players, with universities dominating fundamental research while oil and gas companies lead commercial applications. Key academic players include the University of Wyoming, Dalian University of Technology, and China University of Petroleum, focusing on theoretical advancements. On the industry side, Schlumberger, Saudi Aramco, and Chevron are investing heavily in practical applications. The technology has reached moderate maturity in conventional applications but remains emerging in complex scenarios like unconventional reservoirs and carbon sequestration, with significant R&D still underway to address computational challenges and multi-physics coupling.
Schlumberger Technologies, Inc.
Technical Solution: Schlumberger has developed advanced finite element modeling techniques for poromechanics that integrate coupled flow and deformation processes in reservoir simulation. Their INTERSECT reservoir simulator incorporates fully coupled poroelastic models that account for the interaction between fluid flow and rock deformation in heterogeneous porous media. The company utilizes adaptive mesh refinement techniques to enhance computational efficiency while maintaining accuracy in complex geological structures. Schlumberger's approach implements implicit time-stepping schemes that ensure numerical stability for highly nonlinear coupled problems, particularly in low-permeability formations where pressure and stress coupling is significant. Their models incorporate multiphase flow capabilities with constitutive relationships that account for stress-dependent permeability and porosity changes during production or injection operations.
Strengths: Industry-leading integration of complex geological features with robust numerical solvers; extensive field validation across diverse reservoir types; superior handling of nonlinear coupling effects. Weaknesses: Computationally intensive for full-field models; requires significant expertise to properly calibrate and interpret results; proprietary nature limits academic collaboration and transparency.
Saudi Arabian Oil Co.
Technical Solution: Saudi Aramco has developed sophisticated finite element modeling capabilities for poromechanics focusing on carbonate reservoirs with complex natural fracture networks. Their approach implements a fully coupled thermo-hydro-mechanical (THM) framework that addresses the unique challenges of Middle Eastern reservoir systems. The company's proprietary simulator employs mixed finite element formulations that ensure local mass conservation while accurately representing stress distributions at fracture interfaces. Aramco's models incorporate advanced constitutive relationships for carbonate rocks that account for pressure solution, compaction, and diagenetic processes affecting long-term reservoir performance. Their technology includes specialized treatment of wettability alteration effects on relative permeability and capillary pressure during enhanced oil recovery operations. The company has validated their models through extensive field testing in giant carbonate reservoirs, demonstrating the ability to predict subsidence, fault reactivation risks, and production-induced stress changes.
Strengths: Unparalleled expertise in carbonate reservoir poromechanics; extensive field data for model calibration; integration with comprehensive reservoir management workflows. Weaknesses: Models optimized for specific geological settings may have limited applicability elsewhere; computational demands can restrict full-field implementation; proprietary nature limits external scientific scrutiny.
Key Algorithms and Mathematical Formulations
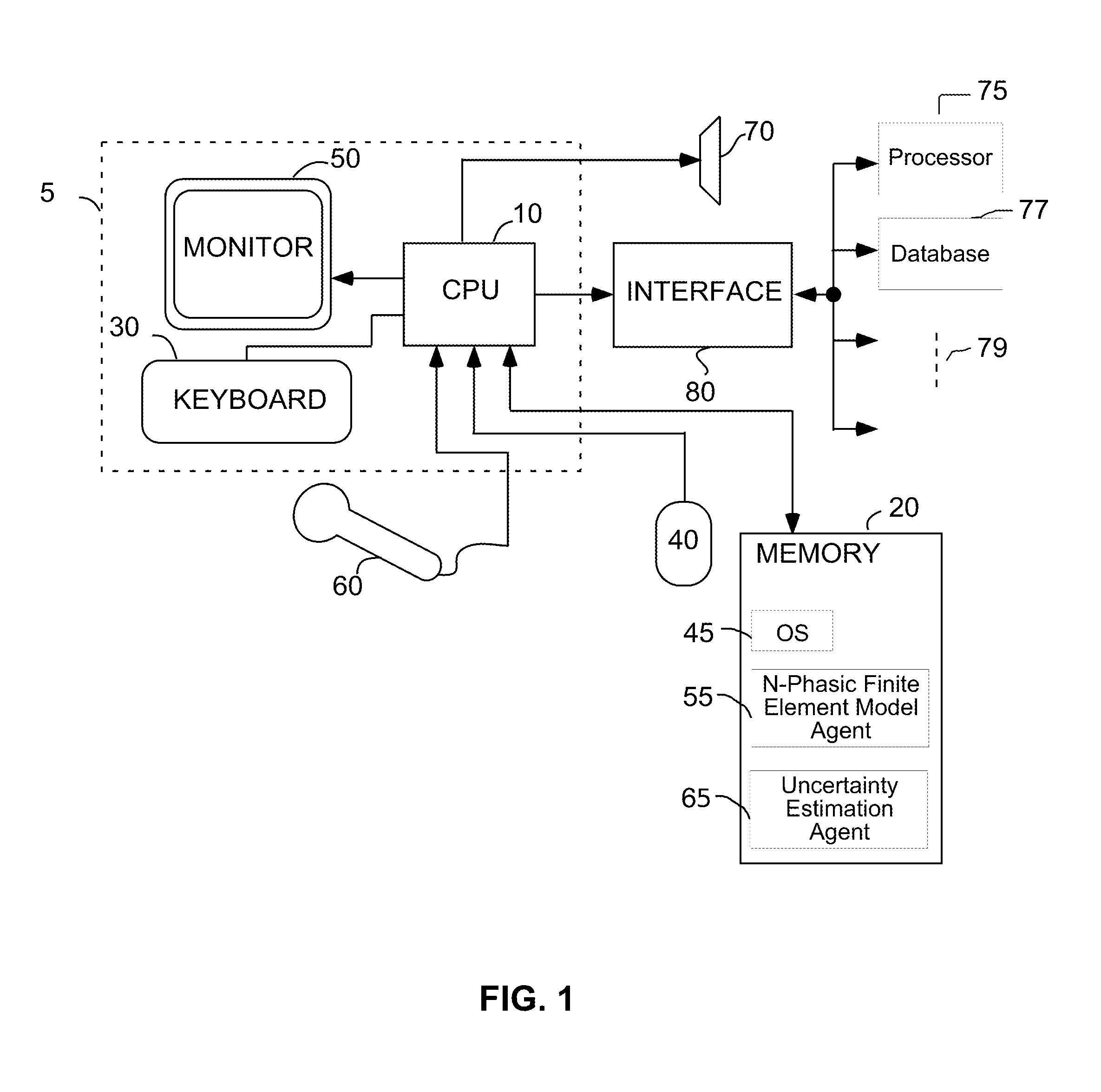
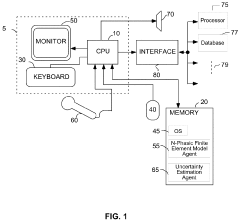
N-phasic element method for calculating a fully coupled response of multiphase compositional fluid flow and a system for uncertainty estimation
PatentActiveUS8255195B2
Innovation
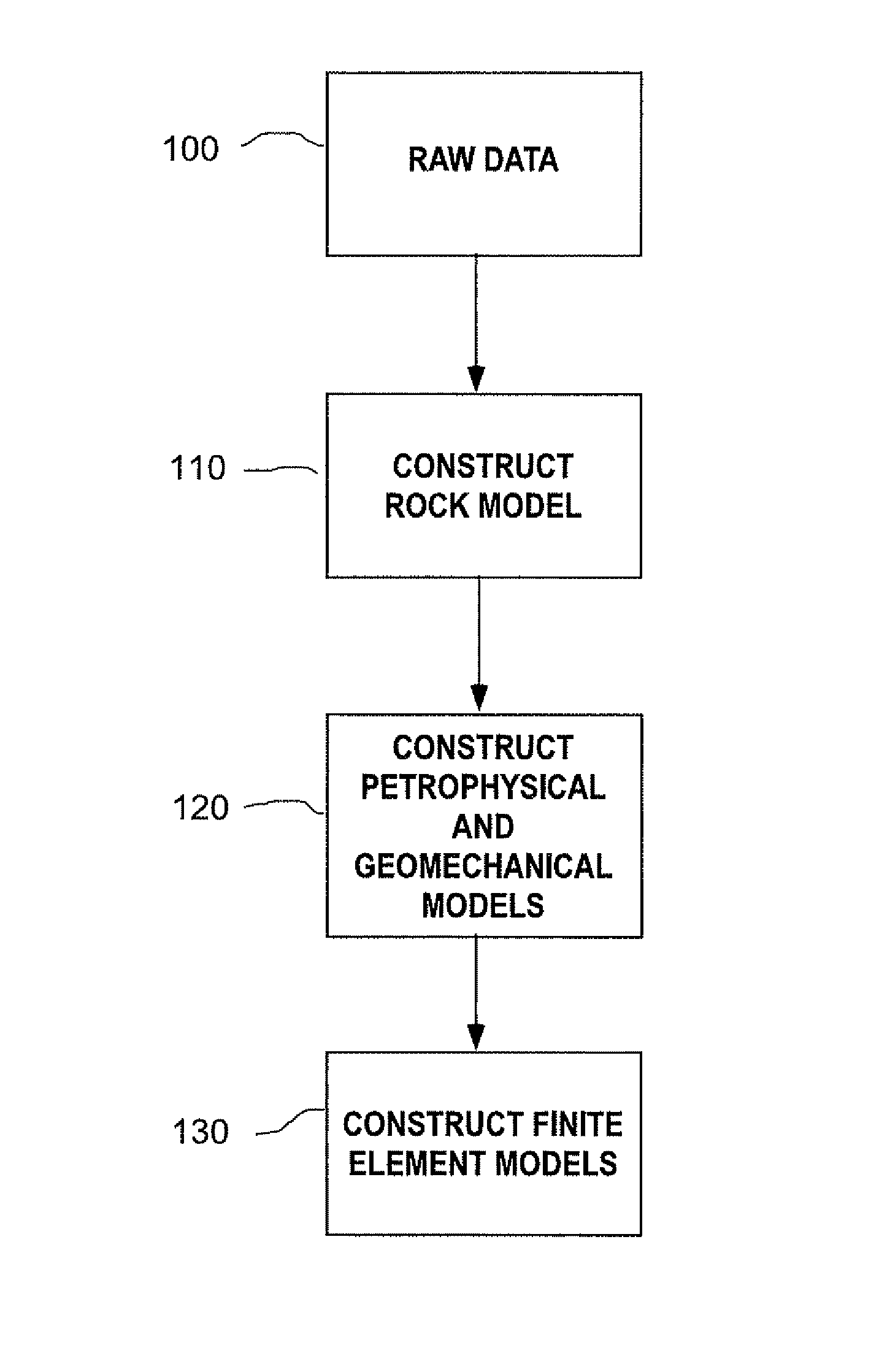
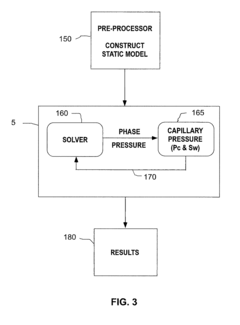
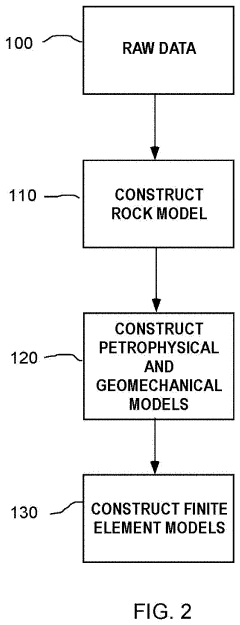
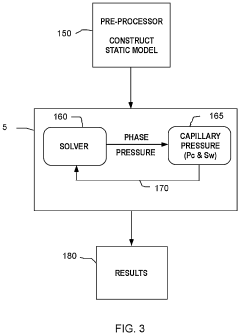
- A method using multi-grid finite element simulations, which involves collecting raw data, generating coarse or fine scale petrophysical and geomechanical models, and creating a multi-grid finite element simulation model to analyze subterranean formations, enabling the modeling of complex geometries and nonlinear behaviors.
N-phasic finite element method for calculating a fully coupled response of multiphase compositional fluid flow and a system for uncertainty estimation of the calculated reservoir response
PatentActiveUS10590762B2
Innovation
- A method and system for generating a multi-grid finite element simulation model of subterranean formations using raw data processing to create coarse or fine scale petrophysical and geomechanical property models, enabling fully coupled analysis of multi-phase compositional fluid flow and heat flow in nonlinearly deforming porous solid media with time-dependent failure, and estimating uncertainties in derived field solutions.
Computational Efficiency and Scalability Considerations
The computational demands of poromechanical finite element modeling present significant challenges for practical applications, particularly when dealing with large-scale, complex geological systems. Current implementations often struggle with performance bottlenecks that limit their applicability to real-world engineering problems requiring high resolution or extensive domains.
Performance optimization strategies have evolved considerably in recent years, with adaptive mesh refinement emerging as a critical technique. This approach dynamically allocates computational resources to regions with steep gradients or complex behavior while using coarser discretization elsewhere. Studies indicate that adaptive techniques can reduce computational costs by 40-60% compared to uniform mesh approaches without sacrificing accuracy in critical regions.
Parallel computing frameworks have revolutionized poromechanical simulations, with domain decomposition methods enabling efficient distribution of computational loads across multiple processors. Recent benchmarks demonstrate near-linear scaling up to thousands of cores for well-optimized codes. However, the communication overhead between subdomains remains a limiting factor, particularly for highly coupled problems where frequent data exchange is necessary.
Time-stepping strategies significantly impact both accuracy and efficiency. Implicit schemes offer stability advantages for the stiff differential equations characteristic of poromechanical problems but require solving large linear systems at each step. Explicit methods reduce computational cost per step but often necessitate prohibitively small time steps due to stability constraints. Advanced approaches like operator splitting and sequential coupling schemes attempt to balance these considerations.
Memory management presents another critical challenge, as high-resolution 3D simulations can easily exceed available RAM on standard computing systems. Out-of-core algorithms and GPU acceleration have emerged as promising solutions, with recent implementations demonstrating 5-10x performance improvements for certain problem classes.
Cloud computing and high-performance computing (HPC) infrastructures are increasingly essential for industrial-scale poromechanical simulations. The elasticity of cloud resources allows for dynamic scaling based on computational demands, though data transfer bottlenecks and licensing models for commercial software remain practical obstacles to widespread adoption.
Reduced-order modeling techniques offer promising alternatives for scenarios requiring numerous simulation runs, such as uncertainty quantification or optimization studies. By constructing computationally efficient surrogates based on full-physics simulations, these approaches can accelerate parametric studies by orders of magnitude, though careful validation remains essential to ensure accuracy.
Performance optimization strategies have evolved considerably in recent years, with adaptive mesh refinement emerging as a critical technique. This approach dynamically allocates computational resources to regions with steep gradients or complex behavior while using coarser discretization elsewhere. Studies indicate that adaptive techniques can reduce computational costs by 40-60% compared to uniform mesh approaches without sacrificing accuracy in critical regions.
Parallel computing frameworks have revolutionized poromechanical simulations, with domain decomposition methods enabling efficient distribution of computational loads across multiple processors. Recent benchmarks demonstrate near-linear scaling up to thousands of cores for well-optimized codes. However, the communication overhead between subdomains remains a limiting factor, particularly for highly coupled problems where frequent data exchange is necessary.
Time-stepping strategies significantly impact both accuracy and efficiency. Implicit schemes offer stability advantages for the stiff differential equations characteristic of poromechanical problems but require solving large linear systems at each step. Explicit methods reduce computational cost per step but often necessitate prohibitively small time steps due to stability constraints. Advanced approaches like operator splitting and sequential coupling schemes attempt to balance these considerations.
Memory management presents another critical challenge, as high-resolution 3D simulations can easily exceed available RAM on standard computing systems. Out-of-core algorithms and GPU acceleration have emerged as promising solutions, with recent implementations demonstrating 5-10x performance improvements for certain problem classes.
Cloud computing and high-performance computing (HPC) infrastructures are increasingly essential for industrial-scale poromechanical simulations. The elasticity of cloud resources allows for dynamic scaling based on computational demands, though data transfer bottlenecks and licensing models for commercial software remain practical obstacles to widespread adoption.
Reduced-order modeling techniques offer promising alternatives for scenarios requiring numerous simulation runs, such as uncertainty quantification or optimization studies. By constructing computationally efficient surrogates based on full-physics simulations, these approaches can accelerate parametric studies by orders of magnitude, though careful validation remains essential to ensure accuracy.
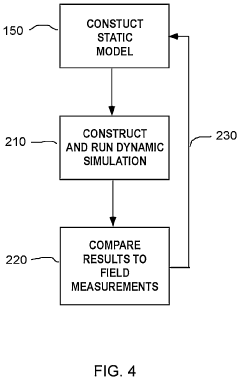
Validation Methodologies and Benchmark Problems
Validation of poromechanical finite element models requires rigorous methodologies to ensure accuracy and reliability in simulating coupled flow and deformation processes. The scientific community has established several standardized benchmark problems that serve as reference cases for validating numerical implementations. These benchmarks typically include analytical solutions for simplified geometries and loading conditions, allowing for direct comparison between numerical results and exact solutions.
The Terzaghi one-dimensional consolidation problem represents one of the most fundamental validation benchmarks in poromechanics. This classic problem examines the time-dependent dissipation of excess pore pressure under constant loading, providing a straightforward yet effective test for coupled hydro-mechanical implementations. Similarly, Mandel's problem, which considers a poroelastic rectangular domain subjected to compressive loading, introduces two-dimensional effects and the characteristic non-monotonic pore pressure response known as the Mandel-Cryer effect.
For more complex scenarios, the Cryer sphere problem examines radial consolidation in a spherical domain, while the Barry and Mercer problem addresses oscillatory loading conditions. These benchmarks collectively cover various aspects of poromechanical coupling, including transient responses, boundary conditions, and geometric configurations.
Beyond analytical solutions, validation methodologies increasingly incorporate laboratory experiments designed specifically for code verification. These experiments typically measure quantities such as displacement fields, pore pressure distributions, and fluid flux under controlled conditions. Advanced imaging techniques, including X-ray computed tomography and digital image correlation, have enhanced the precision of experimental validation data by providing spatially resolved measurements of deformation and fluid movement.
Inter-code comparison represents another crucial validation approach, where results from different numerical implementations are compared to identify potential implementation errors or numerical artifacts. International collaborative efforts, such as the DECOVALEX project for geomechanical applications, have established frameworks for systematic code comparison across multiple research groups.
Sensitivity analysis forms an essential component of validation methodologies, assessing how variations in input parameters affect simulation outcomes. This approach helps identify critical parameters requiring precise characterization and quantifies uncertainty propagation through the numerical model. Modern validation frameworks increasingly incorporate uncertainty quantification techniques, recognizing that both numerical models and experimental measurements contain inherent uncertainties that must be accounted for in meaningful comparisons.
The Terzaghi one-dimensional consolidation problem represents one of the most fundamental validation benchmarks in poromechanics. This classic problem examines the time-dependent dissipation of excess pore pressure under constant loading, providing a straightforward yet effective test for coupled hydro-mechanical implementations. Similarly, Mandel's problem, which considers a poroelastic rectangular domain subjected to compressive loading, introduces two-dimensional effects and the characteristic non-monotonic pore pressure response known as the Mandel-Cryer effect.
For more complex scenarios, the Cryer sphere problem examines radial consolidation in a spherical domain, while the Barry and Mercer problem addresses oscillatory loading conditions. These benchmarks collectively cover various aspects of poromechanical coupling, including transient responses, boundary conditions, and geometric configurations.
Beyond analytical solutions, validation methodologies increasingly incorporate laboratory experiments designed specifically for code verification. These experiments typically measure quantities such as displacement fields, pore pressure distributions, and fluid flux under controlled conditions. Advanced imaging techniques, including X-ray computed tomography and digital image correlation, have enhanced the precision of experimental validation data by providing spatially resolved measurements of deformation and fluid movement.
Inter-code comparison represents another crucial validation approach, where results from different numerical implementations are compared to identify potential implementation errors or numerical artifacts. International collaborative efforts, such as the DECOVALEX project for geomechanical applications, have established frameworks for systematic code comparison across multiple research groups.
Sensitivity analysis forms an essential component of validation methodologies, assessing how variations in input parameters affect simulation outcomes. This approach helps identify critical parameters requiring precise characterization and quantifies uncertainty propagation through the numerical model. Modern validation frameworks increasingly incorporate uncertainty quantification techniques, recognizing that both numerical models and experimental measurements contain inherent uncertainties that must be accounted for in meaningful comparisons.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!