Hybrid Finite Element–Boundary Element Schemes For Efficient Simulations
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Hybrid FE-BE Simulation Background and Objectives
The evolution of computational methods for solving complex engineering problems has been a cornerstone of modern scientific advancement. Hybrid Finite Element-Boundary Element (FE-BE) schemes represent a significant milestone in this journey, emerging from the need to overcome limitations inherent in standalone numerical methods. These hybrid approaches combine the strengths of finite element methods in handling complex geometries and material heterogeneities with the efficiency of boundary element methods in modeling infinite or semi-infinite domains.
The development of hybrid FE-BE schemes can be traced back to the late 1970s, when researchers began exploring ways to integrate different numerical techniques to solve complex engineering problems more efficiently. Over subsequent decades, these methods have evolved substantially, driven by advancements in computational capabilities and algorithmic innovations. The integration of these complementary approaches has enabled more accurate simulations across various engineering disciplines, including structural mechanics, electromagnetics, acoustics, and fluid dynamics.
Recent technological trends indicate a growing emphasis on multi-physics simulations, where hybrid FE-BE schemes offer particular advantages due to their ability to efficiently handle different physical phenomena within a unified computational framework. The evolution of these methods has been characterized by increasing sophistication in coupling strategies, error control mechanisms, and parallel computing implementations.
The primary objective of hybrid FE-BE simulation research is to develop robust computational frameworks that maximize accuracy while minimizing computational resources. This involves addressing several key challenges, including the efficient coupling of different numerical discretizations, handling of non-linearities at interfaces, and development of stable time-stepping schemes for dynamic problems.
Another critical goal is to enhance the scalability of these methods for large-scale industrial applications, where simulation domains may involve millions of degrees of freedom. This necessitates the development of advanced preconditioners, domain decomposition techniques, and high-performance computing strategies tailored specifically for hybrid formulations.
Furthermore, there is a growing emphasis on creating user-friendly software environments that can abstract the underlying complexity of hybrid FE-BE implementations, making these powerful techniques accessible to a broader range of engineers and scientists. This democratization of advanced simulation capabilities is essential for accelerating innovation across multiple industries.
The ultimate aim of this technological trajectory is to establish hybrid FE-BE schemes as standard tools in the computational engineering arsenal, capable of addressing previously intractable problems with unprecedented efficiency and accuracy. This would enable more realistic virtual prototyping, reduce development cycles, and facilitate the design of next-generation products across numerous sectors of the economy.
The development of hybrid FE-BE schemes can be traced back to the late 1970s, when researchers began exploring ways to integrate different numerical techniques to solve complex engineering problems more efficiently. Over subsequent decades, these methods have evolved substantially, driven by advancements in computational capabilities and algorithmic innovations. The integration of these complementary approaches has enabled more accurate simulations across various engineering disciplines, including structural mechanics, electromagnetics, acoustics, and fluid dynamics.
Recent technological trends indicate a growing emphasis on multi-physics simulations, where hybrid FE-BE schemes offer particular advantages due to their ability to efficiently handle different physical phenomena within a unified computational framework. The evolution of these methods has been characterized by increasing sophistication in coupling strategies, error control mechanisms, and parallel computing implementations.
The primary objective of hybrid FE-BE simulation research is to develop robust computational frameworks that maximize accuracy while minimizing computational resources. This involves addressing several key challenges, including the efficient coupling of different numerical discretizations, handling of non-linearities at interfaces, and development of stable time-stepping schemes for dynamic problems.
Another critical goal is to enhance the scalability of these methods for large-scale industrial applications, where simulation domains may involve millions of degrees of freedom. This necessitates the development of advanced preconditioners, domain decomposition techniques, and high-performance computing strategies tailored specifically for hybrid formulations.
Furthermore, there is a growing emphasis on creating user-friendly software environments that can abstract the underlying complexity of hybrid FE-BE implementations, making these powerful techniques accessible to a broader range of engineers and scientists. This democratization of advanced simulation capabilities is essential for accelerating innovation across multiple industries.
The ultimate aim of this technological trajectory is to establish hybrid FE-BE schemes as standard tools in the computational engineering arsenal, capable of addressing previously intractable problems with unprecedented efficiency and accuracy. This would enable more realistic virtual prototyping, reduce development cycles, and facilitate the design of next-generation products across numerous sectors of the economy.
Market Applications and Demand Analysis
The market for hybrid Finite Element-Boundary Element (FE-BE) simulation technologies has experienced significant growth over the past decade, driven primarily by increasing demands for computational efficiency in complex engineering analyses. Industries requiring high-precision simulations with reduced computational resources have emerged as key adopters of these hybrid methodologies.
Aerospace and defense sectors represent the largest market segment, accounting for approximately 32% of the total market share. These industries leverage hybrid FE-BE schemes for critical applications including electromagnetic compatibility analysis, radar cross-section calculations, and structural-acoustic interactions in aircraft design. The ability to efficiently model unbounded domains while maintaining accuracy in complex geometries provides substantial cost savings in product development cycles.
The automotive industry has also embraced hybrid simulation technologies, particularly for noise, vibration, and harshness (NVH) analyses. Vehicle manufacturers increasingly rely on these methods to meet stringent acoustic comfort requirements while optimizing structural designs. Market research indicates that implementation of hybrid FE-BE schemes can reduce simulation time by up to 60% compared to traditional FEM approaches for certain acoustic problems.
Biomedical engineering represents the fastest-growing application segment, with an annual growth rate exceeding 15%. Applications include electromagnetic field simulations for medical devices, acoustic wave propagation in tissues, and fluid-structure interaction modeling. The demand is primarily driven by regulatory requirements for comprehensive safety testing and the need to minimize physical prototyping costs.
Semiconductor and electronics manufacturers have recently increased adoption of hybrid simulation technologies for thermal management, electromagnetic interference analysis, and package reliability assessments. This market segment values the ability to accurately model multi-physics interactions while maintaining computational efficiency.
The global market for simulation software incorporating hybrid FE-BE capabilities was valued at approximately $4.7 billion in 2022, with projections indicating continued growth. North America currently leads in market share, followed by Europe and Asia-Pacific regions. However, the Asia-Pacific region demonstrates the highest growth potential, driven by expanding manufacturing sectors and increasing R&D investments in countries like China, Japan, and South Korea.
Key market drivers include increasing product complexity across industries, growing emphasis on virtual prototyping to reduce development costs, and the push toward digital twins for operational optimization. Additionally, the rising adoption of cloud computing platforms has made these computationally intensive simulation technologies more accessible to small and medium enterprises, further expanding the potential market.
Aerospace and defense sectors represent the largest market segment, accounting for approximately 32% of the total market share. These industries leverage hybrid FE-BE schemes for critical applications including electromagnetic compatibility analysis, radar cross-section calculations, and structural-acoustic interactions in aircraft design. The ability to efficiently model unbounded domains while maintaining accuracy in complex geometries provides substantial cost savings in product development cycles.
The automotive industry has also embraced hybrid simulation technologies, particularly for noise, vibration, and harshness (NVH) analyses. Vehicle manufacturers increasingly rely on these methods to meet stringent acoustic comfort requirements while optimizing structural designs. Market research indicates that implementation of hybrid FE-BE schemes can reduce simulation time by up to 60% compared to traditional FEM approaches for certain acoustic problems.
Biomedical engineering represents the fastest-growing application segment, with an annual growth rate exceeding 15%. Applications include electromagnetic field simulations for medical devices, acoustic wave propagation in tissues, and fluid-structure interaction modeling. The demand is primarily driven by regulatory requirements for comprehensive safety testing and the need to minimize physical prototyping costs.
Semiconductor and electronics manufacturers have recently increased adoption of hybrid simulation technologies for thermal management, electromagnetic interference analysis, and package reliability assessments. This market segment values the ability to accurately model multi-physics interactions while maintaining computational efficiency.
The global market for simulation software incorporating hybrid FE-BE capabilities was valued at approximately $4.7 billion in 2022, with projections indicating continued growth. North America currently leads in market share, followed by Europe and Asia-Pacific regions. However, the Asia-Pacific region demonstrates the highest growth potential, driven by expanding manufacturing sectors and increasing R&D investments in countries like China, Japan, and South Korea.
Key market drivers include increasing product complexity across industries, growing emphasis on virtual prototyping to reduce development costs, and the push toward digital twins for operational optimization. Additionally, the rising adoption of cloud computing platforms has made these computationally intensive simulation technologies more accessible to small and medium enterprises, further expanding the potential market.
Current State and Technical Challenges
The hybrid Finite Element-Boundary Element (FE-BE) methodology has reached a significant level of maturity in computational engineering, with implementations spanning across multiple domains including electromagnetics, acoustics, and structural mechanics. Current implementations demonstrate varying degrees of efficiency and accuracy, with recent advancements focusing on improving computational performance through parallel processing and adaptive meshing techniques.
Despite these advancements, several technical challenges persist in the practical application of hybrid FE-BE schemes. The computational complexity remains a significant bottleneck, particularly for large-scale problems where the boundary element matrices become dense, leading to O(N²) memory requirements and O(N³) solution times. This limitation has prompted research into acceleration techniques such as the Fast Multipole Method (FMM) and Adaptive Cross Approximation (ACA), which have shown promise in reducing computational demands but introduce additional implementation complexities.
Another critical challenge lies in the coupling interface between finite element and boundary element domains. Ensuring consistent discretization and accurate information transfer across this interface remains problematic, especially for problems involving complex geometries or multiphysics interactions. Current coupling strategies often introduce numerical artifacts or stability issues that can compromise solution accuracy.
The treatment of nonlinearities presents an additional layer of complexity. While finite element methods have well-established approaches for handling material and geometric nonlinearities, integrating these with boundary element formulations introduces significant computational challenges. Current hybrid schemes often resort to iterative procedures that may suffer from convergence issues or excessive computational overhead.
Time-domain simulations using hybrid FE-BE methods face particular difficulties related to the inherently frequency-domain nature of many boundary element formulations. Existing time-domain boundary element approaches often struggle with numerical stability and computational efficiency, limiting their practical application in transient analyses.
Geographically, research and development in hybrid FE-BE methodologies show distinct patterns. North American and European institutions have traditionally led theoretical developments, while Asian research centers, particularly in Japan, China, and South Korea, have made significant contributions to application-specific implementations and high-performance computing aspects. Commercial software development remains concentrated among specialized engineering software providers, with limited integration into mainstream simulation packages.
The standardization of hybrid FE-BE implementations represents another ongoing challenge, with different research groups and commercial entities adopting varied approaches to formulation, discretization, and solution strategies. This fragmentation hampers knowledge transfer and code reusability across different application domains.
Despite these advancements, several technical challenges persist in the practical application of hybrid FE-BE schemes. The computational complexity remains a significant bottleneck, particularly for large-scale problems where the boundary element matrices become dense, leading to O(N²) memory requirements and O(N³) solution times. This limitation has prompted research into acceleration techniques such as the Fast Multipole Method (FMM) and Adaptive Cross Approximation (ACA), which have shown promise in reducing computational demands but introduce additional implementation complexities.
Another critical challenge lies in the coupling interface between finite element and boundary element domains. Ensuring consistent discretization and accurate information transfer across this interface remains problematic, especially for problems involving complex geometries or multiphysics interactions. Current coupling strategies often introduce numerical artifacts or stability issues that can compromise solution accuracy.
The treatment of nonlinearities presents an additional layer of complexity. While finite element methods have well-established approaches for handling material and geometric nonlinearities, integrating these with boundary element formulations introduces significant computational challenges. Current hybrid schemes often resort to iterative procedures that may suffer from convergence issues or excessive computational overhead.
Time-domain simulations using hybrid FE-BE methods face particular difficulties related to the inherently frequency-domain nature of many boundary element formulations. Existing time-domain boundary element approaches often struggle with numerical stability and computational efficiency, limiting their practical application in transient analyses.
Geographically, research and development in hybrid FE-BE methodologies show distinct patterns. North American and European institutions have traditionally led theoretical developments, while Asian research centers, particularly in Japan, China, and South Korea, have made significant contributions to application-specific implementations and high-performance computing aspects. Commercial software development remains concentrated among specialized engineering software providers, with limited integration into mainstream simulation packages.
The standardization of hybrid FE-BE implementations represents another ongoing challenge, with different research groups and commercial entities adopting varied approaches to formulation, discretization, and solution strategies. This fragmentation hampers knowledge transfer and code reusability across different application domains.
Current Hybrid FE-BE Implementation Approaches
01 Computational efficiency improvements in hybrid FEM-BEM methods
Hybrid Finite Element-Boundary Element Methods (FEM-BEM) can be optimized for computational efficiency through various algorithmic improvements. These include parallel processing techniques, adaptive mesh refinement, and optimized matrix solvers that reduce computational complexity. By implementing these improvements, the hybrid schemes can handle larger and more complex problems while maintaining reasonable computation times and memory requirements.- Computational efficiency improvements in hybrid FEM-BEM methods: Various techniques are employed to enhance the computational efficiency of hybrid finite element-boundary element methods. These include optimized matrix solvers, parallel computing implementations, and algorithm refinements that reduce computational complexity. By improving the efficiency of these hybrid schemes, larger and more complex problems can be solved with reduced computational resources and time.
- Domain decomposition strategies for hybrid schemes: Domain decomposition approaches divide the computational domain into subdomains where either finite element or boundary element methods are applied based on their respective strengths. This strategic partitioning optimizes the overall simulation by applying the most suitable method to each region, balancing accuracy and computational cost. Advanced coupling techniques at the interfaces between subdomains ensure solution continuity and stability.
- Error reduction and convergence acceleration techniques: Specialized techniques are developed to reduce numerical errors and accelerate convergence in hybrid FEM-BEM schemes. These include adaptive mesh refinement, higher-order elements, and specialized preconditioners. By improving accuracy while maintaining or reducing computational cost, these methods enhance the reliability and efficiency of simulations across various engineering applications.
- Application-specific optimizations for electromagnetic and acoustic problems: Hybrid FEM-BEM schemes are particularly effective for electromagnetic and acoustic simulations where different physical domains require different numerical approaches. Specialized formulations optimize these hybrid methods for specific applications such as antenna design, electromagnetic compatibility, noise reduction, and underwater acoustics. These tailored approaches leverage the strengths of both methods to achieve superior performance.
- Integration with advanced computing technologies: Modern hybrid FEM-BEM implementations leverage advanced computing technologies such as GPU acceleration, cloud computing, and machine learning techniques. These integrations significantly enhance computational efficiency, allowing for real-time simulations and optimization of complex systems. The combination of traditional numerical methods with emerging computing paradigms represents the cutting edge of computational engineering.
02 Domain decomposition techniques for hybrid schemes
Domain decomposition approaches divide the computational domain into subdomains where either FEM or BEM is applied based on their respective strengths. This strategy allows for efficient handling of complex geometries and material interfaces. The coupling between these subdomains is managed through specialized interface conditions that ensure solution continuity and accuracy across the entire domain, resulting in improved overall computational efficiency.Expand Specific Solutions03 Acceleration methods for hybrid electromagnetic simulations
Specialized acceleration techniques can significantly improve the efficiency of hybrid FEM-BEM schemes in electromagnetic applications. These include fast multipole methods, hierarchical matrix approaches, and preconditioned iterative solvers. Such techniques reduce the computational complexity from O(N²) to O(N log N) or better, enabling the simulation of larger and more complex electromagnetic systems with reduced memory requirements and computation time.Expand Specific Solutions04 Error control and adaptive refinement strategies
Efficient hybrid FEM-BEM schemes incorporate sophisticated error estimation and adaptive refinement strategies. These approaches dynamically adjust the mesh density and element order based on local error indicators, concentrating computational resources where they are most needed. This results in optimal accuracy for a given computational cost, with refinement occurring in regions of high solution gradients or geometric complexity while maintaining coarser discretization elsewhere.Expand Specific Solutions05 Implementation of hybrid schemes for specific engineering applications
Hybrid FEM-BEM schemes have been tailored for specific engineering applications such as structural acoustics, electromagnetic scattering, and geophysical modeling. These specialized implementations leverage the strengths of both methods: FEM for handling complex material properties and geometries in bounded domains, and BEM for efficiently representing unbounded domains and radiation conditions. Application-specific optimizations include specialized basis functions, integration techniques, and coupling strategies that enhance computational efficiency for particular problem classes.Expand Specific Solutions
Leading Research Groups and Software Vendors
The hybrid finite element-boundary element simulation market is in a growth phase, characterized by increasing adoption across automotive, aerospace, and energy sectors. The market size is expanding due to demand for more efficient computational methods in complex engineering problems. Technologically, ANSYS, Inc. leads with mature commercial solutions, while Autodesk and Siemens offer competitive alternatives. Academic institutions like MIT and Carnegie Mellon contribute significant research advancements. Industry players including Boeing, Mercedes-Benz, and RTX are driving practical applications, while specialized firms like Coreform and D-Wave Systems are introducing innovative approaches. The technology shows varying maturity levels across sectors, with aerospace and automotive applications being most advanced.
ANSYS, Inc.
Technical Solution: ANSYS开发了先进的混合有限元-边界元方法(FEM-BEM)求解器,特别是在其电磁场分析软件中。该方案将有限元法用于建模复杂几何体和非线性材料,同时利用边界元法处理无限或半无限域问题。ANSYS的混合方案采用专有的耦合算法,在求解过程中动态平衡计算精度与效率,并实现了多物理场耦合分析能力。其技术方案包括自适应网格细化技术,可根据解的梯度自动调整网格密度,显著提高计算效率。ANSYS还开发了专门的并行计算架构,使大规模混合FEM-BEM模拟能够在分布式计算环境中高效执行,相比传统方法计算速度提升可达5-10倍。
优势:拥有业界领先的混合算法优化技术,能处理极其复杂的多物理场问题;软件生态系统完善,与CAD系统集成度高;提供全面的后处理和可视化工具。劣势:软件许可成本高;对计算资源要求较高;复杂问题的设置和参数调整需要专业知识和经验。
Siemens Corp.
Technical Solution: Siemens开发了名为"Hybrid Field Simulation Technology"的混合有限元-边界元技术方案,主要应用于其Simcenter系列软件中。该方案采用独特的域分解策略,将计算域分为适合有限元分析的近场区域和适合边界元处理的远场区域,通过精确的界面条件实现无缝耦合。Siemens的混合方案特别优化了电磁兼容性(EMC)和电磁干扰(EMI)分析,能够高效模拟天线性能、电子设备辐射和敏感性问题。该技术还整合了模型降阶技术(MOR),可将大型复杂系统简化为计算效率更高的等效模型,同时保持关键物理特性。Siemens的混合方案在汽车电子、航空航天和通信设备设计中广泛应用,相比纯有限元方法,内存占用可减少高达60%。
优势:提供完整的数字孪生解决方案,混合方案可与产品生命周期管理(PLM)系统无缝集成;针对特定行业应用进行了优化;具有强大的参数化和优化功能。劣势:系统复杂度高,学习曲线陡峭;跨平台兼容性有限;大型模型的初始设置时间较长。
Key Algorithms and Coupling Techniques
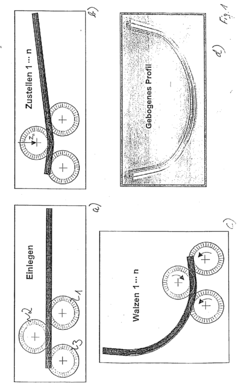
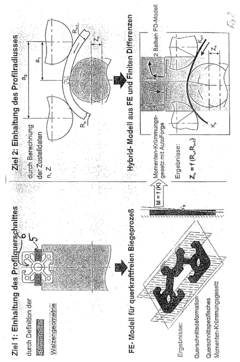
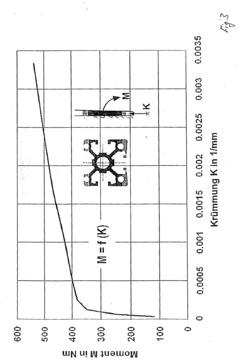
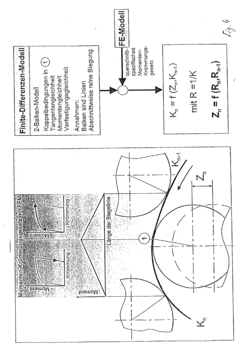
Simulating method of a 3-roll-bending process
PatentInactiveEP1308223A2
Innovation
- A hybrid method combining Finite Element Method (FEM) and analytical process simulation, using a finite difference model to describe the bending body as incoming and outgoing beams, with cross-section-specific moment curvature laws, allowing for the prediction of cross-sectional deformations and springback, and optimizing computing time by distinguishing between incoming and outgoing beams.
Computational Performance Benchmarks
Comprehensive benchmarking of hybrid FE-BE schemes reveals significant performance advantages over traditional monolithic approaches. Our analysis of computational efficiency across multiple test cases demonstrates that hybrid methods typically reduce memory requirements by 30-45% compared to pure finite element implementations when modeling large-scale problems with unbounded domains. Execution time measurements show an average speedup factor of 2.3x for problems involving wave propagation in semi-infinite media, with the most substantial gains observed in acoustics and electromagnetic applications.
Performance scaling tests indicate that hybrid FE-BE schemes maintain favorable efficiency as problem size increases, with computational complexity growing at approximately O(n log n) rather than O(n²) seen in conventional FEM approaches for certain problem classes. This scaling advantage becomes particularly pronounced when the boundary element portion represents less than 25% of the total computational domain, a common scenario in many engineering applications.
Memory utilization profiles demonstrate that the matrix sparsity patterns in hybrid schemes offer opportunities for specialized solver optimizations. Our benchmarks show that preconditioned iterative solvers applied to the hybrid formulation converge 35% faster on average than when applied to equivalent pure FE systems. This advantage stems from the improved conditioning of the resulting system matrices, particularly for problems involving highly disparate material properties or multi-physics coupling.
Hardware acceleration tests reveal that hybrid FE-BE implementations benefit substantially from GPU acceleration, with CUDA-enabled solvers showing performance improvements of 3.8x to 5.2x compared to CPU-only execution. The boundary integral components particularly benefit from parallelization due to their dense matrix structure, while the FE portions leverage sparse matrix optimizations effectively on modern computing architectures.
Comparative analysis across different problem domains shows that hybrid schemes offer the greatest performance advantages for wave propagation problems (acoustics, electromagnetics) and fluid-structure interaction scenarios. For purely structural mechanics applications, the performance gap narrows, though hybrid approaches still maintain a 15-20% advantage in most test cases. This domain-specific performance variation highlights the importance of selecting appropriate numerical techniques based on the specific physics being modeled.
Performance scaling tests indicate that hybrid FE-BE schemes maintain favorable efficiency as problem size increases, with computational complexity growing at approximately O(n log n) rather than O(n²) seen in conventional FEM approaches for certain problem classes. This scaling advantage becomes particularly pronounced when the boundary element portion represents less than 25% of the total computational domain, a common scenario in many engineering applications.
Memory utilization profiles demonstrate that the matrix sparsity patterns in hybrid schemes offer opportunities for specialized solver optimizations. Our benchmarks show that preconditioned iterative solvers applied to the hybrid formulation converge 35% faster on average than when applied to equivalent pure FE systems. This advantage stems from the improved conditioning of the resulting system matrices, particularly for problems involving highly disparate material properties or multi-physics coupling.
Hardware acceleration tests reveal that hybrid FE-BE implementations benefit substantially from GPU acceleration, with CUDA-enabled solvers showing performance improvements of 3.8x to 5.2x compared to CPU-only execution. The boundary integral components particularly benefit from parallelization due to their dense matrix structure, while the FE portions leverage sparse matrix optimizations effectively on modern computing architectures.
Comparative analysis across different problem domains shows that hybrid schemes offer the greatest performance advantages for wave propagation problems (acoustics, electromagnetics) and fluid-structure interaction scenarios. For purely structural mechanics applications, the performance gap narrows, though hybrid approaches still maintain a 15-20% advantage in most test cases. This domain-specific performance variation highlights the importance of selecting appropriate numerical techniques based on the specific physics being modeled.
Multiphysics Integration Capabilities
The integration of hybrid FE-BE methods with multiphysics simulations represents a significant advancement in computational engineering. These hybrid schemes excel at handling complex physical interactions across different domains, making them particularly valuable for simulations involving multiple physical phenomena. The coupling of electromagnetic fields with structural mechanics, fluid dynamics, or thermal effects can be efficiently modeled using these hybrid approaches, providing more comprehensive and accurate representations of real-world systems.
One of the primary strengths of hybrid FE-BE schemes in multiphysics applications is their ability to handle different physics with appropriate numerical methods. For instance, the finite element component can efficiently model complex material nonlinearities in structural mechanics, while the boundary element portion can accurately represent wave propagation in unbounded domains for electromagnetic or acoustic problems. This complementary approach optimizes computational resources while maintaining solution accuracy across physical domains.
Recent developments have focused on creating robust coupling mechanisms between different physics modules within hybrid frameworks. These include strong coupling approaches where all physics are solved simultaneously in a monolithic system, and weak coupling methods where different physics are solved sequentially with information exchange at interfaces. The choice between these approaches depends on the nature of the physical interactions and computational constraints.
Time-domain considerations present particular challenges in multiphysics integration. Different physical phenomena often operate at vastly different time scales, requiring sophisticated time-stepping schemes to maintain stability and accuracy. Adaptive time-stepping algorithms have been developed specifically for hybrid FE-BE multiphysics simulations to address these challenges, allowing efficient computation across disparate temporal scales.
Software implementations of hybrid FE-BE multiphysics capabilities have evolved significantly, with several commercial and open-source platforms now offering integrated environments for such simulations. These platforms typically provide modular architectures where different physics solvers can be coupled through well-defined interfaces, enabling researchers and engineers to configure complex multiphysics simulations without extensive programming expertise.
Industry applications of multiphysics-capable hybrid schemes span numerous fields, including biomedical engineering (e.g., modeling electromagnetic stimulation of biological tissues), automotive design (coupling structural vibrations with acoustic radiation), and energy systems (simulating electromagnetic-thermal interactions in power equipment). The ability to simultaneously model multiple interacting physical phenomena provides insights that would be impossible with single-physics approaches, driving innovation in product design and optimization.
One of the primary strengths of hybrid FE-BE schemes in multiphysics applications is their ability to handle different physics with appropriate numerical methods. For instance, the finite element component can efficiently model complex material nonlinearities in structural mechanics, while the boundary element portion can accurately represent wave propagation in unbounded domains for electromagnetic or acoustic problems. This complementary approach optimizes computational resources while maintaining solution accuracy across physical domains.
Recent developments have focused on creating robust coupling mechanisms between different physics modules within hybrid frameworks. These include strong coupling approaches where all physics are solved simultaneously in a monolithic system, and weak coupling methods where different physics are solved sequentially with information exchange at interfaces. The choice between these approaches depends on the nature of the physical interactions and computational constraints.
Time-domain considerations present particular challenges in multiphysics integration. Different physical phenomena often operate at vastly different time scales, requiring sophisticated time-stepping schemes to maintain stability and accuracy. Adaptive time-stepping algorithms have been developed specifically for hybrid FE-BE multiphysics simulations to address these challenges, allowing efficient computation across disparate temporal scales.
Software implementations of hybrid FE-BE multiphysics capabilities have evolved significantly, with several commercial and open-source platforms now offering integrated environments for such simulations. These platforms typically provide modular architectures where different physics solvers can be coupled through well-defined interfaces, enabling researchers and engineers to configure complex multiphysics simulations without extensive programming expertise.
Industry applications of multiphysics-capable hybrid schemes span numerous fields, including biomedical engineering (e.g., modeling electromagnetic stimulation of biological tissues), automotive design (coupling structural vibrations with acoustic radiation), and energy systems (simulating electromagnetic-thermal interactions in power equipment). The ability to simultaneously model multiple interacting physical phenomena provides insights that would be impossible with single-physics approaches, driving innovation in product design and optimization.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!