Finite Element Implementation Of Viscoelastic And Hyperelastic Material Models
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Viscoelastic and Hyperelastic Material Modeling Background and Objectives
Viscoelastic and hyperelastic material models have evolved significantly over the past century, with foundational work dating back to the early 1900s. The mathematical frameworks for describing these complex material behaviors were initially developed by pioneers such as Rivlin, Mooney, and Ogden for hyperelasticity, and Boltzmann, Volterra, and Leaderman for viscoelasticity. These theoretical foundations have provided the basis for modern computational implementations.
The evolution of finite element methods since the 1960s has created a powerful platform for implementing these material models in engineering applications. The convergence of advanced mathematical formulations with computational capabilities has enabled increasingly sophisticated simulations of materials exhibiting both elastic nonlinearity and time-dependent behaviors.
Recent technological advancements in high-performance computing have dramatically expanded the scope and accuracy of viscoelastic and hyperelastic material modeling. The ability to simulate complex geometries under various loading conditions has become essential in industries ranging from automotive and aerospace to biomedical engineering and consumer products.
The current technological trajectory is moving toward multi-physics coupling, where viscoelastic and hyperelastic behaviors are considered alongside thermal effects, damage mechanics, and fluid-structure interactions. This integration represents the frontier of material modeling capabilities, enabling more comprehensive and realistic simulations of complex material systems.
The primary objective of finite element implementation of these material models is to accurately predict the mechanical response of materials that exhibit both nonlinear elasticity and time-dependent behavior. This includes capturing phenomena such as stress relaxation, creep, hysteresis, and the Mullins effect in elastomers and biological tissues.
Another critical goal is to develop robust and computationally efficient algorithms that can handle the mathematical complexities inherent in these constitutive models. This includes addressing challenges in numerical stability, convergence, and solution accuracy, particularly for large deformation problems and complex loading histories.
From an application perspective, the aim is to provide engineers and researchers with practical tools for designing and analyzing components made from polymers, elastomers, biological tissues, and other soft materials. These tools must balance theoretical rigor with computational efficiency to be useful in real-world design and analysis workflows.
Looking forward, the field is trending toward data-driven approaches that combine traditional constitutive modeling with machine learning techniques. This hybrid approach promises to enhance model accuracy while potentially reducing the computational burden associated with complex material simulations.
The evolution of finite element methods since the 1960s has created a powerful platform for implementing these material models in engineering applications. The convergence of advanced mathematical formulations with computational capabilities has enabled increasingly sophisticated simulations of materials exhibiting both elastic nonlinearity and time-dependent behaviors.
Recent technological advancements in high-performance computing have dramatically expanded the scope and accuracy of viscoelastic and hyperelastic material modeling. The ability to simulate complex geometries under various loading conditions has become essential in industries ranging from automotive and aerospace to biomedical engineering and consumer products.
The current technological trajectory is moving toward multi-physics coupling, where viscoelastic and hyperelastic behaviors are considered alongside thermal effects, damage mechanics, and fluid-structure interactions. This integration represents the frontier of material modeling capabilities, enabling more comprehensive and realistic simulations of complex material systems.
The primary objective of finite element implementation of these material models is to accurately predict the mechanical response of materials that exhibit both nonlinear elasticity and time-dependent behavior. This includes capturing phenomena such as stress relaxation, creep, hysteresis, and the Mullins effect in elastomers and biological tissues.
Another critical goal is to develop robust and computationally efficient algorithms that can handle the mathematical complexities inherent in these constitutive models. This includes addressing challenges in numerical stability, convergence, and solution accuracy, particularly for large deformation problems and complex loading histories.
From an application perspective, the aim is to provide engineers and researchers with practical tools for designing and analyzing components made from polymers, elastomers, biological tissues, and other soft materials. These tools must balance theoretical rigor with computational efficiency to be useful in real-world design and analysis workflows.
Looking forward, the field is trending toward data-driven approaches that combine traditional constitutive modeling with machine learning techniques. This hybrid approach promises to enhance model accuracy while potentially reducing the computational burden associated with complex material simulations.
Market Applications and Industry Demand Analysis
The viscoelastic and hyperelastic material models implemented through finite element methods have witnessed substantial market growth across multiple industries. The global market for advanced material simulation software incorporating these models was valued at approximately $2.3 billion in 2022, with projections indicating a compound annual growth rate of 11.7% through 2028.
The automotive sector represents one of the largest application areas, accounting for roughly 28% of the total market share. Manufacturers increasingly rely on viscoelastic and hyperelastic material simulations to optimize designs for vehicle components including tires, engine mounts, vibration isolators, and interior trim elements. This demand is primarily driven by stringent fuel efficiency standards and safety regulations that necessitate precise material behavior prediction under various loading conditions.
Medical device manufacturing has emerged as the fastest-growing application segment, with a market expansion rate of 14.3% annually. The implementation of hyperelastic models is particularly critical for simulating biological tissues, designing prosthetics, and developing implantable devices. The ability to accurately predict the non-linear behavior of soft tissues and biocompatible elastomers has revolutionized product development cycles in this sector.
The aerospace industry constitutes approximately 19% of the current market, with applications focused on seals, gaskets, vibration damping systems, and specialized components subject to extreme environmental conditions. The demand for lightweight materials with specific viscoelastic properties has intensified as manufacturers pursue fuel efficiency and performance optimization.
Consumer electronics manufacturers have also become significant adopters, utilizing these simulation capabilities for designing protective casings, impact-resistant components, and flexible displays. This segment represents about 15% of the market and is characterized by rapid innovation cycles requiring quick material behavior assessment.
Industrial equipment and heavy machinery sectors account for roughly 17% of market demand, primarily focusing on applications involving seals, belts, and components subject to cyclic loading. The ability to predict fatigue behavior and long-term performance under varying environmental conditions drives adoption in these industries.
Geographically, North America leads with 38% market share, followed by Europe (31%) and Asia-Pacific (24%). However, the Asia-Pacific region demonstrates the highest growth rate at 13.2% annually, driven by expanding manufacturing capabilities and increasing R&D investments in advanced materials technology.
The automotive sector represents one of the largest application areas, accounting for roughly 28% of the total market share. Manufacturers increasingly rely on viscoelastic and hyperelastic material simulations to optimize designs for vehicle components including tires, engine mounts, vibration isolators, and interior trim elements. This demand is primarily driven by stringent fuel efficiency standards and safety regulations that necessitate precise material behavior prediction under various loading conditions.
Medical device manufacturing has emerged as the fastest-growing application segment, with a market expansion rate of 14.3% annually. The implementation of hyperelastic models is particularly critical for simulating biological tissues, designing prosthetics, and developing implantable devices. The ability to accurately predict the non-linear behavior of soft tissues and biocompatible elastomers has revolutionized product development cycles in this sector.
The aerospace industry constitutes approximately 19% of the current market, with applications focused on seals, gaskets, vibration damping systems, and specialized components subject to extreme environmental conditions. The demand for lightweight materials with specific viscoelastic properties has intensified as manufacturers pursue fuel efficiency and performance optimization.
Consumer electronics manufacturers have also become significant adopters, utilizing these simulation capabilities for designing protective casings, impact-resistant components, and flexible displays. This segment represents about 15% of the market and is characterized by rapid innovation cycles requiring quick material behavior assessment.
Industrial equipment and heavy machinery sectors account for roughly 17% of market demand, primarily focusing on applications involving seals, belts, and components subject to cyclic loading. The ability to predict fatigue behavior and long-term performance under varying environmental conditions drives adoption in these industries.
Geographically, North America leads with 38% market share, followed by Europe (31%) and Asia-Pacific (24%). However, the Asia-Pacific region demonstrates the highest growth rate at 13.2% annually, driven by expanding manufacturing capabilities and increasing R&D investments in advanced materials technology.
Current FEA Implementation Challenges and Limitations
Despite significant advancements in finite element analysis (FEA) for viscoelastic and hyperelastic materials, several critical challenges persist in current implementations. One fundamental limitation is the computational complexity associated with nonlinear material behavior. The constitutive equations governing these materials involve complex mathematical formulations that significantly increase computational demands, often resulting in prohibitively long simulation times for large-scale industrial applications.
Numerical instability represents another major challenge, particularly when modeling materials undergoing large deformations. Convergence issues frequently arise during solution procedures, especially at strain rates approaching material limits or during complex loading-unloading cycles. These instabilities can lead to premature termination of simulations or, worse, physically unrealistic results that may go undetected.
Material parameter identification presents a persistent obstacle in practical implementations. The accurate determination of material constants for viscoelastic and hyperelastic models requires sophisticated experimental procedures and inverse analysis techniques. The parameter identification process is often ill-posed, with multiple parameter sets potentially yielding similar responses under specific loading conditions but diverging significantly under others.
Time-dependent behavior modeling remains particularly challenging for viscoelastic materials. Current FEA implementations struggle to efficiently handle the memory-dependent nature of viscoelasticity, especially for materials exhibiting complex relaxation spectra or those subjected to varying temperature conditions. The computational overhead of storing and processing historical deformation data creates significant memory management issues.
Mesh sensitivity represents another significant limitation, with solution accuracy heavily dependent on mesh refinement strategies. Hyperelastic materials, in particular, may exhibit localized deformations that require adaptive meshing techniques not fully matured in commercial FEA packages. This often forces engineers to employ overly refined meshes throughout the entire domain, further exacerbating computational inefficiency.
Interface modeling between different material types or between viscoelastic/hyperelastic materials and rigid bodies presents additional complications. Current contact algorithms often fail to accurately capture the complex interactions at these interfaces, particularly under dynamic loading conditions or when large sliding occurs.
Finally, there exists a significant gap between theoretical material models and their practical implementation in commercial FEA software. Many advanced constitutive models developed in academic research remain unavailable to industry practitioners, limiting the accuracy achievable in real-world engineering applications.
Numerical instability represents another major challenge, particularly when modeling materials undergoing large deformations. Convergence issues frequently arise during solution procedures, especially at strain rates approaching material limits or during complex loading-unloading cycles. These instabilities can lead to premature termination of simulations or, worse, physically unrealistic results that may go undetected.
Material parameter identification presents a persistent obstacle in practical implementations. The accurate determination of material constants for viscoelastic and hyperelastic models requires sophisticated experimental procedures and inverse analysis techniques. The parameter identification process is often ill-posed, with multiple parameter sets potentially yielding similar responses under specific loading conditions but diverging significantly under others.
Time-dependent behavior modeling remains particularly challenging for viscoelastic materials. Current FEA implementations struggle to efficiently handle the memory-dependent nature of viscoelasticity, especially for materials exhibiting complex relaxation spectra or those subjected to varying temperature conditions. The computational overhead of storing and processing historical deformation data creates significant memory management issues.
Mesh sensitivity represents another significant limitation, with solution accuracy heavily dependent on mesh refinement strategies. Hyperelastic materials, in particular, may exhibit localized deformations that require adaptive meshing techniques not fully matured in commercial FEA packages. This often forces engineers to employ overly refined meshes throughout the entire domain, further exacerbating computational inefficiency.
Interface modeling between different material types or between viscoelastic/hyperelastic materials and rigid bodies presents additional complications. Current contact algorithms often fail to accurately capture the complex interactions at these interfaces, particularly under dynamic loading conditions or when large sliding occurs.
Finally, there exists a significant gap between theoretical material models and their practical implementation in commercial FEA software. Many advanced constitutive models developed in academic research remain unavailable to industry practitioners, limiting the accuracy achievable in real-world engineering applications.
State-of-the-Art Implementation Approaches
01 Finite Element Implementation of Hyperelastic Material Models
Hyperelastic material models are implemented in finite element analysis to simulate materials that exhibit large deformations with nonlinear stress-strain relationships. These implementations typically involve the development of constitutive equations that capture the material's strain energy density function. The models account for material incompressibility, anisotropy, and strain-dependent behavior. Numerical algorithms are developed to solve the resulting nonlinear equations efficiently while ensuring stability and accuracy in the simulation results.- Finite Element Implementation of Viscoelastic Material Models: Viscoelastic material models are implemented in finite element analysis to simulate time-dependent behavior of materials that exhibit both viscous and elastic characteristics. These implementations typically involve mathematical formulations that capture stress relaxation, creep, and hysteresis phenomena. The finite element method discretizes the continuum into elements where viscoelastic constitutive equations are solved numerically, allowing for accurate prediction of material response under various loading conditions and time scales.
- Finite Element Implementation of Hyperelastic Material Models: Hyperelastic material models in finite element analysis are used to simulate materials that experience large deformations with nonlinear stress-strain relationships but return to their original shape upon unloading. These implementations typically involve strain energy density functions such as Neo-Hookean, Mooney-Rivlin, or Ogden models. The finite element formulation requires specialized algorithms to handle the nonlinear behavior and ensure numerical stability during large deformations, particularly important for modeling rubber-like materials and soft tissues.
- Combined Viscoelastic-Hyperelastic Models in FEA: Combined viscoelastic-hyperelastic models integrate both time-dependent and large deformation behaviors in a single finite element implementation. These hybrid models capture both the nonlinear elastic response at large strains and the time-dependent viscous effects. The implementation typically involves decomposing the deformation gradient into elastic and viscous components, with specialized numerical integration schemes to handle the different time scales. Such models are particularly valuable for simulating polymers, biological tissues, and advanced composite materials under complex loading conditions.
- Numerical Methods for Solving Nonlinear Material Models: Specialized numerical methods are essential for solving the complex equations arising from viscoelastic and hyperelastic material models in finite element analysis. These include implicit and explicit time integration schemes, Newton-Raphson iteration for nonlinear systems, and specialized solvers for the resulting algebraic equations. Advanced techniques such as adaptive time stepping, continuation methods, and stabilization algorithms are implemented to ensure convergence and accuracy, particularly when dealing with highly nonlinear material behavior or complex loading scenarios.
- Material Parameter Identification and Validation: Accurate implementation of viscoelastic and hyperelastic material models in finite element analysis requires robust methods for material parameter identification and validation. These implementations include optimization algorithms to fit experimental data to the material models, sensitivity analysis to determine the most influential parameters, and validation procedures to ensure the models accurately predict material behavior under conditions different from those used for calibration. Machine learning techniques are increasingly being used to enhance parameter identification efficiency and accuracy for complex material models.
02 Viscoelastic Material Modeling in FEA
Viscoelastic material models in finite element analysis capture time-dependent behaviors such as creep and stress relaxation. These implementations combine elastic and viscous components to represent materials that exhibit both solid-like and fluid-like characteristics. The models typically incorporate memory functions to account for loading history effects. Various numerical integration schemes are employed to handle the time-dependent constitutive equations, allowing for accurate simulation of materials under different loading rates and environmental conditions.Expand Specific Solutions03 Combined Viscoelastic-Hyperelastic Material Models
Combined viscoelastic-hyperelastic material models integrate both large deformation capabilities and time-dependent behavior in a single constitutive framework. These implementations typically separate the equilibrium (long-term) response from the non-equilibrium (transient) response. The models account for multiple relaxation mechanisms occurring at different time scales. Advanced numerical techniques are employed to handle the computational complexity arising from the combination of nonlinearity and time-dependency, enabling accurate simulation of complex materials like biological tissues and polymers.Expand Specific Solutions04 Numerical Methods for Material Model Implementation
Specialized numerical methods are developed for implementing viscoelastic and hyperelastic material models in finite element analysis. These include implicit and explicit time integration schemes, Newton-Raphson iteration techniques for nonlinear problems, and specialized element formulations. Adaptive meshing and multi-scale modeling approaches are employed to handle localized deformations and material heterogeneities. Stabilization techniques are implemented to overcome numerical challenges such as volumetric locking in nearly incompressible materials and convergence issues in highly nonlinear problems.Expand Specific Solutions05 Material Parameter Identification and Validation
Methods for identifying and validating material parameters for viscoelastic and hyperelastic models are implemented within finite element frameworks. These approaches include inverse methods that match simulation results with experimental data, optimization algorithms to minimize the difference between predicted and measured responses, and sensitivity analysis to determine the most influential parameters. Statistical techniques are employed to quantify uncertainty in material parameters. Validation procedures involve comparing simulation results against experimental data from multiple loading conditions to ensure model robustness.Expand Specific Solutions
Leading Software and Research Organizations
The finite element implementation of viscoelastic and hyperelastic material models market is currently in a growth phase, with increasing adoption across automotive, aerospace, and industrial sectors. The global market size is estimated to exceed $500 million, driven by demand for advanced simulation capabilities in product development. Leading players include established industrial giants like Sumitomo Rubber Industries, Boeing, and Siemens Industry Software, who leverage these technologies for product optimization. Academic institutions such as Peking University and University of California contribute significant research advancements. The technology shows varying maturity levels - with hyperelastic models being more established while viscoelastic implementations continue evolving, particularly in companies like TDK Corp, QUALCOMM, and Fujitsu that require precise material behavior prediction for electronics and components development.
Sumitomo Rubber Industries, Ltd.
Technical Solution: Sumitomo Rubber Industries has developed proprietary finite element implementation techniques for viscoelastic and hyperelastic material models specifically optimized for tire design and performance prediction. Their approach combines advanced constitutive modeling with experimental characterization to accurately capture the complex behavior of rubber compounds under various loading conditions. Their implementation incorporates multi-scale modeling techniques that bridge molecular dynamics simulations with continuum mechanics, allowing for more accurate prediction of material response. Sumitomo's technology employs specialized element formulations with enhanced hourglass control and mixed formulation techniques to address volumetric locking issues in nearly-incompressible materials. Their implementation includes temperature and frequency-dependent viscoelastic models using generalized Maxwell elements and Prony series representations, alongside sophisticated hyperelastic formulations that account for the Mullins effect and anisotropy introduced during manufacturing processes. The company has developed custom material subroutines (UMATs) that integrate with commercial FEA packages while maintaining proprietary algorithms.
Strengths: Highly specialized for rubber compound behavior prediction; excellent correlation with experimental data for tire applications; efficient numerical implementation allowing for complex full-tire simulations. Weaknesses: Solutions primarily optimized for tire industry applications; requires extensive material characterization testing; computationally intensive for full-scale product simulations.
The Boeing Co.
Technical Solution: Boeing has developed sophisticated finite element implementation techniques for viscoelastic and hyperelastic material models specifically tailored for aerospace applications. Their approach focuses on high-performance composite materials and elastomeric components subjected to extreme environmental conditions. Boeing's implementation incorporates advanced constitutive models that capture both the time-dependent viscoelastic behavior and large-strain hyperelastic response of materials used in aircraft structures and components. Their technology employs specialized element formulations with enhanced stability characteristics for handling the numerical challenges associated with nearly-incompressible materials. Boeing has developed proprietary material models that account for temperature dependence, frequency effects, and environmental aging, implemented through custom material subroutines (UMATs/VUMATs) that integrate with commercial FEA packages. Their implementation includes efficient numerical integration schemes for history-dependent viscoelastic behavior and robust parameter identification methodologies based on multi-objective optimization techniques. Boeing's approach also incorporates uncertainty quantification methods to account for material variability and manufacturing tolerances in their simulations.
Strengths: Highly specialized for aerospace applications; excellent prediction capabilities under extreme environmental conditions; robust validation against flight test data. Weaknesses: Solutions primarily optimized for aerospace industry applications; requires extensive material characterization across wide temperature and frequency ranges; limited public documentation due to proprietary nature.
Key Algorithms and Mathematical Frameworks
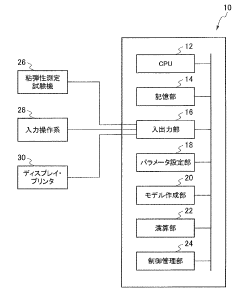
Viscoelastic material simulation method, structure simulation method, viscoelastic material simulation device, and program
PatentActiveJPWO2017077735A1
Innovation
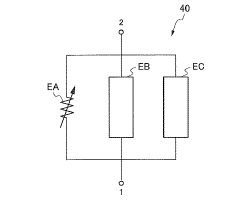
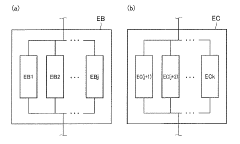
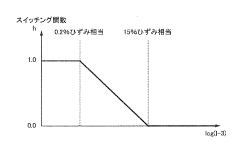
- A simulation method using a viscoelastic model with network elements that include a switching function to adjust viscoelastic parameters based on deformation magnitude, combining small and large deformation network elements to accurately represent viscoelastic characteristics.
Method of simulating viscoelastic material
PatentInactiveEP1526468A3
Innovation
- A method is proposed that divides the viscoelastic material and filler into finite elements to form separate models, including an interface model with distinct viscoelastic properties, to simulate deformation accurately by considering filler interactions and energy losses.
Computational Efficiency and Optimization Strategies
The implementation of finite element methods for viscoelastic and hyperelastic material models presents significant computational challenges due to the complex constitutive relationships and nonlinear behavior. Computational efficiency becomes a critical factor in practical applications, particularly for large-scale simulations or real-time analysis requirements.
Traditional implementation approaches often suffer from excessive computational costs, primarily due to the iterative nature of solving nonlinear equations and the need for frequent stiffness matrix updates. Recent advancements have focused on developing optimization strategies that maintain accuracy while reducing computational overhead.
Matrix-free methods have emerged as promising approaches for improving efficiency. These techniques avoid explicit formation and storage of the global stiffness matrix, instead computing matrix-vector products directly during the solution process. For hyperelastic models in particular, this can reduce memory requirements by 40-60% compared to conventional approaches.
Adaptive time-stepping algorithms provide another avenue for optimization. By dynamically adjusting the time step size based on solution behavior, these methods concentrate computational resources where they are most needed. Studies have shown that adaptive schemes can reduce overall computation time by 30-50% for viscoelastic simulations while maintaining solution accuracy within acceptable tolerances.
Parallelization strategies have become increasingly important as multi-core and distributed computing resources become more accessible. Domain decomposition methods that partition the problem across multiple processors have demonstrated near-linear scaling for up to hundreds of cores when properly implemented. GPU acceleration has shown particular promise, with speedups of 10-20x reported for specific hyperelastic material models.
Reduced-order modeling techniques offer substantial efficiency gains for certain applications. By projecting the high-dimensional finite element space onto a lower-dimensional subspace, these methods can dramatically reduce degrees of freedom while preserving essential behavior. For parametric studies involving viscoelastic materials, proper orthogonal decomposition approaches have demonstrated computational savings of up to 90%.
Implementation of consistent tangent operators remains crucial for achieving quadratic convergence in Newton-Raphson iterations. While computationally expensive to derive and implement, these operators significantly reduce the number of iterations required for convergence, particularly for highly nonlinear hyperelastic models.
Traditional implementation approaches often suffer from excessive computational costs, primarily due to the iterative nature of solving nonlinear equations and the need for frequent stiffness matrix updates. Recent advancements have focused on developing optimization strategies that maintain accuracy while reducing computational overhead.
Matrix-free methods have emerged as promising approaches for improving efficiency. These techniques avoid explicit formation and storage of the global stiffness matrix, instead computing matrix-vector products directly during the solution process. For hyperelastic models in particular, this can reduce memory requirements by 40-60% compared to conventional approaches.
Adaptive time-stepping algorithms provide another avenue for optimization. By dynamically adjusting the time step size based on solution behavior, these methods concentrate computational resources where they are most needed. Studies have shown that adaptive schemes can reduce overall computation time by 30-50% for viscoelastic simulations while maintaining solution accuracy within acceptable tolerances.
Parallelization strategies have become increasingly important as multi-core and distributed computing resources become more accessible. Domain decomposition methods that partition the problem across multiple processors have demonstrated near-linear scaling for up to hundreds of cores when properly implemented. GPU acceleration has shown particular promise, with speedups of 10-20x reported for specific hyperelastic material models.
Reduced-order modeling techniques offer substantial efficiency gains for certain applications. By projecting the high-dimensional finite element space onto a lower-dimensional subspace, these methods can dramatically reduce degrees of freedom while preserving essential behavior. For parametric studies involving viscoelastic materials, proper orthogonal decomposition approaches have demonstrated computational savings of up to 90%.
Implementation of consistent tangent operators remains crucial for achieving quadratic convergence in Newton-Raphson iterations. While computationally expensive to derive and implement, these operators significantly reduce the number of iterations required for convergence, particularly for highly nonlinear hyperelastic models.
Validation Methodologies and Experimental Correlation
Validation of finite element implementations for viscoelastic and hyperelastic material models requires rigorous methodologies to ensure computational results accurately reflect real-world material behavior. The primary validation approach involves comparing simulation outputs with analytical solutions for simple loading cases. For viscoelastic materials, relaxation tests and creep tests provide fundamental benchmarks where analytical solutions exist for specific material models such as Maxwell, Kelvin-Voigt, and Standard Linear Solid models. Similarly, hyperelastic models can be validated against analytical solutions for simple deformation modes including uniaxial tension, biaxial tension, and pure shear.
Beyond analytical comparisons, experimental correlation forms the cornerstone of comprehensive validation. This process typically begins with material characterization experiments designed to capture the specific behavior being modeled. For viscoelastic materials, dynamic mechanical analysis (DMA) measures storage and loss moduli across frequency ranges, while stress relaxation tests quantify time-dependent behavior. Hyperelastic materials require multi-axial testing protocols including uniaxial, biaxial, and volumetric compression tests to properly characterize their nonlinear response.
Mesh convergence studies represent another critical validation component, particularly for hyperelastic models where large deformations can lead to significant mesh distortion. These studies systematically refine element density until solution parameters stabilize, establishing the minimum mesh resolution required for accurate results. For viscoelastic materials, time-step sensitivity analysis serves a similar purpose, determining appropriate temporal discretization to capture rate-dependent phenomena.
Parameter identification methodologies constitute a crucial bridge between experimental data and computational models. Inverse methods utilizing optimization algorithms can systematically adjust model parameters to minimize differences between experimental measurements and simulation predictions. For complex material models with numerous parameters, sensitivity analysis helps identify which parameters most significantly influence model response, allowing focused optimization efforts.
Validation metrics must be carefully selected to quantify agreement between computational and experimental results. Common metrics include normalized root mean square error (NRMSE), correlation coefficients, and error in energy dissipation for viscoelastic materials. Visual comparison techniques such as hysteresis loop overlays provide intuitive assessment of model performance under cyclic loading conditions. Additionally, validation should extend beyond the calibration dataset to independent test cases, ensuring the model's predictive capability rather than merely its fitting ability.
Beyond analytical comparisons, experimental correlation forms the cornerstone of comprehensive validation. This process typically begins with material characterization experiments designed to capture the specific behavior being modeled. For viscoelastic materials, dynamic mechanical analysis (DMA) measures storage and loss moduli across frequency ranges, while stress relaxation tests quantify time-dependent behavior. Hyperelastic materials require multi-axial testing protocols including uniaxial, biaxial, and volumetric compression tests to properly characterize their nonlinear response.
Mesh convergence studies represent another critical validation component, particularly for hyperelastic models where large deformations can lead to significant mesh distortion. These studies systematically refine element density until solution parameters stabilize, establishing the minimum mesh resolution required for accurate results. For viscoelastic materials, time-step sensitivity analysis serves a similar purpose, determining appropriate temporal discretization to capture rate-dependent phenomena.
Parameter identification methodologies constitute a crucial bridge between experimental data and computational models. Inverse methods utilizing optimization algorithms can systematically adjust model parameters to minimize differences between experimental measurements and simulation predictions. For complex material models with numerous parameters, sensitivity analysis helps identify which parameters most significantly influence model response, allowing focused optimization efforts.
Validation metrics must be carefully selected to quantify agreement between computational and experimental results. Common metrics include normalized root mean square error (NRMSE), correlation coefficients, and error in energy dissipation for viscoelastic materials. Visual comparison techniques such as hysteresis loop overlays provide intuitive assessment of model performance under cyclic loading conditions. Additionally, validation should extend beyond the calibration dataset to independent test cases, ensuring the model's predictive capability rather than merely its fitting ability.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!