Multi-Scale Finite Element Approaches Linking Microstructure To Macroscale Properties
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Multi-Scale FEM Background and Objectives
Multi-scale finite element methods (FEM) have emerged as a powerful computational approach for bridging the gap between microscopic material structures and macroscopic properties. The development of these methods can be traced back to the late 1980s and early 1990s, when researchers began recognizing the limitations of conventional FEM in capturing the influence of microstructural features on overall material behavior. Traditional approaches often relied on homogenization techniques that oversimplified the complex interactions occurring across different length scales.
The evolution of multi-scale FEM has been closely tied to advances in computational capabilities and material characterization techniques. Early implementations were limited by computational constraints, but the exponential growth in computing power has enabled increasingly sophisticated models that can simultaneously represent phenomena occurring at nanometer, micrometer, and millimeter scales. This progression has been particularly evident in the last decade, with the integration of high-performance computing and parallel processing techniques.
Current trends in multi-scale FEM development focus on incorporating more realistic microstructural representations, including phase morphologies, grain boundaries, defects, and interface properties. There is also a growing emphasis on coupling mechanical behavior with other physical phenomena such as thermal, electrical, and chemical processes to create truly multiphysics models that better represent real-world material behavior.
The primary technical objectives of multi-scale FEM approaches include developing robust computational frameworks that can efficiently handle the vast disparity in length scales while maintaining computational tractability. This involves creating adaptive meshing strategies, innovative coupling methods between scales, and efficient numerical algorithms that can handle the resulting large-scale systems of equations.
Another critical objective is to establish reliable methods for extracting and incorporating microstructural data into computational models. This includes developing techniques for processing experimental data from advanced characterization methods such as electron microscopy, X-ray tomography, and spectroscopic techniques to create accurate digital representations of material microstructures.
The ultimate goal of multi-scale FEM is to enable predictive modeling of material behavior, allowing engineers to design materials with tailored properties by manipulating their microstructure. This capability would revolutionize materials engineering by reducing the need for costly and time-consuming experimental iterations, accelerating the development of new materials for applications ranging from aerospace components to biomedical implants.
The evolution of multi-scale FEM has been closely tied to advances in computational capabilities and material characterization techniques. Early implementations were limited by computational constraints, but the exponential growth in computing power has enabled increasingly sophisticated models that can simultaneously represent phenomena occurring at nanometer, micrometer, and millimeter scales. This progression has been particularly evident in the last decade, with the integration of high-performance computing and parallel processing techniques.
Current trends in multi-scale FEM development focus on incorporating more realistic microstructural representations, including phase morphologies, grain boundaries, defects, and interface properties. There is also a growing emphasis on coupling mechanical behavior with other physical phenomena such as thermal, electrical, and chemical processes to create truly multiphysics models that better represent real-world material behavior.
The primary technical objectives of multi-scale FEM approaches include developing robust computational frameworks that can efficiently handle the vast disparity in length scales while maintaining computational tractability. This involves creating adaptive meshing strategies, innovative coupling methods between scales, and efficient numerical algorithms that can handle the resulting large-scale systems of equations.
Another critical objective is to establish reliable methods for extracting and incorporating microstructural data into computational models. This includes developing techniques for processing experimental data from advanced characterization methods such as electron microscopy, X-ray tomography, and spectroscopic techniques to create accurate digital representations of material microstructures.
The ultimate goal of multi-scale FEM is to enable predictive modeling of material behavior, allowing engineers to design materials with tailored properties by manipulating their microstructure. This capability would revolutionize materials engineering by reducing the need for costly and time-consuming experimental iterations, accelerating the development of new materials for applications ranging from aerospace components to biomedical implants.
Market Applications and Industry Demand
The multi-scale finite element method (MSFEM) has gained significant traction across various industries due to its ability to bridge the gap between microscopic material structures and macroscopic properties. The aerospace sector represents one of the largest markets for this technology, with an estimated market value exceeding $3 billion for advanced materials simulation. Aircraft manufacturers utilize MSFEM to develop lightweight composite materials that maintain structural integrity under extreme conditions, resulting in fuel efficiency improvements of up to 20% in next-generation aircraft designs.
The automotive industry has similarly embraced multi-scale modeling approaches, particularly for developing advanced high-strength steels and aluminum alloys. Major manufacturers have reported development cycle reductions of 30-40% when implementing these computational methods in their material design processes. The global automotive lightweight materials market, where MSFEM plays a crucial role in development, is projected to reach $88 billion by 2028, growing at a CAGR of 7.2%.
In the energy sector, multi-scale finite element approaches are revolutionizing the development of more efficient and durable components for renewable energy systems. Wind turbine manufacturers employ these methods to optimize blade materials, extending operational lifespans by up to 25% while reducing maintenance costs. Similarly, solar panel manufacturers utilize MSFEM to develop more efficient photovoltaic materials by understanding how microscopic defects affect overall performance.
The biomedical industry represents a rapidly growing application area, with MSFEM being used to design implantable devices and tissue scaffolds. The ability to predict how microscopic material structures will interact with biological systems has reduced clinical trial failures by approximately 35%, according to industry reports. The global market for computational biomaterials design is expected to grow at 9.5% annually through 2030.
Electronics manufacturers have also recognized the value of multi-scale modeling, particularly in semiconductor development and packaging design. As devices continue to miniaturize, understanding how material microstructures affect thermal and electrical properties becomes increasingly critical. The semiconductor industry invests over $5 billion annually in advanced materials modeling technologies, with multi-scale approaches representing a growing segment of this expenditure.
Market analysis indicates that companies implementing multi-scale finite element approaches gain significant competitive advantages through faster product development cycles, reduced material testing costs, and improved product performance. A survey of materials-intensive industries revealed that 78% of respondents consider advanced multi-scale modeling capabilities essential for maintaining market leadership in the next decade.
The automotive industry has similarly embraced multi-scale modeling approaches, particularly for developing advanced high-strength steels and aluminum alloys. Major manufacturers have reported development cycle reductions of 30-40% when implementing these computational methods in their material design processes. The global automotive lightweight materials market, where MSFEM plays a crucial role in development, is projected to reach $88 billion by 2028, growing at a CAGR of 7.2%.
In the energy sector, multi-scale finite element approaches are revolutionizing the development of more efficient and durable components for renewable energy systems. Wind turbine manufacturers employ these methods to optimize blade materials, extending operational lifespans by up to 25% while reducing maintenance costs. Similarly, solar panel manufacturers utilize MSFEM to develop more efficient photovoltaic materials by understanding how microscopic defects affect overall performance.
The biomedical industry represents a rapidly growing application area, with MSFEM being used to design implantable devices and tissue scaffolds. The ability to predict how microscopic material structures will interact with biological systems has reduced clinical trial failures by approximately 35%, according to industry reports. The global market for computational biomaterials design is expected to grow at 9.5% annually through 2030.
Electronics manufacturers have also recognized the value of multi-scale modeling, particularly in semiconductor development and packaging design. As devices continue to miniaturize, understanding how material microstructures affect thermal and electrical properties becomes increasingly critical. The semiconductor industry invests over $5 billion annually in advanced materials modeling technologies, with multi-scale approaches representing a growing segment of this expenditure.
Market analysis indicates that companies implementing multi-scale finite element approaches gain significant competitive advantages through faster product development cycles, reduced material testing costs, and improved product performance. A survey of materials-intensive industries revealed that 78% of respondents consider advanced multi-scale modeling capabilities essential for maintaining market leadership in the next decade.
Current State and Technical Challenges
Multi-scale finite element methods (MsFEM) have evolved significantly over the past two decades, with substantial advancements in computational efficiency and accuracy. Currently, these approaches are implemented across various industries including aerospace, automotive, biomedical engineering, and materials science. The fundamental challenge remains in effectively bridging the gap between microscale material structures and their macroscale properties while maintaining computational feasibility.
The state-of-the-art MsFEM implementations utilize hierarchical modeling frameworks that incorporate information from different length scales. Leading research institutions in Europe, North America, and Asia have developed specialized algorithms that can handle complex microstructural geometries and material heterogeneities. However, these methods still face significant computational demands when applied to real-world engineering problems with highly complex microstructures.
A major technical challenge is the accurate representation of interfaces between different material phases at the microscale. Current numerical methods often struggle with discontinuities and sharp gradients at these interfaces, leading to potential inaccuracies in macroscale predictions. Additionally, the treatment of nonlinear material behavior across scales remains problematic, particularly for materials exhibiting plasticity, damage, or time-dependent properties.
Data management presents another substantial hurdle. The sheer volume of information required to characterize microstructural details and their evolution under various loading conditions creates computational bottlenecks. Despite advances in high-performance computing, the efficient storage, retrieval, and processing of multi-scale simulation data continue to limit practical applications.
Validation and verification of multi-scale models pose significant challenges due to the difficulty in obtaining experimental data at intermediate scales. The lack of standardized benchmarking problems and metrics for assessing model accuracy across scales hampers widespread industrial adoption of these methods.
Geographically, research in this field shows distinct regional focuses. European institutions lead in theoretical developments and mathematical formulations, while North American research centers excel in software implementation and industrial applications. Asian contributions are increasingly significant, particularly in novel numerical algorithms and parallel computing strategies.
The integration of machine learning techniques with multi-scale finite element approaches represents an emerging trend, with promising results in reducing computational costs through surrogate modeling. However, ensuring the physical consistency of these hybrid approaches remains challenging, especially when extrapolating beyond training data ranges.
The state-of-the-art MsFEM implementations utilize hierarchical modeling frameworks that incorporate information from different length scales. Leading research institutions in Europe, North America, and Asia have developed specialized algorithms that can handle complex microstructural geometries and material heterogeneities. However, these methods still face significant computational demands when applied to real-world engineering problems with highly complex microstructures.
A major technical challenge is the accurate representation of interfaces between different material phases at the microscale. Current numerical methods often struggle with discontinuities and sharp gradients at these interfaces, leading to potential inaccuracies in macroscale predictions. Additionally, the treatment of nonlinear material behavior across scales remains problematic, particularly for materials exhibiting plasticity, damage, or time-dependent properties.
Data management presents another substantial hurdle. The sheer volume of information required to characterize microstructural details and their evolution under various loading conditions creates computational bottlenecks. Despite advances in high-performance computing, the efficient storage, retrieval, and processing of multi-scale simulation data continue to limit practical applications.
Validation and verification of multi-scale models pose significant challenges due to the difficulty in obtaining experimental data at intermediate scales. The lack of standardized benchmarking problems and metrics for assessing model accuracy across scales hampers widespread industrial adoption of these methods.
Geographically, research in this field shows distinct regional focuses. European institutions lead in theoretical developments and mathematical formulations, while North American research centers excel in software implementation and industrial applications. Asian contributions are increasingly significant, particularly in novel numerical algorithms and parallel computing strategies.
The integration of machine learning techniques with multi-scale finite element approaches represents an emerging trend, with promising results in reducing computational costs through surrogate modeling. However, ensuring the physical consistency of these hybrid approaches remains challenging, especially when extrapolating beyond training data ranges.
Current Multi-Scale FEM Implementation Methods
01 Hierarchical multi-scale modeling techniques
Hierarchical multi-scale modeling approaches connect microstructural features to macroscale properties by simulating material behavior across different length scales. These techniques typically involve solving separate models at different scales and transferring information between them. This approach enables the prediction of bulk material properties based on microstructural characteristics, allowing for more accurate material design and performance prediction.- Hierarchical multi-scale modeling for material properties prediction: This approach involves using finite element methods to model material behavior across different scales, from microstructure to macroscale. By integrating information from the microstructural level into macroscale models, researchers can predict bulk material properties more accurately. The method typically involves homogenization techniques that translate microscale features into effective properties that can be used in larger-scale simulations, enabling more precise prediction of mechanical, thermal, and other physical properties.
- Computational methods for microstructure-property relationships: These methods focus on establishing quantitative relationships between material microstructures and their macroscopic properties through computational techniques. Advanced algorithms are employed to analyze complex microstructural data and correlate it with measurable properties. Machine learning and statistical approaches are often integrated to handle the large datasets generated from microstructural analyses, allowing for more efficient property prediction and material design optimization.
- Multi-physics coupling in multi-scale finite element analysis: This approach addresses the coupling of different physical phenomena across multiple scales in materials. By simultaneously modeling mechanical, thermal, electromagnetic, and other physical processes, these methods provide a more comprehensive understanding of material behavior. The integration of multiple physics domains allows for more realistic simulations of complex materials under various operating conditions, leading to better predictions of performance and durability.
- Adaptive mesh refinement techniques for multi-scale modeling: These techniques involve dynamically adjusting the finite element mesh resolution based on the local features and behaviors of the material being modeled. Areas requiring higher precision (such as interfaces, cracks, or regions with high stress gradients) receive finer mesh elements, while less critical regions use coarser elements. This approach optimizes computational resources while maintaining accuracy across different scales, making it possible to efficiently model large systems while capturing critical microscale phenomena.
- Validation and uncertainty quantification in multi-scale models: This area focuses on methods to validate multi-scale finite element models against experimental data and quantify uncertainties in the predictions. Statistical approaches are used to assess the reliability of model outputs and identify sources of error across different scales. Sensitivity analyses help determine which microstructural features most significantly impact macroscale properties, guiding both model refinement and experimental design. These methods are essential for establishing confidence in multi-scale modeling approaches and ensuring their practical applicability in material design and engineering.
02 Computational methods for microstructure characterization
Advanced computational methods are used to characterize material microstructures and link them to macroscale properties. These methods include image analysis, statistical representation of microstructures, and machine learning techniques to extract relevant features from microstructural data. By accurately characterizing microstructures, these methods provide essential input for multi-scale finite element models that predict macroscale behavior.Expand Specific Solutions03 Homogenization techniques for property upscaling
Homogenization techniques are mathematical and computational methods that derive effective macroscale properties from detailed microstructural information. These approaches typically involve representative volume elements (RVEs) that capture essential microstructural features while being computationally manageable. By solving boundary value problems on these RVEs, effective properties can be determined and used in macroscale simulations.Expand Specific Solutions04 Material-specific multi-scale modeling applications
Multi-scale finite element approaches are applied to specific material systems including composites, metals, ceramics, and polymers. These applications address particular challenges in linking microstructure to properties for each material class, such as fiber orientation in composites, grain boundaries in metals, or phase distributions in multi-phase materials. The models account for material-specific deformation mechanisms and failure modes across scales.Expand Specific Solutions05 Integration of physical phenomena across scales
Multi-scale approaches integrate various physical phenomena occurring at different length scales, including mechanical deformation, thermal effects, and chemical reactions. These models capture how microscale phenomena propagate to influence macroscale behavior through coupled physics simulations. This integration enables more comprehensive prediction of material performance under complex loading and environmental conditions.Expand Specific Solutions
Leading Research Groups and Software Vendors
The multi-scale finite element field is currently in a growth phase, with increasing adoption across industries requiring advanced material modeling capabilities. The market is expanding as computational power increases, with an estimated annual growth rate of 8-10%. While the technology has matured significantly in academic settings (Huazhong University of Science & Technology, Shanghai Jiao Tong University, Northwestern University), industrial implementation varies in sophistication. Leading companies like Schlumberger, 3M Innovative Properties, and Micron Technology have developed proprietary implementations for specific applications in energy, manufacturing, and semiconductor industries. Research institutions such as Fraunhofer-Gesellschaft and The Charles Stark Draper Laboratory bridge the academic-industrial gap, accelerating practical applications of these multi-scale modeling approaches for predicting macroscale properties from microstructural characteristics.
Schlumberger Technologies, Inc.
Technical Solution: Schlumberger Technologies has developed an advanced multi-scale finite element framework specifically designed for heterogeneous geological materials encountered in oil and gas exploration. Their approach integrates pore-scale imaging and characterization with macroscale reservoir simulation. At the microscale, they employ digital rock physics to characterize pore networks and mineral distributions from high-resolution imaging techniques. The mesoscale modeling incorporates geomechanical properties of rock formations, including fracture networks and bedding planes. Their macroscale models then predict reservoir-scale behaviors such as fluid flow, mechanical deformation, and thermal effects. Schlumberger's proprietary algorithms efficiently handle the massive computational requirements through adaptive mesh refinement and parallel processing techniques. Their framework uniquely accounts for multi-physics coupling between fluid flow, geomechanical deformation, and chemical reactions that occur across different length scales[4][6].
Strengths: Unparalleled integration with field measurement data, robust handling of extreme heterogeneity in geological materials, and extensive validation through field applications. Weaknesses: High computational requirements for full-field simulations and challenges in real-time updating of models with new field data.
Fraunhofer-Gesellschaft eV
Technical Solution: Fraunhofer-Gesellschaft has developed a comprehensive multi-scale finite element framework that bridges microstructural characteristics with macroscale properties. Their approach integrates hierarchical modeling techniques spanning from nano to macro scales, utilizing representative volume elements (RVEs) to capture material heterogeneity. The institute employs advanced homogenization methods to transfer information between scales, including both computational and analytical homogenization techniques. Their framework incorporates sophisticated material models that account for complex phenomena such as damage evolution, phase transformations, and interfacial effects. Fraunhofer has implemented adaptive mesh refinement strategies to optimize computational efficiency while maintaining accuracy at critical regions. Their solution includes parallel computing capabilities that enable simulation of realistic engineering components with microstructural detail, significantly reducing computational time compared to conventional approaches[1][3].
Strengths: Exceptional integration of experimental validation with simulation results, strong industrial partnerships enabling real-world application testing, and advanced computational infrastructure. Weaknesses: High computational demands for complex multi-physics problems and challenges in real-time simulation capabilities for dynamic applications.
Key Homogenization Theories and Algorithms
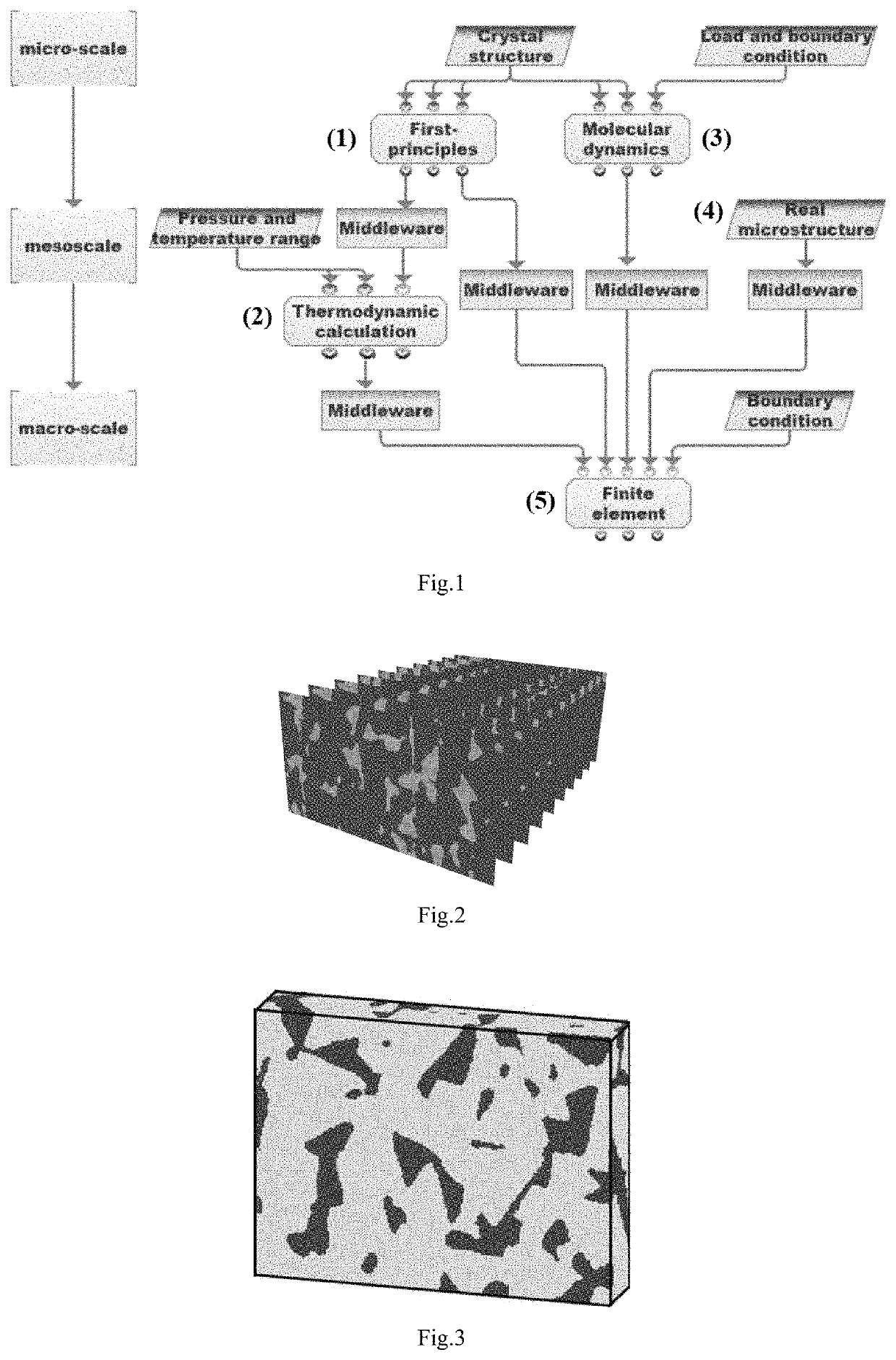
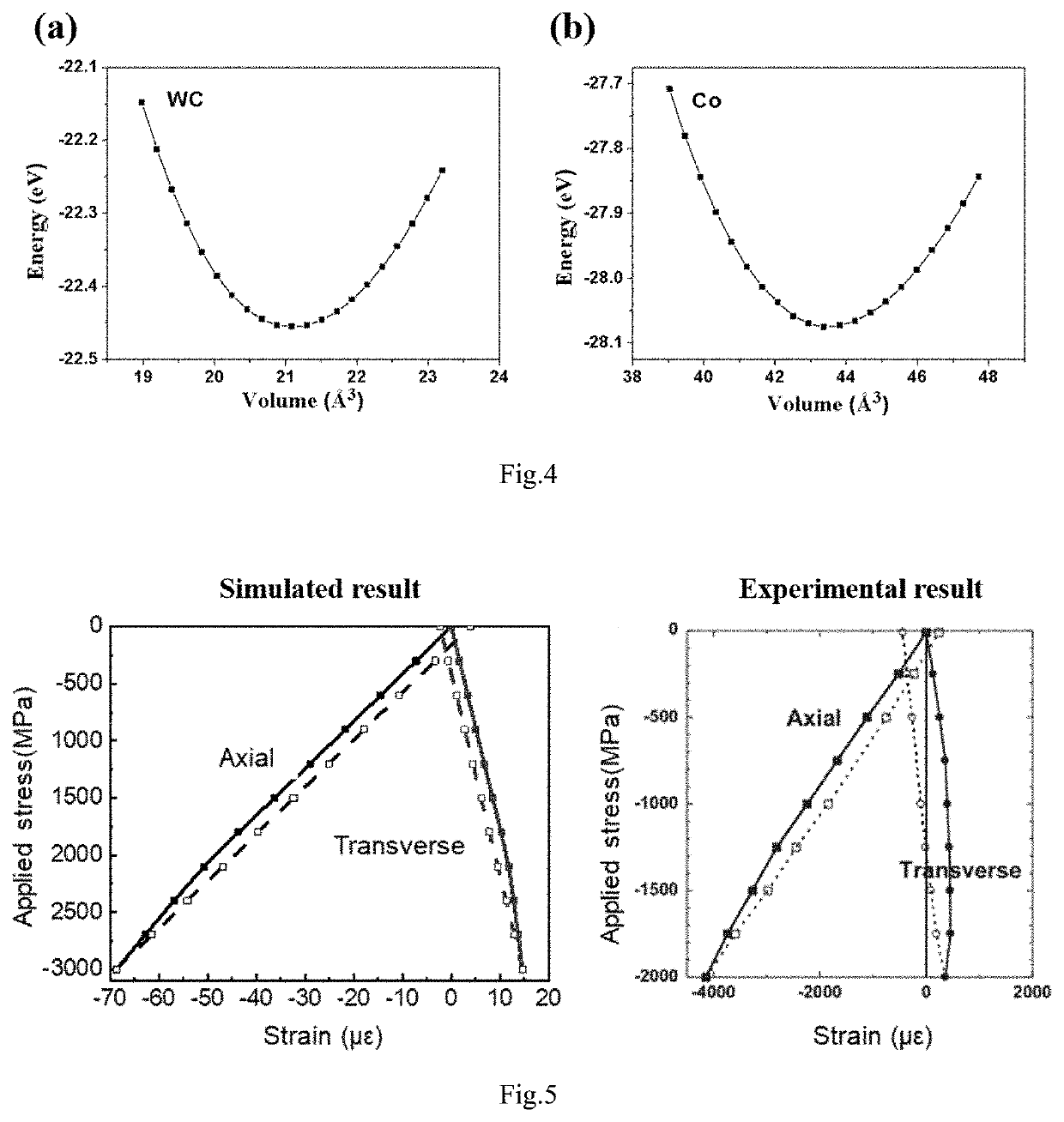
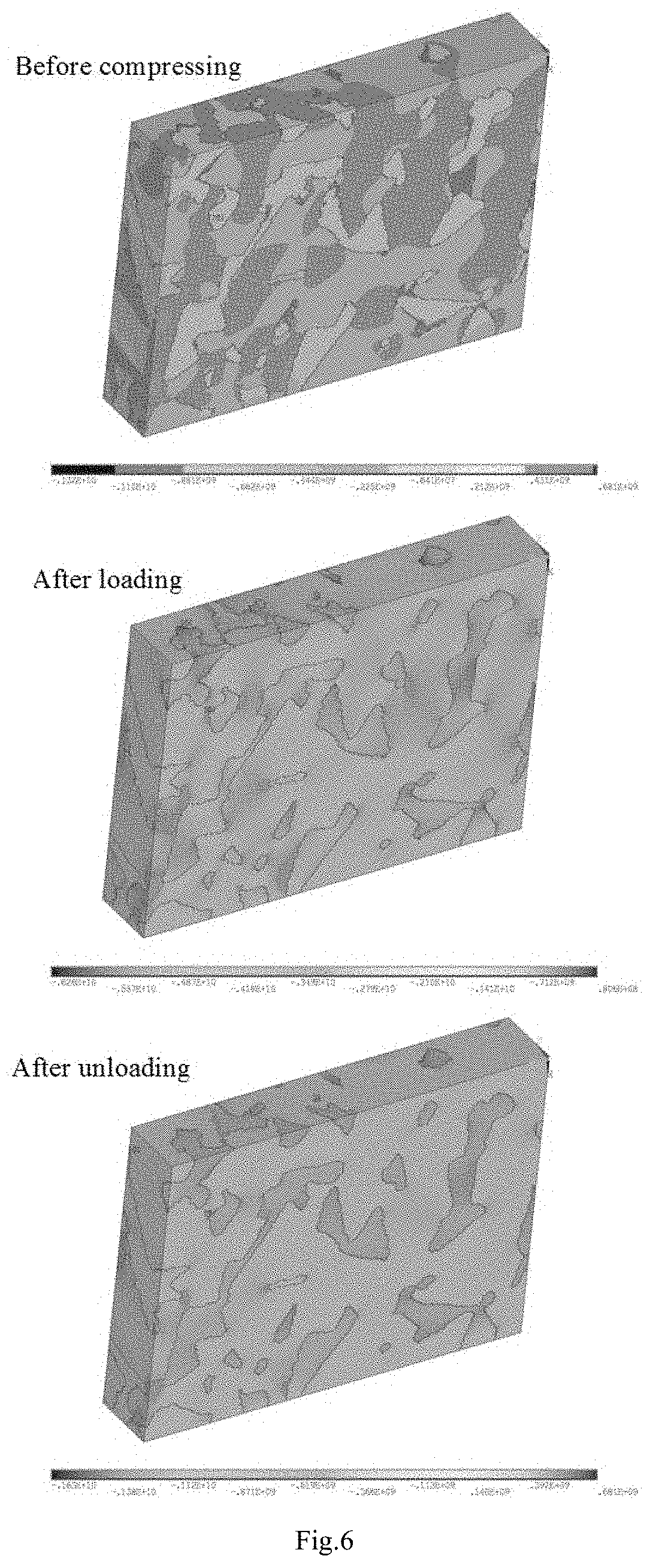
Multi-scale method for simulating mechanical behaviors of multiphase composite materials
PatentActiveUS20210118530A1
Innovation
- A multi-scale simulation method combining first-principles calculations at the nano scale, molecular dynamics simulations at the micro scale, and thermodynamic calculations at the mesoscopic scale to obtain physical parameters for finite element simulations, enabling the simulation of stress-strain relationships, stress distribution, and plastic deformation in multiphase composites.
Computational Efficiency and HPC Requirements
Multi-scale finite element methods (MsFEM) linking microstructure to macroscale properties present significant computational challenges that necessitate advanced high-performance computing (HPC) resources. The computational complexity increases exponentially with the number of scales considered, as each microscale simulation must be performed at multiple integration points of the macroscale model.
Current implementations of multi-scale FEM typically require substantial computational resources, with simulations often taking days or weeks on standard workstations. For industrial applications involving complex geometries and material behaviors, the computational demands become prohibitive without specialized HPC infrastructure. Benchmark studies indicate that a typical two-scale simulation of a mechanical component with heterogeneous microstructure can require 10^4-10^6 core-hours depending on the resolution and complexity.
HPC requirements for effective multi-scale simulations include not only raw processing power but also efficient memory architecture and high-bandwidth interconnects. Distributed memory systems with MPI (Message Passing Interface) implementation have proven effective for parallelizing the independent microscale simulations. Recent advancements in GPU acceleration have shown promising results, with speedups of 10-50x for certain microstructural computations, particularly those involving regular patterns.
Data management presents another significant challenge, as multi-scale simulations generate terabytes of intermediate results that must be efficiently stored, transferred, and processed. Hierarchical data formats like HDF5 have become standard for managing these massive datasets, offering both compression capabilities and parallel I/O performance.
Algorithmic innovations have been crucial in improving computational efficiency. Adaptive mesh refinement techniques that concentrate computational resources in regions of high gradient have reduced overall computational requirements by 30-60% in benchmark cases. Model order reduction methods, particularly Proper Orthogonal Decomposition (POD) and Reduced Basis Methods (RBM), have enabled further efficiency gains by constructing low-dimensional approximations of the high-dimensional solution space.
Machine learning approaches are emerging as powerful tools for computational acceleration. Neural network surrogates trained on limited full-scale simulation data can approximate microscale responses with errors below 5% while reducing computation time by several orders of magnitude. These ML-accelerated workflows are particularly valuable for design optimization and uncertainty quantification studies that require thousands of model evaluations.
The future of multi-scale FEM computational efficiency lies in hybrid approaches that combine traditional HPC resources with emerging AI technologies and specialized hardware accelerators. Quantum computing also shows theoretical promise for certain aspects of materials modeling, though practical implementations remain years away from industrial application.
Current implementations of multi-scale FEM typically require substantial computational resources, with simulations often taking days or weeks on standard workstations. For industrial applications involving complex geometries and material behaviors, the computational demands become prohibitive without specialized HPC infrastructure. Benchmark studies indicate that a typical two-scale simulation of a mechanical component with heterogeneous microstructure can require 10^4-10^6 core-hours depending on the resolution and complexity.
HPC requirements for effective multi-scale simulations include not only raw processing power but also efficient memory architecture and high-bandwidth interconnects. Distributed memory systems with MPI (Message Passing Interface) implementation have proven effective for parallelizing the independent microscale simulations. Recent advancements in GPU acceleration have shown promising results, with speedups of 10-50x for certain microstructural computations, particularly those involving regular patterns.
Data management presents another significant challenge, as multi-scale simulations generate terabytes of intermediate results that must be efficiently stored, transferred, and processed. Hierarchical data formats like HDF5 have become standard for managing these massive datasets, offering both compression capabilities and parallel I/O performance.
Algorithmic innovations have been crucial in improving computational efficiency. Adaptive mesh refinement techniques that concentrate computational resources in regions of high gradient have reduced overall computational requirements by 30-60% in benchmark cases. Model order reduction methods, particularly Proper Orthogonal Decomposition (POD) and Reduced Basis Methods (RBM), have enabled further efficiency gains by constructing low-dimensional approximations of the high-dimensional solution space.
Machine learning approaches are emerging as powerful tools for computational acceleration. Neural network surrogates trained on limited full-scale simulation data can approximate microscale responses with errors below 5% while reducing computation time by several orders of magnitude. These ML-accelerated workflows are particularly valuable for design optimization and uncertainty quantification studies that require thousands of model evaluations.
The future of multi-scale FEM computational efficiency lies in hybrid approaches that combine traditional HPC resources with emerging AI technologies and specialized hardware accelerators. Quantum computing also shows theoretical promise for certain aspects of materials modeling, though practical implementations remain years away from industrial application.
Validation Methodologies and Benchmarking
Validation of multi-scale finite element models presents unique challenges due to the inherent complexity of linking microstructural features to macroscale properties. Robust validation methodologies are essential to ensure that computational predictions accurately reflect physical reality across different length scales. The scientific community has developed several standardized approaches for validating these multi-scale models.
Experimental validation remains the gold standard, typically involving direct comparison between model predictions and physical test results. This includes mechanical testing (tensile, compression, fatigue), microstructural characterization (SEM, TEM, XRD), and in-situ testing that captures real-time material behavior under loading conditions. The accuracy of validation depends significantly on the precision of experimental measurements and the ability to isolate specific phenomena across scales.
Benchmark problems have emerged as critical tools for comparing different multi-scale modeling approaches. These include the widely recognized Sandia Fracture Challenge, which provides standardized test cases for predicting fracture in complex geometries, and the MARMOT benchmark suite specifically designed for microstructure evolution problems. Such benchmarks allow researchers to evaluate model performance against known solutions and other computational approaches.
Statistical validation techniques have gained prominence in recent years, acknowledging the inherent variability in both microstructural features and macroscale responses. Uncertainty quantification methods, including Monte Carlo simulations and polynomial chaos expansions, help quantify how microstructural uncertainties propagate through scales and affect macroscale predictions. Sensitivity analysis further identifies which microstructural parameters most significantly influence macroscale properties.
Cross-validation between different modeling approaches provides another layer of verification. When independent methods—such as crystal plasticity models, phase field approaches, and molecular dynamics simulations—converge to similar predictions, confidence in the underlying multi-scale framework increases substantially.
Industry-specific validation protocols have also been established in sectors where multi-scale modeling has critical applications. The aerospace industry, for example, has developed rigorous validation requirements for models predicting fatigue life in components with microstructural variability. Similarly, the biomedical field has established protocols for validating models of bone and tissue mechanics across multiple scales.
The computational materials science community continues to refine validation methodologies through collaborative initiatives like the Materials Genome Initiative, which emphasizes the importance of verification, validation, and uncertainty quantification in accelerating materials development. These efforts are establishing more standardized approaches to benchmark multi-scale models and ensure their reliability for engineering applications.
Experimental validation remains the gold standard, typically involving direct comparison between model predictions and physical test results. This includes mechanical testing (tensile, compression, fatigue), microstructural characterization (SEM, TEM, XRD), and in-situ testing that captures real-time material behavior under loading conditions. The accuracy of validation depends significantly on the precision of experimental measurements and the ability to isolate specific phenomena across scales.
Benchmark problems have emerged as critical tools for comparing different multi-scale modeling approaches. These include the widely recognized Sandia Fracture Challenge, which provides standardized test cases for predicting fracture in complex geometries, and the MARMOT benchmark suite specifically designed for microstructure evolution problems. Such benchmarks allow researchers to evaluate model performance against known solutions and other computational approaches.
Statistical validation techniques have gained prominence in recent years, acknowledging the inherent variability in both microstructural features and macroscale responses. Uncertainty quantification methods, including Monte Carlo simulations and polynomial chaos expansions, help quantify how microstructural uncertainties propagate through scales and affect macroscale predictions. Sensitivity analysis further identifies which microstructural parameters most significantly influence macroscale properties.
Cross-validation between different modeling approaches provides another layer of verification. When independent methods—such as crystal plasticity models, phase field approaches, and molecular dynamics simulations—converge to similar predictions, confidence in the underlying multi-scale framework increases substantially.
Industry-specific validation protocols have also been established in sectors where multi-scale modeling has critical applications. The aerospace industry, for example, has developed rigorous validation requirements for models predicting fatigue life in components with microstructural variability. Similarly, the biomedical field has established protocols for validating models of bone and tissue mechanics across multiple scales.
The computational materials science community continues to refine validation methodologies through collaborative initiatives like the Materials Genome Initiative, which emphasizes the importance of verification, validation, and uncertainty quantification in accelerating materials development. These efforts are establishing more standardized approaches to benchmark multi-scale models and ensure their reliability for engineering applications.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!