Finite Element Method: Fundamentals, Solver Choices And Modeling Practices
AUG 28, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
FEM Historical Development and Objectives
The Finite Element Method (FEM) emerged in the mid-20th century as a revolutionary approach to solving complex engineering problems. Its conceptual foundations can be traced back to the work of Richard Courant in the 1940s, who introduced the idea of piecewise polynomial solutions for variational problems. However, it was the aerospace industry in the 1950s that provided the catalyst for FEM's practical development, with engineers seeking more efficient methods to analyze aircraft structural integrity.
The 1960s marked a significant turning point with the publication of the first textbook on FEM by Zienkiewicz and Cheung, establishing a theoretical framework that would guide subsequent developments. During this period, FEM transitioned from a specialized tool used primarily in structural mechanics to a versatile methodology applicable across multiple engineering disciplines.
The evolution of computational capabilities in the 1970s and 1980s dramatically expanded FEM's practical applications. The introduction of commercial software packages like NASTRAN, ANSYS, and ABAQUS democratized access to finite element analysis, allowing engineers without specialized programming knowledge to leverage its capabilities. This period also saw the refinement of element formulations and the development of more sophisticated solution algorithms.
The primary objective of FEM has consistently been to provide numerical solutions for partial differential equations that govern physical phenomena where analytical solutions are impractical or impossible. By discretizing complex geometries into simpler elements, FEM transforms continuous problems into discrete approximations that can be solved computationally.
Modern FEM development aims to address several key objectives: improving computational efficiency to handle increasingly complex models; enhancing accuracy through adaptive meshing and higher-order elements; developing robust multiphysics capabilities to simulate coupled phenomena; and creating more intuitive user interfaces to reduce the expertise barrier for implementation.
The method's fundamental goal remains consistent: to provide engineers and scientists with a reliable tool for predicting the behavior of physical systems under various conditions, thereby reducing the need for costly physical prototyping and testing. As computational resources continue to advance, FEM's scope continues to expand into new domains including biomechanics, microelectronics, and fluid-structure interaction problems.
The trajectory of FEM development reflects a continuous refinement process driven by both theoretical advances and practical engineering needs, establishing it as one of the most important computational methods in modern engineering practice.
The 1960s marked a significant turning point with the publication of the first textbook on FEM by Zienkiewicz and Cheung, establishing a theoretical framework that would guide subsequent developments. During this period, FEM transitioned from a specialized tool used primarily in structural mechanics to a versatile methodology applicable across multiple engineering disciplines.
The evolution of computational capabilities in the 1970s and 1980s dramatically expanded FEM's practical applications. The introduction of commercial software packages like NASTRAN, ANSYS, and ABAQUS democratized access to finite element analysis, allowing engineers without specialized programming knowledge to leverage its capabilities. This period also saw the refinement of element formulations and the development of more sophisticated solution algorithms.
The primary objective of FEM has consistently been to provide numerical solutions for partial differential equations that govern physical phenomena where analytical solutions are impractical or impossible. By discretizing complex geometries into simpler elements, FEM transforms continuous problems into discrete approximations that can be solved computationally.
Modern FEM development aims to address several key objectives: improving computational efficiency to handle increasingly complex models; enhancing accuracy through adaptive meshing and higher-order elements; developing robust multiphysics capabilities to simulate coupled phenomena; and creating more intuitive user interfaces to reduce the expertise barrier for implementation.
The method's fundamental goal remains consistent: to provide engineers and scientists with a reliable tool for predicting the behavior of physical systems under various conditions, thereby reducing the need for costly physical prototyping and testing. As computational resources continue to advance, FEM's scope continues to expand into new domains including biomechanics, microelectronics, and fluid-structure interaction problems.
The trajectory of FEM development reflects a continuous refinement process driven by both theoretical advances and practical engineering needs, establishing it as one of the most important computational methods in modern engineering practice.
Industry Applications and Market Analysis
The Finite Element Method (FEM) has established itself as a cornerstone technology across numerous industries, with a global market valuation exceeding $6 billion in 2022 and projected to reach $9.5 billion by 2027, growing at a CAGR of approximately 9.6%. This growth is primarily driven by increasing demand for simulation-based engineering solutions that reduce physical prototyping costs and accelerate time-to-market.
In the automotive sector, FEM has become indispensable for structural analysis, crash testing, and noise-vibration-harshness (NVH) studies. Major manufacturers report development cost reductions of 20-30% through virtual prototyping using FEM, with companies like Toyota and Volkswagen investing heavily in advanced solver technologies to optimize vehicle designs before physical testing.
The aerospace industry represents another significant market segment, where FEM is critical for analyzing complex composite structures, thermal management systems, and aerodynamic performance. Boeing and Airbus have integrated FEM into their digital twin initiatives, creating comprehensive virtual models that mirror physical aircraft throughout their lifecycle.
Civil engineering applications continue to expand, with FEM being utilized for structural analysis of buildings, bridges, and infrastructure projects. The construction industry's adoption of Building Information Modeling (BIM) has created new opportunities for FEM integration, particularly in seismic analysis and sustainable design optimization.
The biomedical sector has emerged as a rapidly growing market for FEM applications, with a 15% annual growth rate in FEM software adoption. Applications include implant design, tissue engineering, and surgical planning. Patient-specific modeling using FEM has demonstrated potential to reduce surgical complications by up to 25% in certain procedures.
Energy sector applications span from wind turbine design optimization to nuclear containment analysis. Oil and gas companies utilize FEM for subsea equipment design and wellbore stability analysis, while renewable energy firms leverage it for optimizing solar panel structures and hydroelectric dam safety assessments.
Market analysis reveals a shift toward cloud-based FEM solutions, with subscription-based models gaining popularity among small and medium enterprises. This trend is democratizing access to high-performance computing resources previously available only to large corporations. The Asia-Pacific region, particularly China and India, represents the fastest-growing market for FEM technologies, driven by rapid industrialization and increasing R&D investments.
Competition among FEM software providers has intensified, with Ansys, Dassault Systèmes, and Siemens Digital Industries Software maintaining market leadership positions. Open-source alternatives like Code_Aster and FEniCS are gaining traction in academic and research environments, potentially disrupting traditional commercial software dominance in specialized application areas.
In the automotive sector, FEM has become indispensable for structural analysis, crash testing, and noise-vibration-harshness (NVH) studies. Major manufacturers report development cost reductions of 20-30% through virtual prototyping using FEM, with companies like Toyota and Volkswagen investing heavily in advanced solver technologies to optimize vehicle designs before physical testing.
The aerospace industry represents another significant market segment, where FEM is critical for analyzing complex composite structures, thermal management systems, and aerodynamic performance. Boeing and Airbus have integrated FEM into their digital twin initiatives, creating comprehensive virtual models that mirror physical aircraft throughout their lifecycle.
Civil engineering applications continue to expand, with FEM being utilized for structural analysis of buildings, bridges, and infrastructure projects. The construction industry's adoption of Building Information Modeling (BIM) has created new opportunities for FEM integration, particularly in seismic analysis and sustainable design optimization.
The biomedical sector has emerged as a rapidly growing market for FEM applications, with a 15% annual growth rate in FEM software adoption. Applications include implant design, tissue engineering, and surgical planning. Patient-specific modeling using FEM has demonstrated potential to reduce surgical complications by up to 25% in certain procedures.
Energy sector applications span from wind turbine design optimization to nuclear containment analysis. Oil and gas companies utilize FEM for subsea equipment design and wellbore stability analysis, while renewable energy firms leverage it for optimizing solar panel structures and hydroelectric dam safety assessments.
Market analysis reveals a shift toward cloud-based FEM solutions, with subscription-based models gaining popularity among small and medium enterprises. This trend is democratizing access to high-performance computing resources previously available only to large corporations. The Asia-Pacific region, particularly China and India, represents the fastest-growing market for FEM technologies, driven by rapid industrialization and increasing R&D investments.
Competition among FEM software providers has intensified, with Ansys, Dassault Systèmes, and Siemens Digital Industries Software maintaining market leadership positions. Open-source alternatives like Code_Aster and FEniCS are gaining traction in academic and research environments, potentially disrupting traditional commercial software dominance in specialized application areas.
Current FEM Capabilities and Limitations
The Finite Element Method (FEM) has evolved into a sophisticated computational tool with extensive capabilities across various engineering disciplines. Current implementations can handle complex multi-physics problems involving structural mechanics, fluid dynamics, heat transfer, electromagnetics, and their coupled interactions. Modern FEM software packages offer robust meshing capabilities that can accurately represent intricate geometries through adaptive and hierarchical meshing techniques, significantly improving solution accuracy while optimizing computational resources.
Commercial and open-source FEM solvers now incorporate advanced material models capable of simulating non-linear behaviors, including plasticity, viscoelasticity, hyperelasticity, and damage mechanics. These capabilities enable engineers to model complex material responses under various loading conditions with high fidelity. Additionally, time-dependent analyses have become increasingly sophisticated, allowing for accurate simulation of dynamic events, transient phenomena, and fatigue assessments.
Despite these advancements, FEM still faces significant limitations. Computational efficiency remains a persistent challenge, particularly for large-scale problems involving millions of degrees of freedom or highly non-linear phenomena. Even with high-performance computing resources, certain simulations may require prohibitively long solution times, limiting their practical application in time-sensitive design cycles.
Mesh dependency continues to be a critical issue, where solution accuracy is heavily influenced by mesh quality and refinement. This dependency can lead to inconsistent results across different mesh configurations, requiring extensive verification studies. Furthermore, singularities at geometric discontinuities often necessitate special treatment and can compromise solution accuracy in critical regions.
Contact modeling presents another significant challenge, particularly for problems involving large deformations, sliding interfaces, or complex frictional interactions. Current algorithms often struggle with convergence issues and may require extensive parameter tuning to achieve stable solutions. Similarly, multi-scale modeling remains difficult, as bridging microscopic and macroscopic phenomena efficiently within a unified FEM framework continues to be computationally intensive.
Uncertainty quantification and propagation represent emerging challenges in FEM applications. Traditional deterministic approaches fail to account for variabilities in material properties, loading conditions, and geometric tolerances, potentially leading to overly conservative or unreliable designs. While stochastic FEM methods are developing, they significantly increase computational demands and are not yet widely implemented in commercial software.
Commercial and open-source FEM solvers now incorporate advanced material models capable of simulating non-linear behaviors, including plasticity, viscoelasticity, hyperelasticity, and damage mechanics. These capabilities enable engineers to model complex material responses under various loading conditions with high fidelity. Additionally, time-dependent analyses have become increasingly sophisticated, allowing for accurate simulation of dynamic events, transient phenomena, and fatigue assessments.
Despite these advancements, FEM still faces significant limitations. Computational efficiency remains a persistent challenge, particularly for large-scale problems involving millions of degrees of freedom or highly non-linear phenomena. Even with high-performance computing resources, certain simulations may require prohibitively long solution times, limiting their practical application in time-sensitive design cycles.
Mesh dependency continues to be a critical issue, where solution accuracy is heavily influenced by mesh quality and refinement. This dependency can lead to inconsistent results across different mesh configurations, requiring extensive verification studies. Furthermore, singularities at geometric discontinuities often necessitate special treatment and can compromise solution accuracy in critical regions.
Contact modeling presents another significant challenge, particularly for problems involving large deformations, sliding interfaces, or complex frictional interactions. Current algorithms often struggle with convergence issues and may require extensive parameter tuning to achieve stable solutions. Similarly, multi-scale modeling remains difficult, as bridging microscopic and macroscopic phenomena efficiently within a unified FEM framework continues to be computationally intensive.
Uncertainty quantification and propagation represent emerging challenges in FEM applications. Traditional deterministic approaches fail to account for variabilities in material properties, loading conditions, and geometric tolerances, potentially leading to overly conservative or unreliable designs. While stochastic FEM methods are developing, they significantly increase computational demands and are not yet widely implemented in commercial software.
Contemporary Solver Technologies and Implementation
01 Finite Element Method for Structural Analysis
The finite element method is widely used for structural analysis in engineering applications. It involves dividing complex structures into smaller, simpler elements to analyze stress, strain, and deformation. This approach enables engineers to predict how structures will behave under various loading conditions and optimize designs for safety and performance. Advanced algorithms improve the accuracy and efficiency of these structural simulations.- Finite Element Method for Structural Analysis: Finite Element Method (FEM) is widely used for structural analysis in engineering applications. It involves dividing complex structures into smaller, simpler parts called finite elements and solving differential equations to predict structural behavior. This approach enables engineers to analyze stress distribution, deformation, and failure modes in various structures, improving design reliability and performance optimization.
- FEM in Electromagnetic Field Simulation: The Finite Element Method is applied to simulate electromagnetic fields and wave propagation. This technique allows for accurate modeling of complex electromagnetic phenomena by discretizing the computational domain into finite elements. Applications include antenna design, electromagnetic compatibility analysis, and electromagnetic wave propagation in various media, enabling more efficient design of electronic devices and communication systems.
- FEM Software Implementation and Optimization: Implementation of Finite Element Method in software requires specialized algorithms and optimization techniques to handle large-scale problems efficiently. This includes parallel computing approaches, mesh generation algorithms, and numerical solvers that reduce computational time while maintaining accuracy. Advanced software implementations enable the solution of increasingly complex engineering problems across multiple disciplines.
- FEM for Fluid Dynamics and Heat Transfer: Finite Element Method is employed to solve fluid dynamics and heat transfer problems by discretizing the governing equations over the computational domain. This approach enables accurate simulation of fluid flow patterns, temperature distributions, and heat transfer rates in complex geometries. Applications include HVAC system design, combustion analysis, and thermal management of electronic components.
- FEM in Manufacturing Process Simulation: The Finite Element Method is utilized to simulate manufacturing processes such as forming, casting, and machining. By modeling material behavior during these processes, engineers can predict defects, optimize process parameters, and improve product quality. This application of FEM helps reduce development time, minimize material waste, and enhance the efficiency of manufacturing operations.
02 Simulation and Modeling Applications
Finite element methods are employed in simulation and modeling across various fields including fluid dynamics, heat transfer, and electromagnetic analysis. These computational techniques allow for virtual testing of designs before physical prototyping, reducing development time and costs. The methods involve solving complex differential equations by approximating them with simpler algebraic equations over small domains, providing detailed insights into system behavior.Expand Specific Solutions03 Optimization of Finite Element Analysis
Optimization techniques enhance finite element analysis by improving computational efficiency and solution accuracy. These approaches include adaptive mesh refinement, parallel processing algorithms, and error estimation methods. By optimizing the finite element method, engineers can handle larger and more complex problems while reducing computational resources and time required for analysis, making it practical for real-time applications and large-scale industrial problems.Expand Specific Solutions04 Integration with CAD and Visualization Systems
Modern finite element method implementations integrate seamlessly with Computer-Aided Design (CAD) systems and advanced visualization tools. This integration allows engineers to move directly from design to analysis without cumbersome data conversion. Visualization capabilities enable intuitive interpretation of complex results through color-coded displays, animations, and interactive exploration of simulation data, helping engineers identify critical areas and make informed design decisions.Expand Specific Solutions05 Industry-Specific FEM Applications
Finite element methods have been adapted for specialized applications across various industries including automotive, aerospace, electronics, and medical device design. These industry-specific implementations incorporate domain knowledge and specialized material models to address unique challenges. For example, in electronics, FEM is used for thermal management and electromagnetic compatibility analysis, while in medical applications, it helps design implants and understand tissue mechanics.Expand Specific Solutions
Leading FEM Software Providers and Research Groups
The Finite Element Method (FEM) market is currently in a mature growth phase, characterized by established technologies and widespread adoption across industries. The global FEM software market size exceeds $6 billion, with steady annual growth of 7-9%. Leading the competitive landscape is ANSYS, Inc., which dominates with comprehensive simulation capabilities across multiple physics domains. Other significant players include Siemens Industry Software NV, Autodesk, and Dassault Systèmes, who offer integrated CAD-CAE solutions. The technology has reached high maturity in traditional applications like structural and thermal analysis, while emerging areas such as multi-physics coupling and cloud-based solvers represent growth frontiers. Academic institutions like Carnegie Mellon University and Nagoya University continue to advance theoretical foundations, while industry leaders like Boeing, Volkswagen AG, and Taiwan Semiconductor Manufacturing Co. drive practical applications and specialized implementations.
ANSYS, Inc.
Technical Solution: ANSYS has developed a comprehensive suite of finite element analysis (FEA) solvers that address various engineering challenges. Their technology implements both direct and iterative solvers with advanced algorithms for structural, thermal, fluid, electromagnetic, and multiphysics analyses. ANSYS employs adaptive mesh refinement techniques that automatically adjust element density in critical regions to improve solution accuracy while maintaining computational efficiency. Their parallel processing capabilities distribute computational workloads across multiple cores and clusters, significantly reducing solution times for large-scale problems. ANSYS's proprietary HPC (High-Performance Computing) framework enables efficient scaling from desktop workstations to enterprise-level computing resources, with documented performance improvements of up to 5-10x when utilizing their distributed solving architecture compared to traditional approaches.
Strengths: Industry-leading solver robustness handling highly nonlinear problems; seamless multiphysics coupling capabilities; extensive material model library; and superior convergence algorithms for complex contact problems. Weaknesses: Higher computational resource requirements compared to simplified solvers; steep learning curve for advanced features; and premium pricing structure that may be prohibitive for smaller organizations.
The Boeing Co.
Technical Solution: Boeing has developed proprietary FEA technology specifically optimized for aerospace applications, focusing on composite materials and large-scale structural analysis. Their approach implements specialized element formulations that accurately capture the behavior of composite laminates, including progressive failure mechanisms and delamination. Boeing's solvers incorporate advanced damage and fracture mechanics models that predict crack propagation and structural integrity under extreme loading conditions. Their technology features multi-scale modeling capabilities that bridge microscopic material behavior with macroscopic structural response, essential for accurate composite analysis. Boeing has pioneered efficient domain decomposition methods that enable analysis of complete aircraft structures with models containing tens of millions of degrees of freedom. Their solver architecture includes specialized contact algorithms that accurately model fastened and bonded joints, critical for aerospace structural integrity. Boeing's FEA implementation also features tight integration with their proprietary design and manufacturing systems, creating a seamless digital thread from concept to production.
Strengths: Unparalleled expertise in aerospace-specific applications; superior composite material modeling capabilities; and extensive validation against physical test data from decades of aircraft development. Weaknesses: Highly specialized for aerospace applications with limited applicability to other industries; proprietary nature limits broader adoption; and significant computational resources required for full-scale aircraft models.
Breakthrough Techniques in Element Formulation
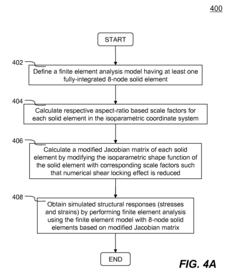
Fully-integrated hexahedral elements configured for reducing shear locking in finite element method
PatentActiveUS20110191072A1
Innovation
- Introducing aspect-ratio based scale factors to modify partial derivatives of the isoparametric shape function and directly modifying off-diagonal components in the local Jacobian matrix to alleviate spurious shear deformation modes, effectively reducing artificial transverse shear locking.
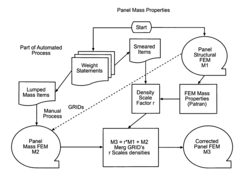
Finite element modeling method utilizing mass distribution
PatentInactiveUS7840386B2
Innovation
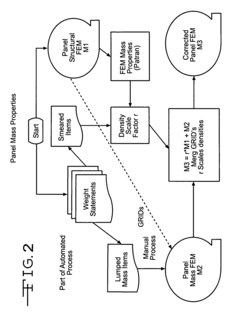
- The method involves partitioning an object into sub-objects, identifying structural and non-structural components, and constructing a finite element model using structural elements for the former and mass elements for the latter, with insignificant non-structural components incorporated by scaling the densities of structural elements, improving mass distribution accuracy.
Computational Performance Optimization Strategies
Computational performance optimization is a critical aspect of finite element method (FEM) implementation, directly impacting solution efficiency and feasibility for complex engineering problems. Modern FEM applications often involve millions of degrees of freedom, making performance optimization essential for practical industrial applications.
Matrix assembly optimization represents a fundamental strategy, as this process typically consumes 30-40% of computational resources in FEM workflows. Techniques such as element-by-element assembly and cache-aware algorithms can significantly reduce memory access patterns, yielding performance improvements of 2-3x in large-scale simulations. Additionally, sparse matrix storage formats like Compressed Sparse Row (CSR) and Compressed Sparse Column (CSC) minimize memory footprint while maintaining computational efficiency.
Solver acceleration techniques form another crucial optimization category. For linear systems, preconditioned iterative solvers such as Conjugate Gradient with Algebraic Multigrid preconditioning have demonstrated superior scaling properties compared to direct solvers when problem size exceeds approximately 100,000 degrees of freedom. GPU acceleration has revolutionized solver performance, with NVIDIA's cuSPARSE and cuSOLVER libraries delivering up to 10x speedup for appropriate problem classes.
Domain decomposition methods enable effective parallelization across distributed computing resources. Balanced partitioning algorithms minimize communication overhead while maximizing computational load balance. Modern implementations utilizing hybrid MPI/OpenMP paradigms can achieve near-linear scaling up to thousands of cores for well-structured problems.
Adaptive mesh refinement (AMR) strategies optimize computational resources by concentrating elements where solution gradients are steepest. Error estimators guide refinement decisions, ensuring solution accuracy while minimizing overall degrees of freedom. Studies indicate AMR can reduce computational requirements by 40-60% compared to uniform refinement approaches for problems with localized features.
Hardware-specific optimizations complete the performance enhancement toolkit. Vectorization through SIMD instructions (AVX-512, NEON) accelerates element-level calculations. Memory hierarchy optimization through blocking techniques improves cache utilization. Emerging heterogeneous computing approaches leverage specialized hardware like FPGAs for specific computational kernels, demonstrating promising results for time-critical applications requiring real-time FEM solutions.
Matrix assembly optimization represents a fundamental strategy, as this process typically consumes 30-40% of computational resources in FEM workflows. Techniques such as element-by-element assembly and cache-aware algorithms can significantly reduce memory access patterns, yielding performance improvements of 2-3x in large-scale simulations. Additionally, sparse matrix storage formats like Compressed Sparse Row (CSR) and Compressed Sparse Column (CSC) minimize memory footprint while maintaining computational efficiency.
Solver acceleration techniques form another crucial optimization category. For linear systems, preconditioned iterative solvers such as Conjugate Gradient with Algebraic Multigrid preconditioning have demonstrated superior scaling properties compared to direct solvers when problem size exceeds approximately 100,000 degrees of freedom. GPU acceleration has revolutionized solver performance, with NVIDIA's cuSPARSE and cuSOLVER libraries delivering up to 10x speedup for appropriate problem classes.
Domain decomposition methods enable effective parallelization across distributed computing resources. Balanced partitioning algorithms minimize communication overhead while maximizing computational load balance. Modern implementations utilizing hybrid MPI/OpenMP paradigms can achieve near-linear scaling up to thousands of cores for well-structured problems.
Adaptive mesh refinement (AMR) strategies optimize computational resources by concentrating elements where solution gradients are steepest. Error estimators guide refinement decisions, ensuring solution accuracy while minimizing overall degrees of freedom. Studies indicate AMR can reduce computational requirements by 40-60% compared to uniform refinement approaches for problems with localized features.
Hardware-specific optimizations complete the performance enhancement toolkit. Vectorization through SIMD instructions (AVX-512, NEON) accelerates element-level calculations. Memory hierarchy optimization through blocking techniques improves cache utilization. Emerging heterogeneous computing approaches leverage specialized hardware like FPGAs for specific computational kernels, demonstrating promising results for time-critical applications requiring real-time FEM solutions.
Verification and Validation Methodologies
Verification and validation (V&V) methodologies are critical components in ensuring the reliability and accuracy of Finite Element Method (FEM) simulations. These methodologies provide systematic approaches to assess whether the computational model accurately represents the physical phenomena it aims to simulate and whether the numerical implementation correctly solves the mathematical model.
The verification process focuses on the mathematical aspects of the simulation, confirming that the equations are solved correctly. This typically involves code verification through the method of manufactured solutions (MMS), where an analytical solution is artificially constructed, and the numerical solution is compared against it. Convergence studies are another essential verification technique, examining how solution errors decrease with mesh refinement according to theoretical rates. For complex problems, benchmark comparisons against established reference solutions provide confidence in the solver's accuracy.
Validation, conversely, addresses the physical realism of the simulation by comparing computational results with experimental data. This process requires careful experimental design with well-documented boundary conditions and material properties. Uncertainty quantification plays a vital role in validation, accounting for variabilities in both experimental measurements and simulation inputs. Statistical methods such as Monte Carlo simulations or polynomial chaos expansion help quantify how input uncertainties propagate through the model to affect outputs.
Mesh sensitivity analysis forms another crucial aspect of V&V methodologies, determining the appropriate element size and type for accurate results while maintaining computational efficiency. This involves systematic refinement of the mesh until solution parameters stabilize within acceptable tolerance levels. For time-dependent problems, temporal discretization studies similarly ensure that time-step sizes adequately capture the physics without introducing numerical artifacts.
Modern V&V approaches increasingly incorporate formal error estimation techniques, providing quantitative measures of simulation reliability. These include a posteriori error estimators that evaluate solution quality after computation and guide adaptive refinement strategies. Additionally, cross-validation techniques compare results from different modeling approaches or solver configurations to identify potential systematic errors.
Documentation standards for V&V have evolved significantly, with organizations like ASME and AIAA developing comprehensive guidelines. These standards emphasize transparent reporting of verification procedures, validation metrics, and uncertainty bounds, enabling reproducibility and facilitating peer review of simulation results. Adherence to these standards has become increasingly important as FEM simulations inform critical engineering decisions across industries.
The verification process focuses on the mathematical aspects of the simulation, confirming that the equations are solved correctly. This typically involves code verification through the method of manufactured solutions (MMS), where an analytical solution is artificially constructed, and the numerical solution is compared against it. Convergence studies are another essential verification technique, examining how solution errors decrease with mesh refinement according to theoretical rates. For complex problems, benchmark comparisons against established reference solutions provide confidence in the solver's accuracy.
Validation, conversely, addresses the physical realism of the simulation by comparing computational results with experimental data. This process requires careful experimental design with well-documented boundary conditions and material properties. Uncertainty quantification plays a vital role in validation, accounting for variabilities in both experimental measurements and simulation inputs. Statistical methods such as Monte Carlo simulations or polynomial chaos expansion help quantify how input uncertainties propagate through the model to affect outputs.
Mesh sensitivity analysis forms another crucial aspect of V&V methodologies, determining the appropriate element size and type for accurate results while maintaining computational efficiency. This involves systematic refinement of the mesh until solution parameters stabilize within acceptable tolerance levels. For time-dependent problems, temporal discretization studies similarly ensure that time-step sizes adequately capture the physics without introducing numerical artifacts.
Modern V&V approaches increasingly incorporate formal error estimation techniques, providing quantitative measures of simulation reliability. These include a posteriori error estimators that evaluate solution quality after computation and guide adaptive refinement strategies. Additionally, cross-validation techniques compare results from different modeling approaches or solver configurations to identify potential systematic errors.
Documentation standards for V&V have evolved significantly, with organizations like ASME and AIAA developing comprehensive guidelines. These standards emphasize transparent reporting of verification procedures, validation metrics, and uncertainty bounds, enabling reproducibility and facilitating peer review of simulation results. Adherence to these standards has become increasingly important as FEM simulations inform critical engineering decisions across industries.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!