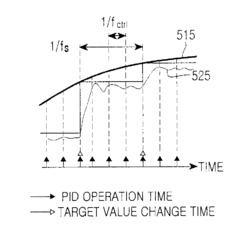
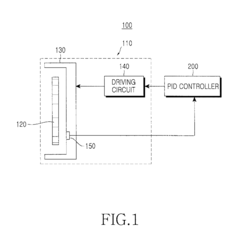
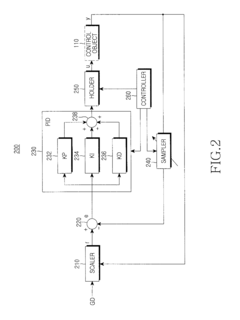
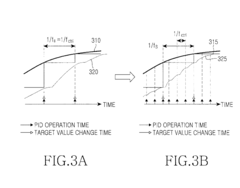
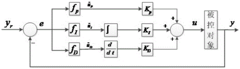
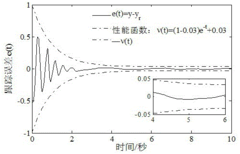
How Do PID Controllers Handle Nonlinear System Dynamics?

Proportional-Integral-Derivative (PID) control has evolved significantly since its inception in the early 20th century. Initially developed for ship steering systems by Nicholas Minorsky in 1922, PID controllers have become the most widely implemented control mechanism in industrial applications. Their evolution has been marked by transitions from mechanical and pneumatic implementations to electronic and digital versions, with each iteration bringing improvements in precision, reliability, and adaptability.

The fundamental principle of PID control has remained consistent throughout its evolution: combining proportional, integral, and derivative actions to minimize the error between a measured process variable and a desired setpoint. However, the methods for implementing these principles have undergone substantial refinement to address increasingly complex control challenges.

In the context of nonlinear system dynamics, PID controllers have faced significant evolutionary pressure. Traditional PID controllers were designed primarily for linear systems, operating under the assumption that system behavior remains consistent across operating ranges. This limitation became apparent as industrial processes grew more sophisticated, exhibiting nonlinear characteristics such as saturation, dead zones, and hysteresis that standard PID algorithms struggled to handle effectively.

The objectives of modern PID control in nonlinear systems have expanded beyond basic setpoint tracking to include robustness against disturbances, adaptation to changing system parameters, and optimization of performance metrics such as settling time and overshoot. These objectives have driven the development of advanced PID variants specifically designed to address nonlinear dynamics.

Gain scheduling emerged as an early approach to handling nonlinearity, where different PID parameters are applied depending on the operating region. This technique evolved into more sophisticated adaptive PID controllers that automatically adjust their parameters based on observed system behavior, effectively learning and adapting to nonlinearities in real-time.

Model-based PID tuning methods have also evolved to incorporate nonlinear system models, allowing for more accurate controller design that anticipates nonlinear responses. These approaches often utilize computational intelligence techniques such as fuzzy logic, neural networks, and genetic algorithms to optimize PID parameters across the full operating range of nonlinear systems.

The technological trajectory of PID control continues to advance toward greater integration with digital technologies. Modern objectives include developing self-tuning PID controllers that can automatically identify nonlinear system characteristics and adjust accordingly, as well as hybrid approaches that combine PID with other control strategies to leverage the simplicity of PID while addressing its limitations in handling complex nonlinear dynamics.

PID controllers have established a significant presence across various industrial sectors due to their ability to handle nonlinear system dynamics with relative simplicity and effectiveness. In the automotive industry, PID control systems manage nonlinear behaviors in engine control units, adaptive cruise control, and electronic stability programs. These applications require controllers that can adapt to varying road conditions, vehicle loads, and environmental factors that introduce nonlinearities into the system dynamics.

The process industry represents one of the largest markets for PID controllers in nonlinear applications, with an estimated global market value exceeding $2 billion. Chemical reactors, distillation columns, and batch processes all exhibit highly nonlinear characteristics due to complex reaction kinetics, thermodynamic relationships, and varying time constants. PID controllers, often enhanced with gain scheduling or adaptive tuning mechanisms, provide reliable control despite these challenges.

Robotics and motion control systems constitute another rapidly growing application area. Robotic arms, autonomous vehicles, and drones all operate under nonlinear dynamics influenced by inertia variations, friction, and aerodynamic effects. PID controllers, sometimes integrated with model predictive control or fuzzy logic systems, enable precise positioning and trajectory following in these complex mechanical systems.

The renewable energy sector has emerged as a significant market for advanced PID implementations. Wind turbines operate under highly nonlinear aerodynamic conditions that vary with wind speed, blade pitch angle, and rotational velocity. Similarly, solar tracking systems must compensate for nonlinear solar irradiance patterns. PID controllers with adaptive parameters help maximize energy capture under these varying conditions.

Healthcare applications represent a specialized but high-value market segment. Medical devices such as infusion pumps, ventilators, and anesthesia delivery systems must handle the nonlinear physiological responses of patients. PID controllers in these applications often incorporate safety constraints and patient-specific parameter adjustments to ensure reliable performance despite biological variability.

The HVAC industry widely employs PID controllers to manage nonlinear thermal dynamics in buildings. Temperature control systems must account for nonlinearities arising from varying occupancy, external weather conditions, and the thermodynamic properties of different building materials. Advanced PID implementations with weather prediction integration and occupancy sensing optimize energy efficiency while maintaining comfort.

Aerospace applications demand particularly robust PID implementations for flight control systems. Aircraft dynamics are inherently nonlinear, varying significantly with altitude, speed, and loading conditions. PID controllers, often augmented with gain scheduling based on flight envelope parameters, provide stable control across diverse operating conditions.

Nonlinear systems present significant challenges for PID controllers, which were originally designed for linear system dynamics. The fundamental issue lies in the inherent mismatch between the linear control methodology of PID and the complex behaviors exhibited by nonlinear systems. In nonlinear systems, the relationship between input and output varies depending on the operating point, making it difficult for a fixed-gain PID controller to maintain consistent performance across the entire operating range.

One of the primary challenges is gain scheduling, as the optimal PID parameters for one operating region may be entirely unsuitable for another. This necessitates adaptive tuning mechanisms or gain scheduling approaches that can adjust controller parameters based on the current system state. Without such adaptations, nonlinear systems controlled by standard PID controllers often exhibit oscillatory behavior, overshoot, or even instability when operating conditions change.

System time delays and dead zones, which are common in many industrial processes, further complicate PID control of nonlinear systems. These phenomena can cause traditional PID controllers to overcompensate, leading to control instability. Additionally, many nonlinear systems exhibit hysteresis effects, where the system response depends not only on the current input but also on the history of inputs, creating memory effects that standard PID controllers cannot inherently account for.

Saturation effects represent another significant challenge. When actuators reach their physical limits, the control system enters a nonlinear regime that can lead to integral windup in PID controllers. This occurs when the integral term continues to accumulate error even though the actuator cannot provide additional output, resulting in delayed response and potential instability when the system returns to normal operating conditions.

Model uncertainty compounds these challenges, as real-world nonlinear systems rarely conform perfectly to theoretical models. Environmental factors, component aging, and unpredictable disturbances introduce additional nonlinearities that are difficult to characterize and compensate for using standard PID approaches. This uncertainty often necessitates robust control strategies that can maintain stability despite model inaccuracies.

The coupling between multiple variables in multivariable nonlinear systems presents yet another layer of complexity. Traditional SISO (Single-Input-Single-Output) PID controllers struggle with these interactions, as changes in one control loop can significantly affect others, leading to complex dynamic behaviors that simple PID structures cannot adequately manage without sophisticated decoupling mechanisms.

These challenges have driven research into enhanced PID architectures and hybrid approaches that combine PID with other control methodologies to better handle nonlinear dynamics while maintaining the simplicity and reliability that have made PID controllers the industry standard for decades.

The PID controller market for nonlinear systems is in a mature growth phase, with an estimated global market size exceeding $2 billion and expanding at 5-7% annually. While PID technology is well-established, innovations in handling nonlinear dynamics continue to emerge. Leading industrial players like Yamaha Motor, Samsung Electronics, and Honda Motor focus on practical implementations across automotive and robotics applications. Delta Electronics and Infineon Technologies Austria are advancing adaptive PID solutions for power systems. Academic institutions, particularly Zhejiang University, Southeast University, and Shandong University, are pioneering research in intelligent PID variants with gain scheduling and fuzzy logic approaches. The integration of machine learning with traditional PID control represents the cutting edge, with companies like AVL List developing hybrid solutions for complex nonlinear industrial processes.

The stability analysis of PID controllers in nonlinear systems represents a critical area of investigation due to the inherent complexity and unpredictability of nonlinear dynamics. Traditional linear stability analysis methods, such as Routh-Hurwitz criteria or root locus techniques, become insufficient when applied to nonlinear systems controlled by PID mechanisms.

Lyapunov stability theory provides a fundamental framework for analyzing nonlinear PID control systems. By constructing appropriate Lyapunov functions, engineers can establish stability regions where PID controllers maintain system equilibrium despite nonlinearities. These analyses often reveal that stability is highly dependent on the controller gains (Kp, Ki, Kd) in relation to the specific nonlinear characteristics of the plant.

Describing function analysis offers another valuable approach for stability assessment, particularly when dealing with nonlinear elements like saturation, dead zones, or hysteresis. This technique approximates nonlinear elements with frequency-dependent gains, enabling prediction of limit cycles and stability boundaries for PID-controlled nonlinear systems.

Phase plane analysis provides geometric insights into nonlinear system behavior under PID control. By plotting system trajectories in state space, engineers can identify stable and unstable regions, as well as the influence of PID parameters on the system's dynamic response. This visual representation helps in understanding how nonlinearities affect closed-loop stability.

Input-to-State Stability (ISS) concepts extend traditional stability notions to account for bounded disturbances in nonlinear PID applications. ISS analysis ensures that system states remain bounded when inputs are bounded, a crucial consideration for practical nonlinear control implementations.

Region of attraction (ROA) determination represents another essential aspect of nonlinear PID stability analysis. The ROA defines the set of initial conditions from which the system converges to the desired equilibrium point. PID tuning significantly impacts the size and shape of this region, with implications for system robustness.

Computational methods, including numerical continuation techniques and sum-of-squares programming, have emerged as powerful tools for quantitative stability analysis of nonlinear PID systems. These approaches enable precise characterization of stability boundaries and performance limitations that would be difficult to determine analytically.

Recent advances in robust control theory have led to stability guarantees for certain classes of nonlinear systems under PID control, particularly when combined with adaptive or gain-scheduling techniques that adjust controller parameters based on operating conditions.

Evaluating PID controller performance in nonlinear systems requires specialized metrics that go beyond traditional linear system benchmarks. The Integral Absolute Error (IAE), Integral Square Error (ISE), and Integral Time-weighted Absolute Error (ITAE) serve as fundamental quantitative measures for assessing control performance. IAE provides a straightforward assessment of error magnitude over time, while ISE penalizes larger errors more heavily. ITAE is particularly valuable for nonlinear systems as it emphasizes persistent errors, which often occur when PID controllers struggle with nonlinearities.

Rise time, settling time, and overshoot percentage remain important metrics but must be interpreted differently in nonlinear contexts. For instance, a nonlinear system may exhibit variable rise times depending on operating regions, requiring region-specific benchmarking rather than single-value targets. Similarly, overshoot characteristics may vary dramatically across the operating range of a nonlinear system.

Robustness metrics become especially critical when evaluating PID controllers in nonlinear environments. Gain and phase margins must be assessed across multiple operating points to ensure stability throughout the system's operating range. The sensitivity function, which measures disturbance rejection capability, should be evaluated at various operating points to create a comprehensive performance profile.

Industry-specific benchmarking standards have emerged to address the challenges of nonlinear control evaluation. The IEEE 1512 standard provides guidelines for testing industrial controllers in nonlinear applications, while the ISA-75.25.01 standard focuses specifically on control valve performance in nonlinear flow conditions. These standards typically specify test procedures that exercise the controller across its entire operating range rather than at isolated points.

Simulation-based benchmarking has become increasingly important, with standardized nonlinear test cases such as the Van der Pol oscillator, inverted pendulum, and chemical reactor models serving as common reference problems. Performance on these benchmark problems allows for meaningful comparison between different PID tuning methods and controller architectures designed for nonlinear systems.

Real-time performance metrics, including computational efficiency and implementation overhead, must also be considered when deploying PID controllers in nonlinear applications. This is particularly relevant for embedded systems where processing resources may be limited, yet the controller must respond quickly to changing system dynamics.

The development of standardized performance indices that combine multiple metrics into composite scores has gained traction in recent years, offering a more holistic view of controller performance across the nonlinear operating range. These indices typically weight different performance aspects according to application-specific requirements, providing a more nuanced evaluation framework than traditional single-metric approaches.