Robust PID Controller Design For Systems With Uncertainty
SEP 5, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
PID Control Evolution and Design Objectives
Proportional-Integral-Derivative (PID) control has evolved significantly since its inception in the early 20th century. Initially developed for ship steering systems by Nicholas Minorsky in 1922, PID controllers have become the most widely implemented control algorithm in industrial applications due to their simplicity, reliability, and effectiveness. The evolution of PID control has been marked by continuous refinement in both theoretical understanding and practical implementation methodologies.
During the 1940s and 1950s, the mathematical foundations of PID control were established, with researchers developing transfer function representations and stability analysis techniques. The 1960s saw the transition from pneumatic to electronic implementations, significantly enhancing control precision and response times. By the 1970s and 1980s, microprocessor-based digital PID controllers emerged, offering unprecedented flexibility in parameter tuning and implementation.
The contemporary landscape of PID control is characterized by advanced adaptive and auto-tuning capabilities, which automatically adjust controller parameters in response to changing system dynamics. This evolution reflects the persistent need for robust control solutions that can maintain performance despite uncertainties in system behavior.
The primary objective of robust PID controller design is to develop control systems that maintain stability and performance specifications despite variations in plant parameters, external disturbances, and modeling inaccuracies. This objective addresses the fundamental challenge in control engineering: bridging the gap between theoretical models and real-world systems that invariably contain uncertainties.
Specific design objectives include disturbance rejection, where the controller must minimize the impact of external disturbances on system output; reference tracking, ensuring the system follows desired setpoints with minimal error; and robustness to parameter variations, maintaining performance despite changes in system characteristics over time or operating conditions.
For systems with uncertainty, these objectives become particularly challenging. Uncertainties may manifest as parametric variations, unmodeled dynamics, or external disturbances with unknown characteristics. The robust PID design must therefore establish stability margins that accommodate these uncertainties while still achieving desired performance metrics such as settling time, overshoot, and steady-state error.
Recent technological trends have pushed PID control evolution toward integration with advanced techniques such as fuzzy logic, neural networks, and model predictive control, creating hybrid approaches that leverage the simplicity of PID while addressing its limitations in handling complex nonlinear systems with significant uncertainties.
During the 1940s and 1950s, the mathematical foundations of PID control were established, with researchers developing transfer function representations and stability analysis techniques. The 1960s saw the transition from pneumatic to electronic implementations, significantly enhancing control precision and response times. By the 1970s and 1980s, microprocessor-based digital PID controllers emerged, offering unprecedented flexibility in parameter tuning and implementation.
The contemporary landscape of PID control is characterized by advanced adaptive and auto-tuning capabilities, which automatically adjust controller parameters in response to changing system dynamics. This evolution reflects the persistent need for robust control solutions that can maintain performance despite uncertainties in system behavior.
The primary objective of robust PID controller design is to develop control systems that maintain stability and performance specifications despite variations in plant parameters, external disturbances, and modeling inaccuracies. This objective addresses the fundamental challenge in control engineering: bridging the gap between theoretical models and real-world systems that invariably contain uncertainties.
Specific design objectives include disturbance rejection, where the controller must minimize the impact of external disturbances on system output; reference tracking, ensuring the system follows desired setpoints with minimal error; and robustness to parameter variations, maintaining performance despite changes in system characteristics over time or operating conditions.
For systems with uncertainty, these objectives become particularly challenging. Uncertainties may manifest as parametric variations, unmodeled dynamics, or external disturbances with unknown characteristics. The robust PID design must therefore establish stability margins that accommodate these uncertainties while still achieving desired performance metrics such as settling time, overshoot, and steady-state error.
Recent technological trends have pushed PID control evolution toward integration with advanced techniques such as fuzzy logic, neural networks, and model predictive control, creating hybrid approaches that leverage the simplicity of PID while addressing its limitations in handling complex nonlinear systems with significant uncertainties.
Industrial Demand Analysis for Robust Control Systems
The industrial demand for robust control systems has witnessed significant growth across various sectors, particularly in manufacturing, process industries, and automation. This surge is primarily driven by the increasing complexity of industrial processes and the need for maintaining optimal performance despite uncertainties and disturbances. Robust PID controllers, specifically designed to handle system uncertainties, have become essential components in modern industrial control systems.
Manufacturing industries, including automotive, aerospace, and electronics, represent the largest market segment for robust control systems. These industries require precise control of complex machinery and processes where variations in operating conditions can significantly impact product quality. According to recent market analyses, manufacturing sectors account for approximately 40% of the total robust control systems market, with an annual growth rate exceeding the industry average.
Process industries, including chemical, petrochemical, and pharmaceutical sectors, form another significant market segment. These industries deal with inherently uncertain processes where parameters can vary due to raw material inconsistencies, equipment aging, or environmental factors. The demand for robust PID controllers in these sectors stems from the critical need to maintain product quality and process safety despite these uncertainties.
Energy production and distribution systems represent an emerging market with substantial growth potential. As renewable energy sources become more prevalent, the need for robust control systems capable of handling the inherent variability of these resources has increased dramatically. Wind turbines, solar panels, and grid management systems all require controllers that can maintain stability despite fluctuating inputs and changing environmental conditions.
The healthcare and biomedical industries have also shown increasing interest in robust control systems, particularly for medical devices and automated treatment systems. These applications demand controllers that can adapt to patient-specific variations while maintaining safety and efficacy.
From a geographical perspective, developed regions like North America and Europe currently dominate the market for robust control systems, accounting for over 60% of global demand. However, the Asia-Pacific region, led by China and India, is experiencing the fastest growth rate due to rapid industrialization and increasing automation in manufacturing processes.
The market is further driven by stringent regulatory requirements across industries that mandate precise control and monitoring of processes. Additionally, the growing trend toward Industry 4.0 and smart manufacturing has amplified the need for advanced control systems that can integrate with digital platforms while maintaining robustness against uncertainties.
Manufacturing industries, including automotive, aerospace, and electronics, represent the largest market segment for robust control systems. These industries require precise control of complex machinery and processes where variations in operating conditions can significantly impact product quality. According to recent market analyses, manufacturing sectors account for approximately 40% of the total robust control systems market, with an annual growth rate exceeding the industry average.
Process industries, including chemical, petrochemical, and pharmaceutical sectors, form another significant market segment. These industries deal with inherently uncertain processes where parameters can vary due to raw material inconsistencies, equipment aging, or environmental factors. The demand for robust PID controllers in these sectors stems from the critical need to maintain product quality and process safety despite these uncertainties.
Energy production and distribution systems represent an emerging market with substantial growth potential. As renewable energy sources become more prevalent, the need for robust control systems capable of handling the inherent variability of these resources has increased dramatically. Wind turbines, solar panels, and grid management systems all require controllers that can maintain stability despite fluctuating inputs and changing environmental conditions.
The healthcare and biomedical industries have also shown increasing interest in robust control systems, particularly for medical devices and automated treatment systems. These applications demand controllers that can adapt to patient-specific variations while maintaining safety and efficacy.
From a geographical perspective, developed regions like North America and Europe currently dominate the market for robust control systems, accounting for over 60% of global demand. However, the Asia-Pacific region, led by China and India, is experiencing the fastest growth rate due to rapid industrialization and increasing automation in manufacturing processes.
The market is further driven by stringent regulatory requirements across industries that mandate precise control and monitoring of processes. Additionally, the growing trend toward Industry 4.0 and smart manufacturing has amplified the need for advanced control systems that can integrate with digital platforms while maintaining robustness against uncertainties.
Current Challenges in PID Control Under Uncertainty
Despite significant advancements in control theory, PID controllers operating in uncertain environments continue to face substantial challenges. The fundamental issue stems from the inherent trade-off between robustness and performance. As systems become more complex and operate in increasingly variable conditions, traditional PID tuning methods often prove inadequate when confronted with parametric uncertainties, unmodeled dynamics, and external disturbances.
Parameter uncertainty presents a particularly vexing challenge, as real-world systems rarely match their mathematical models perfectly. Manufacturing variations, component aging, and environmental factors can cause system parameters to deviate significantly from nominal values. Conventional PID controllers, tuned for specific operating conditions, frequently exhibit degraded performance or even instability when these parameters drift beyond anticipated ranges.
Disturbance rejection capabilities of standard PID implementations are often insufficient for systems operating in harsh or unpredictable environments. External forces, measurement noise, and sensor inaccuracies can overwhelm traditional control algorithms, leading to oscillatory behavior or steady-state errors that compromise system performance and reliability.
Time-varying dynamics represent another significant hurdle. Many industrial systems experience changes in their dynamic characteristics during operation, such as robotic manipulators handling variable payloads or chemical processes with temperature-dependent reaction rates. PID controllers with fixed parameters struggle to maintain consistent performance across these varying conditions, necessitating more sophisticated adaptive approaches.
The limitations of linear control theory become apparent when addressing nonlinear systems with uncertainty. Real-world systems frequently exhibit nonlinear behaviors that traditional PID formulations cannot adequately address, especially when these nonlinearities interact with system uncertainties in complex ways.
Implementation constraints further complicate robust PID design. Practical considerations such as actuator saturation, computational limitations in embedded systems, and sampling rate restrictions can severely impact controller performance. These constraints often necessitate compromises in controller design that further reduce robustness margins.
Theoretical frameworks for analyzing robustness, such as H-infinity and μ-synthesis, while powerful, remain challenging to apply in practical PID implementations. The gap between advanced robust control theory and practical PID tuning methods used in industry continues to be a significant obstacle to developing truly robust controllers for uncertain systems.
The integration of PID control with modern techniques like machine learning and adaptive control shows promise but introduces new challenges related to stability guarantees, computational requirements, and system identification under uncertainty. Bridging this gap represents one of the most pressing research directions in the field.
Parameter uncertainty presents a particularly vexing challenge, as real-world systems rarely match their mathematical models perfectly. Manufacturing variations, component aging, and environmental factors can cause system parameters to deviate significantly from nominal values. Conventional PID controllers, tuned for specific operating conditions, frequently exhibit degraded performance or even instability when these parameters drift beyond anticipated ranges.
Disturbance rejection capabilities of standard PID implementations are often insufficient for systems operating in harsh or unpredictable environments. External forces, measurement noise, and sensor inaccuracies can overwhelm traditional control algorithms, leading to oscillatory behavior or steady-state errors that compromise system performance and reliability.
Time-varying dynamics represent another significant hurdle. Many industrial systems experience changes in their dynamic characteristics during operation, such as robotic manipulators handling variable payloads or chemical processes with temperature-dependent reaction rates. PID controllers with fixed parameters struggle to maintain consistent performance across these varying conditions, necessitating more sophisticated adaptive approaches.
The limitations of linear control theory become apparent when addressing nonlinear systems with uncertainty. Real-world systems frequently exhibit nonlinear behaviors that traditional PID formulations cannot adequately address, especially when these nonlinearities interact with system uncertainties in complex ways.
Implementation constraints further complicate robust PID design. Practical considerations such as actuator saturation, computational limitations in embedded systems, and sampling rate restrictions can severely impact controller performance. These constraints often necessitate compromises in controller design that further reduce robustness margins.
Theoretical frameworks for analyzing robustness, such as H-infinity and μ-synthesis, while powerful, remain challenging to apply in practical PID implementations. The gap between advanced robust control theory and practical PID tuning methods used in industry continues to be a significant obstacle to developing truly robust controllers for uncertain systems.
The integration of PID control with modern techniques like machine learning and adaptive control shows promise but introduces new challenges related to stability guarantees, computational requirements, and system identification under uncertainty. Bridging this gap represents one of the most pressing research directions in the field.
State-of-the-Art Robust PID Design Approaches
01 Adaptive PID control for enhanced robustness
Adaptive PID controllers automatically adjust their parameters in response to changing process conditions, disturbances, or system dynamics. This self-tuning capability significantly improves robustness by maintaining optimal control performance across varying operating conditions. These controllers typically incorporate algorithms that continuously monitor system response and modify proportional, integral, and derivative gains accordingly, ensuring stability and performance even when faced with parameter uncertainties or external disturbances.- Adaptive PID control for robustness enhancement: Adaptive PID controllers can automatically adjust their parameters in response to changing process conditions, disturbances, or uncertainties. This adaptation mechanism enhances the robustness of the control system by maintaining performance despite variations in the controlled system. These controllers typically incorporate algorithms that monitor system behavior and modify PID gains accordingly, ensuring stability across a wide operating range.
- Robust PID tuning methods: Various tuning methodologies have been developed to enhance PID controller robustness against system uncertainties and disturbances. These methods focus on determining optimal controller parameters that provide a balance between performance and stability margins. Techniques include frequency-domain approaches, optimization-based tuning, and robust control theory applications that explicitly account for model uncertainties when setting PID parameters.
- Hybrid and advanced PID structures for improved robustness: Hybrid control structures that combine PID with other control techniques can significantly improve robustness. These approaches include fuzzy-PID controllers, neural network augmented PID systems, and model predictive control with PID elements. Such hybrid structures leverage the simplicity of PID while addressing its limitations through advanced control theory, resulting in systems that maintain stability and performance despite uncertainties and disturbances.
- Disturbance rejection techniques in PID control: Specialized PID controller designs focus on enhancing disturbance rejection capabilities to improve robustness. These techniques include disturbance observers, feed-forward compensation, and anti-windup mechanisms that prevent integral term saturation. By effectively handling external disturbances and system variations, these controllers maintain stable operation and performance even under challenging conditions, making the overall control system more robust.
- Stability analysis and robustness assessment methods: Various analytical and computational methods have been developed to assess and ensure the robustness of PID control systems. These include stability margin analysis, sensitivity function evaluation, and Monte Carlo simulations with parameter variations. Such methods provide quantitative measures of robustness, allowing engineers to verify controller performance across a range of operating conditions and system uncertainties before implementation.
02 Robust PID tuning methods
Various tuning methodologies have been developed to enhance PID controller robustness against system uncertainties and disturbances. These methods focus on finding optimal controller parameters that provide a balance between performance and stability margins. Techniques include frequency domain approaches, optimization-based tuning, and robust control theory applications. The goal is to ensure the controller maintains acceptable performance despite model inaccuracies, parameter variations, or operating condition changes.Expand Specific Solutions03 Hybrid and advanced PID architectures
Hybrid control systems combine PID with other control strategies to enhance robustness. These architectures may integrate fuzzy logic, neural networks, or model predictive control with traditional PID structures. The resulting controllers leverage the simplicity and reliability of PID while addressing its limitations through complementary techniques. Such hybrid approaches can significantly improve disturbance rejection, setpoint tracking, and overall system stability under uncertain conditions.Expand Specific Solutions04 Robustness analysis and validation techniques
Methods for analyzing and validating PID controller robustness ensure reliable performance under various operating conditions. These techniques include sensitivity analysis, Monte Carlo simulations, and worst-case scenario testing. By systematically evaluating controller behavior against parameter variations, disturbances, and model uncertainties, engineers can quantify robustness margins and make informed design decisions. This analysis helps identify potential weaknesses and optimize controller settings for maximum stability and performance.Expand Specific Solutions05 Industry-specific robust PID implementations
Specialized PID controller implementations address robustness requirements in specific industrial applications. These domain-specific designs consider unique challenges such as nonlinearities, time delays, or harsh operating environments found in power systems, manufacturing processes, or automotive applications. By tailoring the PID structure and parameters to the particular industry needs, these controllers achieve superior robustness while maintaining the simplicity and familiarity of the PID framework.Expand Specific Solutions
Leading Research Groups and Companies in Robust Control
The robust PID controller design for systems with uncertainty is currently in a growth phase, with an expanding market driven by increasing demand for reliable control systems across industries. The global market size is estimated to be over $2 billion, growing at approximately 5-7% annually. From a technological maturity perspective, academic institutions like Beihang University, Carnegie Mellon University, and South China University of Technology are leading fundamental research, while companies including ABB Patent GmbH, Robert Bosch GmbH, and IBM are developing practical industrial applications. Schweitzer Engineering Laboratories and Tokyo Electron are advancing specialized implementations for power systems and semiconductor manufacturing respectively. The competitive landscape shows a balanced distribution between academic research and industrial applications, with increasing collaboration between these sectors to address real-world uncertainty challenges.
Schweitzer Engineering Laboratories, Inc.
Technical Solution: Schweitzer Engineering Laboratories (SEL) has developed advanced adaptive PID control systems specifically designed for power systems with high uncertainty. Their approach combines traditional PID control with adaptive algorithms that automatically adjust controller parameters in real-time based on system identification techniques. SEL's robust PID controllers implement μ-synthesis and H-infinity optimization methods to guarantee stability margins across a wide range of operating conditions. Their controllers feature automatic parameter tuning capabilities that continuously estimate plant model parameters and adjust the control law accordingly. SEL has also integrated their robust PID solutions with their power system protection devices, creating a comprehensive control and protection ecosystem that maintains stability even during significant grid disturbances.
Strengths: Specialized expertise in power system applications with proven field reliability; seamless integration with existing protection infrastructure. Weaknesses: Solutions are primarily focused on power industry applications rather than general-purpose control systems; relatively higher implementation costs compared to conventional PID controllers.
International Business Machines Corp.
Technical Solution: IBM has developed advanced robust PID control systems leveraging their expertise in computational intelligence and optimization. Their approach utilizes robust optimization techniques to design PID controllers that maintain stability and performance across the entire uncertainty space. IBM's solution incorporates machine learning algorithms that continuously refine the uncertainty model based on operational data, allowing the controller to adapt to changing system characteristics. Their framework implements polynomial chaos expansion methods to efficiently propagate uncertainties through the control system and quantify their impact on performance metrics. For complex systems, IBM has developed distributed robust PID architectures that coordinate multiple controllers while maintaining global stability guarantees despite interconnection uncertainties. Their cloud-based implementation enables remote monitoring and optimization of controller performance, with automated parameter adjustment recommendations based on historical performance data and detected uncertainty patterns.
Strengths: Superior computational methods for uncertainty quantification and propagation; integration with broader AI and cloud infrastructure. Weaknesses: Solutions often require significant computational resources compared to traditional approaches; higher dependency on data quality and availability for optimal performance.
Key Theoretical Frameworks for Uncertainty Handling
Uncertainty system PID controller design method based on time-varying reliability
PatentActiveCN111352340A
Innovation
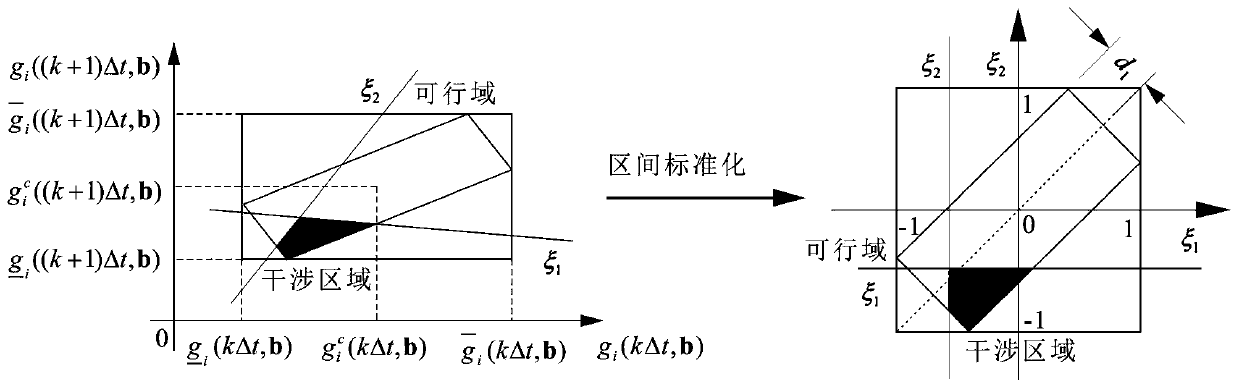
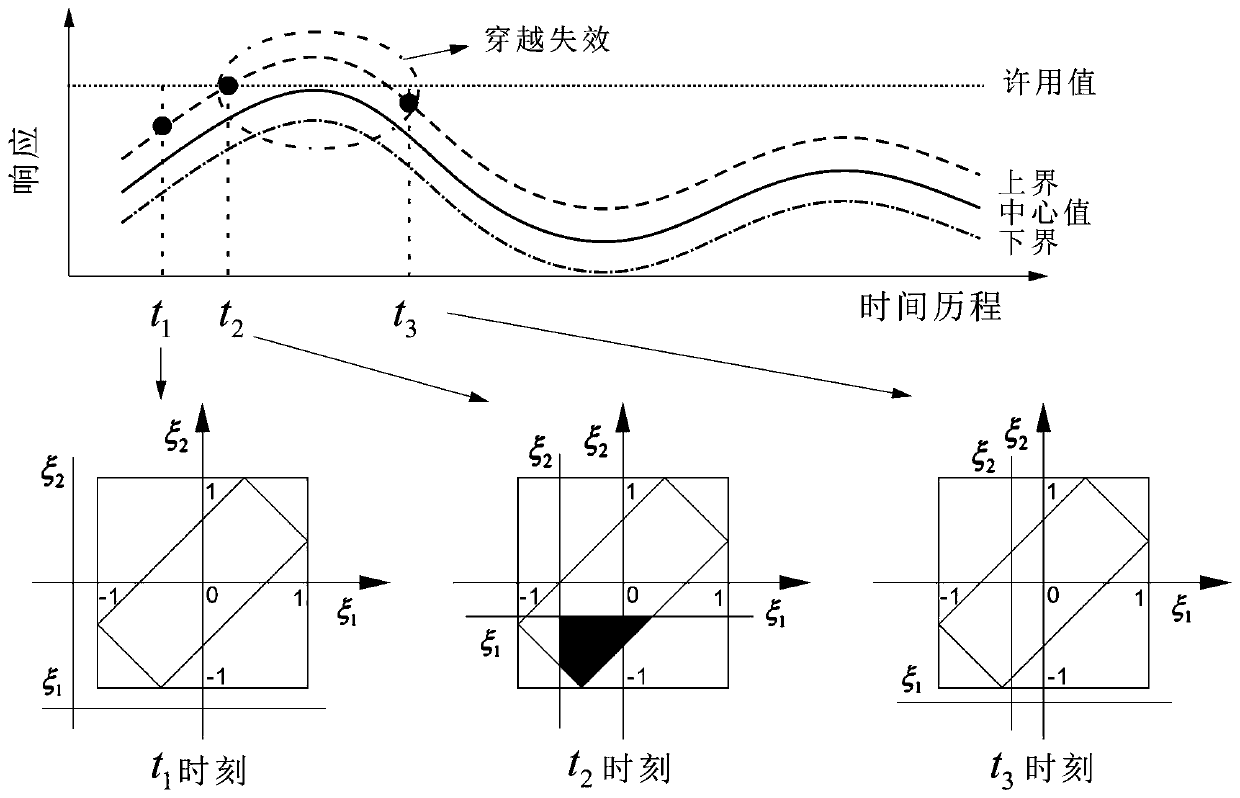
- The PID controller design method for uncertain systems based on time-varying reliability is used to describe the uncertain variables through non-probabilistic intervals, calculate the time-varying reliability, and use this to design the controller, and use the combination of the collocation method and the vertex method to solve the response. interval, combined with the first crossing theory to calculate the time-varying reliability, and iteratively optimize the PID parameters to meet the reliability requirements.
Performance Metrics and Validation Methods
Evaluating the effectiveness of robust PID controllers requires comprehensive performance metrics and rigorous validation methodologies. The stability margin serves as a fundamental metric, quantifying a controller's ability to maintain stability despite system uncertainties. This includes gain margin, phase margin, and modulus margin measurements that indicate how much parameter variation a system can tolerate before becoming unstable.
Robustness indices provide quantitative measures of a controller's resilience against uncertainties. The H∞ norm, structured singular value (μ), and sensitivity function analysis offer mathematical frameworks to assess performance degradation under various disturbance scenarios. These metrics enable engineers to compare different controller designs objectively and select optimal configurations for specific applications.
Time-domain performance criteria remain essential for practical implementation. Metrics such as settling time, rise time, and overshoot percentage must be evaluated across the entire uncertainty range rather than just at nominal operating points. Monte Carlo simulations with randomized parameter variations can generate statistical distributions of these performance indicators, providing a comprehensive view of expected controller behavior.
Frequency-domain analysis complements time-domain assessment by examining bandwidth limitations, resonance peaks, and disturbance rejection capabilities. Bode plots, Nyquist diagrams, and Nichols charts visualize how uncertainties affect system response across different frequencies, helping identify potential performance bottlenecks.
Validation methodologies must incorporate both simulation-based and experimental approaches. Hardware-in-the-loop testing bridges the gap between theoretical models and physical implementation by introducing actual system components into the validation process. This hybrid approach reveals practical limitations that purely mathematical models might overlook.
Robustness certification techniques, including formal verification methods and worst-case analysis, provide mathematical guarantees about controller performance. These approaches systematically explore the uncertainty space to identify critical scenarios that might compromise system stability or performance, ensuring that the controller meets specifications under all anticipated operating conditions.
Cross-validation between different modeling approaches enhances confidence in controller robustness. Comparing results from first-principles models, identified models, and empirical data helps detect inconsistencies and refine uncertainty characterizations. This multi-model validation strategy reduces the risk of overlooking critical system behaviors during the design phase.
Robustness indices provide quantitative measures of a controller's resilience against uncertainties. The H∞ norm, structured singular value (μ), and sensitivity function analysis offer mathematical frameworks to assess performance degradation under various disturbance scenarios. These metrics enable engineers to compare different controller designs objectively and select optimal configurations for specific applications.
Time-domain performance criteria remain essential for practical implementation. Metrics such as settling time, rise time, and overshoot percentage must be evaluated across the entire uncertainty range rather than just at nominal operating points. Monte Carlo simulations with randomized parameter variations can generate statistical distributions of these performance indicators, providing a comprehensive view of expected controller behavior.
Frequency-domain analysis complements time-domain assessment by examining bandwidth limitations, resonance peaks, and disturbance rejection capabilities. Bode plots, Nyquist diagrams, and Nichols charts visualize how uncertainties affect system response across different frequencies, helping identify potential performance bottlenecks.
Validation methodologies must incorporate both simulation-based and experimental approaches. Hardware-in-the-loop testing bridges the gap between theoretical models and physical implementation by introducing actual system components into the validation process. This hybrid approach reveals practical limitations that purely mathematical models might overlook.
Robustness certification techniques, including formal verification methods and worst-case analysis, provide mathematical guarantees about controller performance. These approaches systematically explore the uncertainty space to identify critical scenarios that might compromise system stability or performance, ensuring that the controller meets specifications under all anticipated operating conditions.
Cross-validation between different modeling approaches enhances confidence in controller robustness. Comparing results from first-principles models, identified models, and empirical data helps detect inconsistencies and refine uncertainty characterizations. This multi-model validation strategy reduces the risk of overlooking critical system behaviors during the design phase.
Real-world Implementation Considerations
Implementing robust PID controllers in real-world systems requires careful consideration of practical constraints that often differ significantly from theoretical models. Hardware limitations present a primary challenge, as computational resources may restrict the controller's sampling rate and complexity. Most industrial systems utilize embedded processors with limited memory and processing power, necessitating optimization of control algorithms. Additionally, sensor quality directly impacts control performance, with noise, resolution limitations, and sampling delays potentially degrading the controller's effectiveness.
Actuator constraints represent another critical consideration. Physical systems invariably face limitations such as saturation limits, rate constraints, and deadband regions that can lead to integral windup and performance deterioration. Implementing anti-windup mechanisms becomes essential to maintain controller stability when actuators reach their physical limits. Similarly, signal conditioning through appropriate filtering techniques must balance noise reduction against introducing unacceptable phase delays.
Environmental factors significantly influence controller performance in industrial settings. Temperature variations can affect sensor calibration and electronic component behavior, while electromagnetic interference may corrupt signals in manufacturing environments. Robust implementations must incorporate appropriate shielding, filtering, and calibration procedures to mitigate these effects. Furthermore, power supply fluctuations can introduce unexpected disturbances, requiring voltage regulation and protection circuits.
Safety considerations demand particular attention when implementing PID controllers in critical systems. Fail-safe mechanisms must be incorporated to ensure system stability during controller failures, often requiring redundant sensors, watchdog timers, and graceful degradation strategies. Regulatory compliance adds another layer of complexity, with industries such as aerospace, automotive, and medical devices subject to stringent certification requirements that influence implementation decisions.
Maintenance and operational requirements also shape implementation strategies. Systems must be designed for accessibility, with diagnostic capabilities that facilitate troubleshooting and parameter adjustment. User interfaces should allow non-specialist operators to monitor system performance without compromising safety or stability. Documentation of tuning parameters, system responses, and maintenance procedures becomes essential for long-term system viability.
Cost constraints inevitably influence implementation decisions, requiring careful balancing of performance requirements against budget limitations. While high-precision components may theoretically yield superior control, practical implementations must consider the diminishing returns of increased expenditure. This economic reality often drives the selection of appropriate sensors, actuators, and computational platforms, highlighting the importance of understanding the minimum requirements for achieving acceptable robust performance.
Actuator constraints represent another critical consideration. Physical systems invariably face limitations such as saturation limits, rate constraints, and deadband regions that can lead to integral windup and performance deterioration. Implementing anti-windup mechanisms becomes essential to maintain controller stability when actuators reach their physical limits. Similarly, signal conditioning through appropriate filtering techniques must balance noise reduction against introducing unacceptable phase delays.
Environmental factors significantly influence controller performance in industrial settings. Temperature variations can affect sensor calibration and electronic component behavior, while electromagnetic interference may corrupt signals in manufacturing environments. Robust implementations must incorporate appropriate shielding, filtering, and calibration procedures to mitigate these effects. Furthermore, power supply fluctuations can introduce unexpected disturbances, requiring voltage regulation and protection circuits.
Safety considerations demand particular attention when implementing PID controllers in critical systems. Fail-safe mechanisms must be incorporated to ensure system stability during controller failures, often requiring redundant sensors, watchdog timers, and graceful degradation strategies. Regulatory compliance adds another layer of complexity, with industries such as aerospace, automotive, and medical devices subject to stringent certification requirements that influence implementation decisions.
Maintenance and operational requirements also shape implementation strategies. Systems must be designed for accessibility, with diagnostic capabilities that facilitate troubleshooting and parameter adjustment. User interfaces should allow non-specialist operators to monitor system performance without compromising safety or stability. Documentation of tuning parameters, system responses, and maintenance procedures becomes essential for long-term system viability.
Cost constraints inevitably influence implementation decisions, requiring careful balancing of performance requirements against budget limitations. While high-precision components may theoretically yield superior control, practical implementations must consider the diminishing returns of increased expenditure. This economic reality often drives the selection of appropriate sensors, actuators, and computational platforms, highlighting the importance of understanding the minimum requirements for achieving acceptable robust performance.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!