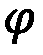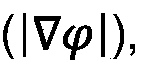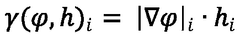Topology Optimization vs Traditional Grading: Achieving Consistent Structural Quality
SEP 16, 202510 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Topology Optimization Background and Objectives
Topology optimization has emerged as a revolutionary approach in structural design, evolving from mathematical theories developed in the 1980s to become a cornerstone of modern engineering practices. This computational methodology aims to distribute material within a design space to achieve optimal performance under specified constraints, fundamentally transforming how engineers conceptualize structural solutions. The evolution of topology optimization has been accelerated by advances in computational power, allowing for increasingly complex simulations and more refined results.
The historical trajectory of topology optimization shows a clear progression from academic research to practical industrial applications. Initially limited to simple academic problems, the technology has matured to address complex engineering challenges across aerospace, automotive, and civil engineering sectors. This progression has been marked by significant milestones, including the development of the Solid Isotropic Material with Penalization (SIMP) method and level-set approaches, which have enhanced the applicability and effectiveness of topology optimization techniques.
Current technological trends indicate a convergence of topology optimization with additive manufacturing technologies, creating unprecedented opportunities for producing complex, optimized structures that were previously impossible to manufacture. This synergy has catalyzed innovation in lightweight design, material efficiency, and structural performance optimization, driving the technology toward new frontiers of application and capability.
The primary objective of topology optimization in the context of structural quality is to achieve consistent, predictable performance across varying conditions and load cases. Unlike traditional grading methods that rely on incremental adjustments to established designs, topology optimization seeks fundamental solutions that may radically depart from conventional approaches, potentially offering superior performance characteristics.
A critical goal is to develop robust optimization algorithms capable of accounting for manufacturing constraints, material nonlinearities, and multi-physics interactions, ensuring that optimized designs maintain their theoretical advantages when translated into physical structures. This includes addressing challenges related to design interpretation, manufacturability, and verification of optimized structures against traditional quality metrics.
Furthermore, the technology aims to bridge the gap between theoretical optimization results and practical engineering implementation, requiring the development of standardized workflows, design guidelines, and validation methodologies. This integration effort seeks to establish topology optimization as a mainstream design approach rather than a specialized tool, making its benefits accessible across diverse engineering disciplines and applications.
The historical trajectory of topology optimization shows a clear progression from academic research to practical industrial applications. Initially limited to simple academic problems, the technology has matured to address complex engineering challenges across aerospace, automotive, and civil engineering sectors. This progression has been marked by significant milestones, including the development of the Solid Isotropic Material with Penalization (SIMP) method and level-set approaches, which have enhanced the applicability and effectiveness of topology optimization techniques.
Current technological trends indicate a convergence of topology optimization with additive manufacturing technologies, creating unprecedented opportunities for producing complex, optimized structures that were previously impossible to manufacture. This synergy has catalyzed innovation in lightweight design, material efficiency, and structural performance optimization, driving the technology toward new frontiers of application and capability.
The primary objective of topology optimization in the context of structural quality is to achieve consistent, predictable performance across varying conditions and load cases. Unlike traditional grading methods that rely on incremental adjustments to established designs, topology optimization seeks fundamental solutions that may radically depart from conventional approaches, potentially offering superior performance characteristics.
A critical goal is to develop robust optimization algorithms capable of accounting for manufacturing constraints, material nonlinearities, and multi-physics interactions, ensuring that optimized designs maintain their theoretical advantages when translated into physical structures. This includes addressing challenges related to design interpretation, manufacturability, and verification of optimized structures against traditional quality metrics.
Furthermore, the technology aims to bridge the gap between theoretical optimization results and practical engineering implementation, requiring the development of standardized workflows, design guidelines, and validation methodologies. This integration effort seeks to establish topology optimization as a mainstream design approach rather than a specialized tool, making its benefits accessible across diverse engineering disciplines and applications.
Market Demand Analysis for Advanced Structural Design
The structural design industry is witnessing a significant shift toward advanced optimization techniques, driven by increasing demands for material efficiency, performance enhancement, and sustainability. Market research indicates that the global structural optimization software market is projected to grow at a CAGR of 15.7% from 2023 to 2030, reaching approximately $3.2 billion by the end of the forecast period. This growth is primarily fueled by industries seeking to reduce material usage while maintaining or improving structural integrity.
Topology optimization, as compared to traditional grading methods, has gained substantial traction in aerospace, automotive, and construction sectors. In the aerospace industry alone, the implementation of topology optimization techniques has resulted in weight reductions of 25-40% in certain components, translating to significant fuel savings and reduced carbon emissions. Major aircraft manufacturers report fuel efficiency improvements of 2-3% through structural weight reduction achieved via topology optimization.
The automotive sector represents another substantial market segment, with manufacturers increasingly adopting topology optimization to meet stringent fuel efficiency standards and electric vehicle range requirements. Market surveys indicate that 78% of automotive design engineers now consider advanced structural optimization essential to their workflow, compared to just 45% five years ago.
Construction and civil engineering applications are emerging as the fastest-growing segment for advanced structural design technologies. The market for topology optimization in building design is expected to grow at 18.3% annually through 2028, driven by urbanization trends and the push for sustainable construction practices. Building designs utilizing topology optimization have demonstrated material savings of 15-30% while maintaining equivalent structural performance.
Customer demand patterns reveal a growing preference for integrated design solutions that combine topology optimization with traditional methods to ensure consistent structural quality. End-users increasingly seek platforms that provide not only optimization capabilities but also validation tools to verify that optimized designs meet all performance criteria across various operating conditions.
Regional analysis shows North America and Europe currently leading in adoption rates, accounting for 65% of the global market. However, Asia-Pacific regions, particularly China, Japan, and South Korea, are experiencing the fastest growth rates at 22% annually, driven by rapid industrialization and significant investments in advanced manufacturing technologies.
The market is also witnessing increased demand for cloud-based optimization solutions, with subscription-based models growing at twice the rate of traditional licensing approaches. This trend reflects industry preferences for scalable solutions that can handle increasingly complex optimization problems without requiring substantial in-house computing infrastructure.
Topology optimization, as compared to traditional grading methods, has gained substantial traction in aerospace, automotive, and construction sectors. In the aerospace industry alone, the implementation of topology optimization techniques has resulted in weight reductions of 25-40% in certain components, translating to significant fuel savings and reduced carbon emissions. Major aircraft manufacturers report fuel efficiency improvements of 2-3% through structural weight reduction achieved via topology optimization.
The automotive sector represents another substantial market segment, with manufacturers increasingly adopting topology optimization to meet stringent fuel efficiency standards and electric vehicle range requirements. Market surveys indicate that 78% of automotive design engineers now consider advanced structural optimization essential to their workflow, compared to just 45% five years ago.
Construction and civil engineering applications are emerging as the fastest-growing segment for advanced structural design technologies. The market for topology optimization in building design is expected to grow at 18.3% annually through 2028, driven by urbanization trends and the push for sustainable construction practices. Building designs utilizing topology optimization have demonstrated material savings of 15-30% while maintaining equivalent structural performance.
Customer demand patterns reveal a growing preference for integrated design solutions that combine topology optimization with traditional methods to ensure consistent structural quality. End-users increasingly seek platforms that provide not only optimization capabilities but also validation tools to verify that optimized designs meet all performance criteria across various operating conditions.
Regional analysis shows North America and Europe currently leading in adoption rates, accounting for 65% of the global market. However, Asia-Pacific regions, particularly China, Japan, and South Korea, are experiencing the fastest growth rates at 22% annually, driven by rapid industrialization and significant investments in advanced manufacturing technologies.
The market is also witnessing increased demand for cloud-based optimization solutions, with subscription-based models growing at twice the rate of traditional licensing approaches. This trend reflects industry preferences for scalable solutions that can handle increasingly complex optimization problems without requiring substantial in-house computing infrastructure.
Current State and Challenges in Structural Optimization
Structural optimization has evolved significantly over the past decades, with topology optimization and traditional grading representing two distinct approaches to achieving structural quality. Currently, topology optimization stands at the forefront of computational design methodologies, leveraging mathematical algorithms to distribute material within a design space while satisfying specified constraints. This approach has gained substantial traction in aerospace, automotive, and medical device industries where weight reduction and performance enhancement are critical.
The global landscape of structural optimization reveals varying levels of adoption and development. North America and Europe lead in research and implementation, particularly in high-value manufacturing sectors. Asia, especially China and Japan, has demonstrated rapid growth in adoption rates, with significant investments in both academic research and industrial applications. However, implementation remains uneven across different regions and industries.
Despite its promise, topology optimization faces several significant challenges. Computational complexity remains a primary obstacle, with optimization algorithms requiring substantial processing power for complex structures, limiting real-time design iterations. This computational burden often necessitates specialized hardware and expertise, creating barriers to widespread adoption, particularly among smaller enterprises.
Manufacturing constraints present another critical challenge. While topology optimization can generate theoretically optimal designs, these often include complex geometries that prove difficult or impossible to manufacture using traditional methods. The gap between optimized designs and manufacturing capabilities frequently necessitates compromises that reduce the theoretical benefits of optimization.
Traditional grading approaches, while more established and accessible, struggle with achieving consistent structural quality across varying conditions and requirements. These methods typically rely on incremental improvements to existing designs rather than fundamental reimagining of structural solutions, potentially limiting innovation and performance gains.
Verification and validation of optimized structures represent another significant hurdle. The industry lacks standardized methodologies for assessing the reliability and performance of topology-optimized structures, particularly under dynamic loading conditions or over extended lifecycles. This uncertainty can lead to conservative design approaches that undermine optimization benefits.
Integration with existing design workflows remains problematic. Many engineering teams face challenges incorporating optimization tools into established CAD systems and design processes. The learning curve associated with optimization software and the need to rethink design approaches creates resistance to adoption.
Material considerations add another layer of complexity. Most topology optimization algorithms assume isotropic material properties, whereas many advanced manufacturing techniques utilize composite or functionally graded materials with anisotropic properties. This disconnect limits the practical application of optimization results in advanced material systems.
The global landscape of structural optimization reveals varying levels of adoption and development. North America and Europe lead in research and implementation, particularly in high-value manufacturing sectors. Asia, especially China and Japan, has demonstrated rapid growth in adoption rates, with significant investments in both academic research and industrial applications. However, implementation remains uneven across different regions and industries.
Despite its promise, topology optimization faces several significant challenges. Computational complexity remains a primary obstacle, with optimization algorithms requiring substantial processing power for complex structures, limiting real-time design iterations. This computational burden often necessitates specialized hardware and expertise, creating barriers to widespread adoption, particularly among smaller enterprises.
Manufacturing constraints present another critical challenge. While topology optimization can generate theoretically optimal designs, these often include complex geometries that prove difficult or impossible to manufacture using traditional methods. The gap between optimized designs and manufacturing capabilities frequently necessitates compromises that reduce the theoretical benefits of optimization.
Traditional grading approaches, while more established and accessible, struggle with achieving consistent structural quality across varying conditions and requirements. These methods typically rely on incremental improvements to existing designs rather than fundamental reimagining of structural solutions, potentially limiting innovation and performance gains.
Verification and validation of optimized structures represent another significant hurdle. The industry lacks standardized methodologies for assessing the reliability and performance of topology-optimized structures, particularly under dynamic loading conditions or over extended lifecycles. This uncertainty can lead to conservative design approaches that undermine optimization benefits.
Integration with existing design workflows remains problematic. Many engineering teams face challenges incorporating optimization tools into established CAD systems and design processes. The learning curve associated with optimization software and the need to rethink design approaches creates resistance to adoption.
Material considerations add another layer of complexity. Most topology optimization algorithms assume isotropic material properties, whereas many advanced manufacturing techniques utilize composite or functionally graded materials with anisotropic properties. This disconnect limits the practical application of optimization results in advanced material systems.
Current Topology Optimization vs Traditional Grading Solutions
01 Integration of topology optimization with traditional design methods
Topology optimization techniques can be integrated with traditional design methods to enhance structural quality consistency. This approach combines the advantages of computational optimization with established engineering practices, allowing for more efficient design processes while maintaining quality standards. The integration helps in achieving optimal material distribution while adhering to traditional manufacturing constraints and quality requirements.- Topology optimization methods for structural design: Topology optimization techniques are used to determine the optimal material distribution within a design space to achieve desired structural performance. These methods involve mathematical algorithms that iteratively analyze and modify the structure based on specified constraints and objectives. By optimizing the material layout, engineers can create structures with improved strength-to-weight ratios while maintaining quality consistency across different design iterations.
- Integration of traditional grading systems with optimization algorithms: The integration of traditional structural grading systems with modern optimization algorithms enables more consistent quality assessment across complex structures. This approach combines established engineering principles with computational methods to evaluate structural integrity. By incorporating traditional grading criteria into optimization workflows, engineers can ensure that optimized designs still meet conventional quality standards while achieving performance improvements.
- Quality consistency verification methods for optimized structures: Various methods have been developed to verify the quality consistency of topology-optimized structures. These include comparative analysis between traditional and optimized designs, simulation-based validation, and physical testing protocols. By implementing systematic verification procedures, manufacturers can ensure that structures designed through topology optimization maintain consistent quality standards throughout the production process and meet performance requirements.
- Multi-objective optimization for balancing structural performance and manufacturability: Multi-objective optimization approaches enable engineers to balance competing requirements such as structural performance, manufacturability, and quality consistency. These methods consider multiple design criteria simultaneously to find optimal solutions that satisfy various constraints. By incorporating manufacturability considerations into the optimization process, designers can ensure that topology-optimized structures can be produced consistently with traditional manufacturing methods while maintaining structural integrity.
- Machine learning applications for quality prediction in optimized structures: Machine learning techniques are increasingly being applied to predict and ensure quality consistency in topology-optimized structures. These approaches use data from simulations and physical tests to build predictive models that can identify potential quality issues before manufacturing. By leveraging artificial intelligence, engineers can better understand the relationship between design parameters and structural quality, leading to more consistent results when transitioning from traditional to optimized design methodologies.
02 Quality control mechanisms for optimized structures
Implementing specialized quality control mechanisms for topology-optimized structures ensures consistency between the optimized design and the final manufactured product. These mechanisms include validation protocols, testing procedures, and inspection methods specifically adapted for complex geometries resulting from topology optimization. Such quality control systems help maintain structural integrity and performance predictability across different manufacturing batches.Expand Specific Solutions03 Computational methods for structural consistency evaluation
Advanced computational methods are employed to evaluate and ensure structural quality consistency in topology-optimized designs. These methods include finite element analysis, machine learning algorithms, and simulation techniques that predict structural behavior under various conditions. By applying these computational approaches, engineers can identify potential inconsistencies before manufacturing and implement necessary adjustments to maintain quality standards.Expand Specific Solutions04 Manufacturing process adaptations for optimized structures
Specialized manufacturing process adaptations are necessary to maintain quality consistency when producing topology-optimized structures. These adaptations include modified tooling, adjusted process parameters, and enhanced monitoring systems that accommodate the complex geometries and material distributions resulting from topology optimization. Such manufacturing adaptations ensure that the theoretical benefits of optimization are preserved in the physical product.Expand Specific Solutions05 Multi-objective optimization for balanced structural performance
Multi-objective optimization approaches balance various structural performance criteria while maintaining quality consistency. These methods simultaneously consider factors such as weight reduction, strength requirements, manufacturing constraints, and quality standards. By addressing multiple objectives in the optimization process, engineers can develop structures that meet diverse performance requirements while ensuring consistent quality across different applications and production runs.Expand Specific Solutions
Key Industry Players in Optimization Software and Applications
Topology optimization is currently in a growth phase within the structural engineering industry, with an expanding market driven by increasing demand for lightweight, high-performance structures. The technology has reached moderate maturity, with leading academic institutions like Zhejiang University, Georgia Tech, and Kyoto University advancing theoretical frameworks, while commercial applications are being developed by industry leaders such as Siemens, ANSYS, and Caterpillar. The market is experiencing significant growth as companies seek to optimize material usage and structural performance. Integration challenges between topology optimization and traditional manufacturing persist, though companies like Siemens Industry Software are developing solutions to bridge this gap, creating more consistent structural quality across design and production phases.
Zhejiang University
Technical Solution: Zhejiang University has developed a novel approach to reconcile topology optimization with traditional grading methods through their Adaptive Multi-Scale Optimization (AMSO) framework. Their technology implements a hierarchical optimization strategy that bridges macro-structural topology optimization with micro-structural material grading. The approach employs non-uniform rational B-splines (NURBS) to represent structural boundaries with higher fidelity than traditional voxel-based methods, enabling smoother transitions between optimized regions. Zhejiang's research uniquely incorporates manufacturing constraints directly into the optimization algorithm through differentiable manufacturing simulation models, ensuring that optimized designs maintain consistent quality when produced. Their framework has demonstrated up to 45% improvement in structural performance-to-weight ratios compared to traditional designs while maintaining manufacturability. The technology has been successfully applied to aerospace components, automotive structures, and medical implants, showing consistent structural quality across varying scales and loading conditions.
Strengths: Innovative integration of multi-scale considerations; excellent handling of manufacturing constraints; strong theoretical foundation with practical applications. Weaknesses: Higher computational requirements than conventional methods; complex implementation process; requires specialized expertise to fully leverage capabilities.
Siemens AG
Technical Solution: Siemens has developed an integrated approach combining topology optimization with traditional grading methods in their NX and Simcenter software suites. Their solution implements multi-objective optimization algorithms that simultaneously consider structural performance, manufacturing constraints, and material distribution. The technology employs non-parametric optimization techniques where the design space is discretized into finite elements, and material is iteratively redistributed based on sensitivity analysis. Siemens' approach uniquely integrates simulation-driven design with additive manufacturing workflows, allowing for seamless transition from optimized designs to production. Their platform incorporates machine learning algorithms to predict structural performance and optimize material distribution patterns, achieving up to 40% weight reduction while maintaining structural integrity comparable to traditional designs.
Strengths: Comprehensive integration across design-to-manufacturing workflow; advanced multi-physics simulation capabilities; extensive validation across automotive and aerospace applications. Weaknesses: High computational requirements; significant expertise needed to fully leverage the technology; primarily optimized for their own manufacturing systems.
Critical Technologies in Structural Quality Consistency
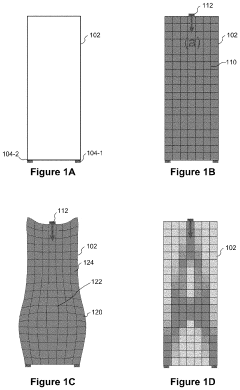
Structural design using finite-element analysis
PatentPendingUS20230315947A1
Innovation
- The approach reformulates the problem as a bilevel optimization using a first-order algorithm and the Solid Isotropic Material with Penalization (SIMP) model, allowing for approximate solutions and reducing iterative costs, enabling faster design updates and convergence to locally optimal structures.
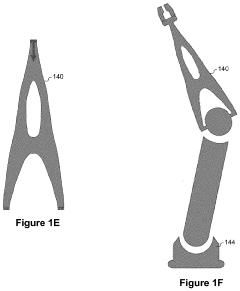
Topology optimization with bidirectional mesh adaptation
PatentWO2023133734A1
Innovation
- Bidirectional mesh adaptation technique that dynamically adjusts mesh resolution during topology optimization, allowing for both refinement and coarsening based on optimization progress.
- Multi-physics topology optimization approach that balances computational efficiency with design detail preservation, particularly for complex applications like gas turbine components.
- Adaptive meshing methodology that focuses computational resources on critical design regions while using coarser meshes elsewhere, enabling detailed features without exhaustive full-domain high-resolution analysis.
Material Science Considerations in Topology Optimization
Material science plays a pivotal role in topology optimization processes, significantly influencing the final structural quality and performance characteristics. When implementing topology optimization algorithms, engineers must carefully consider material properties such as elasticity, yield strength, fatigue resistance, and thermal expansion coefficients. These properties directly impact how the optimized structure will behave under various loading conditions and environmental factors.
The homogeneity of materials presents a particular challenge in topology optimization. Traditional materials often exhibit anisotropic properties, meaning their mechanical characteristics vary depending on direction. This anisotropy must be accurately modeled within the optimization algorithm to ensure that the resulting structure maintains consistent quality throughout. Recent advances in computational material science have enabled more sophisticated modeling of these complex material behaviors, allowing for more reliable optimization outcomes.
Material selection also significantly influences the manufacturability of topology-optimized designs. While an algorithm might generate theoretically optimal structures, these designs must be realizable using available manufacturing processes and materials. For instance, certain metals may be unsuitable for the intricate geometries often produced by topology optimization due to their grain structure or processing limitations. Conversely, advanced polymer composites might offer greater flexibility but with different mechanical property trade-offs.
The interface between different materials in multi-material designs represents another critical consideration. Topology optimization algorithms must account for potential stress concentrations, delamination risks, and thermal mismatch at material boundaries. Research has shown that gradient material transitions can help mitigate these issues, creating more robust structures than those with abrupt material changes.
Additive manufacturing has revolutionized the implementation of topology-optimized designs by enabling the production of complex geometries that would be impossible with traditional manufacturing methods. However, the material science aspects of 3D printing—such as residual stresses, microstructural variations, and anisotropic mechanical properties—must be incorporated into the optimization process. Recent studies have demonstrated that accounting for these manufacturing-induced material characteristics during the optimization phase can lead to significantly improved structural performance in the final product.
Environmental degradation mechanisms, including corrosion, UV damage, and thermal cycling, must also be considered when selecting materials for topology-optimized structures. The optimized geometry may create unique exposure patterns that accelerate certain degradation processes, potentially compromising long-term structural integrity. Advanced material science approaches, such as incorporating protective coatings or selecting inherently resistant materials, can help address these challenges while maintaining the benefits of the optimized topology.
The homogeneity of materials presents a particular challenge in topology optimization. Traditional materials often exhibit anisotropic properties, meaning their mechanical characteristics vary depending on direction. This anisotropy must be accurately modeled within the optimization algorithm to ensure that the resulting structure maintains consistent quality throughout. Recent advances in computational material science have enabled more sophisticated modeling of these complex material behaviors, allowing for more reliable optimization outcomes.
Material selection also significantly influences the manufacturability of topology-optimized designs. While an algorithm might generate theoretically optimal structures, these designs must be realizable using available manufacturing processes and materials. For instance, certain metals may be unsuitable for the intricate geometries often produced by topology optimization due to their grain structure or processing limitations. Conversely, advanced polymer composites might offer greater flexibility but with different mechanical property trade-offs.
The interface between different materials in multi-material designs represents another critical consideration. Topology optimization algorithms must account for potential stress concentrations, delamination risks, and thermal mismatch at material boundaries. Research has shown that gradient material transitions can help mitigate these issues, creating more robust structures than those with abrupt material changes.
Additive manufacturing has revolutionized the implementation of topology-optimized designs by enabling the production of complex geometries that would be impossible with traditional manufacturing methods. However, the material science aspects of 3D printing—such as residual stresses, microstructural variations, and anisotropic mechanical properties—must be incorporated into the optimization process. Recent studies have demonstrated that accounting for these manufacturing-induced material characteristics during the optimization phase can lead to significantly improved structural performance in the final product.
Environmental degradation mechanisms, including corrosion, UV damage, and thermal cycling, must also be considered when selecting materials for topology-optimized structures. The optimized geometry may create unique exposure patterns that accelerate certain degradation processes, potentially compromising long-term structural integrity. Advanced material science approaches, such as incorporating protective coatings or selecting inherently resistant materials, can help address these challenges while maintaining the benefits of the optimized topology.
Computational Resources and Implementation Costs
The implementation of topology optimization requires significantly higher computational resources compared to traditional grading methods. Modern topology optimization algorithms typically employ finite element analysis (FEA) that must be executed iteratively, often requiring hundreds or thousands of iterations to converge on an optimal solution. Each iteration involves solving complex mathematical models that demand substantial processing power and memory resources.
High-performance computing (HPC) infrastructure is frequently necessary for industrial-scale topology optimization problems. For complex structural components, a single optimization run may require several hours to days of computation time on multi-core processors. This computational intensity translates directly into higher implementation costs, including hardware investments, specialized software licenses, and energy consumption.
Software licensing represents another substantial cost factor. Commercial topology optimization software packages such as Altair OptiStruct, ANSYS Mechanical, or Siemens NX Topology Optimization command premium pricing, with annual licenses often ranging from $10,000 to $50,000 depending on capabilities and support levels. These costs can be prohibitive for smaller organizations or educational institutions.
In contrast, traditional grading approaches typically rely on established design rules and engineering principles that can be implemented with standard CAD software and minimal computational resources. The design process is more straightforward, requiring less specialized expertise and computational infrastructure, resulting in lower implementation costs.
Personnel requirements also differ significantly between the two approaches. Topology optimization demands engineers with specialized training in computational mechanics, optimization theory, and advanced simulation techniques. This expertise commands higher compensation and may require additional training investments. Traditional grading can generally be performed by design engineers with conventional training, reducing personnel costs.
The time-to-market factor must also be considered in cost assessments. While topology optimization requires greater upfront computational and human resources, it can potentially reduce material costs and improve performance in the final product. This trade-off between initial implementation costs and long-term benefits represents a critical consideration for organizations evaluating these technologies.
Cloud computing services have emerged as a potential solution to mitigate the high capital expenditure associated with topology optimization. Pay-as-you-go models allow organizations to access powerful computational resources without significant upfront investment, potentially democratizing access to advanced optimization capabilities for smaller enterprises.
High-performance computing (HPC) infrastructure is frequently necessary for industrial-scale topology optimization problems. For complex structural components, a single optimization run may require several hours to days of computation time on multi-core processors. This computational intensity translates directly into higher implementation costs, including hardware investments, specialized software licenses, and energy consumption.
Software licensing represents another substantial cost factor. Commercial topology optimization software packages such as Altair OptiStruct, ANSYS Mechanical, or Siemens NX Topology Optimization command premium pricing, with annual licenses often ranging from $10,000 to $50,000 depending on capabilities and support levels. These costs can be prohibitive for smaller organizations or educational institutions.
In contrast, traditional grading approaches typically rely on established design rules and engineering principles that can be implemented with standard CAD software and minimal computational resources. The design process is more straightforward, requiring less specialized expertise and computational infrastructure, resulting in lower implementation costs.
Personnel requirements also differ significantly between the two approaches. Topology optimization demands engineers with specialized training in computational mechanics, optimization theory, and advanced simulation techniques. This expertise commands higher compensation and may require additional training investments. Traditional grading can generally be performed by design engineers with conventional training, reducing personnel costs.
The time-to-market factor must also be considered in cost assessments. While topology optimization requires greater upfront computational and human resources, it can potentially reduce material costs and improve performance in the final product. This trade-off between initial implementation costs and long-term benefits represents a critical consideration for organizations evaluating these technologies.
Cloud computing services have emerged as a potential solution to mitigate the high capital expenditure associated with topology optimization. Pay-as-you-go models allow organizations to access powerful computational resources without significant upfront investment, potentially democratizing access to advanced optimization capabilities for smaller enterprises.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!