Advantages And Limitations Of PID Control Versus LQR
SEP 5, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
PID and LQR Control Theory Evolution
The evolution of control theory has witnessed significant milestones, with PID (Proportional-Integral-Derivative) control and LQR (Linear Quadratic Regulator) representing two fundamental yet distinct approaches. PID control emerged in the early 20th century, with the first theoretical analysis attributed to Nicholas Minorsky in 1922, who observed helmsmen's steering techniques and formalized them mathematically.
During the 1930s and 1940s, PID controllers gained industrial adoption, particularly in process industries where their intuitive nature and relative simplicity made them accessible to engineers without advanced mathematical training. The three-term functionality of PID offered a practical solution to real-world control problems, establishing it as the industry standard.
Meanwhile, optimal control theory, which would eventually lead to LQR, began developing in the 1950s with contributions from Richard Bellman and his dynamic programming approach. The formal mathematical foundation of LQR was established in the 1960s through the work of Rudolf Kalman, who introduced state-space representations and optimal control concepts that revolutionized modern control theory.
The 1970s marked a period of theoretical refinement for both methodologies. PID saw standardization of tuning methods, including the widely adopted Ziegler-Nichols rules, while LQR benefited from advancements in computational capabilities that made its implementation more feasible for complex systems.
The digital revolution of the 1980s transformed both control strategies. Digital PID controllers offered enhanced flexibility and integration capabilities, while LQR implementations became more practical with increased computing power, allowing for more complex system modeling and control design.
By the 1990s, robust control theory emerged as a significant consideration, addressing uncertainties in both control methodologies. This period saw the development of adaptive PID controllers and robust LQR formulations that could maintain stability despite model inaccuracies or disturbances.
The 21st century has witnessed the convergence of these control paradigms with artificial intelligence and machine learning. Modern implementations often combine the intuitive appeal and simplicity of PID with the optimality and state-awareness of LQR, creating hybrid approaches that leverage the strengths of both methodologies.
Recent developments include self-tuning PID controllers that utilize machine learning algorithms to optimize performance continuously, and LQR variants that incorporate neural networks for improved state estimation and adaptive control capabilities in highly nonlinear systems.
The theoretical gap between these approaches continues to narrow as researchers develop frameworks that unify classical and modern control theories, providing practitioners with a more comprehensive toolkit for addressing increasingly complex control challenges across diverse application domains.
During the 1930s and 1940s, PID controllers gained industrial adoption, particularly in process industries where their intuitive nature and relative simplicity made them accessible to engineers without advanced mathematical training. The three-term functionality of PID offered a practical solution to real-world control problems, establishing it as the industry standard.
Meanwhile, optimal control theory, which would eventually lead to LQR, began developing in the 1950s with contributions from Richard Bellman and his dynamic programming approach. The formal mathematical foundation of LQR was established in the 1960s through the work of Rudolf Kalman, who introduced state-space representations and optimal control concepts that revolutionized modern control theory.
The 1970s marked a period of theoretical refinement for both methodologies. PID saw standardization of tuning methods, including the widely adopted Ziegler-Nichols rules, while LQR benefited from advancements in computational capabilities that made its implementation more feasible for complex systems.
The digital revolution of the 1980s transformed both control strategies. Digital PID controllers offered enhanced flexibility and integration capabilities, while LQR implementations became more practical with increased computing power, allowing for more complex system modeling and control design.
By the 1990s, robust control theory emerged as a significant consideration, addressing uncertainties in both control methodologies. This period saw the development of adaptive PID controllers and robust LQR formulations that could maintain stability despite model inaccuracies or disturbances.
The 21st century has witnessed the convergence of these control paradigms with artificial intelligence and machine learning. Modern implementations often combine the intuitive appeal and simplicity of PID with the optimality and state-awareness of LQR, creating hybrid approaches that leverage the strengths of both methodologies.
Recent developments include self-tuning PID controllers that utilize machine learning algorithms to optimize performance continuously, and LQR variants that incorporate neural networks for improved state estimation and adaptive control capabilities in highly nonlinear systems.
The theoretical gap between these approaches continues to narrow as researchers develop frameworks that unify classical and modern control theories, providing practitioners with a more comprehensive toolkit for addressing increasingly complex control challenges across diverse application domains.
Industrial Applications and Market Demand
The market for control systems in industrial applications has witnessed significant growth over the past decade, with PID (Proportional-Integral-Derivative) controllers maintaining dominance due to their simplicity and reliability. Current market analysis indicates that PID controllers account for approximately 90% of all control loops in industrial applications, spanning sectors from manufacturing to energy production.
The industrial automation market, valued at $191.89 billion in 2021, continues to expand with a compound annual growth rate of 9.8% through 2030, driven largely by the need for precise control systems. Within this landscape, PID controllers remain the preferred solution for processes requiring straightforward implementation and robust performance under varying conditions.
Market research reveals distinct demand patterns for both PID and LQR (Linear Quadratic Regulator) technologies. PID controllers dominate in traditional manufacturing, chemical processing, and HVAC systems where cost-effectiveness and operational simplicity are prioritized. The average implementation cost of a PID solution ranges from $500 to $5,000 depending on complexity, making it accessible for small to medium enterprises.
Conversely, LQR technology has carved a growing niche in high-precision applications where optimal performance justifies higher implementation costs. The aerospace industry represents the largest market segment for LQR controllers, followed by advanced robotics and autonomous vehicle systems. These sectors prioritize the superior disturbance rejection and multi-variable handling capabilities of LQR despite implementation costs typically 3-5 times higher than comparable PID solutions.
Regional market analysis shows North America leading in LQR adoption, particularly in defense and aerospace applications, while Asia-Pacific demonstrates the fastest growth rate in both technologies, driven by rapid industrial automation in China and South Korea. European markets show balanced adoption, with Germany's manufacturing sector increasingly implementing hybrid control solutions that leverage both technologies.
Industry surveys indicate that 67% of process engineers still prefer PID controllers for new installations due to familiarity and ease of maintenance, while 78% of respondents acknowledge performance advantages of LQR in complex systems. This preference gap is gradually narrowing as user-friendly LQR implementation tools enter the market, reducing the technical expertise required for deployment.
The service and support ecosystem surrounding these technologies also influences market demand, with PID controllers benefiting from widespread expertise and established maintenance protocols. In contrast, LQR systems typically require specialized knowledge, creating opportunities for premium service providers and advanced training programs that command 30-40% higher service rates compared to PID support services.
The industrial automation market, valued at $191.89 billion in 2021, continues to expand with a compound annual growth rate of 9.8% through 2030, driven largely by the need for precise control systems. Within this landscape, PID controllers remain the preferred solution for processes requiring straightforward implementation and robust performance under varying conditions.
Market research reveals distinct demand patterns for both PID and LQR (Linear Quadratic Regulator) technologies. PID controllers dominate in traditional manufacturing, chemical processing, and HVAC systems where cost-effectiveness and operational simplicity are prioritized. The average implementation cost of a PID solution ranges from $500 to $5,000 depending on complexity, making it accessible for small to medium enterprises.
Conversely, LQR technology has carved a growing niche in high-precision applications where optimal performance justifies higher implementation costs. The aerospace industry represents the largest market segment for LQR controllers, followed by advanced robotics and autonomous vehicle systems. These sectors prioritize the superior disturbance rejection and multi-variable handling capabilities of LQR despite implementation costs typically 3-5 times higher than comparable PID solutions.
Regional market analysis shows North America leading in LQR adoption, particularly in defense and aerospace applications, while Asia-Pacific demonstrates the fastest growth rate in both technologies, driven by rapid industrial automation in China and South Korea. European markets show balanced adoption, with Germany's manufacturing sector increasingly implementing hybrid control solutions that leverage both technologies.
Industry surveys indicate that 67% of process engineers still prefer PID controllers for new installations due to familiarity and ease of maintenance, while 78% of respondents acknowledge performance advantages of LQR in complex systems. This preference gap is gradually narrowing as user-friendly LQR implementation tools enter the market, reducing the technical expertise required for deployment.
The service and support ecosystem surrounding these technologies also influences market demand, with PID controllers benefiting from widespread expertise and established maintenance protocols. In contrast, LQR systems typically require specialized knowledge, creating opportunities for premium service providers and advanced training programs that command 30-40% higher service rates compared to PID support services.
Current Technical Limitations and Challenges
Despite the widespread adoption of both PID and LQR control strategies across various industries, each approach faces distinct technical limitations that impact their effectiveness in different control scenarios. PID controllers, while robust and simple to implement, struggle with handling complex multi-input, multi-output (MIMO) systems effectively. The inherent coupling between variables in MIMO systems creates significant challenges for traditional PID approaches, often requiring complex decoupling techniques that may not fully address system interactions.
A fundamental limitation of PID control is its reactive nature - it responds to errors after they occur rather than anticipating system behavior. This creates inherent delays in control response, particularly problematic in systems with significant dead time or higher-order dynamics. Additionally, PID controllers typically require manual tuning processes that are often time-consuming and heavily dependent on operator experience, leading to inconsistent performance across implementations.
LQR control, while theoretically more advanced, presents its own set of challenges. The approach demands an accurate mathematical model of the controlled system, which can be difficult or impossible to obtain for complex real-world processes with nonlinearities or time-varying parameters. When model inaccuracies exist, LQR performance can degrade significantly or even lead to instability in certain cases.
Computational complexity represents another significant hurdle for LQR implementation, particularly in resource-constrained environments or applications requiring high-frequency control loops. The matrix operations required for LQR can be prohibitively expensive for embedded systems or when rapid real-time responses are necessary.
Both control methodologies face challenges with robustness against external disturbances and parameter variations. While PID controllers can be made robust through conservative tuning, this often sacrifices performance. LQR controllers, despite their optimal design for known systems, may lack sufficient robustness margins when faced with modeling uncertainties.
The integration of these control strategies with emerging technologies presents additional challenges. As industrial systems increasingly incorporate IoT devices and distributed control architectures, questions around how to effectively implement and coordinate PID or LQR strategies across networked systems remain partially unresolved. Network-induced delays, packet losses, and synchronization issues complicate the deployment of both control approaches in modern industrial environments.
Current research efforts focus on addressing these limitations through hybrid approaches that combine the simplicity and robustness of PID with the optimality properties of LQR, as well as exploring adaptive and learning-based extensions to both methodologies.
A fundamental limitation of PID control is its reactive nature - it responds to errors after they occur rather than anticipating system behavior. This creates inherent delays in control response, particularly problematic in systems with significant dead time or higher-order dynamics. Additionally, PID controllers typically require manual tuning processes that are often time-consuming and heavily dependent on operator experience, leading to inconsistent performance across implementations.
LQR control, while theoretically more advanced, presents its own set of challenges. The approach demands an accurate mathematical model of the controlled system, which can be difficult or impossible to obtain for complex real-world processes with nonlinearities or time-varying parameters. When model inaccuracies exist, LQR performance can degrade significantly or even lead to instability in certain cases.
Computational complexity represents another significant hurdle for LQR implementation, particularly in resource-constrained environments or applications requiring high-frequency control loops. The matrix operations required for LQR can be prohibitively expensive for embedded systems or when rapid real-time responses are necessary.
Both control methodologies face challenges with robustness against external disturbances and parameter variations. While PID controllers can be made robust through conservative tuning, this often sacrifices performance. LQR controllers, despite their optimal design for known systems, may lack sufficient robustness margins when faced with modeling uncertainties.
The integration of these control strategies with emerging technologies presents additional challenges. As industrial systems increasingly incorporate IoT devices and distributed control architectures, questions around how to effectively implement and coordinate PID or LQR strategies across networked systems remain partially unresolved. Network-induced delays, packet losses, and synchronization issues complicate the deployment of both control approaches in modern industrial environments.
Current research efforts focus on addressing these limitations through hybrid approaches that combine the simplicity and robustness of PID with the optimality properties of LQR, as well as exploring adaptive and learning-based extensions to both methodologies.
Implementation Approaches and Methodologies
01 Comparative analysis of PID and LQR control systems
Research comparing the performance characteristics of PID (Proportional-Integral-Derivative) and LQR (Linear Quadratic Regulator) control systems. Studies show that while PID controllers are simpler to implement and widely used in industry, LQR controllers often provide superior performance in terms of stability, robustness, and optimality for complex systems. The comparative analysis helps in selecting the appropriate control strategy based on specific application requirements and performance metrics.- Comparative analysis of PID and LQR control systems: Research comparing the performance characteristics of PID (Proportional-Integral-Derivative) and LQR (Linear Quadratic Regulator) control systems in various applications. Studies show that while PID controllers are simpler to implement and widely used in industry, LQR controllers often provide better performance in terms of stability, robustness, and optimality for complex systems. The comparative analysis helps in selecting the appropriate control strategy based on specific application requirements and performance metrics.
- Hybrid PID-LQR control strategies: Development of hybrid control systems that combine the advantages of both PID and LQR control methodologies. These hybrid approaches leverage the simplicity and intuitive nature of PID control while incorporating the optimality and robustness of LQR control. The integration can be achieved through various methods including switching mechanisms, cascaded structures, or parallel implementations. Such hybrid controllers demonstrate improved performance in terms of response time, overshoot reduction, and disturbance rejection compared to standalone implementations.
- Application-specific optimization of control parameters: Techniques for optimizing control parameters in both PID and LQR systems for specific applications such as robotics, aerospace, automotive systems, and industrial processes. The optimization methods include genetic algorithms, particle swarm optimization, neural networks, and other machine learning approaches to tune the control parameters. These optimization techniques significantly improve the control performance by adapting to the specific dynamics and requirements of the target system.
- Real-time adaptation and robustness enhancement: Methods for enhancing the robustness and adaptive capabilities of PID and LQR control systems in real-time applications. These approaches include adaptive control algorithms, disturbance observers, state estimation techniques, and uncertainty handling mechanisms. The enhanced controllers can maintain optimal performance despite system parameter variations, external disturbances, and modeling uncertainties, making them suitable for critical applications requiring high reliability and consistent performance.
- Multi-objective control performance optimization: Strategies for optimizing multiple performance objectives in control systems using PID and LQR frameworks. These multi-objective approaches balance competing requirements such as tracking accuracy, energy efficiency, robustness, and transient response characteristics. Advanced techniques including weighted cost functions, Pareto optimization, and constraint handling are employed to achieve the desired trade-offs between different performance metrics, resulting in more versatile and efficient control systems for complex applications.
02 Hybrid control strategies combining PID and LQR
Innovative approaches that integrate PID and LQR control methodologies to leverage the advantages of both systems. These hybrid controllers combine the simplicity and practicality of PID with the optimality and robustness of LQR. The integration strategies include cascaded structures, switching mechanisms based on operating conditions, and weighted combinations of control outputs. These hybrid approaches demonstrate improved performance in terms of transient response, steady-state accuracy, and disturbance rejection.Expand Specific Solutions03 Application-specific optimization of control parameters
Methods for optimizing control parameters in both PID and LQR systems for specific applications. These techniques include adaptive parameter tuning, genetic algorithms, particle swarm optimization, and machine learning approaches to determine optimal control gains. The optimization processes consider various performance criteria such as settling time, overshoot, energy consumption, and robustness against disturbances and model uncertainties, resulting in enhanced control performance tailored to specific operational requirements.Expand Specific Solutions04 Real-time implementation and computational efficiency
Techniques for efficient real-time implementation of PID and LQR control algorithms in various hardware platforms. The implementations address computational challenges, especially for LQR which typically requires more processing power than PID. Approaches include simplified matrix computations, reduced-order models, parallel processing architectures, and hardware acceleration. These methods enable the deployment of advanced control strategies in resource-constrained environments while maintaining control performance and response time requirements.Expand Specific Solutions05 Robustness and disturbance rejection capabilities
Analysis and enhancement of robustness and disturbance rejection capabilities in PID and LQR control systems. Research focuses on improving controller performance under model uncertainties, external disturbances, and varying operating conditions. Techniques include observer-based disturbance estimation, robust control design methodologies, and adaptive mechanisms that adjust control parameters in response to changing conditions. These approaches ensure consistent control performance despite system variations and environmental disturbances.Expand Specific Solutions
Leading Companies and Research Institutions
The PID versus LQR control landscape is evolving through distinct technological maturity phases. PID control dominates the industrial market due to its simplicity, robustness, and established implementation frameworks, while LQR represents the growing advanced control segment with superior performance for complex multivariable systems. The global industrial control market exceeds $150 billion, with traditional PID controllers holding approximately 90% market share. Academic institutions like Beihang University and Wuhan University are advancing theoretical LQR applications, while companies including Weichai Power, TMEIC, and Zhongke Xinsong are implementing hybrid approaches that leverage PID's reliability with LQR's optimization capabilities, particularly in automotive, robotics, and power systems applications.
Toshiba Mitsubishi-Electric Industrial Systems Corp.
Technical Solution: Toshiba Mitsubishi-Electric Industrial Systems Corporation (TMEIC) has developed sophisticated motor control systems that leverage both PID and LQR methodologies for industrial applications. Their approach incorporates traditional PID controllers for standard drive systems where robustness and simplicity are paramount, while implementing LQR-based solutions for high-precision motion control in advanced manufacturing equipment. TMEIC's research has demonstrated that PID controllers provide excellent performance in steady-state operations but can struggle with complex transient responses[3]. Their LQR implementations address these limitations by incorporating full state feedback and optimizing multiple control objectives simultaneously. TMEIC has particularly focused on developing adaptive control systems that can automatically select between PID and LQR algorithms based on operating conditions, system identification results, and performance requirements[4]. This hybrid approach allows their industrial systems to maintain stability across varying loads while optimizing energy consumption and positioning accuracy.
Strengths: Extensive industrial implementation experience; robust solutions tested in demanding manufacturing environments; strong integration with existing industrial control systems. Weaknesses: Proprietary solutions may lack interoperability with third-party systems; higher implementation costs compared to standard PID-only solutions.
Weichai Power
Technical Solution: Weichai Power has developed advanced engine control systems that utilize both PID and LQR control methodologies to optimize performance across diverse operating conditions. Their diesel and natural gas engine management systems employ cascaded PID controllers for basic functions like idle speed control and fuel injection timing, providing reliable performance with minimal computational overhead[5]. For more complex challenges such as emissions control and transient response optimization, Weichai has implemented LQR-based controllers that consider multiple system states simultaneously. Their research demonstrates that while PID controllers offer simplicity and robustness for single-input-single-output subsystems, LQR provides superior performance for managing the complex interactions between air handling, fuel delivery, and exhaust aftertreatment systems[6]. Weichai's hybrid approach allows their engines to meet stringent emissions regulations while maintaining optimal fuel efficiency across varying loads and environmental conditions. Their control systems incorporate real-time adaptation mechanisms that adjust controller parameters based on operating conditions and component aging.
Strengths: Practical implementation in high-volume production engines; robust solutions tested across diverse operating environments; strong integration with mechanical systems. Weaknesses: Higher computational requirements for LQR implementation in real-time systems; increased complexity in calibration and maintenance procedures.
Key Algorithms and Mathematical Foundations
Special-shaped active vibration isolation platform adaptive to cabin arc surface and LQR control method thereof
PatentPendingCN119712772A
Innovation
- A special-shaped active vibration isolation platform adapted to the arc surface of the cabin was designed. Combined with the LQR control method, the acceleration information is measured in real time through a single-axis acceleration sensor, and closed-loop feedback control is adopted to realize active and passive hybrid vibration isolation, effectively suppressing high and low frequency vibration.
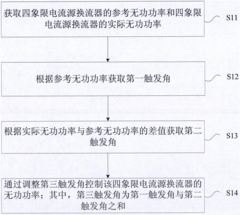
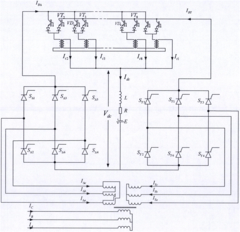
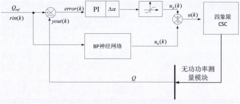
Reactive power control method and device of four-quadrant current source converter
PatentActiveCN106130030A
Innovation
- By obtaining the reference reactive power and actual reactive power of the four-quadrant current source converter, a composite method of neural network and PID controller is used to adjust the firing angle to control the reactive power. The specific steps include inputting the reference reactive power into the neural network. Obtain the first firing angle, obtain the second firing angle through the difference between the actual reactive power and the reference reactive power, and add the two to adjust the reactive power.
Computational Requirements and Performance Analysis
The computational requirements for PID and LQR control systems differ significantly, impacting their implementation feasibility across various applications. PID controllers demonstrate remarkable computational efficiency, typically requiring minimal processing power to calculate three simple terms (proportional, integral, derivative) and sum them. This lightweight computational footprint enables PID implementation on basic microcontrollers and PLCs, making it the preferred choice for resource-constrained environments or applications requiring high sampling rates. Most industrial PID implementations can execute at frequencies exceeding 1 kHz on standard hardware without optimization challenges.
In contrast, LQR controllers demand substantially higher computational resources. The implementation requires matrix operations including multiplication and inversion, with complexity scaling quadratically or cubically with the number of state variables. For real-time applications with numerous states, this can become prohibitively expensive. Additionally, LQR typically requires a complete state observer when not all states are directly measurable, further increasing computational overhead. These requirements often necessitate more powerful processors or dedicated hardware accelerators, particularly in complex systems.
Performance analysis reveals that PID controllers generally exhibit lower latency in response generation, which proves critical in time-sensitive applications like high-speed motion control. However, this computational simplicity comes with performance limitations in multivariable systems where cross-coupling effects become significant. LQR, despite its higher computational cost, delivers superior performance in such complex scenarios by explicitly accounting for interactions between system variables.
Memory requirements also differ substantially between these approaches. PID controllers maintain minimal state information (typically just the error integral and previous error values), requiring only a few bytes of memory regardless of system complexity. LQR implementations, however, must store state matrices and gain matrices, with memory requirements growing quadratically with the number of states and inputs.
When considering implementation platforms, PID controllers can be deployed virtually anywhere, from 8-bit microcontrollers to advanced industrial computers. LQR implementations typically require at minimum 32-bit processors with floating-point capabilities for reasonable performance, limiting deployment options in resource-constrained environments. This distinction becomes particularly relevant in embedded systems where power consumption, cost, and space constraints may dictate controller selection regardless of theoretical performance advantages.
In contrast, LQR controllers demand substantially higher computational resources. The implementation requires matrix operations including multiplication and inversion, with complexity scaling quadratically or cubically with the number of state variables. For real-time applications with numerous states, this can become prohibitively expensive. Additionally, LQR typically requires a complete state observer when not all states are directly measurable, further increasing computational overhead. These requirements often necessitate more powerful processors or dedicated hardware accelerators, particularly in complex systems.
Performance analysis reveals that PID controllers generally exhibit lower latency in response generation, which proves critical in time-sensitive applications like high-speed motion control. However, this computational simplicity comes with performance limitations in multivariable systems where cross-coupling effects become significant. LQR, despite its higher computational cost, delivers superior performance in such complex scenarios by explicitly accounting for interactions between system variables.
Memory requirements also differ substantially between these approaches. PID controllers maintain minimal state information (typically just the error integral and previous error values), requiring only a few bytes of memory regardless of system complexity. LQR implementations, however, must store state matrices and gain matrices, with memory requirements growing quadratically with the number of states and inputs.
When considering implementation platforms, PID controllers can be deployed virtually anywhere, from 8-bit microcontrollers to advanced industrial computers. LQR implementations typically require at minimum 32-bit processors with floating-point capabilities for reasonable performance, limiting deployment options in resource-constrained environments. This distinction becomes particularly relevant in embedded systems where power consumption, cost, and space constraints may dictate controller selection regardless of theoretical performance advantages.
Robustness and Stability Considerations
Robustness and stability represent critical considerations when comparing PID control systems with Linear Quadratic Regulator (LQR) approaches. PID controllers demonstrate remarkable robustness against model uncertainties and parameter variations, making them particularly valuable in industrial applications where precise system modeling may be challenging. This inherent robustness stems from their feedback-driven architecture, which continuously adjusts control signals based on real-time error measurements rather than relying heavily on accurate system models.
In contrast, LQR controllers exhibit higher sensitivity to modeling inaccuracies, as they fundamentally depend on precise state-space representations of the controlled system. When the actual system deviates from the mathematical model used for controller design, LQR performance may degrade significantly. This represents a substantial limitation in practical implementations where perfect modeling is rarely achievable.
Regarding stability margins, PID controllers offer well-established methods for stability analysis through classical control techniques such as Nyquist plots and Bode diagrams. Engineers can directly assess gain and phase margins, providing clear indicators of how much parameter variation the system can tolerate before becoming unstable. These quantifiable stability metrics facilitate straightforward controller tuning and validation.
LQR controllers, while mathematically guaranteed to be stable under ideal conditions, may exhibit reduced stability margins when confronted with real-world uncertainties. The optimal nature of LQR design prioritizes performance metrics defined by cost functions rather than explicitly addressing stability margins. Consequently, an LQR controller optimized for performance might operate closer to stability boundaries than a conservatively tuned PID controller.
Disturbance rejection capabilities differ significantly between these approaches. PID controllers can effectively handle external disturbances through integral action, though potentially at the cost of increased overshoot or settling time. LQR controllers can be designed with explicit disturbance models incorporated into the state-space representation, potentially achieving superior disturbance rejection for known disturbance characteristics.
For systems with time delays, PID controllers often demonstrate greater resilience, particularly when augmented with Smith predictors or other delay compensation techniques. LQR implementations typically struggle with time delays unless these are explicitly incorporated into the system model, which increases complexity and computational requirements.
The robustness-performance tradeoff emerges as a fundamental consideration: PID controllers generally prioritize robustness at some expense to optimal performance, while LQR approaches emphasize performance optimization potentially at the cost of reduced robustness against modeling uncertainties and parameter variations.
In contrast, LQR controllers exhibit higher sensitivity to modeling inaccuracies, as they fundamentally depend on precise state-space representations of the controlled system. When the actual system deviates from the mathematical model used for controller design, LQR performance may degrade significantly. This represents a substantial limitation in practical implementations where perfect modeling is rarely achievable.
Regarding stability margins, PID controllers offer well-established methods for stability analysis through classical control techniques such as Nyquist plots and Bode diagrams. Engineers can directly assess gain and phase margins, providing clear indicators of how much parameter variation the system can tolerate before becoming unstable. These quantifiable stability metrics facilitate straightforward controller tuning and validation.
LQR controllers, while mathematically guaranteed to be stable under ideal conditions, may exhibit reduced stability margins when confronted with real-world uncertainties. The optimal nature of LQR design prioritizes performance metrics defined by cost functions rather than explicitly addressing stability margins. Consequently, an LQR controller optimized for performance might operate closer to stability boundaries than a conservatively tuned PID controller.
Disturbance rejection capabilities differ significantly between these approaches. PID controllers can effectively handle external disturbances through integral action, though potentially at the cost of increased overshoot or settling time. LQR controllers can be designed with explicit disturbance models incorporated into the state-space representation, potentially achieving superior disturbance rejection for known disturbance characteristics.
For systems with time delays, PID controllers often demonstrate greater resilience, particularly when augmented with Smith predictors or other delay compensation techniques. LQR implementations typically struggle with time delays unless these are explicitly incorporated into the system model, which increases complexity and computational requirements.
The robustness-performance tradeoff emerges as a fundamental consideration: PID controllers generally prioritize robustness at some expense to optimal performance, while LQR approaches emphasize performance optimization potentially at the cost of reduced robustness against modeling uncertainties and parameter variations.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!