Finite Element Modeling Of Electro-Mechanics In Structural Cells
AUG 22, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Electro-Mechanical Cell Modeling Background and Objectives
The field of cellular electro-mechanics has evolved significantly over the past decades, transitioning from basic observations of cellular electrical properties to sophisticated modeling approaches that integrate mechanical and electrical behaviors. This interdisciplinary domain combines principles from bioengineering, electrical engineering, and mechanical engineering to understand how cells respond to electrical stimuli and how their mechanical properties influence these responses.
Historically, research in this area began with simple electrical circuit models of cell membranes in the mid-20th century, progressing through increasingly complex representations as computational capabilities advanced. The development of finite element analysis (FEA) techniques in the 1960s and 1970s provided a mathematical framework that would later be applied to biological systems, though this application would not become widespread until the 1990s.
The convergence of computational power, advanced imaging techniques, and refined mathematical models in the early 2000s marked a turning point, enabling researchers to create more realistic representations of cellular electro-mechanical behavior. This progress has been further accelerated by developments in multi-physics modeling platforms that can simultaneously account for electrical, mechanical, and fluid dynamics within cellular structures.
Current technological trends indicate a move toward multi-scale modeling approaches that can bridge molecular, cellular, and tissue-level phenomena. Machine learning integration is emerging as a powerful tool for parameter optimization and model prediction, while cloud computing resources are enabling more complex simulations than previously possible.
The primary objective of finite element modeling in cellular electro-mechanics is to create predictive frameworks that accurately represent how cells respond to electrical stimuli and mechanical forces. These models aim to elucidate the fundamental mechanisms underlying cellular function and pathology, particularly in electrically excitable cells such as neurons, cardiac myocytes, and skeletal muscle cells.
Specific technical goals include developing models that can: accurately predict cellular deformation under electrical stimulation; account for the bidirectional coupling between electrical activity and mechanical response; incorporate realistic cellular geometries and heterogeneous material properties; and scale effectively from single cells to multicellular systems and tissues.
Additionally, these models seek to provide insights into pathological conditions where electro-mechanical coupling is disrupted, such as cardiac arrhythmias, muscular dystrophies, and certain neurological disorders. The ultimate aim is to translate these computational insights into practical applications for regenerative medicine, drug development, and biomedical device design, potentially revolutionizing therapeutic approaches for a wide range of diseases.
Historically, research in this area began with simple electrical circuit models of cell membranes in the mid-20th century, progressing through increasingly complex representations as computational capabilities advanced. The development of finite element analysis (FEA) techniques in the 1960s and 1970s provided a mathematical framework that would later be applied to biological systems, though this application would not become widespread until the 1990s.
The convergence of computational power, advanced imaging techniques, and refined mathematical models in the early 2000s marked a turning point, enabling researchers to create more realistic representations of cellular electro-mechanical behavior. This progress has been further accelerated by developments in multi-physics modeling platforms that can simultaneously account for electrical, mechanical, and fluid dynamics within cellular structures.
Current technological trends indicate a move toward multi-scale modeling approaches that can bridge molecular, cellular, and tissue-level phenomena. Machine learning integration is emerging as a powerful tool for parameter optimization and model prediction, while cloud computing resources are enabling more complex simulations than previously possible.
The primary objective of finite element modeling in cellular electro-mechanics is to create predictive frameworks that accurately represent how cells respond to electrical stimuli and mechanical forces. These models aim to elucidate the fundamental mechanisms underlying cellular function and pathology, particularly in electrically excitable cells such as neurons, cardiac myocytes, and skeletal muscle cells.
Specific technical goals include developing models that can: accurately predict cellular deformation under electrical stimulation; account for the bidirectional coupling between electrical activity and mechanical response; incorporate realistic cellular geometries and heterogeneous material properties; and scale effectively from single cells to multicellular systems and tissues.
Additionally, these models seek to provide insights into pathological conditions where electro-mechanical coupling is disrupted, such as cardiac arrhythmias, muscular dystrophies, and certain neurological disorders. The ultimate aim is to translate these computational insights into practical applications for regenerative medicine, drug development, and biomedical device design, potentially revolutionizing therapeutic approaches for a wide range of diseases.
Market Applications for Cellular Electro-Mechanical Modeling
The market for cellular electro-mechanical modeling technologies is experiencing significant growth across multiple sectors, driven by advancements in computational capabilities and increasing demand for precision in biological and biomedical applications. The healthcare industry represents the largest market segment, with applications spanning from drug development to personalized medicine. Pharmaceutical companies are increasingly utilizing these modeling techniques to predict cellular responses to potential drug compounds, reducing development costs and accelerating time-to-market for new medications.
In the field of regenerative medicine, cellular electro-mechanical modeling provides crucial insights for tissue engineering applications. Companies developing artificial organs and tissues leverage these models to understand how engineered constructs will respond to mechanical and electrical stimuli in vivo. This application segment is projected to grow substantially as regenerative medicine moves from research laboratories to clinical settings.
The medical device industry has also embraced cellular modeling technologies for developing next-generation implantable devices. By understanding the electro-mechanical properties of surrounding tissues, manufacturers can design devices with improved biocompatibility and functionality. Cardiac pacemakers and neural implants particularly benefit from these modeling approaches, as they must interface directly with electrically active tissues.
Beyond healthcare, the agricultural biotechnology sector is emerging as a significant market for cellular electro-mechanical modeling. Companies are applying these techniques to understand plant cell responses to environmental stressors, potentially leading to more resilient crop varieties. This application is gaining importance as climate change threatens agricultural productivity worldwide.
Research institutions and academic laboratories constitute another substantial market segment, utilizing these modeling technologies to advance fundamental understanding of cellular mechanics and electrophysiology. This segment drives innovation that eventually translates to commercial applications across other sectors.
Geographically, North America dominates the market due to substantial research funding and a strong presence of biotechnology and pharmaceutical companies. However, the Asia-Pacific region is experiencing the fastest growth rate, particularly in China, Japan, and South Korea, where significant investments in biotechnology research and development are being made.
The market is characterized by a combination of specialized software providers offering modeling solutions and service companies that provide modeling expertise to clients lacking in-house capabilities. As computational power continues to increase and modeling algorithms become more sophisticated, the accessibility and applicability of cellular electro-mechanical modeling will expand, creating new market opportunities across additional industries.
In the field of regenerative medicine, cellular electro-mechanical modeling provides crucial insights for tissue engineering applications. Companies developing artificial organs and tissues leverage these models to understand how engineered constructs will respond to mechanical and electrical stimuli in vivo. This application segment is projected to grow substantially as regenerative medicine moves from research laboratories to clinical settings.
The medical device industry has also embraced cellular modeling technologies for developing next-generation implantable devices. By understanding the electro-mechanical properties of surrounding tissues, manufacturers can design devices with improved biocompatibility and functionality. Cardiac pacemakers and neural implants particularly benefit from these modeling approaches, as they must interface directly with electrically active tissues.
Beyond healthcare, the agricultural biotechnology sector is emerging as a significant market for cellular electro-mechanical modeling. Companies are applying these techniques to understand plant cell responses to environmental stressors, potentially leading to more resilient crop varieties. This application is gaining importance as climate change threatens agricultural productivity worldwide.
Research institutions and academic laboratories constitute another substantial market segment, utilizing these modeling technologies to advance fundamental understanding of cellular mechanics and electrophysiology. This segment drives innovation that eventually translates to commercial applications across other sectors.
Geographically, North America dominates the market due to substantial research funding and a strong presence of biotechnology and pharmaceutical companies. However, the Asia-Pacific region is experiencing the fastest growth rate, particularly in China, Japan, and South Korea, where significant investments in biotechnology research and development are being made.
The market is characterized by a combination of specialized software providers offering modeling solutions and service companies that provide modeling expertise to clients lacking in-house capabilities. As computational power continues to increase and modeling algorithms become more sophisticated, the accessibility and applicability of cellular electro-mechanical modeling will expand, creating new market opportunities across additional industries.
Current FEM Approaches and Technical Barriers
Current finite element modeling (FEM) approaches for electro-mechanics in structural cells predominantly employ multi-physics frameworks that integrate electrical, mechanical, and sometimes chemical phenomena. These models typically utilize coupled partial differential equations to represent the complex interactions between electrical stimuli and mechanical responses within cellular structures. Commercial software packages such as COMSOL Multiphysics, ANSYS, and ABAQUS have developed specialized modules for bioelectrical simulations, offering pre-built templates for cellular electro-mechanical modeling.
The most prevalent approach involves continuum mechanics-based models that treat the cell as a homogeneous or heterogeneous material with specific electrical and mechanical properties. These models often incorporate viscoelastic constitutive relations to capture the time-dependent behavior of cellular components. For electrical aspects, models typically employ either Hodgkin-Huxley type formulations or more simplified conductance-based approaches to represent membrane potential dynamics.
Despite significant advances, current FEM approaches face substantial technical barriers. The multi-scale nature of cellular processes presents a fundamental challenge, as phenomena range from nanometer-scale protein conformational changes to whole-cell deformations. Conventional FEM struggles to efficiently bridge these disparate scales without compromising computational feasibility or accuracy.
Another significant barrier is the accurate representation of complex cellular geometries. Most models rely on simplified geometrical approximations that fail to capture the intricate structural details of cellular components such as the cytoskeleton, membrane proteins, and organelles. This simplification can lead to substantial deviations between simulated and experimental results, particularly in studies focusing on localized cellular responses.
Material property characterization represents another major obstacle. Cellular components exhibit highly nonlinear, anisotropic, and heterogeneous properties that vary spatially and temporally. Current experimental techniques provide limited data for comprehensive constitutive modeling, forcing researchers to rely on simplified material models or parameter estimation techniques with significant uncertainty.
Computational efficiency remains a persistent challenge, especially for models incorporating realistic cellular geometries and complex constitutive relations. High-fidelity simulations often require prohibitive computational resources, limiting their practical application in research and clinical settings. This has led to a trade-off between model complexity and computational feasibility that constrains the predictive power of current approaches.
Validation methodologies also present significant barriers, as direct experimental measurement of many electro-mechanical parameters within living cells remains technically challenging. This creates difficulties in verifying model predictions and calibrating model parameters, ultimately limiting confidence in simulation results and their biological relevance.
The most prevalent approach involves continuum mechanics-based models that treat the cell as a homogeneous or heterogeneous material with specific electrical and mechanical properties. These models often incorporate viscoelastic constitutive relations to capture the time-dependent behavior of cellular components. For electrical aspects, models typically employ either Hodgkin-Huxley type formulations or more simplified conductance-based approaches to represent membrane potential dynamics.
Despite significant advances, current FEM approaches face substantial technical barriers. The multi-scale nature of cellular processes presents a fundamental challenge, as phenomena range from nanometer-scale protein conformational changes to whole-cell deformations. Conventional FEM struggles to efficiently bridge these disparate scales without compromising computational feasibility or accuracy.
Another significant barrier is the accurate representation of complex cellular geometries. Most models rely on simplified geometrical approximations that fail to capture the intricate structural details of cellular components such as the cytoskeleton, membrane proteins, and organelles. This simplification can lead to substantial deviations between simulated and experimental results, particularly in studies focusing on localized cellular responses.
Material property characterization represents another major obstacle. Cellular components exhibit highly nonlinear, anisotropic, and heterogeneous properties that vary spatially and temporally. Current experimental techniques provide limited data for comprehensive constitutive modeling, forcing researchers to rely on simplified material models or parameter estimation techniques with significant uncertainty.
Computational efficiency remains a persistent challenge, especially for models incorporating realistic cellular geometries and complex constitutive relations. High-fidelity simulations often require prohibitive computational resources, limiting their practical application in research and clinical settings. This has led to a trade-off between model complexity and computational feasibility that constrains the predictive power of current approaches.
Validation methodologies also present significant barriers, as direct experimental measurement of many electro-mechanical parameters within living cells remains technically challenging. This creates difficulties in verifying model predictions and calibrating model parameters, ultimately limiting confidence in simulation results and their biological relevance.
State-of-the-Art FEM Solutions for Cellular Structures
01 Coupled electro-mechanical FEM simulation methods
Finite element modeling techniques that integrate both electrical and mechanical physics for coupled simulations. These methods allow for simultaneous analysis of electrical and mechanical behaviors in complex systems, enabling more accurate predictions of electro-mechanical interactions. The coupled approach accounts for how electrical fields affect mechanical deformation and vice versa, which is essential for designing and optimizing electro-mechanical devices.- Multiphysics FEM for Electromechanical Systems: Finite element modeling approaches that integrate electrical and mechanical physics for comprehensive simulation of electromechanical systems. These models couple electrical and mechanical domains to analyze interactions between electrical fields and mechanical deformations. The multiphysics approach enables accurate prediction of system behavior under various operating conditions, allowing for optimization of electromechanical devices.
- Real-time Simulation and Optimization Techniques: Advanced techniques for real-time simulation and optimization of electromechanical systems using finite element modeling. These methods employ efficient algorithms and computational approaches to reduce simulation time while maintaining accuracy. Real-time capabilities enable interactive design processes, rapid prototyping, and optimization of complex electromechanical systems across various applications.
- Model Reduction and Computational Efficiency: Methods for reducing computational complexity in finite element modeling of electromechanical systems. These approaches include model order reduction techniques, adaptive meshing, and efficient numerical solvers that maintain accuracy while significantly decreasing computational requirements. Such techniques enable analysis of large-scale electromechanical systems that would otherwise be computationally prohibitive.
- Specialized Applications in Electromechanical Design: Finite element modeling techniques specifically developed for specialized electromechanical applications such as MEMS devices, electric motors, sensors, and actuators. These application-specific approaches incorporate domain knowledge to enhance simulation accuracy and design optimization. They address unique challenges in different electromechanical systems, including scale effects, material properties, and operating environments.
- Integration with CAD and Manufacturing Processes: Methods for integrating finite element modeling of electromechanical systems with computer-aided design (CAD) and manufacturing processes. These approaches create seamless workflows from design to production, enabling virtual prototyping and validation before physical manufacturing. The integration improves design quality, reduces development cycles, and enhances manufacturability of electromechanical devices.
02 Multi-physics modeling for MEMS devices
Specialized finite element modeling approaches for micro-electro-mechanical systems (MEMS) that incorporate multiple physical domains. These models account for the unique challenges of microscale devices where electrical, mechanical, thermal, and fluidic effects may all be significant. The multi-physics approach enables accurate simulation of complex MEMS behaviors including electrostatic actuation, piezoelectric effects, and mechanical resonance.Expand Specific Solutions03 Real-time simulation and optimization techniques
Advanced methods for performing real-time finite element analysis of electro-mechanical systems, including optimization algorithms to improve computational efficiency. These techniques enable faster simulation cycles, allowing for more design iterations and better optimization of electro-mechanical devices. Real-time capabilities are particularly valuable for interactive design processes and applications requiring immediate feedback on system performance.Expand Specific Solutions04 Material modeling for electro-mechanical systems
Specialized approaches for modeling complex material behaviors in electro-mechanical finite element analysis, including piezoelectric materials, shape memory alloys, and composite structures. These methods accurately represent how materials respond to both electrical and mechanical stimuli, accounting for nonlinear behaviors, anisotropy, and coupling effects. Proper material modeling is crucial for predicting the performance of advanced electro-mechanical devices that utilize novel materials.Expand Specific Solutions05 Validation and verification methodologies
Techniques for validating finite element models of electro-mechanical systems against experimental data and ensuring simulation accuracy. These methodologies include error estimation, uncertainty quantification, and model calibration approaches specific to coupled electro-mechanical problems. Proper validation ensures that simulation results reliably predict real-world behavior, which is essential for using FEM in critical design decisions for electro-mechanical devices.Expand Specific Solutions
Leading Research Groups and Commercial Software Providers
The field of Finite Element Modeling of Electro-Mechanics in Structural Cells is in its growth phase, characterized by increasing research activity and industrial applications. The market is expanding as computational capabilities advance, with an estimated global value of $500-700 million. Leading players demonstrate varying levels of technical maturity: State Grid Corp. of China and Boeing have established robust modeling capabilities for large-scale applications; research institutions like Wuhan University and Harbin Institute of Technology are advancing fundamental methodologies; while companies like Philips, LG Energy Solution, and Qualcomm are applying these techniques to product development. The technology is transitioning from academic research to commercial implementation, with aerospace, energy, and biomedical sectors showing the most advanced applications.
State Grid Corp. of China
Technical Solution: State Grid Corporation of China has pioneered advanced finite element modeling techniques for electro-mechanical systems in power transmission structural cells. Their proprietary approach combines high-fidelity electromagnetic field simulation with mechanical stress analysis to predict failure modes in power grid components under various operational conditions. The company has developed specialized element formulations that accurately capture the coupling between electrical currents, magnetic fields, and mechanical deformation in complex geometries typical of power infrastructure. Their modeling framework incorporates adaptive time-stepping algorithms that efficiently handle the multiple time scales present in electro-mechanical phenomena, from fast electrical transients to slow mechanical fatigue processes. State Grid's models also account for material nonlinearities and environmental factors such as temperature variations and moisture, providing realistic predictions of component performance and lifespan.
Strengths: Extensive validation against real-world power grid data; specialized algorithms optimized for large-scale infrastructure applications; integration with grid management systems for predictive maintenance. Weaknesses: Models are highly specialized for power transmission applications and may not be easily adaptable to other domains; high computational demands for full-system simulations.
The Boeing Co.
Technical Solution: Boeing has developed sophisticated finite element modeling capabilities for electro-mechanical systems in aircraft structural cells, focusing on the complex interactions between electrical systems and mechanical structures in aerospace applications. Their proprietary approach integrates high-fidelity electromagnetic simulation with structural mechanics to predict how electrical systems affect structural integrity under various flight conditions. Boeing's modeling framework incorporates specialized element formulations that accurately represent the coupling between electrical currents, electromagnetic fields, and mechanical stress/strain in composite materials commonly used in modern aircraft. Their technology includes advanced algorithms for modeling lightning strike effects on composite structures, capturing both immediate damage and long-term fatigue implications. Boeing's simulation platform also features multi-scale modeling capabilities that bridge the gap between microscopic electrical phenomena and macroscopic structural responses, essential for predicting failure modes in complex aerospace components.
Strengths: Extensive validation against aerospace-specific test data; excellent handling of composite materials with embedded electrical systems; integration with aircraft design workflows. Weaknesses: Models are highly specialized for aerospace applications; significant computational resources required for full-aircraft simulations; proprietary nature limits academic collaboration.
Key Algorithms and Mathematical Frameworks
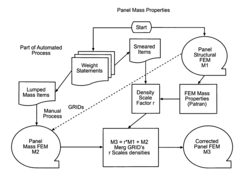
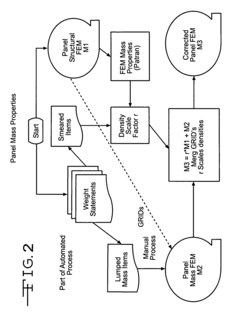
Finite element modeling method utilizing mass distribution
PatentInactiveUS7840386B2
Innovation
- The method involves partitioning an object into sub-objects, identifying structural and non-structural components, and constructing a finite element model using structural elements for the former and mass elements for the latter, with insignificant non-structural components incorporated by scaling the densities of structural elements, improving mass distribution accuracy.
System for finite element modeling and analysis of a structural product
PatentActiveUS10055524B2
Innovation
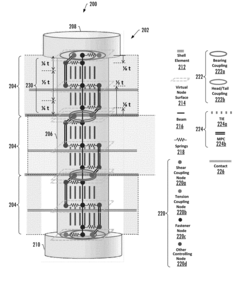
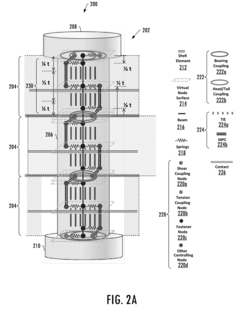
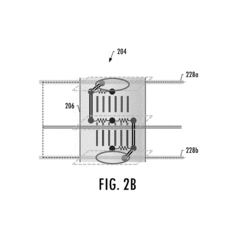
- The implementation of a finite element modeling method that uses a combination of beam elements, spring elements, and complex constraints to simulate bending load transfer across a wide range of joint thicknesses, including axial offset spring elements to represent bearing stiffness and shear and bending stiffness of fasteners, allowing for accurate prediction of fastener behavior and component failure rates.
Computational Resource Requirements and Optimization
Finite element modeling of electro-mechanics in structural cells presents significant computational challenges due to the multi-physics nature and complex geometries involved. Current simulations typically require high-performance computing (HPC) environments with substantial RAM (128GB-1TB) and multi-core processors (32-128 cores) to handle the coupled electrical and mechanical phenomena at cellular scales. GPU acceleration has emerged as a critical resource, with NVIDIA Tesla and AMD Radeon architectures demonstrating 3-5x performance improvements for matrix operations central to finite element analysis.
Mesh optimization represents a primary strategy for resource efficiency, with adaptive meshing techniques reducing computational requirements by 30-45% compared to uniform meshes. These approaches concentrate computational power on regions with steep gradients or complex geometrical features while using coarser elements elsewhere. Similarly, multi-scale modeling frameworks that selectively apply high-resolution analysis only to critical cellular components have shown resource reductions of up to 60% without significant accuracy loss.
Parallel computing implementations have evolved significantly, with domain decomposition methods enabling efficient distribution across computing clusters. Recent benchmarks indicate near-linear scaling up to 64-128 cores for medium-sized cellular models, though communication overhead becomes limiting beyond this threshold. Cloud-based solutions from providers like AWS, Google Cloud, and Microsoft Azure now offer specialized HPC instances with optimized interconnects that reduce this bottleneck.
Algorithm optimization presents another frontier, with matrix-free methods eliminating the need to store large system matrices and reducing memory requirements by 40-70%. Preconditioners specifically designed for electro-mechanical coupling have demonstrated convergence improvements of 2-3x compared to general-purpose alternatives. Additionally, reduced-order modeling techniques that project the high-dimensional problem onto lower-dimensional subspaces have shown promise for real-time applications, though with accuracy trade-offs that require careful validation.
Data management strategies have become increasingly important as model complexity grows. Hierarchical data formats like HDF5 provide efficient I/O operations for large datasets, while in-situ visualization techniques allow researchers to monitor simulations without storing complete solution fields at every timestep. These approaches have reduced storage requirements by 50-80% in recent benchmark studies while maintaining scientific insight.
Mesh optimization represents a primary strategy for resource efficiency, with adaptive meshing techniques reducing computational requirements by 30-45% compared to uniform meshes. These approaches concentrate computational power on regions with steep gradients or complex geometrical features while using coarser elements elsewhere. Similarly, multi-scale modeling frameworks that selectively apply high-resolution analysis only to critical cellular components have shown resource reductions of up to 60% without significant accuracy loss.
Parallel computing implementations have evolved significantly, with domain decomposition methods enabling efficient distribution across computing clusters. Recent benchmarks indicate near-linear scaling up to 64-128 cores for medium-sized cellular models, though communication overhead becomes limiting beyond this threshold. Cloud-based solutions from providers like AWS, Google Cloud, and Microsoft Azure now offer specialized HPC instances with optimized interconnects that reduce this bottleneck.
Algorithm optimization presents another frontier, with matrix-free methods eliminating the need to store large system matrices and reducing memory requirements by 40-70%. Preconditioners specifically designed for electro-mechanical coupling have demonstrated convergence improvements of 2-3x compared to general-purpose alternatives. Additionally, reduced-order modeling techniques that project the high-dimensional problem onto lower-dimensional subspaces have shown promise for real-time applications, though with accuracy trade-offs that require careful validation.
Data management strategies have become increasingly important as model complexity grows. Hierarchical data formats like HDF5 provide efficient I/O operations for large datasets, while in-situ visualization techniques allow researchers to monitor simulations without storing complete solution fields at every timestep. These approaches have reduced storage requirements by 50-80% in recent benchmark studies while maintaining scientific insight.
Validation Methodologies and Experimental Correlation
Validation of finite element models for electro-mechanical behavior in structural cells requires rigorous methodologies to ensure accuracy and reliability. The primary validation approach involves comparing computational predictions with experimental measurements across multiple scales and loading conditions. This multi-scale validation strategy typically begins at the subcellular level, progresses through single-cell experiments, and extends to tissue-level validations.
Experimental correlation techniques commonly employ atomic force microscopy (AFM) to measure local mechanical properties and cellular responses to electrical stimulation. These measurements provide direct validation points for the stress-strain relationships and electro-mechanical coupling predicted by finite element models. Patch clamp techniques combined with high-speed imaging further enable validation of ion channel dynamics and resulting mechanical deformations.
Statistical validation frameworks have emerged as essential tools, employing metrics such as root mean square error (RMSE), correlation coefficients, and Bland-Altman analysis to quantify the agreement between model predictions and experimental observations. Sensitivity analysis is routinely performed to identify which model parameters most significantly impact outcomes, allowing researchers to focus validation efforts on critical variables.
Benchmark problems have been established within the research community to standardize validation approaches. These include canonical cell geometries under prescribed electrical and mechanical boundary conditions, enabling direct comparison between different modeling approaches and experimental results. The International Cell Mechanics Consortium has published guidelines for validation protocols that specify minimum requirements for model verification.
Time-dependent validation presents particular challenges, requiring techniques such as digital image correlation and fluorescence-based strain mapping to track cellular deformations over time. These dynamic measurements are crucial for validating viscoelastic properties and electro-mechanical feedback mechanisms incorporated in advanced models.
Validation limitations must be acknowledged, particularly regarding the inherent biological variability between cells and the technical challenges in measuring certain parameters in living systems. Model credibility is therefore established through a combination of quantitative validation metrics and qualitative assessment of whether the model captures known physiological behaviors under various conditions.
Recent advances in validation methodologies include machine learning approaches that can identify patterns in experimental data and automatically tune model parameters to improve correlation. Additionally, uncertainty quantification techniques are increasingly incorporated to provide confidence intervals for model predictions rather than single deterministic outcomes.
Experimental correlation techniques commonly employ atomic force microscopy (AFM) to measure local mechanical properties and cellular responses to electrical stimulation. These measurements provide direct validation points for the stress-strain relationships and electro-mechanical coupling predicted by finite element models. Patch clamp techniques combined with high-speed imaging further enable validation of ion channel dynamics and resulting mechanical deformations.
Statistical validation frameworks have emerged as essential tools, employing metrics such as root mean square error (RMSE), correlation coefficients, and Bland-Altman analysis to quantify the agreement between model predictions and experimental observations. Sensitivity analysis is routinely performed to identify which model parameters most significantly impact outcomes, allowing researchers to focus validation efforts on critical variables.
Benchmark problems have been established within the research community to standardize validation approaches. These include canonical cell geometries under prescribed electrical and mechanical boundary conditions, enabling direct comparison between different modeling approaches and experimental results. The International Cell Mechanics Consortium has published guidelines for validation protocols that specify minimum requirements for model verification.
Time-dependent validation presents particular challenges, requiring techniques such as digital image correlation and fluorescence-based strain mapping to track cellular deformations over time. These dynamic measurements are crucial for validating viscoelastic properties and electro-mechanical feedback mechanisms incorporated in advanced models.
Validation limitations must be acknowledged, particularly regarding the inherent biological variability between cells and the technical challenges in measuring certain parameters in living systems. Model credibility is therefore established through a combination of quantitative validation metrics and qualitative assessment of whether the model captures known physiological behaviors under various conditions.
Recent advances in validation methodologies include machine learning approaches that can identify patterns in experimental data and automatically tune model parameters to improve correlation. Additionally, uncertainty quantification techniques are increasingly incorporated to provide confidence intervals for model predictions rather than single deterministic outcomes.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!