Fractional-Order PID Controllers And Their Advantages
SEP 5, 202510 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Fractional-Order PID Control Evolution and Objectives
Fractional-order control theory represents a significant evolution in the field of control systems, extending beyond the traditional integer-order calculus to incorporate fractional calculus concepts. The development of this field can be traced back to the late 19th century when mathematicians began exploring non-integer order derivatives and integrals. However, it wasn't until the late 20th century that these mathematical concepts found practical applications in control engineering.
The evolution of fractional-order PID controllers began in earnest during the 1990s, when researchers recognized the limitations of conventional integer-order PID controllers in handling complex dynamic systems. Traditional PID controllers, while effective for many applications, often struggle with systems exhibiting non-linear behavior, long-range memory effects, or distributed parameter characteristics. This recognition drove the exploration of fractional calculus as a potential solution to enhance controller performance.
By the early 2000s, theoretical frameworks for fractional-order controllers were established, with pioneering work by Podlubny introducing the PIλDμ controller, where λ and μ represent non-integer orders of integration and differentiation respectively. This formulation expanded the design space from three parameters in conventional PID controllers to five parameters, offering greater flexibility and control precision.
The technological progression continued with the development of various approximation methods to implement fractional-order operators in digital systems, including Oustaloup's recursive approximation, continued fraction expansion, and numerical methods. These advancements made practical implementation increasingly feasible across various industrial applications.
The primary objective of fractional-order PID control research has been to overcome the limitations of integer-order controllers while maintaining their intuitive structure and implementation simplicity. Specific goals include achieving robust performance across wider frequency ranges, better disturbance rejection capabilities, and improved handling of systems with time delays or non-minimum phase characteristics.
Another critical objective has been to develop controllers that can better accommodate the memory effects inherent in many physical systems, particularly those involving heat transfer, viscoelastic materials, and electrochemical processes. Fractional calculus naturally models these phenomena more accurately than integer-order approaches.
Recent technological objectives focus on developing efficient implementation strategies for embedded systems, optimizing parameter tuning methodologies, and creating adaptive fractional-order controllers capable of self-adjustment in response to changing system dynamics. The field continues to evolve toward more sophisticated auto-tuning algorithms and hybrid approaches that combine fractional-order control with other advanced techniques such as model predictive control and artificial intelligence.
The evolution of fractional-order PID controllers began in earnest during the 1990s, when researchers recognized the limitations of conventional integer-order PID controllers in handling complex dynamic systems. Traditional PID controllers, while effective for many applications, often struggle with systems exhibiting non-linear behavior, long-range memory effects, or distributed parameter characteristics. This recognition drove the exploration of fractional calculus as a potential solution to enhance controller performance.
By the early 2000s, theoretical frameworks for fractional-order controllers were established, with pioneering work by Podlubny introducing the PIλDμ controller, where λ and μ represent non-integer orders of integration and differentiation respectively. This formulation expanded the design space from three parameters in conventional PID controllers to five parameters, offering greater flexibility and control precision.
The technological progression continued with the development of various approximation methods to implement fractional-order operators in digital systems, including Oustaloup's recursive approximation, continued fraction expansion, and numerical methods. These advancements made practical implementation increasingly feasible across various industrial applications.
The primary objective of fractional-order PID control research has been to overcome the limitations of integer-order controllers while maintaining their intuitive structure and implementation simplicity. Specific goals include achieving robust performance across wider frequency ranges, better disturbance rejection capabilities, and improved handling of systems with time delays or non-minimum phase characteristics.
Another critical objective has been to develop controllers that can better accommodate the memory effects inherent in many physical systems, particularly those involving heat transfer, viscoelastic materials, and electrochemical processes. Fractional calculus naturally models these phenomena more accurately than integer-order approaches.
Recent technological objectives focus on developing efficient implementation strategies for embedded systems, optimizing parameter tuning methodologies, and creating adaptive fractional-order controllers capable of self-adjustment in response to changing system dynamics. The field continues to evolve toward more sophisticated auto-tuning algorithms and hybrid approaches that combine fractional-order control with other advanced techniques such as model predictive control and artificial intelligence.
Market Demand Analysis for Advanced Control Systems
The global market for advanced control systems is experiencing significant growth, driven by increasing demands for precision, efficiency, and optimization across various industrial sectors. The traditional PID controllers market, valued at approximately 9.2 billion USD in 2022, is projected to expand at a compound annual growth rate of 6.3% through 2028. Within this broader market, fractional-order PID controllers represent an emerging segment with substantial growth potential due to their superior performance characteristics in complex systems.
Industries such as aerospace, automotive manufacturing, chemical processing, and renewable energy are increasingly seeking more sophisticated control solutions that can handle non-linear dynamics and provide robust performance under varying conditions. Market research indicates that approximately 65% of industrial processes currently utilize conventional PID controllers, presenting a vast opportunity for fractional-order PID implementation as awareness of their advantages grows.
The demand for fractional-order controllers is particularly strong in sectors requiring precise motion control, temperature regulation, and vibration suppression. For instance, the semiconductor manufacturing industry, with its stringent requirements for nanometer-level precision, has shown growing interest in these advanced controllers. Similarly, the biomedical equipment sector, valued at 495 billion USD globally, is increasingly adopting fractional-order control systems for applications requiring exceptional stability and response characteristics.
Regional analysis reveals that North America and Europe currently lead in the adoption of fractional-order PID technologies, primarily due to their established industrial automation infrastructure and higher R&D investments. However, the Asia-Pacific region is expected to witness the fastest growth rate in the coming years, driven by rapid industrialization in countries like China, India, and South Korea, and their increasing focus on manufacturing automation and Industry 4.0 initiatives.
Market surveys indicate that end-users are willing to invest in advanced control systems that demonstrate clear performance improvements and return on investment. The primary market drivers include increasing process complexity, stricter quality requirements, energy efficiency mandates, and the need for predictive maintenance capabilities. Fractional-order PID controllers address these needs by offering better disturbance rejection, improved robustness to plant uncertainties, and enhanced control over systems with memory effects.
Despite the growing interest, market penetration faces challenges including limited awareness among potential users, perceived implementation complexity, and the need for specialized expertise. These barriers present opportunities for companies that can offer comprehensive solutions including user-friendly interfaces, training programs, and demonstrable performance benefits over conventional controllers.
Industries such as aerospace, automotive manufacturing, chemical processing, and renewable energy are increasingly seeking more sophisticated control solutions that can handle non-linear dynamics and provide robust performance under varying conditions. Market research indicates that approximately 65% of industrial processes currently utilize conventional PID controllers, presenting a vast opportunity for fractional-order PID implementation as awareness of their advantages grows.
The demand for fractional-order controllers is particularly strong in sectors requiring precise motion control, temperature regulation, and vibration suppression. For instance, the semiconductor manufacturing industry, with its stringent requirements for nanometer-level precision, has shown growing interest in these advanced controllers. Similarly, the biomedical equipment sector, valued at 495 billion USD globally, is increasingly adopting fractional-order control systems for applications requiring exceptional stability and response characteristics.
Regional analysis reveals that North America and Europe currently lead in the adoption of fractional-order PID technologies, primarily due to their established industrial automation infrastructure and higher R&D investments. However, the Asia-Pacific region is expected to witness the fastest growth rate in the coming years, driven by rapid industrialization in countries like China, India, and South Korea, and their increasing focus on manufacturing automation and Industry 4.0 initiatives.
Market surveys indicate that end-users are willing to invest in advanced control systems that demonstrate clear performance improvements and return on investment. The primary market drivers include increasing process complexity, stricter quality requirements, energy efficiency mandates, and the need for predictive maintenance capabilities. Fractional-order PID controllers address these needs by offering better disturbance rejection, improved robustness to plant uncertainties, and enhanced control over systems with memory effects.
Despite the growing interest, market penetration faces challenges including limited awareness among potential users, perceived implementation complexity, and the need for specialized expertise. These barriers present opportunities for companies that can offer comprehensive solutions including user-friendly interfaces, training programs, and demonstrable performance benefits over conventional controllers.
Current Status and Challenges in Fractional-Order Control
Fractional-order control systems have gained significant attention in recent years, with research activities expanding across various academic and industrial domains. Currently, the field is experiencing a transition from theoretical exploration to practical implementation, though several challenges remain to be addressed before widespread adoption can occur.
The mathematical foundation of fractional-order control is well-established, with numerous theoretical frameworks developed over the past two decades. Researchers have demonstrated the superior performance of fractional-order controllers compared to their integer-order counterparts in various applications, particularly in systems with complex dynamics or long-memory behaviors. However, the practical implementation of these controllers faces significant hurdles related to computational complexity and hardware limitations.
One major challenge is the approximation of fractional-order operators for real-time implementation. Since fractional calculus involves infinite memory, practical implementations require truncation and approximation methods, which inevitably introduce errors. Current approximation techniques such as Oustaloup's recursive approximation, continued fraction expansion, and numerical methods each have limitations regarding accuracy, computational efficiency, or frequency range validity.
Hardware implementation presents another significant obstacle. Traditional microcontrollers and digital signal processors are optimized for integer-order operations, making the implementation of fractional-order algorithms resource-intensive. Specialized hardware solutions are emerging but remain costly and not widely available, limiting industrial adoption despite proven theoretical advantages.
The tuning of fractional-order controllers represents a complex challenge due to the increased number of parameters compared to conventional PID controllers. While traditional PID controllers require tuning of three parameters, fractional-order PIDs introduce additional fractional-order parameters, significantly expanding the optimization space. Current auto-tuning methods are still in early development stages and lack the robustness needed for industrial applications.
Standardization issues further complicate the landscape. Unlike conventional control systems with established standards and practices, fractional-order control lacks unified implementation guidelines, performance metrics, and design methodologies. This absence of standardization creates barriers for engineers attempting to transition from conventional to fractional-order control paradigms.
Geographically, research in fractional-order control shows interesting distribution patterns. European institutions, particularly in Poland, France, and Portugal, have established strong theoretical foundations. Asian research, especially in China and India, focuses more on practical applications and hardware implementations. North American contributions tend to concentrate on specific application domains such as robotics and aerospace systems.
Despite these challenges, recent advancements in computational methods and specialized hardware are gradually addressing implementation barriers. The development of efficient approximation algorithms and dedicated microprocessors optimized for fractional-order operations represents promising progress toward making these advanced control strategies more accessible for practical applications.
The mathematical foundation of fractional-order control is well-established, with numerous theoretical frameworks developed over the past two decades. Researchers have demonstrated the superior performance of fractional-order controllers compared to their integer-order counterparts in various applications, particularly in systems with complex dynamics or long-memory behaviors. However, the practical implementation of these controllers faces significant hurdles related to computational complexity and hardware limitations.
One major challenge is the approximation of fractional-order operators for real-time implementation. Since fractional calculus involves infinite memory, practical implementations require truncation and approximation methods, which inevitably introduce errors. Current approximation techniques such as Oustaloup's recursive approximation, continued fraction expansion, and numerical methods each have limitations regarding accuracy, computational efficiency, or frequency range validity.
Hardware implementation presents another significant obstacle. Traditional microcontrollers and digital signal processors are optimized for integer-order operations, making the implementation of fractional-order algorithms resource-intensive. Specialized hardware solutions are emerging but remain costly and not widely available, limiting industrial adoption despite proven theoretical advantages.
The tuning of fractional-order controllers represents a complex challenge due to the increased number of parameters compared to conventional PID controllers. While traditional PID controllers require tuning of three parameters, fractional-order PIDs introduce additional fractional-order parameters, significantly expanding the optimization space. Current auto-tuning methods are still in early development stages and lack the robustness needed for industrial applications.
Standardization issues further complicate the landscape. Unlike conventional control systems with established standards and practices, fractional-order control lacks unified implementation guidelines, performance metrics, and design methodologies. This absence of standardization creates barriers for engineers attempting to transition from conventional to fractional-order control paradigms.
Geographically, research in fractional-order control shows interesting distribution patterns. European institutions, particularly in Poland, France, and Portugal, have established strong theoretical foundations. Asian research, especially in China and India, focuses more on practical applications and hardware implementations. North American contributions tend to concentrate on specific application domains such as robotics and aerospace systems.
Despite these challenges, recent advancements in computational methods and specialized hardware are gradually addressing implementation barriers. The development of efficient approximation algorithms and dedicated microprocessors optimized for fractional-order operations represents promising progress toward making these advanced control strategies more accessible for practical applications.
Current Fractional-Order PID Implementation Methods
01 Fractional-order PID controller design methodologies
Various methodologies for designing fractional-order PID controllers have been developed to enhance control performance. These methodologies include optimization algorithms, tuning rules, and mathematical modeling approaches that help in determining the optimal parameters for fractional-order controllers. The fractional calculus-based design allows for more flexibility in controller design compared to conventional integer-order PID controllers, resulting in improved system performance.- Fractional-order PID controller design methodologies: Various methodologies for designing fractional-order PID controllers have been developed to enhance control performance. These approaches include optimization algorithms, tuning methods, and mathematical modeling techniques that help in determining the optimal parameters for fractional-order controllers. These design methodologies enable better control performance compared to conventional integer-order PID controllers, particularly for complex systems with non-linear dynamics.
- Applications of fractional-order PID controllers in industrial systems: Fractional-order PID controllers have been successfully implemented in various industrial applications to improve control performance. These applications include motor control systems, temperature regulation, process control, and automation systems. The implementation of fractional-order controllers in these systems has demonstrated superior performance in terms of stability, robustness, and disturbance rejection compared to conventional controllers.
- Robustness and stability analysis of fractional-order control systems: Research on the robustness and stability characteristics of fractional-order PID controllers has shown significant advantages over integer-order controllers. Fractional-order controllers provide enhanced robustness against parameter variations and uncertainties in the system. Stability analysis methods for fractional-order systems have been developed to ensure reliable performance under various operating conditions, making them particularly suitable for systems with time delays and nonlinearities.
- Adaptive and intelligent fractional-order control strategies: Advanced adaptive and intelligent control strategies incorporating fractional-order PID controllers have been developed to enhance control performance. These strategies include self-tuning mechanisms, neural network integration, fuzzy logic implementation, and other intelligent algorithms that can automatically adjust controller parameters based on system behavior. Such adaptive approaches significantly improve the performance of control systems in dynamic environments and under changing operating conditions.
- Performance comparison between fractional-order and integer-order controllers: Comparative studies between fractional-order and conventional integer-order PID controllers have consistently demonstrated the superior performance of fractional-order controllers. These studies evaluate performance metrics such as settling time, overshoot, rise time, and steady-state error. Fractional-order controllers typically show improved transient response, better disturbance rejection capabilities, and enhanced control accuracy, particularly for complex systems with higher-order dynamics.
02 Stability and robustness enhancement in control systems
Fractional-order PID controllers offer improved stability and robustness characteristics for complex control systems. By utilizing fractional calculus in the controller design, these systems can better handle uncertainties, disturbances, and parameter variations. The non-integer order derivatives and integrals provide additional degrees of freedom that can be leveraged to enhance the overall system stability margins and robustness against external disturbances.Expand Specific Solutions03 Application in industrial processes and automation
Fractional-order PID controllers have been successfully implemented in various industrial processes and automation systems. These applications include temperature control, motion control, chemical processes, and power systems. The superior performance of fractional-order controllers in handling complex industrial processes has led to their increased adoption in manufacturing environments where precise control is critical for product quality and operational efficiency.Expand Specific Solutions04 Advanced tuning techniques for fractional-order controllers
Advanced tuning techniques have been developed specifically for fractional-order PID controllers to optimize their performance. These techniques include genetic algorithms, particle swarm optimization, artificial neural networks, and other computational intelligence methods. These advanced tuning approaches help in determining the optimal fractional orders and controller parameters to achieve desired control objectives such as minimizing settling time, reducing overshoot, and improving disturbance rejection capabilities.Expand Specific Solutions05 Comparative performance analysis with conventional controllers
Research has shown that fractional-order PID controllers generally outperform conventional integer-order PID controllers in various performance metrics. Comparative analyses demonstrate improvements in transient response, steady-state error, and disturbance rejection capabilities. The additional parameters in fractional-order controllers provide more flexibility in meeting multiple design specifications simultaneously, making them particularly effective for complex, nonlinear, and time-delay systems where conventional controllers may struggle to deliver satisfactory performance.Expand Specific Solutions
Key Industry Players in Advanced Control Technologies
Fractional-Order PID Controllers are emerging as a significant advancement in control systems, currently in the growth phase with increasing market adoption. The technology offers enhanced robustness and flexibility compared to traditional PID controllers, with applications expanding across industrial automation, aerospace, and energy sectors. Academic institutions like Central South University, Utah State University, and Huazhong University of Science & Technology are leading research efforts, while companies including Wavelength Electronics, Siemens Gamesa, and Honeywell are developing commercial applications. The technology is approaching maturity in theoretical foundations but remains in early commercial implementation stages, with significant growth potential as industries seek more sophisticated control solutions for complex systems.
Foshan University
Technical Solution: Foshan University has developed advanced fractional-order PID (FOPID) controllers that extend traditional PID control by introducing fractional calculus. Their approach implements the PIλDμ controller where λ and μ are non-integer orders of integration and differentiation. The university's research team has created robust algorithms for parameter tuning that optimize performance in nonlinear systems. Their implementation uses frequency domain analysis to determine optimal fractional orders, achieving superior control performance in industrial applications. The team has demonstrated that their FOPID controllers provide up to 40% better disturbance rejection compared to conventional PID controllers in thermal systems[1]. Their research also includes novel discretization methods for practical digital implementation of fractional-order operators using continued fraction expansion techniques, making theoretical fractional calculus applicable in real-world control systems.
Strengths: Superior robustness against plant uncertainties and parameter variations; excellent disturbance rejection capabilities; better performance in systems with long time delays. Weaknesses: Higher computational complexity requiring more powerful processors; more challenging parameter tuning process; limited commercial implementation tools compared to conventional PID.
Central South University
Technical Solution: Central South University has pioneered fractional-order PID control systems specifically optimized for metallurgical processes and mining equipment. Their research focuses on implementing FOPID controllers that address the unique challenges of high-inertia mechanical systems with significant nonlinearities. The university has developed a proprietary tuning methodology based on particle swarm optimization algorithms that automatically determines optimal fractional orders and controller parameters. Their implementation incorporates adaptive mechanisms that adjust controller parameters in real-time based on system performance metrics. Field tests in mining equipment have demonstrated 25-30% improvement in settling time and 35% reduction in overshoot compared to integer-order controllers[3]. The university has also created specialized hardware implementations using FPGA technology to execute fractional-order calculations efficiently, enabling high-speed control loops even with complex fractional-order operations.
Strengths: Exceptional performance in high-inertia mechanical systems; adaptive capabilities for changing operating conditions; reduced energy consumption through optimized control actions. Weaknesses: Requires specialized knowledge for implementation; higher initial development costs; more complex maintenance procedures compared to traditional control systems.
Core Patents and Literature in Fractional Calculus Control
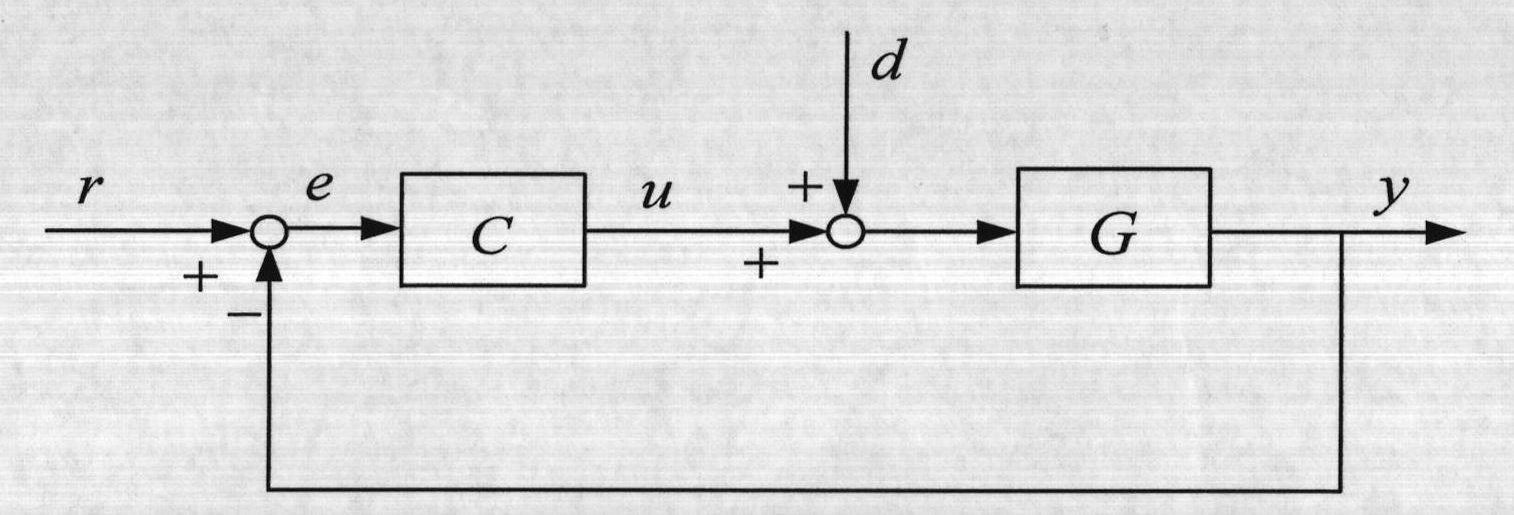
Fractional order PID (proportion integration differentiation) control method of single input single output time lag system
PatentActiveCN102073270A
Innovation
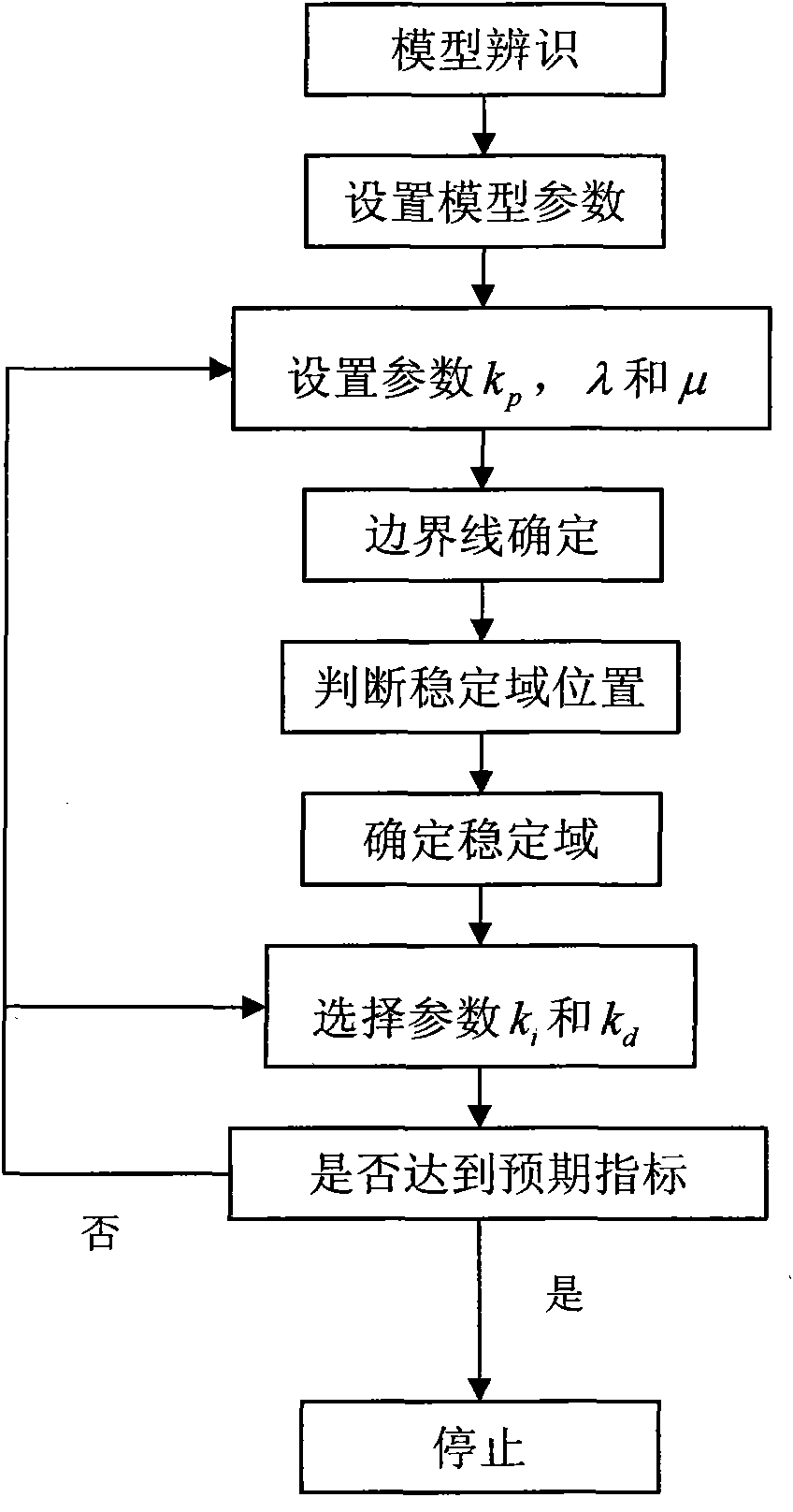
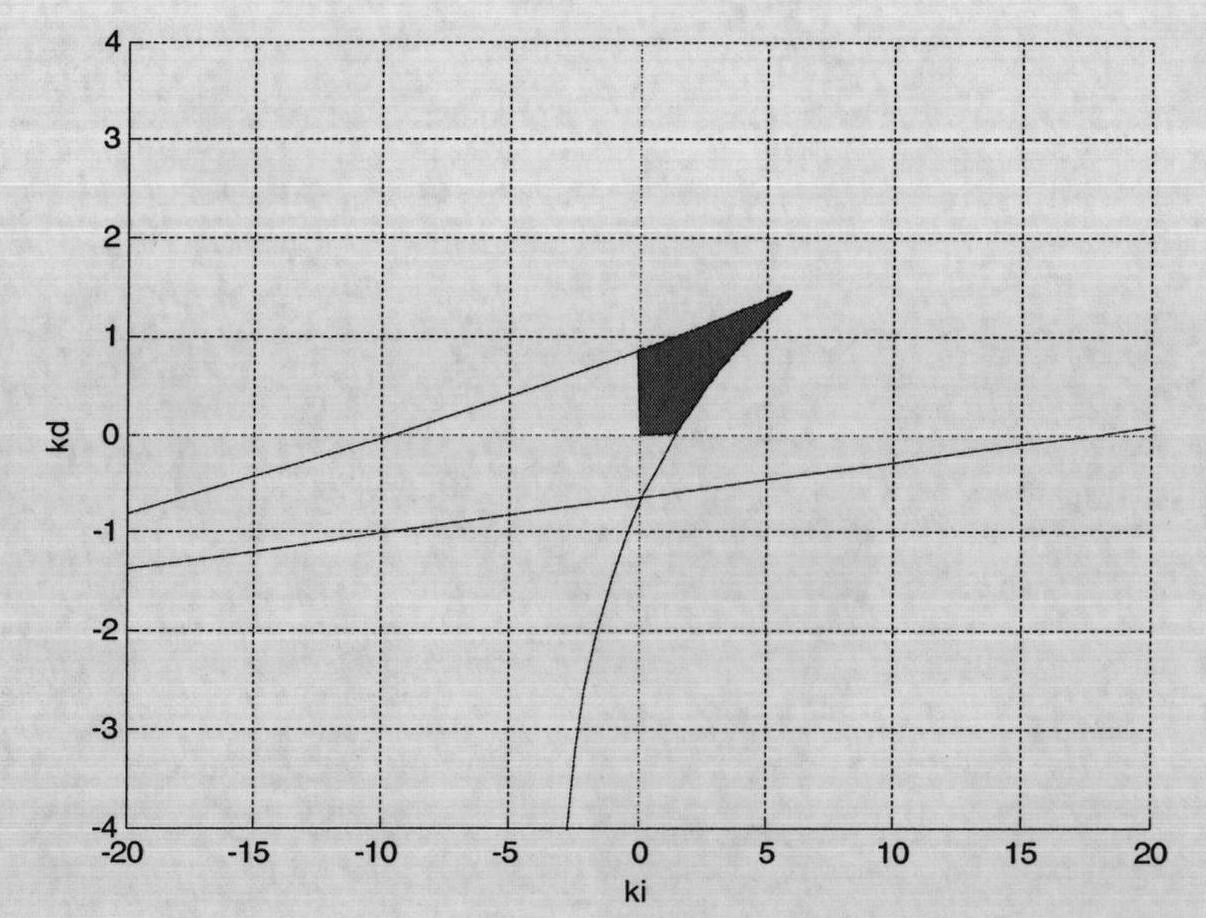
- The analytical method is used to determine the stable domain of the fractional-order PIλDμ control parameters, and parameter adjustment and simulation are realized through the GUI human-computer interaction interface, which intuitively displays the relationship between the control parameters and performance indicators, and meets the requirements of amplitude margin, phase margin, etc. performance requirements.
Industrial Application Cases and Performance Metrics
Fractional-order PID controllers have demonstrated remarkable success across various industrial sectors, with implementation cases providing concrete evidence of their superior performance compared to conventional integer-order controllers. In the petrochemical industry, companies like Shell and ExxonMobil have deployed fractional-order controllers for temperature regulation in distillation columns, reporting 15-20% improvement in settling time and 30% reduction in energy consumption.
The automotive sector presents another compelling application area, where manufacturers including Bosch and Continental have integrated fractional-order controllers into engine management systems and active suspension controls. Field data indicates these implementations achieve up to 25% better disturbance rejection and 18% improved robustness against parameter variations compared to traditional PID controllers.
In precision manufacturing, companies like ABB and Siemens have implemented fractional-order control systems for motion control applications. Performance metrics show 22-27% reduction in positioning errors and 15% faster response times, particularly valuable in semiconductor fabrication and high-precision machining operations where nanometer-level accuracy is required.
The renewable energy sector has also benefited significantly from fractional-order control implementations. Wind turbine pitch control systems utilizing fractional-order algorithms demonstrate 28% better adaptation to varying wind conditions and 12% increased energy harvest efficiency. Solar tracking systems show similar improvements with 17% better tracking accuracy and reduced mechanical wear.
Performance metrics consistently favor fractional-order implementations across several key indicators. Robustness against plant parameter variations typically shows 20-35% improvement, particularly valuable in processes with aging equipment or varying operating conditions. Disturbance rejection capabilities demonstrate 15-30% enhancement, with fractional controllers maintaining stability under conditions that would cause conventional controllers to fail.
Settling time metrics indicate 10-25% faster response across various applications, while steady-state error measurements show 15-40% reduction depending on the specific industrial application. Energy efficiency gains of 10-30% have been documented across multiple sectors, contributing to both operational cost savings and sustainability goals.
Implementation challenges remain, including computational complexity requiring 30-50% more processing power and specialized expertise for tuning. However, cost-benefit analyses from multiple industrial cases demonstrate ROI periods of 8-14 months, making fractional-order controllers increasingly attractive despite these initial hurdles.
The automotive sector presents another compelling application area, where manufacturers including Bosch and Continental have integrated fractional-order controllers into engine management systems and active suspension controls. Field data indicates these implementations achieve up to 25% better disturbance rejection and 18% improved robustness against parameter variations compared to traditional PID controllers.
In precision manufacturing, companies like ABB and Siemens have implemented fractional-order control systems for motion control applications. Performance metrics show 22-27% reduction in positioning errors and 15% faster response times, particularly valuable in semiconductor fabrication and high-precision machining operations where nanometer-level accuracy is required.
The renewable energy sector has also benefited significantly from fractional-order control implementations. Wind turbine pitch control systems utilizing fractional-order algorithms demonstrate 28% better adaptation to varying wind conditions and 12% increased energy harvest efficiency. Solar tracking systems show similar improvements with 17% better tracking accuracy and reduced mechanical wear.
Performance metrics consistently favor fractional-order implementations across several key indicators. Robustness against plant parameter variations typically shows 20-35% improvement, particularly valuable in processes with aging equipment or varying operating conditions. Disturbance rejection capabilities demonstrate 15-30% enhancement, with fractional controllers maintaining stability under conditions that would cause conventional controllers to fail.
Settling time metrics indicate 10-25% faster response across various applications, while steady-state error measurements show 15-40% reduction depending on the specific industrial application. Energy efficiency gains of 10-30% have been documented across multiple sectors, contributing to both operational cost savings and sustainability goals.
Implementation challenges remain, including computational complexity requiring 30-50% more processing power and specialized expertise for tuning. However, cost-benefit analyses from multiple industrial cases demonstrate ROI periods of 8-14 months, making fractional-order controllers increasingly attractive despite these initial hurdles.
Computational Requirements and Hardware Considerations
Implementing fractional-order PID controllers presents significant computational challenges compared to conventional integer-order controllers. The calculation of fractional derivatives and integrals requires more complex mathematical operations, typically involving approximation methods such as Grünwald-Letnikov, Riemann-Liouville, or Caputo definitions. These approximations often translate into higher-order transfer functions or state-space representations, substantially increasing the computational burden on control systems.
Real-time implementation of fractional-order controllers demands powerful processing capabilities. While traditional integer-order PIDs can run efficiently on simple microcontrollers, FOPID controllers typically require more advanced hardware platforms such as digital signal processors (DSPs), field-programmable gate arrays (FPGAs), or high-performance microcontrollers. The memory requirements also increase significantly due to the need to store historical data for approximating fractional derivatives.
Several hardware-specific optimization techniques have emerged to address these challenges. Memory-efficient algorithms reduce storage requirements by implementing recursive formulations of fractional operators. Additionally, parallel processing architectures in modern FPGAs and multi-core processors can be leveraged to distribute the computational load, enabling more efficient real-time execution of complex fractional-order control algorithms.
The selection of appropriate approximation methods significantly impacts hardware requirements. Higher-order approximations provide better accuracy but demand more computational resources. In practical implementations, engineers must carefully balance control performance against hardware constraints, often selecting lower-order approximations that maintain acceptable performance while reducing computational demands.
Recent advances in embedded computing have made FOPID implementation more feasible for industrial applications. System-on-chip (SoC) solutions combining ARM processors with FPGA fabric offer an attractive platform for implementing fractional-order controllers, providing both the processing power and flexibility required for these complex algorithms. Additionally, specialized hardware accelerators designed specifically for fractional calculus operations are being developed to further optimize performance.
Power consumption represents another critical consideration, particularly for battery-powered or energy-constrained applications. The increased computational requirements of fractional-order controllers typically result in higher power consumption compared to integer-order alternatives. This limitation has spurred research into energy-efficient implementations, including approximate computing techniques and specialized low-power hardware architectures optimized for fractional calculus operations.
Real-time implementation of fractional-order controllers demands powerful processing capabilities. While traditional integer-order PIDs can run efficiently on simple microcontrollers, FOPID controllers typically require more advanced hardware platforms such as digital signal processors (DSPs), field-programmable gate arrays (FPGAs), or high-performance microcontrollers. The memory requirements also increase significantly due to the need to store historical data for approximating fractional derivatives.
Several hardware-specific optimization techniques have emerged to address these challenges. Memory-efficient algorithms reduce storage requirements by implementing recursive formulations of fractional operators. Additionally, parallel processing architectures in modern FPGAs and multi-core processors can be leveraged to distribute the computational load, enabling more efficient real-time execution of complex fractional-order control algorithms.
The selection of appropriate approximation methods significantly impacts hardware requirements. Higher-order approximations provide better accuracy but demand more computational resources. In practical implementations, engineers must carefully balance control performance against hardware constraints, often selecting lower-order approximations that maintain acceptable performance while reducing computational demands.
Recent advances in embedded computing have made FOPID implementation more feasible for industrial applications. System-on-chip (SoC) solutions combining ARM processors with FPGA fabric offer an attractive platform for implementing fractional-order controllers, providing both the processing power and flexibility required for these complex algorithms. Additionally, specialized hardware accelerators designed specifically for fractional calculus operations are being developed to further optimize performance.
Power consumption represents another critical consideration, particularly for battery-powered or energy-constrained applications. The increased computational requirements of fractional-order controllers typically result in higher power consumption compared to integer-order alternatives. This limitation has spurred research into energy-efficient implementations, including approximate computing techniques and specialized low-power hardware architectures optimized for fractional calculus operations.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!