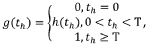Laplace Domain Analysis Of PID Control System Dynamics
SEP 8, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
PID Control System Fundamentals and Objectives
Proportional-Integral-Derivative (PID) control systems represent one of the most fundamental and widely implemented control methodologies in industrial applications. The evolution of PID control traces back to the early 20th century, with significant theoretical developments occurring during the 1940s and 1950s when Laplace transform techniques were increasingly applied to control system analysis. This mathematical approach revolutionized how engineers understood and designed feedback control systems by transforming complex time-domain differential equations into more manageable algebraic expressions.
The core principle of PID control lies in its three-term functionality: the proportional term provides immediate response to current error, the integral term addresses accumulated past errors, and the derivative term anticipates future errors based on the rate of change. When analyzed in the Laplace domain, these components translate to specific transfer functions that can be systematically studied and optimized for various applications.
Recent technological trends in PID control systems include adaptive PID algorithms that automatically tune parameters based on system response, fractional-order PID controllers offering enhanced flexibility through non-integer order derivatives and integrals, and model predictive control strategies that incorporate PID principles within more sophisticated predictive frameworks. These advancements reflect the ongoing evolution of control theory to address increasingly complex industrial requirements.
The Laplace domain analysis of PID control systems provides critical insights into system stability, transient response characteristics, and steady-state behavior. By examining the location of poles and zeros in the complex plane, engineers can predict system performance and design controllers that meet specific requirements for overshoot, settling time, and steady-state error. This mathematical framework enables the systematic design of control systems across diverse applications.
The primary technical objectives of PID control system analysis in the Laplace domain include: establishing robust stability criteria for closed-loop systems, optimizing controller parameters to achieve desired performance metrics, developing analytical methods for handling system nonlinearities and uncertainties, and creating standardized approaches for controller design across various industrial applications. These objectives drive ongoing research and development in control theory.
As industrial systems become increasingly complex and interconnected, the integration of classical PID control principles with modern computational techniques represents a significant trend. Machine learning algorithms are being employed to optimize PID parameters in real-time, while digital twin technologies enable sophisticated simulation and testing of control strategies before deployment. These developments point toward a future where traditional PID control theory merges with advanced computational methods to address the challenges of Industry 4.0 environments.
The core principle of PID control lies in its three-term functionality: the proportional term provides immediate response to current error, the integral term addresses accumulated past errors, and the derivative term anticipates future errors based on the rate of change. When analyzed in the Laplace domain, these components translate to specific transfer functions that can be systematically studied and optimized for various applications.
Recent technological trends in PID control systems include adaptive PID algorithms that automatically tune parameters based on system response, fractional-order PID controllers offering enhanced flexibility through non-integer order derivatives and integrals, and model predictive control strategies that incorporate PID principles within more sophisticated predictive frameworks. These advancements reflect the ongoing evolution of control theory to address increasingly complex industrial requirements.
The Laplace domain analysis of PID control systems provides critical insights into system stability, transient response characteristics, and steady-state behavior. By examining the location of poles and zeros in the complex plane, engineers can predict system performance and design controllers that meet specific requirements for overshoot, settling time, and steady-state error. This mathematical framework enables the systematic design of control systems across diverse applications.
The primary technical objectives of PID control system analysis in the Laplace domain include: establishing robust stability criteria for closed-loop systems, optimizing controller parameters to achieve desired performance metrics, developing analytical methods for handling system nonlinearities and uncertainties, and creating standardized approaches for controller design across various industrial applications. These objectives drive ongoing research and development in control theory.
As industrial systems become increasingly complex and interconnected, the integration of classical PID control principles with modern computational techniques represents a significant trend. Machine learning algorithms are being employed to optimize PID parameters in real-time, while digital twin technologies enable sophisticated simulation and testing of control strategies before deployment. These developments point toward a future where traditional PID control theory merges with advanced computational methods to address the challenges of Industry 4.0 environments.
Industrial Applications and Market Demand for PID Controllers
The global market for PID controllers continues to demonstrate robust growth, driven primarily by increasing industrial automation across various sectors. Current market analysis indicates that the industrial automation market, where PID controllers are essential components, is valued at approximately $191 billion and projected to reach $265 billion by 2025, representing a compound annual growth rate of 6.7%. Within this broader market, PID controllers constitute a significant segment due to their versatility and reliability in process control applications.
Manufacturing industries, particularly in automotive, chemical processing, and food and beverage sectors, exhibit the highest demand for PID control systems. These industries require precise temperature, pressure, and flow control to maintain product quality and operational efficiency. The automotive manufacturing sector alone has increased its automation investment by 8.3% annually, with PID controllers featuring prominently in assembly line operations and quality control systems.
Energy management represents another substantial market for PID controllers, particularly in HVAC systems and renewable energy installations. The global push toward energy efficiency has accelerated the adoption of sophisticated control systems, with the smart building market growing at 12.1% annually. PID controllers are integral to these systems, optimizing energy consumption while maintaining comfort parameters.
The healthcare and pharmaceutical industries have emerged as rapidly expanding markets for precision control systems. Manufacturing facilities in these sectors must maintain extremely tight tolerances for temperature, humidity, and pressure in clean rooms and production environments. This sector's demand for advanced PID controllers has grown by 9.4% annually, driven by increasingly stringent regulatory requirements.
Regional analysis reveals that Asia-Pacific represents the fastest-growing market for industrial automation and control systems, with China, Japan, and South Korea leading implementation. North America and Europe maintain significant market shares, with emphasis on upgrading legacy systems to more sophisticated digital PID controllers with enhanced features like self-tuning capabilities and network connectivity.
Customer requirements are evolving toward more integrated solutions, with 78% of industrial customers preferring PID controllers that offer seamless integration with Industrial Internet of Things (IIoT) platforms. This trend is driving development of controllers with enhanced communication protocols, remote monitoring capabilities, and predictive maintenance features. Additionally, there is increasing demand for controllers that can handle complex, non-linear processes through adaptive algorithms and machine learning enhancements.
Manufacturing industries, particularly in automotive, chemical processing, and food and beverage sectors, exhibit the highest demand for PID control systems. These industries require precise temperature, pressure, and flow control to maintain product quality and operational efficiency. The automotive manufacturing sector alone has increased its automation investment by 8.3% annually, with PID controllers featuring prominently in assembly line operations and quality control systems.
Energy management represents another substantial market for PID controllers, particularly in HVAC systems and renewable energy installations. The global push toward energy efficiency has accelerated the adoption of sophisticated control systems, with the smart building market growing at 12.1% annually. PID controllers are integral to these systems, optimizing energy consumption while maintaining comfort parameters.
The healthcare and pharmaceutical industries have emerged as rapidly expanding markets for precision control systems. Manufacturing facilities in these sectors must maintain extremely tight tolerances for temperature, humidity, and pressure in clean rooms and production environments. This sector's demand for advanced PID controllers has grown by 9.4% annually, driven by increasingly stringent regulatory requirements.
Regional analysis reveals that Asia-Pacific represents the fastest-growing market for industrial automation and control systems, with China, Japan, and South Korea leading implementation. North America and Europe maintain significant market shares, with emphasis on upgrading legacy systems to more sophisticated digital PID controllers with enhanced features like self-tuning capabilities and network connectivity.
Customer requirements are evolving toward more integrated solutions, with 78% of industrial customers preferring PID controllers that offer seamless integration with Industrial Internet of Things (IIoT) platforms. This trend is driving development of controllers with enhanced communication protocols, remote monitoring capabilities, and predictive maintenance features. Additionally, there is increasing demand for controllers that can handle complex, non-linear processes through adaptive algorithms and machine learning enhancements.
Current Laplace Domain Analysis Methods and Limitations
Laplace domain analysis has become the cornerstone of modern control system design, particularly for PID controllers due to its ability to transform complex differential equations into algebraic expressions. The current methodologies primarily revolve around transfer function analysis, frequency response techniques, and stability criteria evaluation.
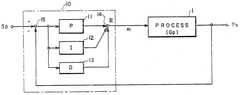
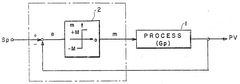
Transfer function representation forms the foundation of Laplace domain analysis for PID systems. Engineers typically express the controller in the standard form C(s) = Kp + Ki/s + Kds, where Kp, Ki, and Kd represent the proportional, integral, and derivative gains respectively. This mathematical model allows for straightforward algebraic manipulation when combined with plant models to analyze closed-loop behavior.
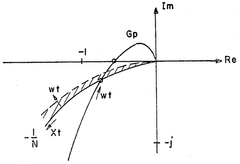
Root locus techniques remain one of the most widely utilized methods, enabling visualization of how poles migrate as control parameters change. This approach provides intuitive insights into stability margins and transient response characteristics. Complementary to this, Bode and Nyquist plots offer frequency domain perspectives that reveal crucial information about system bandwidth, phase margin, and gain margin.
State-space representation in the Laplace domain has gained prominence for complex MIMO systems, though its application to classical PID analysis often introduces unnecessary complexity. The conversion between transfer function and state-space models, while mathematically sound, sometimes obscures the direct relationship between PID parameters and system performance.
Despite these powerful tools, current Laplace domain methods face significant limitations. The linearization requirement presents a fundamental constraint, as real-world PID systems frequently operate in nonlinear regimes where superposition principles no longer apply. This necessitates multiple operating point analyses or more complex describing function approaches.
Time-delay systems pose another substantial challenge. While Padé approximations offer workable solutions for systems with small delays, they become increasingly inaccurate for larger delays, potentially leading to erroneous stability predictions in PID tuning applications.
Computational complexity escalates rapidly for higher-order systems, making analytical solutions impractical. Numerical methods often become necessary, but these introduce approximation errors that can propagate through the analysis. Additionally, parameter uncertainty and variation remain inadequately addressed by classical Laplace techniques, requiring supplementary robust control methodologies.
Modern industrial applications frequently involve distributed parameter systems where the traditional lumped-parameter assumptions break down. The resulting partial differential equations do not map cleanly to standard Laplace domain representations, necessitating spatial discretization that introduces additional modeling errors.
These limitations have spurred research into hybrid approaches that combine Laplace techniques with time-domain simulations, numerical optimization, and machine learning algorithms to overcome the inherent constraints of pure analytical methods.
Transfer function representation forms the foundation of Laplace domain analysis for PID systems. Engineers typically express the controller in the standard form C(s) = Kp + Ki/s + Kds, where Kp, Ki, and Kd represent the proportional, integral, and derivative gains respectively. This mathematical model allows for straightforward algebraic manipulation when combined with plant models to analyze closed-loop behavior.
Root locus techniques remain one of the most widely utilized methods, enabling visualization of how poles migrate as control parameters change. This approach provides intuitive insights into stability margins and transient response characteristics. Complementary to this, Bode and Nyquist plots offer frequency domain perspectives that reveal crucial information about system bandwidth, phase margin, and gain margin.
State-space representation in the Laplace domain has gained prominence for complex MIMO systems, though its application to classical PID analysis often introduces unnecessary complexity. The conversion between transfer function and state-space models, while mathematically sound, sometimes obscures the direct relationship between PID parameters and system performance.
Despite these powerful tools, current Laplace domain methods face significant limitations. The linearization requirement presents a fundamental constraint, as real-world PID systems frequently operate in nonlinear regimes where superposition principles no longer apply. This necessitates multiple operating point analyses or more complex describing function approaches.
Time-delay systems pose another substantial challenge. While Padé approximations offer workable solutions for systems with small delays, they become increasingly inaccurate for larger delays, potentially leading to erroneous stability predictions in PID tuning applications.
Computational complexity escalates rapidly for higher-order systems, making analytical solutions impractical. Numerical methods often become necessary, but these introduce approximation errors that can propagate through the analysis. Additionally, parameter uncertainty and variation remain inadequately addressed by classical Laplace techniques, requiring supplementary robust control methodologies.
Modern industrial applications frequently involve distributed parameter systems where the traditional lumped-parameter assumptions break down. The resulting partial differential equations do not map cleanly to standard Laplace domain representations, necessitating spatial discretization that introduces additional modeling errors.
These limitations have spurred research into hybrid approaches that combine Laplace techniques with time-domain simulations, numerical optimization, and machine learning algorithms to overcome the inherent constraints of pure analytical methods.
Modern Laplace Transform Techniques for PID Systems
01 PID Control for Engine and Combustion Systems
PID control systems are implemented in engine management and combustion systems to optimize performance and efficiency. These systems monitor parameters such as air-fuel ratio, throttle position, and exhaust gas recirculation to maintain optimal engine operation. The control algorithms adjust in real-time to changing conditions, providing precise control over combustion processes and emissions while ensuring system stability across various operating conditions.- PID control for engine and combustion systems: PID control systems are implemented in engine management and combustion systems to optimize performance and efficiency. These control systems monitor and adjust parameters such as fuel injection timing, air-fuel ratio, and throttle position in real-time. By implementing dynamic feedback loops, these systems can respond to changing operating conditions while maintaining stability and performance targets. Advanced implementations may include adaptive tuning to account for engine wear and environmental variations.
- Adaptive and self-tuning PID control methodologies: Adaptive PID control systems can automatically adjust their parameters based on system response and changing conditions. These self-tuning methodologies analyze system dynamics in real-time to optimize proportional, integral, and derivative gains without manual intervention. Such systems can identify changes in process characteristics and modify control parameters accordingly, improving robustness against disturbances and parameter variations. This approach is particularly valuable in systems with non-linear dynamics or time-varying parameters.
- PID control for precision motion and positioning systems: PID controllers are implemented in precision motion and positioning systems to achieve accurate and stable control. These systems utilize feedback from position sensors to calculate appropriate control signals for motors or actuators. The control algorithms balance response speed with stability requirements while minimizing overshoot and steady-state error. Advanced implementations may incorporate feed-forward elements and friction compensation to improve dynamic performance in applications requiring high precision movement control.
- Digital implementation and optimization of PID control systems: Digital implementations of PID control systems offer enhanced flexibility and performance compared to analog counterparts. These systems leverage microprocessors or specialized hardware to execute control algorithms with high precision and sampling rates. Digital implementations enable advanced features such as gain scheduling, anti-windup mechanisms, and filter optimization to improve system dynamics. The discretization methods and sampling frequency selection significantly impact the control system performance and stability characteristics.
- PID control for complex industrial processes and systems: PID control systems are applied to complex industrial processes to maintain desired operating conditions and product quality. These implementations often feature cascaded control loops, where multiple PID controllers work together to manage interdependent process variables. The control architecture may incorporate model-based elements to handle process delays and non-linearities. System identification techniques are used to characterize process dynamics and optimize controller parameters for specific operating regimes, ensuring robust performance across varying production conditions.
02 Advanced PID Tuning and Adaptation Techniques
Advanced methods for tuning and adapting PID controllers improve system performance across varying conditions. These techniques include auto-tuning algorithms, adaptive control strategies, and model-based parameter optimization. By dynamically adjusting controller parameters based on system response and environmental changes, these methods enhance control accuracy, reduce settling time, and minimize overshoot in complex dynamic systems.Expand Specific Solutions03 PID Control in Power Generation and Distribution
PID control systems play a crucial role in power generation and distribution networks by regulating voltage, frequency, and power flow. These control systems maintain grid stability through continuous monitoring and adjustment of power parameters. The implementation includes feedback mechanisms that respond to load variations and system disturbances, ensuring reliable operation of power systems under varying demand conditions.Expand Specific Solutions04 Integration of PID Control with Digital Systems and Networks
Modern PID control systems are increasingly integrated with digital networks and communication protocols to enhance monitoring and control capabilities. These networked control systems enable remote operation, data collection, and system diagnostics. The integration facilitates coordinated control of multiple subsystems, improves fault detection, and allows for more sophisticated control strategies through distributed processing and cloud-based analytics.Expand Specific Solutions05 PID Control for Precision Motion and Positioning Systems
PID controllers are essential in precision motion and positioning systems where accurate movement control is critical. These applications include robotics, manufacturing equipment, and vehicle dynamics control. The control algorithms compensate for mechanical nonlinearities, friction, and external disturbances to achieve precise positioning. Advanced implementations incorporate feedforward control and multi-loop structures to improve tracking performance and disturbance rejection.Expand Specific Solutions
Leading Research Institutions and Industrial Players
The Laplace Domain Analysis of PID Control System Dynamics market is in a mature growth phase, characterized by established theoretical frameworks and widespread industrial applications. The market size is substantial, estimated in the billions due to PID controllers' ubiquity across manufacturing, aerospace, and automotive sectors. Technologically, academic institutions like Beihang University, Tianjin University, and National University of Singapore lead theoretical research, while industrial players demonstrate varying maturity levels. Companies like National Instruments and Fraunhofer-Gesellschaft offer sophisticated commercial solutions with advanced Laplace-based modeling tools. Manufacturers such as Toyota Motor Corp. and Yamaha Motor integrate these systems into production processes, while specialized automation firms like Sodick and LSIS develop industry-specific implementations, creating a competitive ecosystem balancing theoretical innovation and practical application.
National University of Singapore
Technical Solution: The National University of Singapore (NUS) has developed significant research contributions in Laplace domain analysis of PID control systems through their Advanced Control Technology Laboratory. Their approach focuses on mathematical rigor combined with practical applications, particularly in addressing nonlinear system dynamics through linearization techniques in the Laplace domain. NUS researchers have pioneered methods for fractional-order PID controllers, extending traditional integer-order calculus to fractional calculus in the Laplace domain, which provides additional degrees of freedom for controller design and improved performance for certain classes of systems. Their work includes novel stability analysis techniques that combine classical Routh-Hurwitz criteria with advanced frequency domain methods to establish robust stability guarantees for complex industrial systems. NUS has also developed adaptive tuning algorithms that utilize real-time system identification in the Laplace domain to continuously optimize controller parameters in response to changing process dynamics or disturbances. Their research extends to multivariable PID control systems, addressing the challenges of loop interactions through decoupling techniques based on transfer function matrices and frequency response analysis. The university has established industry partnerships to implement these theoretical advances in practical applications ranging from precision manufacturing to biomedical systems.
Strengths: Strong theoretical foundation with rigorous mathematical proofs; innovative approaches to complex control problems; extensive peer-reviewed publications establishing academic credibility. Weaknesses: Some solutions may prioritize theoretical elegance over practical implementation concerns; research prototypes may require significant engineering effort to transition to commercial applications.
Toyota Motor Corp.
Technical Solution: Toyota has pioneered advanced PID control methodologies for automotive applications through their Laplace domain analysis framework. Their approach centers on developing transfer function models that accurately represent vehicle dynamics across multiple subsystems, from engine management to suspension control. Toyota's proprietary control algorithms utilize pole-zero placement techniques in the s-domain to achieve precise stability margins while maintaining robust performance under varying operating conditions. The company has implemented adaptive PID controllers that continuously adjust parameters based on real-time frequency response analysis, enabling optimal performance across diverse driving scenarios. Toyota's control systems incorporate feed-forward compensation elements derived from Laplace domain modeling to mitigate disturbances before they affect vehicle behavior. Their methodology includes comprehensive stability analysis using Nyquist and Bode techniques to ensure safe operation even when component characteristics change due to aging or environmental factors. Toyota has also developed specialized state-space representations that complement traditional Laplace methods for their hybrid powertrain systems, allowing seamless transitions between different operating modes while maintaining stable control.
Strengths: Exceptional robustness in real-world applications; sophisticated disturbance rejection capabilities; highly optimized for automotive-specific requirements. Weaknesses: Highly proprietary solutions with limited external documentation; primarily focused on automotive applications rather than general control theory advancement.
Key Mathematical Frameworks and Transfer Functions
Methods of proportional-integral-derivative control
PatentWO2019076881A3
Innovation
- Dynamic adjustment of integral or derivative gain based on both setpoint and state variable, which enhances control system adaptability compared to traditional fixed-gain PID controllers.
- The method provides a more responsive control system by considering the current system state and desired setpoint when calculating integral or derivative gains, potentially reducing overshoot and settling time.
- The approach maintains the simplicity of traditional PID control while incorporating adaptive elements, making it suitable for implementation in existing control systems with minimal modifications.
Method of determining PID parameters and an automatic tuning controller using the method
PatentInactiveUS4754391A
Innovation
- A method that monitors a limit cycle generated in a process by inserting a nonlinear element into the PID controller's proportional operation portion and connecting the integral operation portion in parallel, allowing for continuous process control and determination of optimum PID parameters without disrupting normal operation.
Stability Analysis and Performance Metrics
Stability analysis in PID control systems represents a critical aspect of control engineering, particularly when examined through Laplace domain techniques. The Routh-Hurwitz criterion provides a systematic approach for determining stability without explicitly solving for the roots of the characteristic equation. When applied to PID-controlled systems, this method efficiently identifies the range of controller parameters that ensure system stability, forming the foundation for subsequent performance optimization.
Performance metrics for PID control systems can be directly derived from the Laplace domain representation. The transient response characteristics—including rise time, settling time, and percentage overshoot—are quantifiable through the system's poles and zeros configuration. These metrics serve as objective measures for evaluating controller effectiveness and guiding parameter tuning processes. The damping ratio and natural frequency, extracted from the characteristic equation, provide valuable insights into the system's dynamic behavior.
Frequency domain analysis complements time-domain stability assessments by offering additional performance metrics. Gain margin and phase margin, determined through Bode plot analysis, indicate the system's robustness against parameter variations and disturbances. A well-designed PID controller typically aims for a phase margin between 30° and 60° to balance performance with stability considerations.
Sensitivity analysis examines how variations in plant parameters affect closed-loop stability and performance. The sensitivity function, derived from the Laplace domain transfer function, quantifies the system's susceptibility to disturbances and modeling uncertainties. Lower sensitivity magnitudes across operational frequencies indicate superior disturbance rejection capabilities, a desirable characteristic in industrial control applications.
Error analysis in the Laplace domain enables the evaluation of steady-state performance for different input types. The final value theorem facilitates the calculation of steady-state errors for step, ramp, and parabolic inputs. The integral of absolute error (IAE) and integral of time-weighted absolute error (ITAE) metrics, computed from the error transfer function, provide comprehensive measures of controller performance across the entire response duration.
Robustness analysis extends traditional stability assessments by considering the system's ability to maintain performance despite parameter variations. The structured singular value (μ-analysis) and H∞ norm, both computed in the Laplace domain, quantify robustness against specific uncertainty models. These advanced metrics have become increasingly important in modern control system design, particularly for safety-critical applications where performance must be guaranteed across varying operating conditions.
Performance metrics for PID control systems can be directly derived from the Laplace domain representation. The transient response characteristics—including rise time, settling time, and percentage overshoot—are quantifiable through the system's poles and zeros configuration. These metrics serve as objective measures for evaluating controller effectiveness and guiding parameter tuning processes. The damping ratio and natural frequency, extracted from the characteristic equation, provide valuable insights into the system's dynamic behavior.
Frequency domain analysis complements time-domain stability assessments by offering additional performance metrics. Gain margin and phase margin, determined through Bode plot analysis, indicate the system's robustness against parameter variations and disturbances. A well-designed PID controller typically aims for a phase margin between 30° and 60° to balance performance with stability considerations.
Sensitivity analysis examines how variations in plant parameters affect closed-loop stability and performance. The sensitivity function, derived from the Laplace domain transfer function, quantifies the system's susceptibility to disturbances and modeling uncertainties. Lower sensitivity magnitudes across operational frequencies indicate superior disturbance rejection capabilities, a desirable characteristic in industrial control applications.
Error analysis in the Laplace domain enables the evaluation of steady-state performance for different input types. The final value theorem facilitates the calculation of steady-state errors for step, ramp, and parabolic inputs. The integral of absolute error (IAE) and integral of time-weighted absolute error (ITAE) metrics, computed from the error transfer function, provide comprehensive measures of controller performance across the entire response duration.
Robustness analysis extends traditional stability assessments by considering the system's ability to maintain performance despite parameter variations. The structured singular value (μ-analysis) and H∞ norm, both computed in the Laplace domain, quantify robustness against specific uncertainty models. These advanced metrics have become increasingly important in modern control system design, particularly for safety-critical applications where performance must be guaranteed across varying operating conditions.
Real-time Implementation Challenges and Solutions
Implementing PID controllers in real-time systems presents significant challenges that engineers must address to ensure optimal performance. The transition from theoretical Laplace domain analysis to practical implementation requires careful consideration of computational limitations. Most embedded systems operate with finite processing power and memory, creating constraints on the complexity of control algorithms. The discretization of continuous-time PID equations introduces approximation errors that can affect system stability, particularly when dealing with high-frequency dynamics or systems requiring precise timing.
Sampling rate selection represents a critical implementation challenge. According to control theory principles, the sampling frequency should be at least 10 times faster than the system's bandwidth to maintain adequate performance. However, hardware limitations often force compromises, requiring engineers to balance control accuracy against computational efficiency. Insufficient sampling rates can lead to aliasing effects and degraded control performance, while excessive rates may overwhelm available processing resources.
Numerical precision issues further complicate real-time implementation. Fixed-point arithmetic, commonly used in resource-constrained embedded systems, introduces quantization errors that can accumulate over time. These errors potentially destabilize control loops, especially in systems with integral components where error accumulation is inherent. Modern solutions include careful scaling of control parameters and implementing anti-windup mechanisms to prevent integral term saturation.
Communication delays present another significant challenge in distributed control systems. Network latency, particularly in wireless implementations, introduces time-varying delays that can destabilize PID controllers designed using Laplace domain analysis. Advanced techniques such as Smith predictors and delay-compensating algorithms have emerged to mitigate these effects, allowing for more robust performance in networked control applications.
Hardware limitations often necessitate code optimization strategies. Techniques such as lookup tables for complex calculations, efficient interrupt handling, and specialized DSP instructions can significantly improve execution speed. Many modern microcontrollers include dedicated peripheral modules for PWM generation, ADC sampling, and timer management, which can offload computational burden from the main processor when properly utilized.
Testing and validation methodologies have evolved to address these implementation challenges. Hardware-in-the-loop simulation allows engineers to verify controller performance under realistic conditions before deployment. Automated code generation tools have also emerged, translating Laplace domain designs directly into optimized embedded code while maintaining traceability between theoretical models and implementation.
Sampling rate selection represents a critical implementation challenge. According to control theory principles, the sampling frequency should be at least 10 times faster than the system's bandwidth to maintain adequate performance. However, hardware limitations often force compromises, requiring engineers to balance control accuracy against computational efficiency. Insufficient sampling rates can lead to aliasing effects and degraded control performance, while excessive rates may overwhelm available processing resources.
Numerical precision issues further complicate real-time implementation. Fixed-point arithmetic, commonly used in resource-constrained embedded systems, introduces quantization errors that can accumulate over time. These errors potentially destabilize control loops, especially in systems with integral components where error accumulation is inherent. Modern solutions include careful scaling of control parameters and implementing anti-windup mechanisms to prevent integral term saturation.
Communication delays present another significant challenge in distributed control systems. Network latency, particularly in wireless implementations, introduces time-varying delays that can destabilize PID controllers designed using Laplace domain analysis. Advanced techniques such as Smith predictors and delay-compensating algorithms have emerged to mitigate these effects, allowing for more robust performance in networked control applications.
Hardware limitations often necessitate code optimization strategies. Techniques such as lookup tables for complex calculations, efficient interrupt handling, and specialized DSP instructions can significantly improve execution speed. Many modern microcontrollers include dedicated peripheral modules for PWM generation, ADC sampling, and timer management, which can offload computational burden from the main processor when properly utilized.
Testing and validation methodologies have evolved to address these implementation challenges. Hardware-in-the-loop simulation allows engineers to verify controller performance under realistic conditions before deployment. Automated code generation tools have also emerged, translating Laplace domain designs directly into optimized embedded code while maintaining traceability between theoretical models and implementation.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!