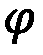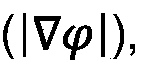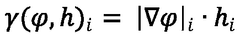Topology Optimization for Custom Tool Design: Optimization Techniques
SEP 16, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Topology Optimization Background and Objectives
Topology optimization has emerged as a transformative approach in engineering design, evolving from theoretical concepts in the 1980s to a practical design methodology widely adopted across industries today. This mathematical method determines the optimal material distribution within a given design space, subject to specified constraints and performance criteria, ultimately creating structures that maximize performance while minimizing material usage. The fundamental principle behind topology optimization is to identify where material is most needed within a design domain to achieve desired functional requirements.
The evolution of topology optimization has been closely tied to advancements in computational capabilities. Early implementations were limited to simple 2D problems with basic loading conditions, but modern algorithms can handle complex 3D geometries with multiple load cases, manufacturing constraints, and multiphysics considerations. The development of the Solid Isotropic Material with Penalization (SIMP) method in the 1990s marked a significant milestone, providing a practical framework for implementing topology optimization in commercial software.
For custom tool design specifically, topology optimization represents a paradigm shift from traditional design approaches based on intuition and experience to data-driven, performance-oriented methodologies. Tools designed using topology optimization can achieve superior strength-to-weight ratios, improved ergonomics, and enhanced functional performance while using less material. This is particularly valuable in industries where tool weight, durability, and specialized functionality directly impact productivity and user experience.
The primary objective of topology optimization in custom tool design is to create tools that perfectly balance multiple competing requirements: structural integrity, weight reduction, manufacturability, and application-specific performance metrics. Secondary objectives often include minimizing production costs, reducing material waste, and improving sustainability profiles of the resulting products.
Current research trends in this field focus on integrating additive manufacturing capabilities with topology optimization algorithms, as 3D printing technologies can fabricate the complex geometries that often result from optimization processes. Additionally, there is growing interest in incorporating user-centered design principles into the optimization workflow, ensuring that the mathematically optimal solutions also address human factors and ergonomic considerations.
Looking forward, the trajectory of topology optimization for custom tool design points toward more accessible implementation, with algorithms becoming increasingly sophisticated yet user-friendly. The integration of machine learning approaches to predict optimal starting points for optimization and the development of real-time optimization capabilities represent frontier areas that promise to further revolutionize custom tool design methodologies.
The evolution of topology optimization has been closely tied to advancements in computational capabilities. Early implementations were limited to simple 2D problems with basic loading conditions, but modern algorithms can handle complex 3D geometries with multiple load cases, manufacturing constraints, and multiphysics considerations. The development of the Solid Isotropic Material with Penalization (SIMP) method in the 1990s marked a significant milestone, providing a practical framework for implementing topology optimization in commercial software.
For custom tool design specifically, topology optimization represents a paradigm shift from traditional design approaches based on intuition and experience to data-driven, performance-oriented methodologies. Tools designed using topology optimization can achieve superior strength-to-weight ratios, improved ergonomics, and enhanced functional performance while using less material. This is particularly valuable in industries where tool weight, durability, and specialized functionality directly impact productivity and user experience.
The primary objective of topology optimization in custom tool design is to create tools that perfectly balance multiple competing requirements: structural integrity, weight reduction, manufacturability, and application-specific performance metrics. Secondary objectives often include minimizing production costs, reducing material waste, and improving sustainability profiles of the resulting products.
Current research trends in this field focus on integrating additive manufacturing capabilities with topology optimization algorithms, as 3D printing technologies can fabricate the complex geometries that often result from optimization processes. Additionally, there is growing interest in incorporating user-centered design principles into the optimization workflow, ensuring that the mathematically optimal solutions also address human factors and ergonomic considerations.
Looking forward, the trajectory of topology optimization for custom tool design points toward more accessible implementation, with algorithms becoming increasingly sophisticated yet user-friendly. The integration of machine learning approaches to predict optimal starting points for optimization and the development of real-time optimization capabilities represent frontier areas that promise to further revolutionize custom tool design methodologies.
Market Demand for Custom Tool Design Solutions
The market for custom tool design solutions utilizing topology optimization is experiencing significant growth, driven by the increasing demand for lightweight, high-performance components across multiple industries. Manufacturing sectors, particularly aerospace, automotive, and medical device industries, are actively seeking advanced optimization techniques to reduce material usage while maintaining or enhancing structural integrity and performance characteristics.
Recent market analyses indicate that the global topology optimization software market is expanding at a compound annual growth rate of approximately 15%, with particular acceleration in regions with strong manufacturing bases such as North America, Western Europe, and East Asia. This growth is primarily fueled by the need to reduce production costs and material waste while meeting increasingly stringent performance requirements.
The automotive industry represents one of the largest market segments, where lightweighting initiatives are critical for improving fuel efficiency and meeting emissions regulations. Aerospace manufacturers similarly require topology-optimized tools and components to reduce aircraft weight without compromising safety or durability. The medical device sector shows rapidly growing demand for customized surgical instruments and implants that can be precisely tailored to patient anatomy.
Market research reveals that companies are increasingly willing to invest in advanced design solutions that can demonstrate clear return on investment through material savings, reduced development cycles, and improved product performance. The average material savings achieved through topology optimization ranges between 30-50%, representing substantial cost reductions in high-volume manufacturing operations.
Small and medium enterprises (SMEs) are emerging as a significant growth segment, as more affordable and user-friendly topology optimization solutions become available. These businesses seek tools that can be integrated into existing design workflows without requiring extensive specialized training or computational resources.
Customer feedback indicates growing demand for topology optimization solutions that can address multi-physics problems, incorporating thermal, fluid, and electromagnetic considerations alongside structural optimization. There is also increasing interest in solutions that can optimize for manufacturing constraints specific to different production methods, including traditional machining, additive manufacturing, and injection molding.
The market shows clear preference for solutions offering seamless integration with existing CAD/CAM systems, intuitive user interfaces, and the ability to quickly iterate through design alternatives. Cloud-based solutions are gaining traction, particularly among organizations with distributed design teams or those seeking to reduce infrastructure costs.
Recent market analyses indicate that the global topology optimization software market is expanding at a compound annual growth rate of approximately 15%, with particular acceleration in regions with strong manufacturing bases such as North America, Western Europe, and East Asia. This growth is primarily fueled by the need to reduce production costs and material waste while meeting increasingly stringent performance requirements.
The automotive industry represents one of the largest market segments, where lightweighting initiatives are critical for improving fuel efficiency and meeting emissions regulations. Aerospace manufacturers similarly require topology-optimized tools and components to reduce aircraft weight without compromising safety or durability. The medical device sector shows rapidly growing demand for customized surgical instruments and implants that can be precisely tailored to patient anatomy.
Market research reveals that companies are increasingly willing to invest in advanced design solutions that can demonstrate clear return on investment through material savings, reduced development cycles, and improved product performance. The average material savings achieved through topology optimization ranges between 30-50%, representing substantial cost reductions in high-volume manufacturing operations.
Small and medium enterprises (SMEs) are emerging as a significant growth segment, as more affordable and user-friendly topology optimization solutions become available. These businesses seek tools that can be integrated into existing design workflows without requiring extensive specialized training or computational resources.
Customer feedback indicates growing demand for topology optimization solutions that can address multi-physics problems, incorporating thermal, fluid, and electromagnetic considerations alongside structural optimization. There is also increasing interest in solutions that can optimize for manufacturing constraints specific to different production methods, including traditional machining, additive manufacturing, and injection molding.
The market shows clear preference for solutions offering seamless integration with existing CAD/CAM systems, intuitive user interfaces, and the ability to quickly iterate through design alternatives. Cloud-based solutions are gaining traction, particularly among organizations with distributed design teams or those seeking to reduce infrastructure costs.
Current Topology Optimization Challenges
Despite significant advancements in topology optimization for custom tool design, several critical challenges persist that impede broader industrial adoption and limit optimization effectiveness. Computational complexity remains a primary obstacle, with high-fidelity simulations requiring substantial processing power and time, especially for complex 3D geometries with multiple loading conditions. This computational burden often forces engineers to compromise between solution accuracy and practical timeframes, resulting in suboptimal designs or excessive iteration cycles.
Manufacturing constraints present another significant challenge, as theoretically optimal designs frequently include complex geometries that prove difficult or impossible to fabricate using conventional manufacturing methods. While additive manufacturing has alleviated some constraints, the disconnect between optimization algorithms and manufacturing realities continues to produce designs requiring substantial post-optimization modification, diminishing the benefits of the optimization process.
Multi-physics considerations further complicate topology optimization for tools. Most current algorithms excel at addressing single-physics problems (typically structural mechanics), but tools often operate in environments involving thermal loads, fluid interactions, and dynamic conditions. Integrating these diverse physics domains into a unified optimization framework remains technically challenging, leading to oversimplified models that may not perform as expected in real-world applications.
Material nonlinearity and anisotropy represent additional hurdles. Many topology optimization algorithms assume linear elastic material behavior, whereas actual tool materials exhibit nonlinear responses, particularly under extreme conditions. Similarly, advanced materials with directional properties (composites, additively manufactured structures) require specialized optimization approaches that are not yet fully mature.
Uncertainty quantification and robust design optimization remain underdeveloped areas. Real-world tools operate under variable and uncertain conditions, yet most topology optimization frameworks lack robust mechanisms to account for these uncertainties, potentially leading to designs that perform well under nominal conditions but fail when subjected to variations in loading, material properties, or environmental factors.
Integration with existing design workflows presents practical implementation challenges. Current topology optimization tools often exist as standalone solutions rather than seamlessly integrating with CAD systems and PLM platforms. This integration gap creates friction in the design process, requiring manual intervention and interpretation between optimization results and final design specifications.
Manufacturing constraints present another significant challenge, as theoretically optimal designs frequently include complex geometries that prove difficult or impossible to fabricate using conventional manufacturing methods. While additive manufacturing has alleviated some constraints, the disconnect between optimization algorithms and manufacturing realities continues to produce designs requiring substantial post-optimization modification, diminishing the benefits of the optimization process.
Multi-physics considerations further complicate topology optimization for tools. Most current algorithms excel at addressing single-physics problems (typically structural mechanics), but tools often operate in environments involving thermal loads, fluid interactions, and dynamic conditions. Integrating these diverse physics domains into a unified optimization framework remains technically challenging, leading to oversimplified models that may not perform as expected in real-world applications.
Material nonlinearity and anisotropy represent additional hurdles. Many topology optimization algorithms assume linear elastic material behavior, whereas actual tool materials exhibit nonlinear responses, particularly under extreme conditions. Similarly, advanced materials with directional properties (composites, additively manufactured structures) require specialized optimization approaches that are not yet fully mature.
Uncertainty quantification and robust design optimization remain underdeveloped areas. Real-world tools operate under variable and uncertain conditions, yet most topology optimization frameworks lack robust mechanisms to account for these uncertainties, potentially leading to designs that perform well under nominal conditions but fail when subjected to variations in loading, material properties, or environmental factors.
Integration with existing design workflows presents practical implementation challenges. Current topology optimization tools often exist as standalone solutions rather than seamlessly integrating with CAD systems and PLM platforms. This integration gap creates friction in the design process, requiring manual intervention and interpretation between optimization results and final design specifications.
Current Optimization Algorithms and Approaches
01 Evolutionary and genetic algorithms for topology optimization
Evolutionary and genetic algorithms are used in topology optimization to efficiently search large design spaces. These algorithms mimic natural selection processes to iteratively improve designs by evaluating fitness functions, selecting promising candidates, and applying operations like crossover and mutation. This approach is particularly effective for complex structural optimization problems where traditional gradient-based methods may struggle, allowing for exploration of novel design solutions while handling multiple objectives and constraints.- Evolutionary and genetic algorithms for topology optimization: Evolutionary and genetic algorithms are employed in topology optimization to efficiently search large design spaces. These algorithms mimic natural selection processes by iteratively improving design solutions through operations like mutation, crossover, and selection. They are particularly effective for complex structural optimization problems where traditional gradient-based methods may struggle, allowing for exploration of non-intuitive design solutions while handling multiple objectives and constraints simultaneously.
- Machine learning approaches in topology optimization: Machine learning techniques are increasingly applied to topology optimization to accelerate the design process and improve results. These approaches use neural networks, deep learning, and other AI methods to predict optimal designs based on training data from previous optimization runs. Machine learning can significantly reduce computational costs by approximating complex simulations, enabling real-time optimization feedback, and identifying patterns in successful designs that might not be apparent through conventional methods.
- Multi-objective and constraint handling techniques: Advanced methods for handling multiple objectives and constraints are essential in practical topology optimization problems. These techniques enable designers to simultaneously optimize for competing goals such as minimizing weight while maximizing stiffness, or meeting specific performance requirements while adhering to manufacturing constraints. Approaches include weighted sum methods, Pareto optimization, penalty functions, and specialized algorithms that can efficiently navigate complex design spaces with multiple constraints.
- Gradient-based optimization methods: Gradient-based methods form the foundation of many topology optimization approaches, using sensitivity analysis to efficiently navigate design spaces. These techniques calculate how design changes affect performance metrics, allowing for systematic improvement through iterative updates. Methods such as SIMP (Solid Isotropic Material with Penalization), level set methods, and adjoint sensitivity analysis enable efficient optimization of complex structures by following the steepest improvement path while managing computational resources effectively.
- Integration with manufacturing constraints and processes: Topology optimization techniques that incorporate manufacturing constraints ensure that optimized designs can be practically produced. These methods consider specific manufacturing processes like additive manufacturing, casting, or machining during the optimization process rather than as post-processing steps. By embedding constraints such as minimum feature size, overhang angles, or material anisotropy directly into the optimization algorithm, these approaches produce designs that are both high-performing and manufacturable without significant redesign.
02 Machine learning and AI-based topology optimization techniques
Machine learning and artificial intelligence approaches are increasingly applied to topology optimization problems. These techniques leverage neural networks, deep learning, and reinforcement learning to predict optimal designs, accelerate convergence, and reduce computational costs. By training on existing optimization results, these methods can quickly generate near-optimal solutions for new design problems, enabling real-time optimization and handling of complex multi-physics constraints that traditional methods find challenging.Expand Specific Solutions03 Multi-objective and constraint-based optimization methods
Multi-objective optimization techniques allow for simultaneous consideration of multiple design goals in topology optimization. These methods employ Pareto optimization, weighted sum approaches, and constraint handling techniques to balance competing objectives such as weight reduction, structural strength, thermal performance, and manufacturing constraints. Advanced formulations incorporate both explicit and implicit constraints to ensure designs meet practical requirements while maintaining optimal performance across multiple criteria.Expand Specific Solutions04 Level set and density-based topology optimization
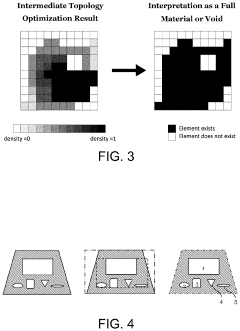
Level set and density-based methods represent two fundamental approaches to topology optimization. Level set methods define structural boundaries using implicit functions, allowing for smooth boundary representation and natural handling of topological changes. Density-based methods, including SIMP (Solid Isotropic Material with Penalization), assign material density values to each element in the design space. Both approaches offer different advantages in terms of boundary representation, computational efficiency, and manufacturing constraints implementation.Expand Specific Solutions05 Integration with additive manufacturing and computational efficiency
Modern topology optimization techniques are increasingly integrated with additive manufacturing constraints and focused on computational efficiency. These methods incorporate manufacturing-specific constraints such as minimum feature size, support structure requirements, and build orientation directly into the optimization process. Parallel computing, model order reduction, and adaptive mesh refinement techniques are employed to reduce computational costs while maintaining solution accuracy, enabling optimization of larger and more complex structures.Expand Specific Solutions
Leading Players in Topology Optimization Software
Topology optimization for custom tool design is currently in a growth phase, with the market expanding due to increasing demand for lightweight, high-performance components across industries. The global market size is estimated to reach significant value as manufacturers seek efficiency improvements through optimized designs. Technologically, the field is maturing rapidly with companies like Siemens AG, Autodesk, and Dassault Systèmes leading commercial implementation through advanced simulation software. ANSYS and Siemens offer comprehensive topology optimization solutions integrated with manufacturing constraints, while academic institutions like MIT, Georgia Tech, and University of Michigan contribute fundamental research advancing algorithmic approaches. The competitive landscape shows software providers expanding capabilities while manufacturers increasingly adopt these technologies for production advantages.
Siemens AG
Technical Solution: Siemens has developed advanced topology optimization solutions through their NX and Simcenter software suites. Their approach integrates multi-physics simulation with generative design capabilities to create optimized tool designs based on specified constraints and performance requirements. The technology employs non-parametric optimization algorithms that can handle complex design spaces while considering manufacturing constraints such as minimum member size, symmetry requirements, and casting/machining limitations[1]. Siemens' methodology incorporates both SIMP (Solid Isotropic Material with Penalization) and level-set methods, allowing engineers to define design spaces, loading conditions, and optimization objectives while the system iteratively removes material from low-stress regions. Their platform also features advanced smoothing algorithms that convert the optimized topology into manufacturable CAD models, reducing post-processing requirements[3]. Recent developments include integration of machine learning techniques to accelerate convergence and improve solution quality based on historical optimization data.
Strengths: Comprehensive integration with manufacturing workflows; robust multi-physics capabilities; advanced smoothing algorithms for CAD conversion. Weaknesses: Computationally intensive for complex problems; requires significant expertise to set up optimization parameters effectively; sometimes produces designs requiring substantial interpretation and manual refinement.
Autodesk, Inc.
Technical Solution: Autodesk has pioneered generative design approaches to topology optimization through their Fusion 360 platform. Their technology utilizes cloud-based computing resources to explore thousands of design alternatives simultaneously based on specified constraints, loads, and manufacturing methods. The system employs both traditional density-based topology optimization and more advanced lattice optimization techniques that create lightweight structures with tailored mechanical properties[2]. Autodesk's approach is distinctive in its use of evolutionary algorithms alongside gradient-based methods, allowing exploration of non-convex design spaces and discrete material choices. Their platform incorporates manufacturing constraints directly into the optimization process, including considerations for 3D printing, CNC machining, and casting processes[4]. Recent enhancements include thermal and fluid flow considerations in the optimization workflow, enabling multi-physics optimization for tools operating in complex thermal environments. The system also features automated interpretation of optimization results into parametric CAD models with feature recognition capabilities.
Strengths: Intuitive user interface accessible to non-specialists; cloud computing resources enable rapid exploration of design alternatives; excellent integration with manufacturing constraints. Weaknesses: Subscription-based pricing can be costly for smaller organizations; limited customization of optimization algorithms; occasional challenges with complex load case definitions.
Key Technical Innovations in Constraint Handling
Topology optimization with bidirectional mesh adaptation
PatentWO2023133734A1
Innovation
- Bidirectional mesh adaptation technique that dynamically adjusts mesh resolution during topology optimization, allowing for both refinement and coarsening based on optimization progress.
- Multi-physics topology optimization approach that balances computational efficiency with design detail preservation, particularly for thermal-flow applications like gas turbine components.
- Mesh-sensitive topology optimization method that maintains accuracy while reducing computational resources through strategic mesh distribution.
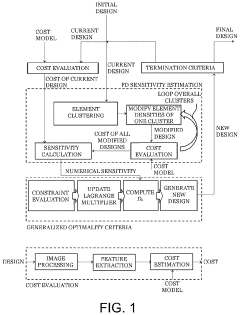
Method for structural optimization of a design and cost of a physical object
PatentActiveUS20230196290A1
Innovation
- A computer-implemented method that uses element clustering and numerical estimation to optimize material density distribution, integrating manufacturing costs as an objective function within the topology optimization algorithm, allowing for iterative material density adjustments based on analytical and numerical derivatives to minimize manufacturing costs while maintaining structural performance.
Manufacturing Constraints and Practical Implementation
The implementation of topology optimization in custom tool design requires careful consideration of manufacturing constraints to ensure that optimized designs can be practically produced. Traditional manufacturing methods often impose limitations on what can be physically fabricated, creating a gap between theoretically optimal designs and manufacturable solutions.
Additive manufacturing technologies, particularly metal 3D printing, have significantly expanded the feasible design space for topology-optimized tools. However, even these advanced processes have constraints that must be incorporated into the optimization algorithm. Minimum feature size represents a critical constraint, as structures below certain dimensions cannot be reliably manufactured. For metal powder bed fusion processes, features typically need to exceed 0.5mm to ensure structural integrity.
Overhang angles present another significant manufacturing challenge. Structures with angles exceeding 45 degrees from vertical often require support structures, which can be difficult to remove from internal cavities of custom tools. Build orientation must be strategically determined to minimize support requirements while maintaining optimal mechanical properties in critical tool regions.
Surface finish considerations directly impact tool functionality, particularly for cutting tools where edge quality determines performance. Post-processing operations such as machining or polishing must be factored into the design phase, with sufficient material allowance incorporated into the optimization model.
Material anisotropy resulting from layer-by-layer manufacturing processes creates directionally dependent mechanical properties. This phenomenon must be accounted for in the optimization algorithm to ensure that critical load paths align with directions of maximum material strength.
Cost-effective implementation requires balancing performance gains against manufacturing complexity. Hybrid manufacturing approaches combining additive techniques for complex geometries with traditional machining for precision surfaces often yield the most practical results. This approach necessitates design for hybrid manufacturing principles, including appropriate datum features and machining allowances.
Validation protocols through physical testing remain essential, as simulation models may not fully capture all manufacturing-induced variations. Iterative prototyping with progressive refinement based on performance testing has proven effective for implementing topology-optimized tools in production environments.
Industry case studies demonstrate that successful implementation typically involves close collaboration between design engineers, manufacturing specialists, and end-users to navigate the complex trade-offs between theoretical optimization and practical manufacturing constraints.
Additive manufacturing technologies, particularly metal 3D printing, have significantly expanded the feasible design space for topology-optimized tools. However, even these advanced processes have constraints that must be incorporated into the optimization algorithm. Minimum feature size represents a critical constraint, as structures below certain dimensions cannot be reliably manufactured. For metal powder bed fusion processes, features typically need to exceed 0.5mm to ensure structural integrity.
Overhang angles present another significant manufacturing challenge. Structures with angles exceeding 45 degrees from vertical often require support structures, which can be difficult to remove from internal cavities of custom tools. Build orientation must be strategically determined to minimize support requirements while maintaining optimal mechanical properties in critical tool regions.
Surface finish considerations directly impact tool functionality, particularly for cutting tools where edge quality determines performance. Post-processing operations such as machining or polishing must be factored into the design phase, with sufficient material allowance incorporated into the optimization model.
Material anisotropy resulting from layer-by-layer manufacturing processes creates directionally dependent mechanical properties. This phenomenon must be accounted for in the optimization algorithm to ensure that critical load paths align with directions of maximum material strength.
Cost-effective implementation requires balancing performance gains against manufacturing complexity. Hybrid manufacturing approaches combining additive techniques for complex geometries with traditional machining for precision surfaces often yield the most practical results. This approach necessitates design for hybrid manufacturing principles, including appropriate datum features and machining allowances.
Validation protocols through physical testing remain essential, as simulation models may not fully capture all manufacturing-induced variations. Iterative prototyping with progressive refinement based on performance testing has proven effective for implementing topology-optimized tools in production environments.
Industry case studies demonstrate that successful implementation typically involves close collaboration between design engineers, manufacturing specialists, and end-users to navigate the complex trade-offs between theoretical optimization and practical manufacturing constraints.
Material Selection Impact on Optimization Results
Material selection represents a critical factor in topology optimization processes for custom tool design, significantly influencing both the optimization outcomes and the practical performance of the resulting tools. Different materials exhibit unique combinations of mechanical properties, including elastic modulus, yield strength, density, and thermal characteristics, which directly affect the optimization algorithm's solution space and constraints. When implementing topology optimization for custom tools, engineers must carefully consider how material properties interact with the optimization objectives, as this relationship fundamentally shapes the final design geometry.
The selection of materials creates distinct boundaries for optimization possibilities. For instance, high-strength alloys permit designs with thinner structural elements while maintaining required load-bearing capabilities, whereas more ductile materials may necessitate additional material volume to achieve equivalent performance. This relationship becomes particularly evident in multi-material optimization scenarios, where the algorithm must simultaneously determine both the optimal geometry and the optimal material distribution throughout the structure.
Computational models must accurately incorporate material-specific parameters to generate realistic optimization results. Material isotropy versus anisotropy significantly impacts the optimization process, with anisotropic materials (like fiber-reinforced composites) requiring more sophisticated modeling approaches that account for directional property variations. The optimization algorithm must integrate these complex material behaviors to produce manufacturable designs that perform as intended under operational conditions.
Manufacturing constraints associated with specific materials further influence optimization outcomes. Additive manufacturing processes, increasingly common for producing topology-optimized tools, impose material-dependent limitations regarding minimum feature size, support structures, and build orientation. Materials with poor thermal conductivity may experience greater residual stresses during fabrication, potentially compromising the structural integrity predicted by the optimization model.
Cost considerations related to material selection also play a decisive role in practical optimization implementations. Premium materials with superior mechanical properties might enable more efficient designs with reduced material volume, but their higher cost may offset these advantages in commercial applications. Consequently, effective topology optimization must balance material performance characteristics against economic constraints, often requiring multi-objective optimization approaches that simultaneously consider structural performance, material utilization, and production costs.
Recent research demonstrates that incorporating material selection as an active variable within the optimization process, rather than a predetermined constraint, can yield superior results in custom tool design. This approach, known as concurrent material and topology optimization, represents an emerging frontier in the field, enabling more comprehensive exploration of the design space and potentially revolutionary tool designs that maximize performance while minimizing resource utilization.
The selection of materials creates distinct boundaries for optimization possibilities. For instance, high-strength alloys permit designs with thinner structural elements while maintaining required load-bearing capabilities, whereas more ductile materials may necessitate additional material volume to achieve equivalent performance. This relationship becomes particularly evident in multi-material optimization scenarios, where the algorithm must simultaneously determine both the optimal geometry and the optimal material distribution throughout the structure.
Computational models must accurately incorporate material-specific parameters to generate realistic optimization results. Material isotropy versus anisotropy significantly impacts the optimization process, with anisotropic materials (like fiber-reinforced composites) requiring more sophisticated modeling approaches that account for directional property variations. The optimization algorithm must integrate these complex material behaviors to produce manufacturable designs that perform as intended under operational conditions.
Manufacturing constraints associated with specific materials further influence optimization outcomes. Additive manufacturing processes, increasingly common for producing topology-optimized tools, impose material-dependent limitations regarding minimum feature size, support structures, and build orientation. Materials with poor thermal conductivity may experience greater residual stresses during fabrication, potentially compromising the structural integrity predicted by the optimization model.
Cost considerations related to material selection also play a decisive role in practical optimization implementations. Premium materials with superior mechanical properties might enable more efficient designs with reduced material volume, but their higher cost may offset these advantages in commercial applications. Consequently, effective topology optimization must balance material performance characteristics against economic constraints, often requiring multi-objective optimization approaches that simultaneously consider structural performance, material utilization, and production costs.
Recent research demonstrates that incorporating material selection as an active variable within the optimization process, rather than a predetermined constraint, can yield superior results in custom tool design. This approach, known as concurrent material and topology optimization, represents an emerging frontier in the field, enabling more comprehensive exploration of the design space and potentially revolutionary tool designs that maximize performance while minimizing resource utilization.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!