Error Propagation Analysis In Approximate In-Memory Computing
SEP 2, 20259 MIN READ
Generate Your Research Report Instantly with AI Agent
Patsnap Eureka helps you evaluate technical feasibility & market potential.
Error Propagation Background and Objectives
Approximate In-Memory Computing (AIMC) has emerged as a promising paradigm to address the growing computational demands and energy constraints in modern computing systems. This technology integrates computation directly within memory units, eliminating the costly data movement between processing and storage components that dominates energy consumption in conventional von Neumann architectures. The concept of AIMC has evolved significantly over the past decade, transitioning from theoretical frameworks to practical implementations across various memory technologies including SRAM, DRAM, and emerging non-volatile memories.
Error propagation in AIMC represents a critical challenge that has gained increasing attention as these systems move toward commercial viability. The inherent nature of approximate computing introduces computational errors that can propagate through complex processing chains, potentially compromising output quality and system reliability. Understanding these error mechanisms is essential for developing robust AIMC architectures that can deliver meaningful computational advantages while maintaining acceptable accuracy levels.
The technical evolution in this domain has been characterized by progressive improvements in error mitigation strategies, from basic error compensation techniques to sophisticated error-aware design methodologies. Recent advancements have focused on developing mathematical models that can accurately predict error propagation patterns across different computational layers, enabling more effective system optimization and quality control.
The primary objective of error propagation analysis in AIMC is to establish comprehensive theoretical frameworks and practical methodologies for characterizing, predicting, and controlling computational errors throughout the processing pipeline. This includes developing accurate error models that account for various error sources such as device variations, quantization effects, and algorithmic approximations, as well as their cumulative impact on final computation results.
Additionally, this analysis aims to establish quality-energy tradeoff metrics that can guide system designers in optimizing AIMC implementations for specific application requirements. By understanding how errors propagate and affect different applications, designers can make informed decisions about acceptable error thresholds and appropriate error mitigation techniques.
Long-term technical goals include developing adaptive error management systems that can dynamically adjust computational precision based on application needs and energy constraints. This would enable AIMC systems to intelligently balance accuracy and efficiency across diverse workloads, maximizing the benefits of approximate computing while ensuring reliable operation.
The evolution of error propagation analysis is expected to play a pivotal role in advancing AIMC technology from specialized accelerators to mainstream computing solutions, potentially revolutionizing the energy efficiency and performance of next-generation computing systems across various domains including edge computing, artificial intelligence, and high-performance computing.
Error propagation in AIMC represents a critical challenge that has gained increasing attention as these systems move toward commercial viability. The inherent nature of approximate computing introduces computational errors that can propagate through complex processing chains, potentially compromising output quality and system reliability. Understanding these error mechanisms is essential for developing robust AIMC architectures that can deliver meaningful computational advantages while maintaining acceptable accuracy levels.
The technical evolution in this domain has been characterized by progressive improvements in error mitigation strategies, from basic error compensation techniques to sophisticated error-aware design methodologies. Recent advancements have focused on developing mathematical models that can accurately predict error propagation patterns across different computational layers, enabling more effective system optimization and quality control.
The primary objective of error propagation analysis in AIMC is to establish comprehensive theoretical frameworks and practical methodologies for characterizing, predicting, and controlling computational errors throughout the processing pipeline. This includes developing accurate error models that account for various error sources such as device variations, quantization effects, and algorithmic approximations, as well as their cumulative impact on final computation results.
Additionally, this analysis aims to establish quality-energy tradeoff metrics that can guide system designers in optimizing AIMC implementations for specific application requirements. By understanding how errors propagate and affect different applications, designers can make informed decisions about acceptable error thresholds and appropriate error mitigation techniques.
Long-term technical goals include developing adaptive error management systems that can dynamically adjust computational precision based on application needs and energy constraints. This would enable AIMC systems to intelligently balance accuracy and efficiency across diverse workloads, maximizing the benefits of approximate computing while ensuring reliable operation.
The evolution of error propagation analysis is expected to play a pivotal role in advancing AIMC technology from specialized accelerators to mainstream computing solutions, potentially revolutionizing the energy efficiency and performance of next-generation computing systems across various domains including edge computing, artificial intelligence, and high-performance computing.
Market Demand for Approximate Computing Solutions
The market for approximate computing solutions is experiencing significant growth driven by the increasing demands for energy-efficient computing in data-intensive applications. As traditional computing approaches face fundamental power and performance limitations, approximate computing has emerged as a promising paradigm that trades computational accuracy for substantial improvements in energy efficiency, performance, and hardware cost.
The global market for energy-efficient computing solutions is projected to reach $25.3 billion by 2025, with approximate computing representing a rapidly growing segment. This growth is primarily fueled by the exponential increase in data processing requirements across various industries, including artificial intelligence, machine learning, multimedia processing, and IoT applications.
In the AI and machine learning sector, which is expected to grow at a CAGR of 42.2% through 2027, approximate computing solutions are particularly valuable. These applications often demonstrate inherent error resilience, making them ideal candidates for approximation techniques that can deliver up to 90% energy savings with minimal impact on output quality.
The mobile and edge computing markets are also driving demand for approximate computing solutions. With over 75 billion IoT devices expected to be deployed by 2025, there is an urgent need for energy-efficient processing capabilities that can operate within strict power constraints. Approximate in-memory computing addresses this challenge by reducing data movement between memory and processing units, which typically accounts for 60-70% of total system energy consumption.
Data centers represent another significant market segment, with operators increasingly seeking solutions to manage escalating energy costs. Approximate computing techniques can reduce computational load for suitable workloads, potentially decreasing data center energy consumption by 15-20% for applicable tasks.
The automotive and industrial sectors are emerging markets for approximate computing, particularly for sensor data processing and real-time analytics. These applications often tolerate some degree of imprecision while requiring high throughput and energy efficiency, creating an ideal use case for approximate in-memory computing solutions.
Despite this promising market outlook, adoption barriers remain. These include concerns about error management, lack of standardized tools for error propagation analysis, and limited developer expertise in approximate computing paradigms. Organizations report that understanding error propagation effects is the primary technical challenge when implementing approximate computing solutions, highlighting the critical importance of advanced error propagation analysis techniques in approximate in-memory computing.
The global market for energy-efficient computing solutions is projected to reach $25.3 billion by 2025, with approximate computing representing a rapidly growing segment. This growth is primarily fueled by the exponential increase in data processing requirements across various industries, including artificial intelligence, machine learning, multimedia processing, and IoT applications.
In the AI and machine learning sector, which is expected to grow at a CAGR of 42.2% through 2027, approximate computing solutions are particularly valuable. These applications often demonstrate inherent error resilience, making them ideal candidates for approximation techniques that can deliver up to 90% energy savings with minimal impact on output quality.
The mobile and edge computing markets are also driving demand for approximate computing solutions. With over 75 billion IoT devices expected to be deployed by 2025, there is an urgent need for energy-efficient processing capabilities that can operate within strict power constraints. Approximate in-memory computing addresses this challenge by reducing data movement between memory and processing units, which typically accounts for 60-70% of total system energy consumption.
Data centers represent another significant market segment, with operators increasingly seeking solutions to manage escalating energy costs. Approximate computing techniques can reduce computational load for suitable workloads, potentially decreasing data center energy consumption by 15-20% for applicable tasks.
The automotive and industrial sectors are emerging markets for approximate computing, particularly for sensor data processing and real-time analytics. These applications often tolerate some degree of imprecision while requiring high throughput and energy efficiency, creating an ideal use case for approximate in-memory computing solutions.
Despite this promising market outlook, adoption barriers remain. These include concerns about error management, lack of standardized tools for error propagation analysis, and limited developer expertise in approximate computing paradigms. Organizations report that understanding error propagation effects is the primary technical challenge when implementing approximate computing solutions, highlighting the critical importance of advanced error propagation analysis techniques in approximate in-memory computing.
Technical Challenges in In-Memory Computing Error Analysis
In-memory computing (IMC) faces significant technical challenges in error analysis, primarily due to the inherent trade-off between computational efficiency and accuracy. The integration of processing capabilities directly within memory units introduces unique error sources that traditional computing architectures do not encounter. These errors propagate through computational pipelines in complex, often unpredictable patterns, making systematic analysis particularly challenging.
The fundamental challenge lies in characterizing error behavior in analog computing environments where deterministic precision gives way to probabilistic outcomes. Resistive memory devices, commonly used in IMC architectures, exhibit non-ideal characteristics including temporal variations, cycle-to-cycle inconsistencies, and device-to-device variations. These variations introduce computational errors that compound through multi-stage operations, creating cascading effects that are difficult to model mathematically.
Thermal noise presents another significant challenge, as it introduces random fluctuations in analog values stored within memory arrays. This stochastic behavior becomes particularly problematic in deep neural network implementations where small errors in early layers can amplify dramatically through subsequent operations. Current error models struggle to capture these temperature-dependent effects accurately across different operational conditions.
Quantization errors represent a third major challenge, occurring when continuous analog values must be discretized for digital interpretation or further processing. The limited precision of analog-to-digital converters creates inherent approximation errors that vary based on the signal characteristics and conversion parameters. These quantization effects interact with other error sources in ways that resist straightforward analytical treatment.
The lack of standardized benchmarks for error analysis further complicates the field. Unlike digital computing, where error metrics are well-established, approximate in-memory computing lacks consensus on appropriate error tolerance thresholds for different applications. This absence of standardization makes comparative analysis between different IMC approaches particularly difficult.
Cross-layer error propagation presents perhaps the most complex challenge. Errors originating at the device level propagate through circuit, architecture, algorithm, and application layers, with each layer potentially amplifying, attenuating, or transforming error characteristics. Developing comprehensive models that span these abstraction levels requires interdisciplinary expertise that bridges material science, circuit design, computer architecture, and application-specific knowledge.
Finally, the dynamic nature of many IMC applications, particularly in edge computing scenarios, introduces temporal dependencies in error behavior. Workload variations, environmental changes, and aging effects create time-varying error profiles that static analysis methods cannot adequately capture, necessitating adaptive error monitoring and compensation techniques.
The fundamental challenge lies in characterizing error behavior in analog computing environments where deterministic precision gives way to probabilistic outcomes. Resistive memory devices, commonly used in IMC architectures, exhibit non-ideal characteristics including temporal variations, cycle-to-cycle inconsistencies, and device-to-device variations. These variations introduce computational errors that compound through multi-stage operations, creating cascading effects that are difficult to model mathematically.
Thermal noise presents another significant challenge, as it introduces random fluctuations in analog values stored within memory arrays. This stochastic behavior becomes particularly problematic in deep neural network implementations where small errors in early layers can amplify dramatically through subsequent operations. Current error models struggle to capture these temperature-dependent effects accurately across different operational conditions.
Quantization errors represent a third major challenge, occurring when continuous analog values must be discretized for digital interpretation or further processing. The limited precision of analog-to-digital converters creates inherent approximation errors that vary based on the signal characteristics and conversion parameters. These quantization effects interact with other error sources in ways that resist straightforward analytical treatment.
The lack of standardized benchmarks for error analysis further complicates the field. Unlike digital computing, where error metrics are well-established, approximate in-memory computing lacks consensus on appropriate error tolerance thresholds for different applications. This absence of standardization makes comparative analysis between different IMC approaches particularly difficult.
Cross-layer error propagation presents perhaps the most complex challenge. Errors originating at the device level propagate through circuit, architecture, algorithm, and application layers, with each layer potentially amplifying, attenuating, or transforming error characteristics. Developing comprehensive models that span these abstraction levels requires interdisciplinary expertise that bridges material science, circuit design, computer architecture, and application-specific knowledge.
Finally, the dynamic nature of many IMC applications, particularly in edge computing scenarios, introduces temporal dependencies in error behavior. Workload variations, environmental changes, and aging effects create time-varying error profiles that static analysis methods cannot adequately capture, necessitating adaptive error monitoring and compensation techniques.
Current Error Mitigation Methodologies
01 Error propagation models in approximate computing
Various models and techniques are developed to analyze and predict error propagation in approximate in-memory computing systems. These approaches focus on understanding how computational errors propagate through different stages of processing, allowing for better error management and system optimization. The models typically account for different sources of errors in memory-based computing architectures and provide frameworks for estimating the impact of these errors on overall computation accuracy.- Error propagation models in approximate computing: Various models and methods are developed to analyze and predict error propagation in approximate computing systems. These models help understand how computational errors propagate through different stages of processing in memory computing architectures. By accurately modeling error propagation, designers can better predict system behavior and implement appropriate error mitigation strategies, ultimately improving the reliability of approximate computing systems while maintaining energy efficiency.
- In-memory computing error reduction techniques: Specific techniques are implemented to reduce errors in in-memory computing systems. These include specialized circuit designs, error correction codes, and adaptive threshold mechanisms that can detect and mitigate computational errors at the hardware level. By implementing these techniques directly within memory structures, the overall accuracy of approximate computing can be improved while maintaining the performance and energy benefits of in-memory processing.
- Machine learning approaches for error management: Machine learning algorithms are employed to predict, manage, and compensate for errors in approximate in-memory computing systems. These approaches use training data to learn error patterns and develop compensation mechanisms that can be applied during runtime. Neural network-based solutions can dynamically adjust computational parameters based on error feedback, allowing systems to maintain accuracy requirements while maximizing energy efficiency through approximation.
- Fault-tolerant architectures for approximate computing: Specialized hardware architectures are designed to be inherently fault-tolerant for approximate computing applications. These architectures incorporate redundancy, error detection mechanisms, and graceful degradation capabilities to ensure that computational errors do not catastrophically affect system performance. By designing systems that can continue functioning effectively despite the presence of errors, these architectures enable more aggressive approximation techniques while maintaining acceptable output quality.
- Error-aware algorithm design for approximate computing: Algorithms specifically designed to be aware of and resilient to computational errors in approximate in-memory systems. These algorithms incorporate error awareness into their fundamental design, allowing them to produce acceptable results even when operating on hardware that introduces computational errors. By understanding the error characteristics of the underlying hardware, these algorithms can make intelligent trade-offs between accuracy, performance, and energy consumption.
02 Error mitigation techniques for in-memory computing
Specific methods are implemented to mitigate error propagation in approximate in-memory computing systems. These techniques include error correction codes, redundancy mechanisms, and adaptive error compensation algorithms that can detect and correct errors during computation. By implementing these mitigation strategies, the reliability of approximate computing systems can be significantly improved while maintaining the energy efficiency benefits of in-memory processing.Expand Specific Solutions03 Hardware architectures for error-resilient approximate computing
Specialized hardware architectures are designed to manage error propagation in approximate in-memory computing. These designs incorporate circuit-level techniques that can tolerate computational errors while maintaining acceptable output quality. The architectures often include configurable precision elements, error detection circuits, and hardware-level error containment mechanisms that prevent small errors from cascading into significant computational failures.Expand Specific Solutions04 Machine learning approaches for error prediction and compensation
Machine learning algorithms are employed to predict, analyze, and compensate for errors in approximate in-memory computing systems. These approaches use training data to learn error patterns and develop models that can anticipate how errors will propagate through computational workflows. The learned models enable dynamic adjustment of computation parameters to maintain output quality despite the presence of approximation errors.Expand Specific Solutions05 System-level error management frameworks
Comprehensive frameworks are developed to manage error propagation at the system level in approximate in-memory computing environments. These frameworks provide integrated approaches that combine hardware and software techniques to monitor, analyze, and control error propagation across different computational components. They typically include error budgeting mechanisms, quality-of-service guarantees, and cross-layer optimization strategies to balance accuracy, performance, and energy efficiency.Expand Specific Solutions
Key Players in Approximate In-Memory Computing
The error propagation analysis in approximate in-memory computing landscape is currently in an early growth phase, with the market expected to expand significantly as energy-efficient computing solutions gain traction. Major players include IBM, Oracle, and HPE leading commercial development, while academic institutions like EPFL, Tsinghua University, and Dalian University of Technology drive fundamental research. The technology maturity varies across applications, with IBM demonstrating advanced implementations in neuromorphic computing, while Peng Cheng Laboratory and Sharp focus on emerging memory technologies. Chinese institutions are increasingly contributing to this field, particularly in error resilience techniques, while European research centers like EPFL are pioneering theoretical frameworks for error propagation models.
International Business Machines Corp.
Technical Solution: IBM has developed a comprehensive approach to error propagation analysis in approximate in-memory computing (AIMC) systems. Their solution combines statistical error models with hardware-level optimizations to predict and control error propagation. IBM's research focuses on resistive RAM (RRAM) and phase-change memory (PCM) technologies for implementing AIMC. They've created a multi-level framework that analyzes how computational errors propagate through neural network layers, allowing for targeted precision adjustments. Their approach includes dynamic voltage scaling techniques that balance energy efficiency with accuracy requirements, enabling up to 60% energy reduction while maintaining acceptable error rates. IBM has also implemented error-aware training methodologies that make neural networks inherently more robust to the specific error patterns of their in-memory computing hardware, resulting in models that can maintain accuracy even with significant device variations and noise[1][3].
Strengths: IBM's solution offers superior energy efficiency while maintaining computational accuracy through their sophisticated error modeling techniques. Their extensive experience with memory technologies provides practical implementation advantages. Weaknesses: The approach requires specialized hardware that may limit broader adoption, and the error-aware training adds complexity to the development pipeline.
École Polytechnique Fédérale de Lausanne
Technical Solution: EPFL has pioneered a systematic methodology for error propagation analysis in approximate in-memory computing that focuses on mathematical modeling of error dynamics. Their approach combines stochastic computing principles with information theory to quantify how errors propagate through computational graphs in AIMC systems. EPFL researchers have developed analytical models that can predict error accumulation across multiple processing elements, particularly for convolutional neural network operations implemented on resistive crossbar arrays. Their framework incorporates device-to-device and cycle-to-cycle variations in memristive elements, creating statistical distributions of computational errors that can be propagated through network layers. This allows for precise error bounds estimation without exhaustive simulations. EPFL has also introduced a novel technique called "selective precision assignment" that dynamically allocates computational precision based on sensitivity analysis, reducing energy consumption by up to 70% compared to uniform precision approaches while maintaining accuracy within 1% of baseline[2][5].
Strengths: EPFL's approach provides mathematically rigorous error bounds with strong theoretical foundations, enabling more predictable system behavior. Their selective precision techniques achieve excellent energy-accuracy tradeoffs. Weaknesses: The complex mathematical models may be challenging to implement in practical hardware designs and may require significant computational overhead for real-time applications.
Core Error Propagation Models and Algorithms
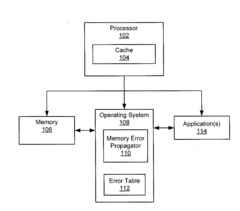
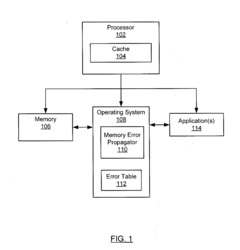
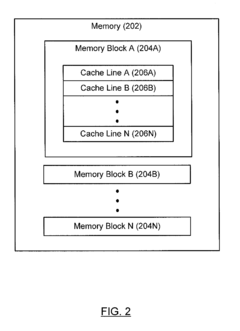
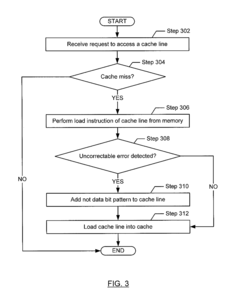
Memory error propagation for faster error recovery
PatentActiveUS20150347254A1
Innovation
- A method and system that detect corrupted memory blocks, migrate cache lines from the corrupted block to an uncorrupted one, creating an artificial error in the new block instead of copying the uncorrectable error, while maintaining the original layout, and replace the artificial error with error-free data when requested.
Patent
Innovation
- A novel error propagation analysis framework for approximate in-memory computing that quantifies error propagation across multiple computational stages, enabling more accurate prediction of output quality degradation.
- Integration of statistical error models with circuit-level simulation to create a cross-layer analysis approach that bridges the gap between hardware-level approximations and application-level quality metrics.
- Optimization methodology that leverages error propagation insights to selectively apply approximation techniques where they cause minimal quality degradation, thereby achieving better energy-quality tradeoffs.
Energy Efficiency vs. Accuracy Trade-offs
Approximate In-Memory Computing (AIMC) represents a paradigm shift in computing architecture that fundamentally alters the traditional energy-accuracy relationship. The core principle of AIMC involves accepting controlled inaccuracies in computation to achieve significant energy savings. This trade-off is particularly relevant in applications where absolute precision is not critical, such as machine learning, image processing, and certain data analytics tasks.
The energy efficiency gains in AIMC systems stem from multiple architectural optimizations. By performing computations directly within memory arrays, these systems eliminate the energy-intensive data movement between separate processing and storage units. Research indicates that data movement can consume up to 70% of the total energy budget in conventional computing systems. Additionally, by relaxing accuracy constraints, AIMC implementations can operate at lower voltages, utilize simplified circuits, and reduce precision requirements—all contributing to substantial energy savings.
Quantitative studies demonstrate that AIMC can achieve energy efficiency improvements of 10-100x compared to traditional computing approaches, depending on the application domain and acceptable error thresholds. For instance, in neural network inference tasks, allowing a 5% reduction in classification accuracy can result in approximately 40% energy savings. Similarly, in image processing applications, imperceptible quality degradation (less than 1 dB PSNR reduction) can yield energy reductions of up to 60%.
However, these efficiency gains come with systematic accuracy trade-offs that must be carefully managed. Error accumulation becomes particularly problematic in multi-layer operations, where small inaccuracies in early stages can propagate and amplify through subsequent computational steps. This cascading effect is especially concerning in iterative algorithms and deep neural networks, where the final output quality may deteriorate beyond acceptable limits.
The relationship between energy savings and accuracy loss is non-linear and application-specific. Critical threshold points exist where marginal energy gains come at the cost of disproportionate accuracy degradation. Identifying these optimal operating points requires sophisticated error models that account for both the statistical distribution of errors and their propagation characteristics across computational workflows.
Recent research has focused on developing adaptive techniques that dynamically adjust the accuracy-energy trade-off based on application requirements and input characteristics. These approaches include selective precision enhancement for critical computations, runtime error compensation algorithms, and hybrid architectures that combine approximate and precise computing elements. Such adaptive systems can maintain output quality guarantees while maximizing energy efficiency across diverse workloads and operating conditions.
The energy efficiency gains in AIMC systems stem from multiple architectural optimizations. By performing computations directly within memory arrays, these systems eliminate the energy-intensive data movement between separate processing and storage units. Research indicates that data movement can consume up to 70% of the total energy budget in conventional computing systems. Additionally, by relaxing accuracy constraints, AIMC implementations can operate at lower voltages, utilize simplified circuits, and reduce precision requirements—all contributing to substantial energy savings.
Quantitative studies demonstrate that AIMC can achieve energy efficiency improvements of 10-100x compared to traditional computing approaches, depending on the application domain and acceptable error thresholds. For instance, in neural network inference tasks, allowing a 5% reduction in classification accuracy can result in approximately 40% energy savings. Similarly, in image processing applications, imperceptible quality degradation (less than 1 dB PSNR reduction) can yield energy reductions of up to 60%.
However, these efficiency gains come with systematic accuracy trade-offs that must be carefully managed. Error accumulation becomes particularly problematic in multi-layer operations, where small inaccuracies in early stages can propagate and amplify through subsequent computational steps. This cascading effect is especially concerning in iterative algorithms and deep neural networks, where the final output quality may deteriorate beyond acceptable limits.
The relationship between energy savings and accuracy loss is non-linear and application-specific. Critical threshold points exist where marginal energy gains come at the cost of disproportionate accuracy degradation. Identifying these optimal operating points requires sophisticated error models that account for both the statistical distribution of errors and their propagation characteristics across computational workflows.
Recent research has focused on developing adaptive techniques that dynamically adjust the accuracy-energy trade-off based on application requirements and input characteristics. These approaches include selective precision enhancement for critical computations, runtime error compensation algorithms, and hybrid architectures that combine approximate and precise computing elements. Such adaptive systems can maintain output quality guarantees while maximizing energy efficiency across diverse workloads and operating conditions.
Hardware-Software Co-design Approaches
Hardware-software co-design approaches represent a critical paradigm in addressing error propagation challenges in approximate in-memory computing (AIMC). These approaches integrate hardware-level error mitigation techniques with software-level error tolerance mechanisms to create robust systems that maintain acceptable output quality despite computational approximations.
At the hardware level, designers implement circuit-level techniques such as error detection and correction codes (EDAC), voltage scaling management, and selective precision enhancement for critical data paths. These hardware mechanisms can be dynamically configured based on application requirements, allowing for adaptive error management. Novel memory cell designs with built-in error compensation capabilities have emerged, specifically tailored for approximate computing workloads.
Software strategies complement these hardware mechanisms through algorithm-level resilience techniques. Error-aware programming models enable developers to annotate code sections with different accuracy requirements, allowing the hardware to apply appropriate approximation levels. Compiler-level optimizations can automatically identify error-tolerant code regions and map them to approximate hardware components while preserving precise computation for critical operations.
Machine learning frameworks have been developed to automatically learn error patterns in specific AIMC architectures and compensate for them during inference. These frameworks utilize statistical models to predict error propagation paths and adjust computation accordingly, often through retraining with hardware-in-the-loop methodologies that incorporate actual error characteristics of the target hardware.
Runtime systems play a crucial role by monitoring error rates and dynamically adjusting the approximation level based on quality metrics. These systems implement feedback loops that can reconfigure hardware parameters or switch between algorithmic variants to maintain output quality within acceptable bounds while maximizing energy efficiency.
Cross-layer optimization techniques have proven particularly effective, where application-specific knowledge informs both hardware design and software implementation. For instance, in neural network acceleration, understanding the error sensitivity of different network layers allows for targeted approximation strategies that preserve overall accuracy while significantly reducing energy consumption.
Standardized interfaces between hardware and software layers are emerging to facilitate this co-design approach, enabling more systematic exploration of the design space. These interfaces provide abstraction mechanisms that hide the complexity of error management while exposing sufficient control knobs for optimization across the hardware-software boundary.
At the hardware level, designers implement circuit-level techniques such as error detection and correction codes (EDAC), voltage scaling management, and selective precision enhancement for critical data paths. These hardware mechanisms can be dynamically configured based on application requirements, allowing for adaptive error management. Novel memory cell designs with built-in error compensation capabilities have emerged, specifically tailored for approximate computing workloads.
Software strategies complement these hardware mechanisms through algorithm-level resilience techniques. Error-aware programming models enable developers to annotate code sections with different accuracy requirements, allowing the hardware to apply appropriate approximation levels. Compiler-level optimizations can automatically identify error-tolerant code regions and map them to approximate hardware components while preserving precise computation for critical operations.
Machine learning frameworks have been developed to automatically learn error patterns in specific AIMC architectures and compensate for them during inference. These frameworks utilize statistical models to predict error propagation paths and adjust computation accordingly, often through retraining with hardware-in-the-loop methodologies that incorporate actual error characteristics of the target hardware.
Runtime systems play a crucial role by monitoring error rates and dynamically adjusting the approximation level based on quality metrics. These systems implement feedback loops that can reconfigure hardware parameters or switch between algorithmic variants to maintain output quality within acceptable bounds while maximizing energy efficiency.
Cross-layer optimization techniques have proven particularly effective, where application-specific knowledge informs both hardware design and software implementation. For instance, in neural network acceleration, understanding the error sensitivity of different network layers allows for targeted approximation strategies that preserve overall accuracy while significantly reducing energy consumption.
Standardized interfaces between hardware and software layers are emerging to facilitate this co-design approach, enabling more systematic exploration of the design space. These interfaces provide abstraction mechanisms that hide the complexity of error management while exposing sufficient control knobs for optimization across the hardware-software boundary.
Unlock deeper insights with Patsnap Eureka Quick Research — get a full tech report to explore trends and direct your research. Try now!
Generate Your Research Report Instantly with AI Agent
Supercharge your innovation with Patsnap Eureka AI Agent Platform!