Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for quadratic curve trend extrapolation accuracy intelligent extension

A quadratic curve and trend extrapolation technology, applied in the field of 3D modeling, can solve the problem that the curve cannot be extended to the specified target, and achieve the effect of high precision

Inactive Publication Date: 2013-03-13
ANHUI UNIVERSITY OF TECHNOLOGY AND SCIENCE
View PDF4 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The aforementioned two patents solve the seamless splicing between two curves, which has strong practicability in CAD; however, the original characteristics of the curve cannot be extended to the specified target, which is also a problem often encountered in CAD applications

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for quadratic curve trend extrapolation accuracy intelligent extension
  • Method for quadratic curve trend extrapolation accuracy intelligent extension
  • Method for quadratic curve trend extrapolation accuracy intelligent extension

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

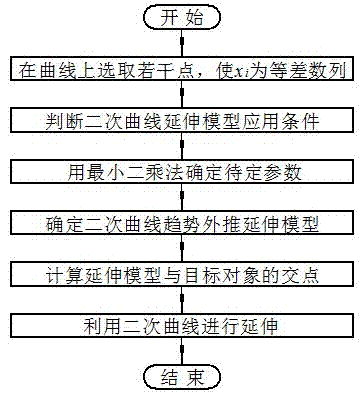
[0025] Referring to accompanying drawing 2, the expression of the quadratic curve 101 to be extended in this embodiment is , ; The target object 104 expression is ;Trend extrapolation and precise intelligent extension include the following steps:

[0026] (1) Select 9 points on the conic curve 101 to be extended: (-1.000, 0.500), (-0.884, 0.178), (-0.767, -0.090), (-0.651, -0.304), (-0.534, -0.464), (-0.418, -0.569), (-0.301, -0.620), (-0.185, -0.616), (-0.068, -0.559), the abscissa of the 9 points is an arithmetic sequence;

[0027] (2) Judging the application conditions of the quadratic curve extension model: the above-mentioned selection of 9 point sequences second difference of , ignoring the calculation error is a constant, and choose the intelligent extension of the quadratic curve;

[0028] (3) Use the least square method to determine the undetermined parameters: the extended model is , use the least squares method to determine the undetermined parameters as...

Embodiment 2

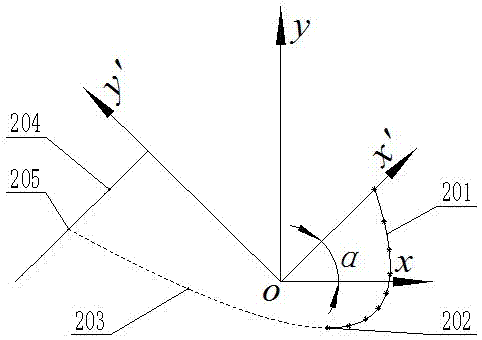
[0034] Referring to accompanying drawing 3, the expression of curve 201 to be extended in this embodiment is , ; The target object 204 expression is ;Trend extrapolation and precise intelligent extension include the following steps:

[0035] (1) Calculate the symmetry axis of the curve 201 and y Axis angle =45°, establish a Cartesian affine coordinate system with the coordinate origin , select 9 points on the curve 201: (1.000, 0.000), (0.875, -0.226), (0.750, -0.446), (0.625, -0.539), (0.500, -0.625), (0.375, - 0.664), (0.250, -0.656), (0.125, -0.602), (0.000, -0.500), the 9 points are in the coordinate system The middle abscissa is an arithmetic sequence;

[0036](2) Judging the application conditions of the quadratic curve extension model: the above-mentioned selection of 9 point sequences second difference of , ignoring the calculation error is a constant, and choose the intelligent extension of the quadratic curve;

[0037] (3) Use the least square method...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the field of three-dimensional (3D) modeling for computer graphics, in particular relates to polynomial surface graphics, and relates to a method for quadratic curve trend extrapolation accuracy intelligent extension. The conventional computer-aided design (CAD) software cannot extend a quadratic curve to be intersected with a designated object under the condition of maintaining the original characteristics. The method adopts a quadratic curve extension model to extend the quadratic curve, and comprises the following steps that: a plurality of points {,} are selected from the quadratic curve to be extended and form an arithmetic progression; the application conditions of the quadratic curve extension model are judged; undetermined parameters are determined through a least square method; the quadratic curve extension model is determined; the intersection points of the extension model and a target object are calculated; and the quadratic curve extension model is utilized to extend. The method can also be applied to the accuracy intelligent extension of arbitrary quadratic curve-shaped positions in a plane. The characteristics of the original curve are not changed after the curve is extended, long-distance accurate extension can be realized, the general key problem that the general CAD software cannot extend non-circular curves is solved, and the quadratic curve extension function of the conventional CAD software is added or completed.

Description

technical field [0001] The invention belongs to the field of 3D modeling for computer drawing, in particular to polynomial surface drawing, and relates to a method for extrapolating and intelligently extending quadratic curve trends. Background technique [0002] With the vigorous development of modern CAD software technology, many excellent two-dimensional and three-dimensional design software with friendly interface and powerful functions have emerged, such as AutoCAD, CAXA, Pro / E, UG, CATIA, etc. These softwares all have the basic function of extend, which can extend a straight line or arc to intersect a specified object, and keep the original characteristics (straight line or arc) unchanged. However, the extend function of these softwares is incapable of dealing with non-circular curves. If the extend command is used for a non-circular curve, some software (such as AutoCAD) will not perform any action; although some software (such as CAXA) performs the extension, it doe...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06T19/00
Inventor 刘有余张洁琼
Owner ANHUI UNIVERSITY OF TECHNOLOGY AND SCIENCE
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com