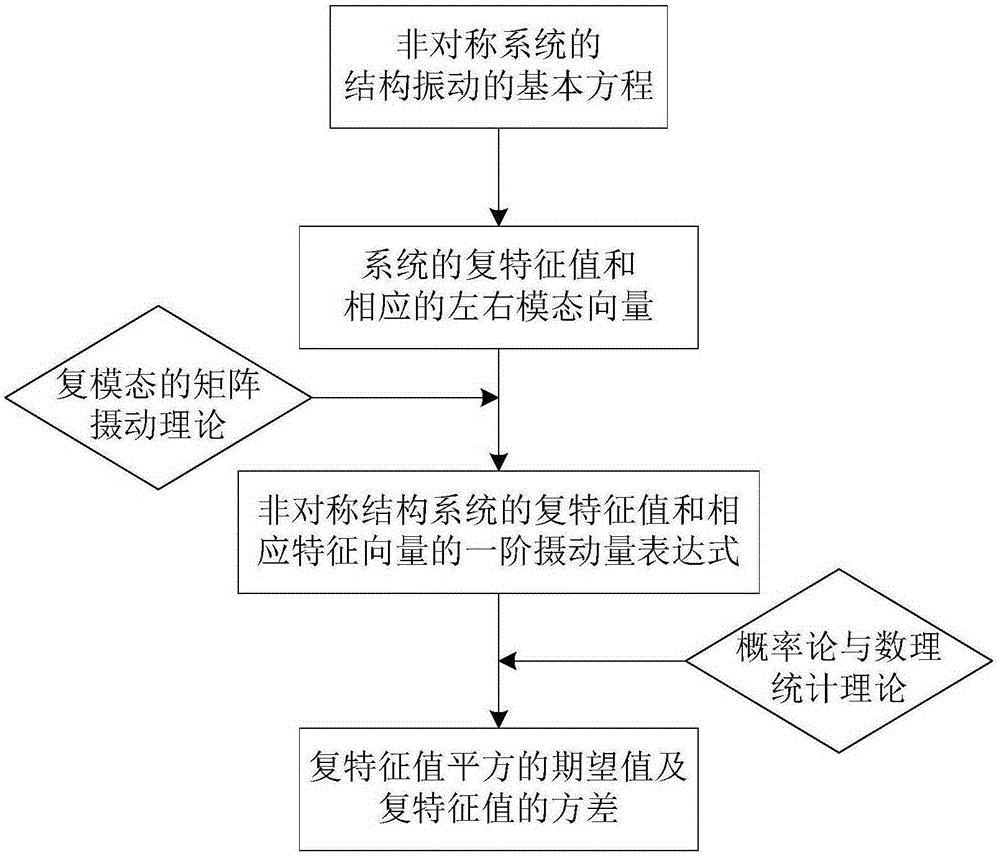
Complex mode random eigenvalue direct variance calculation method based on matrix perturbation theory

A technology of perturbation theory and random features, applied in complex mathematical operations and other directions, can solve the problems of perturbation methods, structural complex eigenvalues ​​and their statistical properties, etc.

Active Publication Date: 2015-12-23
BEIHANG UNIV +2
View PDF4 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] At present, the research and application of matrix perturbation theory by scholars at home and abroad mostly focus on the structural real mode matrix perturbation method when the structural parameters of the system are real symmetric matrices, and in the perturbation method of structural complex mode theory, structural complex eigenvalue There is still little research on its statistical properties

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Complex mode random eigenvalue direct variance calculation method based on matrix perturbation theory
  • Complex mode random eigenvalue direct variance calculation method based on matrix perturbation theory
  • Complex mode random eigenvalue direct variance calculation method based on matrix perturbation theory

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

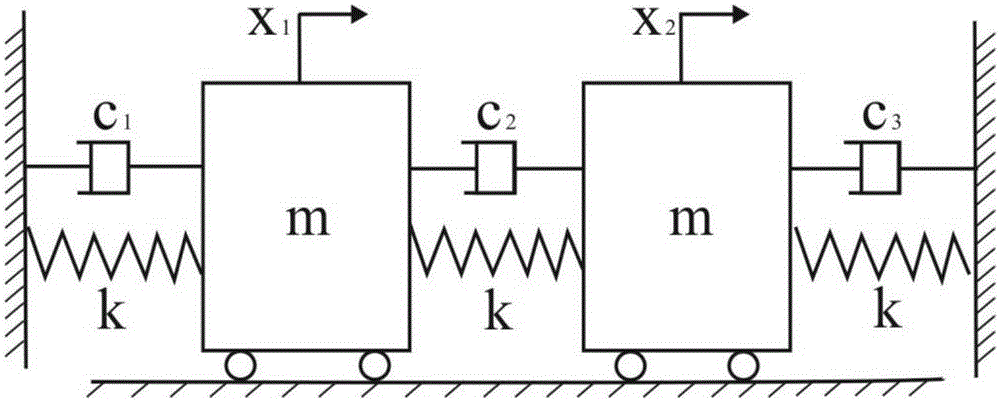
[0183] In order to understand more fully the characteristics of this invention and its applicability to engineering practice, the present invention uses figure 2 Taking the structural system as an example, the stochastic eigenvalue analysis of the complex mode is carried out. figure 2 middle c 1 ,c 2 ,c 3 Represent the damping coefficients of the three dampers in the system, k represents the stiffness coefficient of the spring in the system, m represents the mass of the slider, x 1 ,x 2 Respectively represent the position coordinates of the two sliders in the system.

[0184] Consider a two-degree-of-freedom vibration system that satisfies c=1, k=9, m=1, where the damping coefficient c 1 = c 2 = c 3 = c; use D'Alembert's principle to easily establish the differential equation of motion of the system:

[0185] m 0 0 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a complex mode random eigenvalue direct variance calculation method based on the matrix perturbation theory. According to the method, first, the complex mode eigenvalue of structure vibration and the first-order perturbation quantity of corresponding eigenvectors generated when the rigidity, the damping, the mass and other parameters of a structure are changed are derived according to the matrix perturbation theory; then, a direct variance calculation algorithm for calculating the change range of the structure complex mode eigenvalue is established based on the eigenvalue of the complex mode structure and the first-order perturbation quantity of the eigenvectors according to the probability theory. When complex eigenvalue analysis of an asymmetric structure system is performed, the change range of the complex mode eigenvalue of the structure system can be rapidly and accurately acquired without knowing or supposing correlation coefficient matrixes of structure parameters, and therefore engineering application of the method to large structures is greatly facilitated.

Description

technical field [0001] The present invention is applicable to the analysis of eigenvalues ​​of complex modal structural systems, and is used to solve the statistical properties and variation range of complex modal eigenvalues ​​of the structural systems under the condition of various disturbances. Modal eigenvalue analysis techniques provide guidance. Background technique [0002] As a practical tool for fast sensitivity analysis and fast structural reanalysis, the matrix perturbation method has received extensive attention in basic theory and engineering applications and has achieved considerable development. X.W.YANG and S.H.CHEN applied Padeapproximation to matrix perturbation theory, and obtained the expressions of eigenvector and eigenvalue variation. KaminskiM and SoleckaM expanded the structural eigenvalues ​​and eigenvectors with the method of chaotic polynomials (PCE), and studied the forced vibration response analysis of linear stochastic systems. DebrajG applied...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06F17/16
Inventor 仇翯辰邱志平王晓军王喜鹤何巍
Owner BEIHANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap