Eureka AIR delivers breakthrough ideas for toughest innovation challenges, trusted by R&D personnel around the world.

Chaotic-hash structuring method based composite non-linear digital wave-filter

A digital filter and construction method technology, applied in the field of information security, can solve the problems of destroying the global uniform distribution characteristics of PWL, the hash results are not evenly distributed, and it is difficult to resist statistical attacks, etc. It is easy to expand, realize software and hardware, and realize simple Effects of fast, resistant linear analysis

Inactive Publication Date: 2010-04-28
SOUTHWEST JIAOTONG UNIV
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

In 2003, Wang pointed out in Document 2 "Construction of One-way Hash Function Based on Generalized Chaotic Map Switching" (Wang Xiaomin et al. Acta Physica 2003 (52) 2737) that the algorithm is based on a specific chaotic system, which is easily deciphered by chaos prediction technology. At the same time, the effective word length precision effect will lead to the short-period behavior of the chaotic sequence, which will degrade the performance of the algorithm and other problems, and propose a chaotic hash construction method based on generalized chaotic map switching
Although Document 5 uses a piecewise linear map (PWL) with uniform distribution characteristics, the structure of PWL is changed by using variable parameters in each iteration, which essentially destroys the global uniform distribution characteristics of PWL, making the hash result in The hash space is not uniformly distributed, but related to the statistical properties of plaintext, so it is difficult to resist statistical attacks

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Chaotic-hash structuring method based composite non-linear digital wave-filter
  • Chaotic-hash structuring method based composite non-linear digital wave-filter
  • Chaotic-hash structuring method based composite non-linear digital wave-filter

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

[0025] The general method of the chaotic hash construction method based on the composite nonlinear digital filter of the present invention is:

[0026] 1) Initialization:

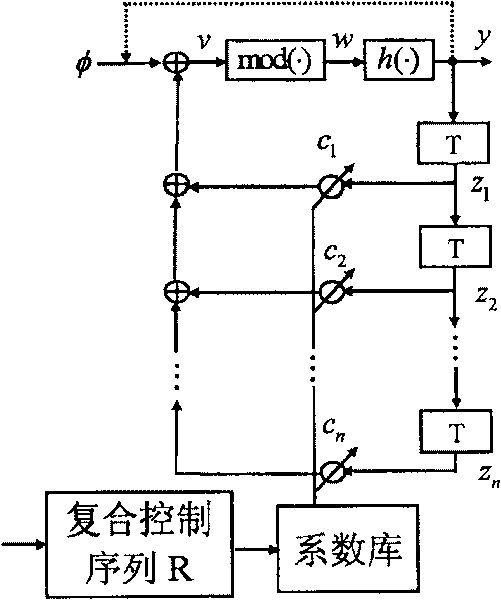
[0027] figure 1 Show: an n-dimensional nonlinear autoregressive digital filter can be expressed as Where φ∈(-1,1) is the initial input signal of the filter, {z 1 ,z 2 ,…z n }∈(-1, 1) is the initial state of the filter, {c 1 , C 2 ,...C n } Is the filter coefficient, T is the unit delay, h(·) is the nonlinear transfer function, mod(·) is the hardware overflow function, y is the output of the filter. When the filter satisfies the Kelber condition, that is, it satisfies the following three conditions: ①Coefficient |cn|>1, ②The absolute value of the characteristic root of the filter is not 1; ③The nonlinear transformation h(·) has uniform distribution characteristics; the output y of the filter is ergodic and maintains an n-dimensional uniform distribution, and the filter becomes a n Dimensional chaotic system....

Embodiment 1

[0035] n=2-dimensional nonlinear digital filter, k=2 sets of coefficients pre-stored in the coefficient library, and a chaotic hash construction method when the hash length L=128.

[0036] 1) Initialization:

[0037] n-dimensional autoregressive nonlinear digital filter, n=2, p=1, parameter library pre-stored k=2 p =2 sets of coefficients {c 0 =[3.57, 4], c 1 =[5.7,7]}, the hash length L=128 bits, the initial value of the filter is the key SK={φ 0 ,z 1 ,z 2 }={φ 0 = 0.5648, z 1 = -0.564, z 2 =0.679}, the initial hash value Nonlinear mapping Hardware overflow function Quantization function of filter output To simplify the length, take the plaintext M′ to be hashed = {0101110101}, and the length of the plaintext M filled with zeros is That is, s=2, and the filled content is Group M according to the length of 128 and mark it as M=(M 1 , M 2 ),

[0038] 2) Hash value generation:

[0039] ①The first paragraph of plaintext M 1 The hash value generation: will With M 1 XOR, get compou...

Embodiment 2

[0050] n=3-dimensional nonlinear digital filter, k=4 sets of coefficients pre-stored in the coefficient library, and a chaotic hash construction method under the condition that the hash length L=256.

[0051] 1) Initialization:

[0052] n-dimensional autoregressive nonlinear digital filter, n=3, p=2, parameter library pre-stored k=2 p =4 sets of coefficients {c 0 =[2.53, -0.63, 2], c 1 =[5.1, 1.2, 5], c 2 =[-3.64, 4.23, 3], c 3 =[0.75, 3.24, 4]}, the hash length L = 256 bits, the initial value of the filter is the key SK = {φ0, z 1 ,z 2 ,z 3 }={φ 0 = 0.5648, z 1 = -0.564, z 2 = 0.679, z 3 =0.132}, the initial hash value The nonlinear mapping h(w), the quantization function T(x) output by the filter, and the hardware overflow function mod(.) are all the same as in the first embodiment. To simplify the length, we also take the plaintext M'to be hashed = {0101110101}, and the length of the plaintext M filled with 0 is That is, s=2, and the filled content is Group M according to leng...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

Under control of composite sequence generated by plaintext, sub system of autoregressive non-linear digital filter modulates plaintext to chaos locus in high dimension in composite filter. Hashed value of plaintext is produced by quantizing chaos locus in coarse granulation. Iterative initial point of composite filter is as cipher key of algorithm, which satisfies requirement of security of Hash algorithm with cipher key. Sensitivity and traversing characteristic on initial value of chaos in high dimension makes hashed result sense to plaintext exceedingly. Moreover, hashed result is distributed in hashed space evenly. The composite sequence increases randomness selected by sub system of filter so as to guarantee complex sensitive nonlinear relation between iterative locus and initial condition. Thus, the invention possesses better scrambling, and stronger capability for anti deciphering. Features are: simple and fast algorithm, easy of modularized realization.

Description

Technical field [0001] The invention relates to a hash construction method for extracting message digests in the technical field of information security, and can be widely used in security applications such as digital certificates, electronic signatures, password protection, and integrity verification of digital information. Background technique [0002] With the rapid development of e-commerce and information digitization, hashing algorithms are widely used in network-based security applications such as digital certificates, digital signatures, identity authentication and information integrity protection. Classical hash algorithms such as MD5 (Message Digest 5, Message Digest Algorithm 5) and SHA (SecureHash Algorithm) have been widely used in e-commerce such as finance and securities and have become the two de facto standards. Since the 1990s, people have conducted security attacks on these two algorithms, and have successively proposed deciphering methods such as "birthday att...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/00H04L9/32
Inventor 张家树王小敏
Owner SOUTHWEST JIAOTONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com