Method for constructing multi-system LDPC code check matrix of orderly arranged non-zero elements
An LDPC code, non-zero element technology, applied in the field of communication, can solve the problems of complex coding, large coding delay, large storage unit and calculation unit, etc., to achieve the effect of shortening the decoding time
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
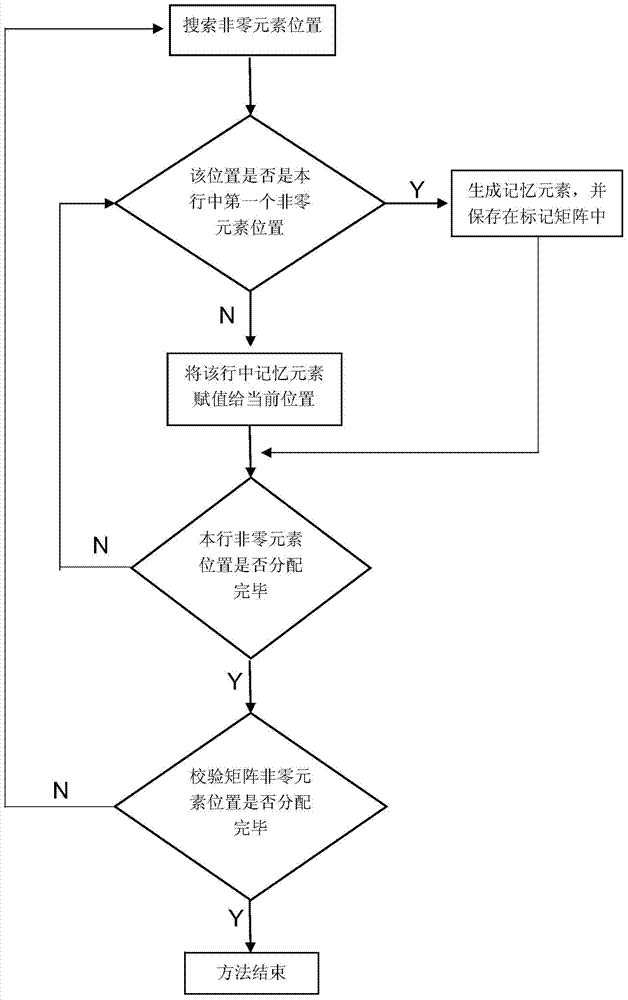
[0040] This example provides a brand-new element allocation idea for a construction check matrix algorithm of multi-ary LDPC codes - PEG algorithm. In it, the non-zero elements are assigned artificially or randomly at the relevant positions, so that each row has the same non-zero elements, and the basic operation steps are the assignment of non-zero position elements in each row, which runs through the entire check matrix construction process.
[0041] The present invention is based on the basic construction of the multi-ary LDPC code check matrix. The multi-ary LDPC code is mainly characterized by a sparse parity check matrix H. There are only a few non-zero elements in the parity check matrix, and most of the elements are zero.
[0042]
[0043] The check matrix H of the above multi-ary LDPC code has a dimension of m×n. Among them, the non-zero elements are represented by α, β, γ, ..., δ, ε, and {α, β, γ, ..., δ, ε}≤q-1, and α≠β≠γ≠...≠δ≠ε≠ 0. Each non-zero element can b...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com