Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Orthogonal basis training method based on Schmidt orthogonalization

A technology of Schmidt orthogonalization and training method, applied in the field of sparse representation, which can solve the problems of poor sparse effect

Inactive Publication Date: 2014-09-03
HARBIN INST OF TECH
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

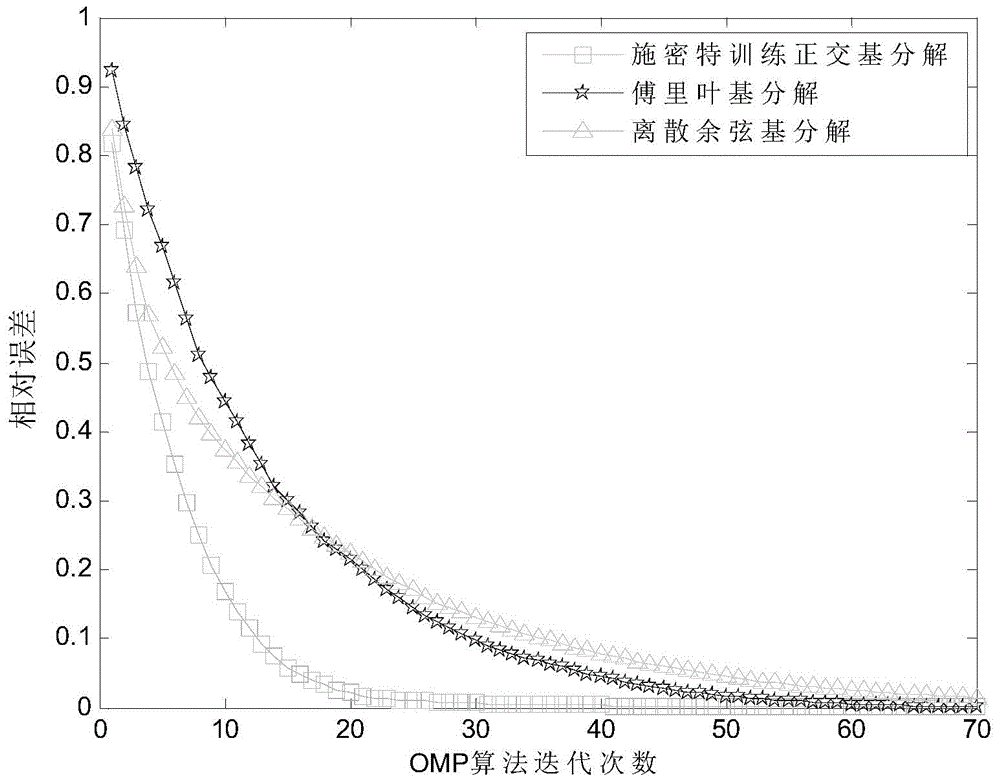
[0023] The present invention aims to solve the problem of poor sparsification effect in the prior art, and provides an orthogonal basis training method based on Schmidt orthogonalization

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Orthogonal basis training method based on Schmidt orthogonalization
  • Orthogonal basis training method based on Schmidt orthogonalization
  • Orthogonal basis training method based on Schmidt orthogonalization

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

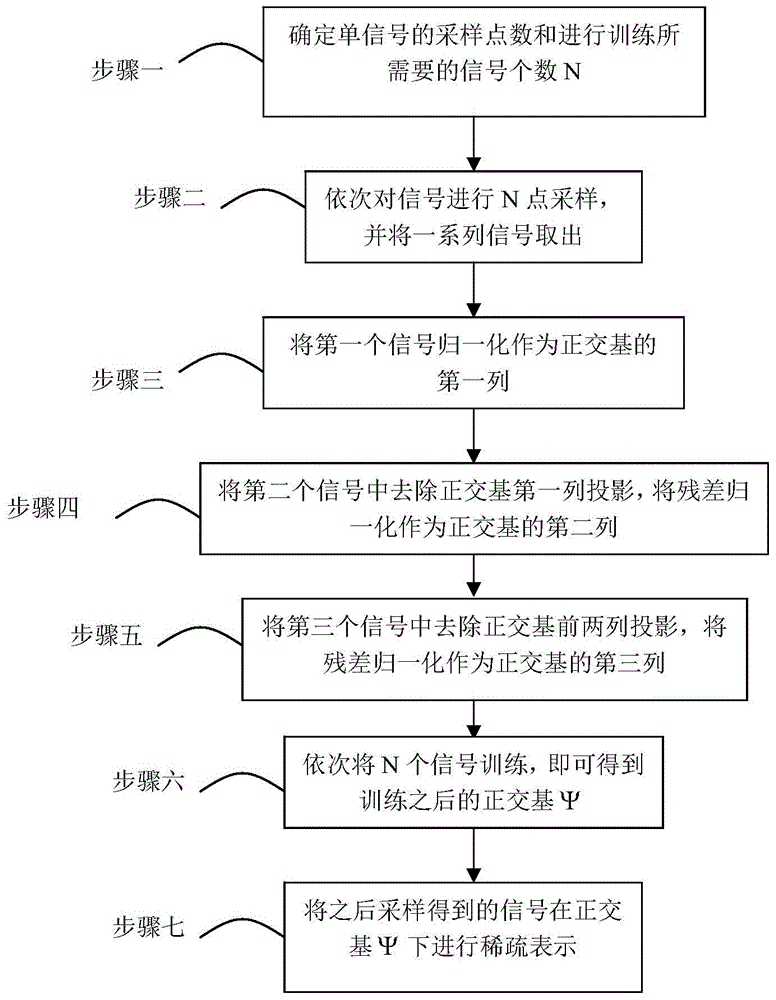
[0038] Specific implementation mode one: a kind of orthogonal basis training method based on Schmidt orthogonalization in this implementation mode is realized according to the following steps:

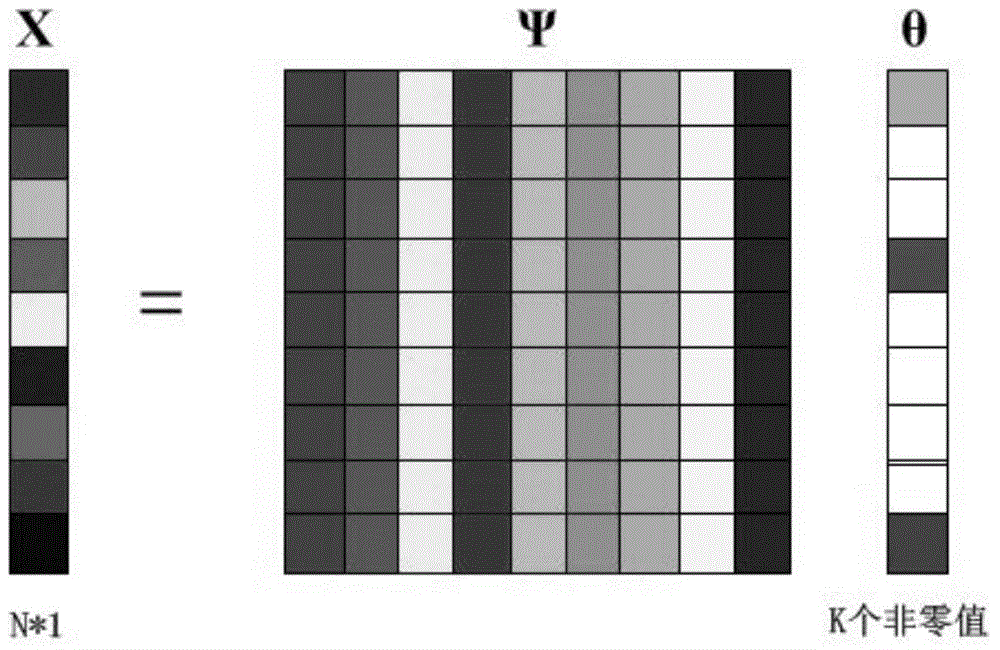
[0039] Step 1. Determine the number of sampling points of a single signal and the number N of signals required for training. The samples are arranged in columns to form a matrix X=[x 1 ,x 2 ,...x n ];

[0040] Step 2. Sampling the signal at N points in turn, and taking out a series of signals, where each signal x i (i=1,2,...N) is an N×1-dimensional vector;

[0041] Step 3, normalize the first signal as the first column of the orthogonal basis;

[0042] Step 4, remove the first column projection of the orthogonal basis from the second signal, and normalize the residual as the second column of the orthogonal basis;

[0043] Step 5, remove the first two columns of the orthogonal basis from the third signal, and normalize the residual as the third column of the orthogonal basis;

[...

specific Embodiment approach 2

[0046] Embodiment 2: This embodiment differs from Embodiment 1 in that: the N signals in step 1 are signals received by the receiving end at equal time intervals.

[0047] Other steps and parameters are the same as those in Embodiment 1.

specific Embodiment approach 3

[0048] Specific implementation mode three: the difference between this implementation mode and specific implementation mode one or two is: the specific process of step three is:

[0049] when the first signal x 1 Upon arrival, the signal is normalized as the first column of the orthogonal basis which is

[0050] Other steps and parameters are the same as those in Embodiment 1 or Embodiment 2.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the signal processing field, and relates to signal sparse representation methods, in particular to an orthogonal basis training method based on Schmidt orthogonalization to solve the problem that in the prior art, the sparse effect is poor. The method comprises the steps that firstly, the sampling number of a single signal and the number N of signals needed by training are determined, and samples are arranged in row to form a matrix meeting the formula: X=[x1, x2, ..., xn]; secondly, N point sampling is carried out on signals in sequence; thirdly, the first signal is normalized to serve as the first row of the orthogonal basis; fourthly, a first row projection of the orthogonal basis of the second signal is removed, and the residual is normalized to serve as a second row of the orthogonal basis; fifthly, first two rows of projections of the orthogonal basis of the third signal are removed, and residual is normalized to serve as a third row of the orthogonal basis; sixthly, the N signals are trained in sequence, and then the trained orthogonal basis psi can be obtained; the signals are decomposed in the trained orthogonal basis, and then a good sparse representation can be obtained.

Description

technical field [0001] The invention relates to a signal sparse representation method, in particular to the construction of a sparse representation orthogonal base and the sparse representation of a signal under the orthogonal base obtained through training. Background technique [0002] In signal analysis, the representation of signals often takes two basic forms: time domain form and frequency domain form. From the time-domain description of the signal, some characteristics of the signal can be distinguished, such as the speed of change, the range of values, continuous or discrete, etc. However, sometimes the frequency-domain description of the signal is more concerned by people. Some problems that cannot be seen clearly in the time domain are clear at a glance in the frequency domain. Compared with the time domain analysis method, the frequency domain analysis method has many outstanding advantages, especially the introduction of the fast Fourier transform makes the freq...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F19/00
Inventor 高玉龙朱尤祥陈艳平张蔚马永奎李然
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com