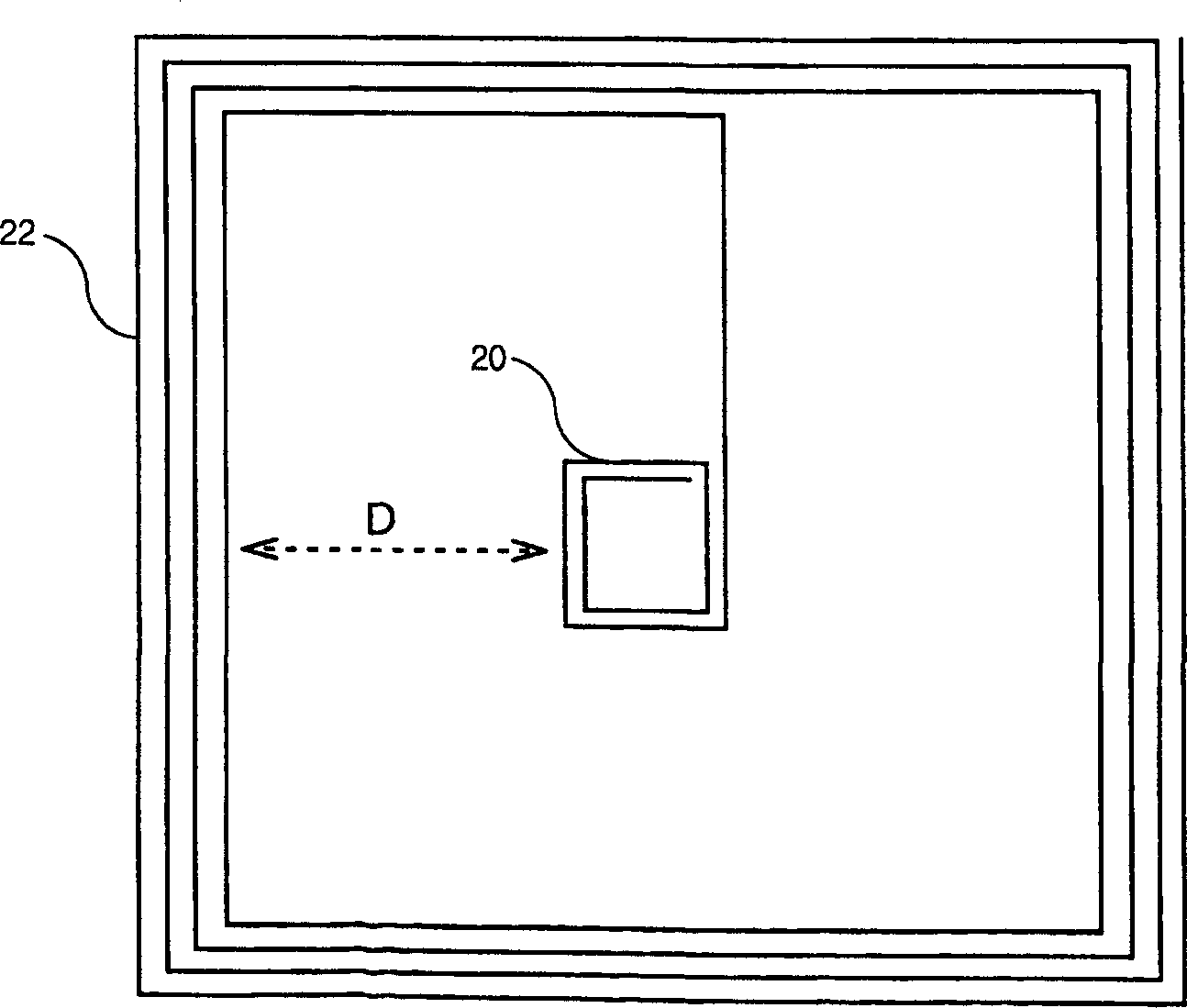
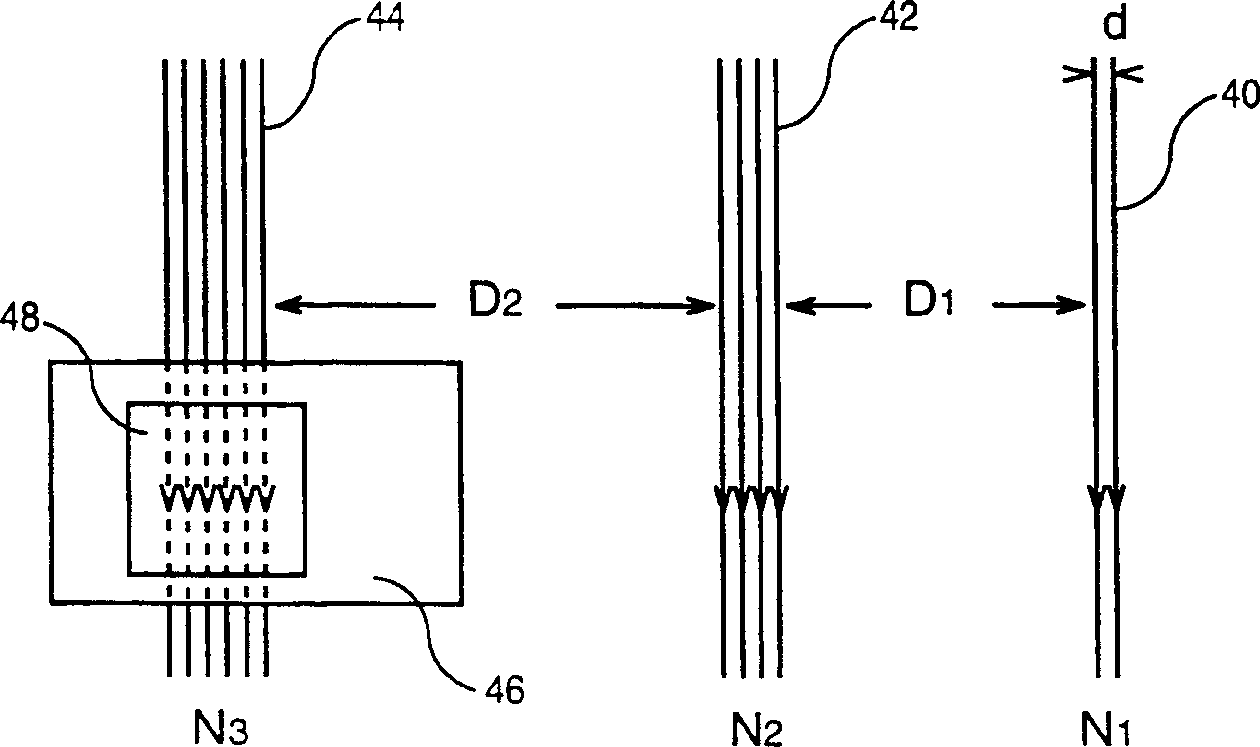
[0021] Such as figure 1 As shown in the conventional antenna 10 featuring multiple turns 12, 14, 16 generates a magnetic field that varies with where it is located. In this way, the value is positive in the section inside the turns, while the field outside the turns is negative. At the midpoint between the two turns and if the magnetic field caused by the turns of the other parts is negligible (because it decreases in the opposite direction with the distance, it is weak), because the positive magnetic field caused by the turns and the other turns The negative magnetic field with the same absolute value caused by the strands, the combined magnetic field is zero.
[0022] The indeterminate magnetic field is the main problem in generating the electromagnetic signal emitted by the antenna. The surface of the reader on which the carrier is shown on the front is generally square (or rectangular), and each side is 15 cm to 20 cm. If the antenna is too centered on the surface, there is a negative magnetic field outside the turns. However, if the turns of the antenna are located on the periphery of the surface of the reader, the magnetic field is positive on the entire surface of the reader (in the antenna), although the farther away from these turns, the greater the decrease in inverse proportion to the distance Magnetic field, there is a blind zone in the center of the surface. If the carrier is displayed in front of the blind zone, the carrier cannot receive enough energy. In addition, the solution consisting of significantly increasing the number of turns in order to strengthen the magnetic field is not applicable. Because increasing the surface area occupied by these turns also increases the number of sections where the magnetic field is zero.
[0023] Therefore, the solution proposed by the present invention consists of using an antenna consisting of n series of turn groups, and each turn group k (where k varies from 1 to n-1) is included in the group k+1, and The ends of the outer turns in group k are connected to the ends of the inner turns in group k+1. The number of turns in group k is less than the number of turns in group k+1. Finally, in the same direction, for example, from group 1 to group n counterclockwise, wind each turn in all turn groups.
[0024] figure 2 An example of an embodiment in the form of two groups is shown in, where the first group of turns 20 includes two rectangular turns and the second group 22 includes four rectangular turns with a distance D from the first group.
[0025] If we study the left vertical strands of three successive turn groups 40, 42, 44 image 3 , The magnetic field generated by the turn group 40 is outside, that is, on the left side of the group 40, which is negative. However, the presence of the turn set 42 surrounding the turn set 40 can generate a positive magnetic field within these turns and especially in the gap between the set 40 and the set 42.
[0026] Generally speaking, the magnetic field induced by the lm-wide metal wire in which the current I circulates has a value represented by the curve shown in FIG. 4. The magnetic field is zero at the center of the wire. If the origin of the abscissa is in the middle of the line, the magnetic field then increases rapidly and reaches a relatively constant value as follows: H 1 = K 1 . I 2 πl m For 0 m
[0027] Then, the value of H decreases as the inverse function of the abscissa as follows: H 2 = K 2 . I 2 πx For x>l m
[0028] Thus the value of the magnetic field generated by the group of N turns is:
[0029] H=0 for x=0
[0030] H = K 1 . NI 2 πl m For 0 m
[0031] H = K 2 NI 2 πx For x>l m
[0032] Back to image 3 , The value of the magnetic field generated by each turn group 40 or 42 in the space separated by this group can use the curves shown in FIGS. 5A and 5B respectively, where the origin of the abscissa is taken as the midpoint of the turn group 42. Note the field (H 1 ) Is positive, and the field (-H 2 ) Is negative.
[0033] The value of the composite field in the space between groups 40 and 42 (H R ) Is the algebraic sum of the fields shown in Figures 5A and 5B. The value of this field shown in Figure 5C is:
[0034] H R =H 1 -H 2
[0035] It can be seen that the value of the composite field is first positive, and then from the distance D’ from the turn group 42 1 It is negative at first. If D1 and D’ 1 (From D’ 1 The difference between the initial composite field is negative) is not very obvious and is much smaller than the minimum size of the antenna on the one-time ticket, it does not matter, because the average value of the field received by the ticket remains positive and must be greater than the guaranteed ticket The minimum required value. However, it is possible to divide the distance D 1 Choose to be equal to D’ 1So that the section is reduced to zero, thereby providing a field that is all positive in the space between the two turn groups. To achieve this, the negative field -H 2 The maximum absolute value of must be less than or equal to the positive field + H 1 The smallest absolute value of; this is approximately K 1 . = N 1 I 2 πl m 1 ≤ K 2 N 2 I 2 π D 1
[0036] or
[0037] K 1. N 1. D 1. ≤K 2. N 2. l m1
[0038] As an initial approximation, if two coefficients K are allowed 1 And K 2 Equal, we can get:
[0039] N 1. D 1 ≤N 2. l m1 lm 1 Must be less than D 1 , It can be seen that through the N 1 And N 2 Choose appropriate values to make: N 2 N 1 ≥ D 1 l m 1 Or, more generally, between two successive turn sets k and k-1 (where k changes from 2 to n), let: Nk Nk - 1 ≥ Dk - 1 l m ( k - 1 ) The inequality can be made true.
[0040] It should be noted that the positive field generated by the turn group 42 within these turns is added to the positive field generated by the turn group 40, although the value of the increase becomes smaller due to the weakening of the field as the distance from the turn group 42 becomes smaller. Similarly, the turn group 44 surrounds the turn group 42. In the section between the two turn sets, the positive magnetic field generated by the turn set 44 within these turns compensates for the negative magnetic field generated by the turn set 42 (and the negative magnetic field generated by the turn set 40). This can be done if there are enough turns. It is allowed to establish a positive magnetic field or at least a positive average field in this section. Please note that the positive magnetic field generated by the inner turn group 44 within the turn group 42 is added to the positive field generated by the turn group 42 and is also added to the positive field generated by the turn group 40 within the turn group 40, but gradually increases with distance The field gradually weakened.
[0041] It is possible to recursively set n turn groups with increasing turns on the antenna support so as to cover the entire antenna surface of the reader. However, there is a parameter that defines the number n of turn groups in the antenna: it is the distance between the turn groups, that is, D between the first group and the second group 1 , D between the second and third groups 2 , And so on, and finally D between groups n-1 and n n-1. Distance D 1 (Between groups 40 and 42) or D 2 (Between groups 42 and 44) must be optimal. To avoid the previous reference figure 1 The magnetic field around the midpoint mentioned is accumulated, it must not be too small. However, the distance must not be too large so that the positive magnetic field is high enough to compensate for the negative magnetic field established by the previous turn group outside its turns.
[0042] There is a decision parameter that also determines the structure of the antenna according to the present invention. In fact, the one-time ticket must receive a positive average field at all points of the reader and especially when it is on a certain set of turns of the field generated as zero. The smallest side of the ticket antenna must therefore be greater than image 3 The width of each turn group shown in, and the width of the antenna 48 on the ticket 46 must be greater than the total width of the widest turn group 44. Since the closer to the periphery of the antenna each turn group increases its number of turns, it is mandatory to reduce the metal width of the turn when going from one turn group to another larger turn group so that the width of the turn group is always smaller than that on the ticket The minimum size of the antenna. Thus, in addition to being applied to figure 2 In addition to the following inequalities of the example shown in: N 2 N 1 ≥ D 1 l m 1 N 3 N 2 ≥ D 2 l m 2 The following inequality must also be true:
[0043] l m1l m2l m3
[0044] While always observing the inequalities mentioned above, it is clear that the more the number of turns of an outer turn group, such as N 3 , You can also increase the distance between the turn group and the nearest inner turn group, such as D 2.
[0045] It should be noted that the distance d separating two turns in each turn group should be as small as possible, that is, the minimum distance allowed in turn processing. More generally, the distance d is smaller than the distance D in magnitude. In other words, the ratio between the distance D and the distance d must be greater than a predetermined preferred value. As a result, if the width between turns has a given value d, it means that the distance D must be greater than a certain predetermined value.
[0046] Thanks to the successive turn sets described above, it is possible to obtain a sufficiently high field for the reader for the card and for the one-time ticket. In addition, this structure also allows a relatively uniform field to be obtained over the entire surface of the reader, which does not exceed the standard predetermined field value that can be applied to a non-contacting body. This is demonstrated through the following three examples shown in Figures 5, 6 and 7, where the origin of the abscissa is at the center of the reader, and the following assumptions are made:
[0047] -One-time ticket features a square antenna with a size of 2cm×2cm,
[0048] -The size of the reader is 20cm×20cm,
[0049] -The minimum field generated for the card is 0.8A/m,
[0050] -The minimum field for a one-time ticket is 2A/m,
[0051] -The field value that does not have to be exceeded is 7.5A/m,
[0052] -The current in each turn is 50 mA.
[0053] 1. in Figure 6 In the first case shown in, the feature of the reader is a simple antenna consisting of 4 concentric turns on the periphery of the reader, the metal width of the turns is 1mm and the distance between turns is 1mm. Note that the maximum field is 15A/m at the periphery, so it is greater than the allowable threshold. However, the field near the center of the reader is only 0.8 A/m, so it is high enough for a card reader but not high enough for a one-time ticket reader.
[0054] 2. In the second case shown in Fig. 7, the antenna of the reader according to the invention consists of three turn groups:
[0055] -The first group of 2 turns with a size of 6cm×6cm, the metal width is 0.3cm and the width between turns is 0.1mm,
[0056] --The second group of 4 turns with a size of 17cm×17cm, where the metal width is 0.3cm and the width between turns is 0.1mm,
[0057] -The third group of 6 turns with a size of 20cm×20cm, in which the metal width is 1mm and the width between turns is 0.1mm,
[0058] It can be noted that the minimum field is 2A/m, which is high enough for reading a one-time ticket or card, and the maximum field is 7.5A/m, which is equal to the limit threshold.
[0059] 3. In Figure 8 In the third case shown in, the antenna of the reader is similar to the antenna in the second case, except for the third turn group, which has a metal width equal to 0.3 cm instead of 1 mm.
[0060] It can be noticed that the field becomes negative in the space between the second turn group and the third turn group; this is because the metal width is not reduced in the third turn group which has more turns than the second turn group. Cause.
