A state update method for fractional linear discrete-time systems dealing with non-Gaussian lévy noise
A discrete system and state update technology, applied in the direction of complex mathematical operations, can solve problems that are difficult to be satisfied, and achieve the effect of solving limited problems
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0032] Below in conjunction with specific embodiment, further illustrate the present invention, should be understood that these embodiments are only used to illustrate the present invention and are not intended to limit the scope of the present invention, after having read the present invention, those skilled in the art will understand various equivalent forms of the present invention All modifications fall within the scope defined by the appended claims of the present application.
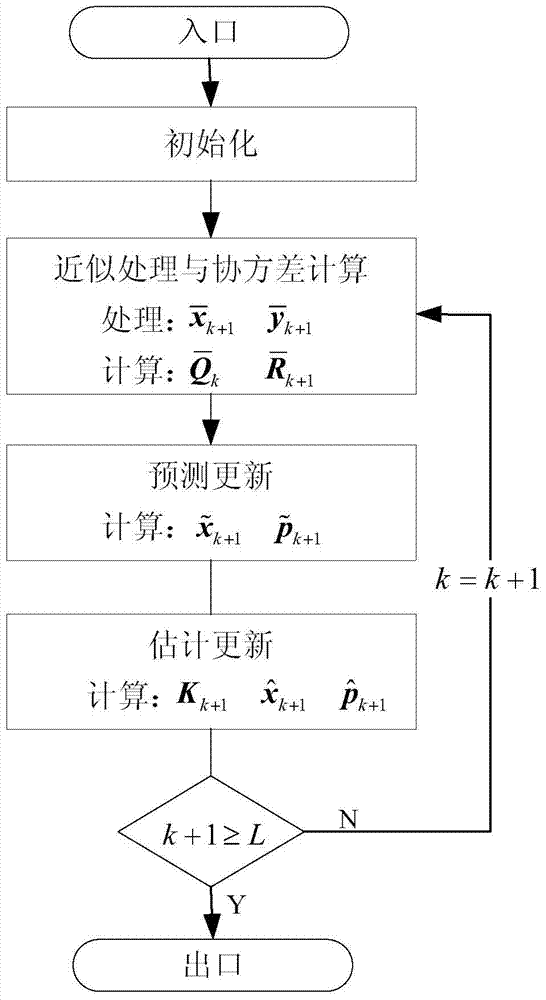
[0033] Such as figure 1 As shown, the fractional-order linear discrete system state update method for dealing with non-Gaussian Lévy noise includes the following steps:
[0034] (1), initialization. Including: setting the initial value of the state prediction quantity and the initial value of the prediction error covariance.
[0035] (2) Approximating the non-Gaussian Lévy noise, deriving the approximate value of the state and the approximate value of the measurement output.
[0036] (3) Calcul...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com