Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Lagrange function based least-squares multi-objective optimization method

A multi-objective optimization and least squares technology, applied in complex mathematical operations, biological neural network models, etc.

Inactive Publication Date: 2012-09-12
高俊文 +1
View PDF0 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] However, due to the large number of inversion operations in the above method, and practical problems often do not allow negative weight problems

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Lagrange function based least-squares multi-objective optimization method
  • Lagrange function based least-squares multi-objective optimization method
  • Lagrange function based least-squares multi-objective optimization method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

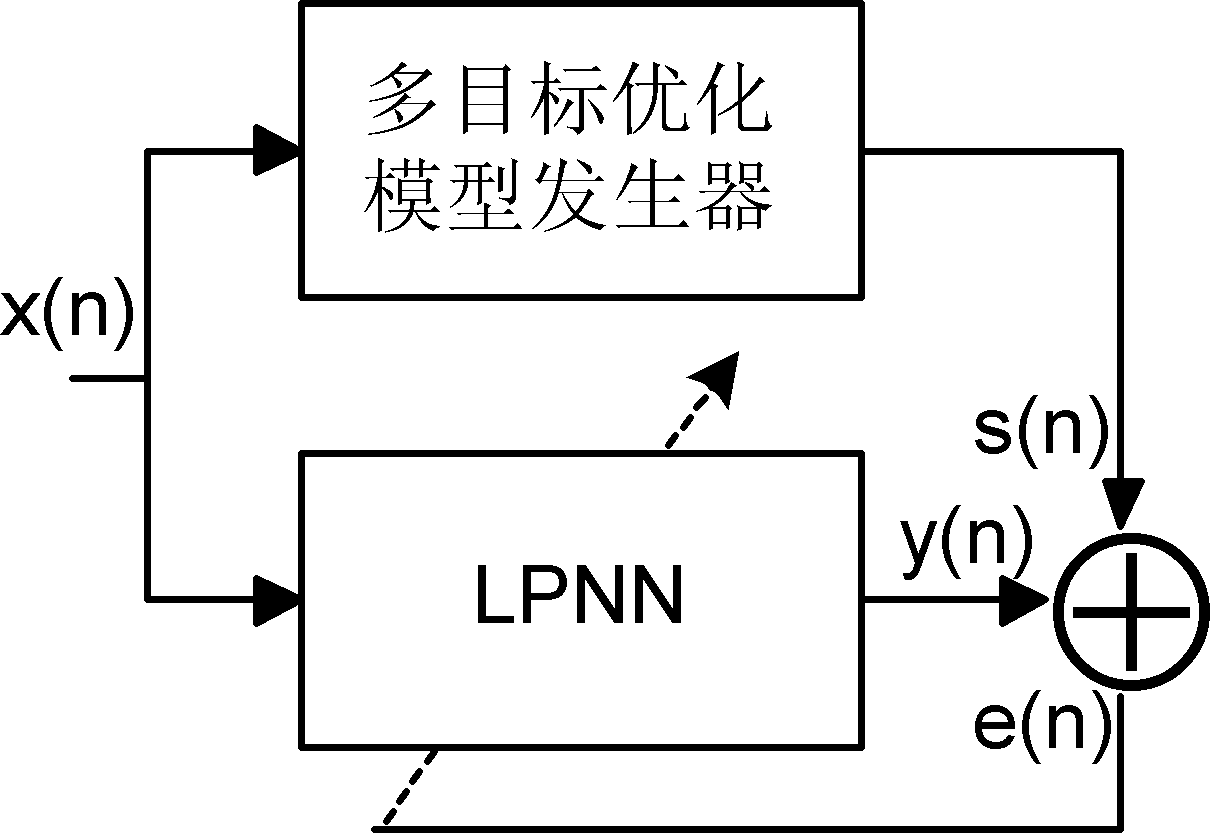
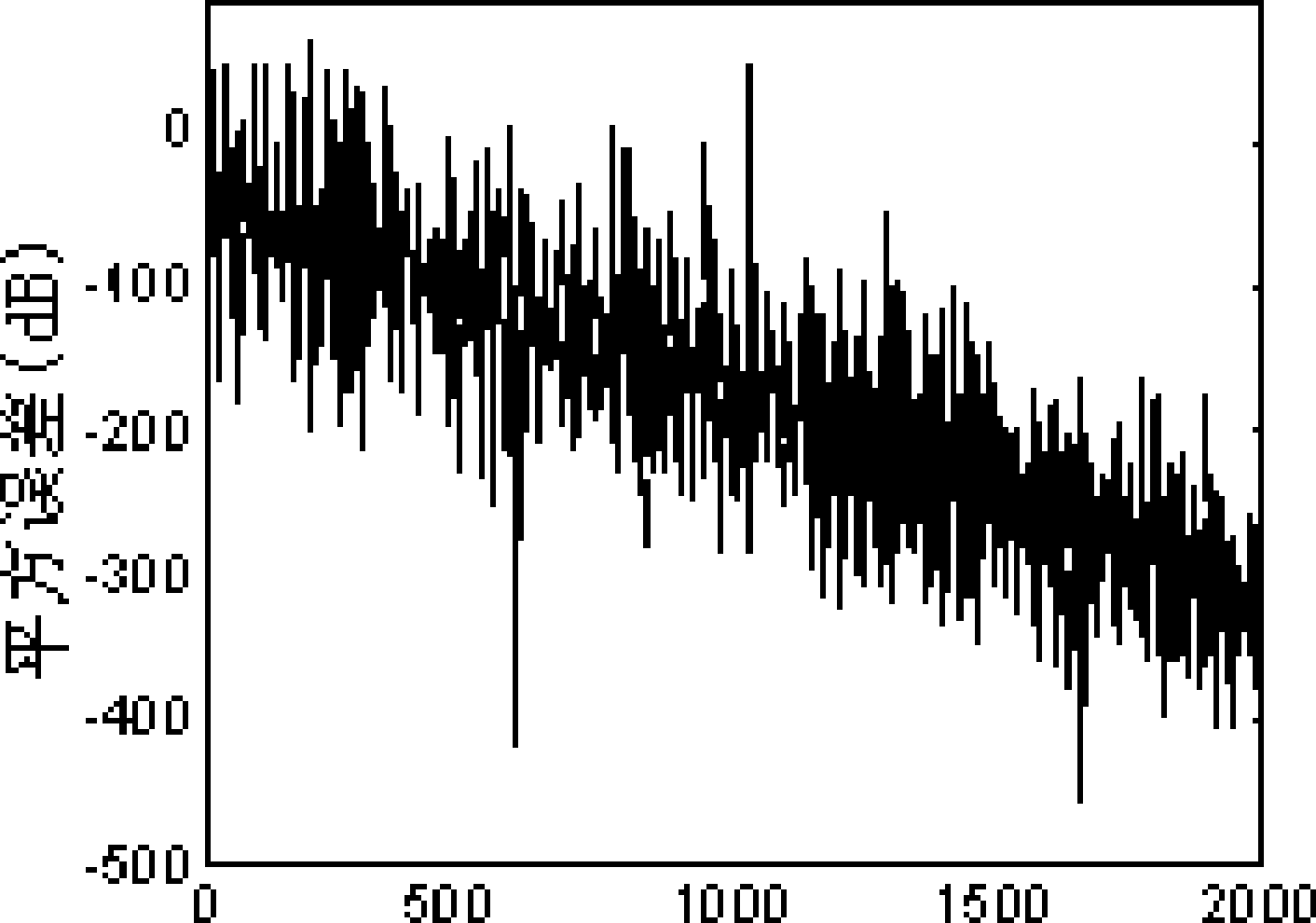
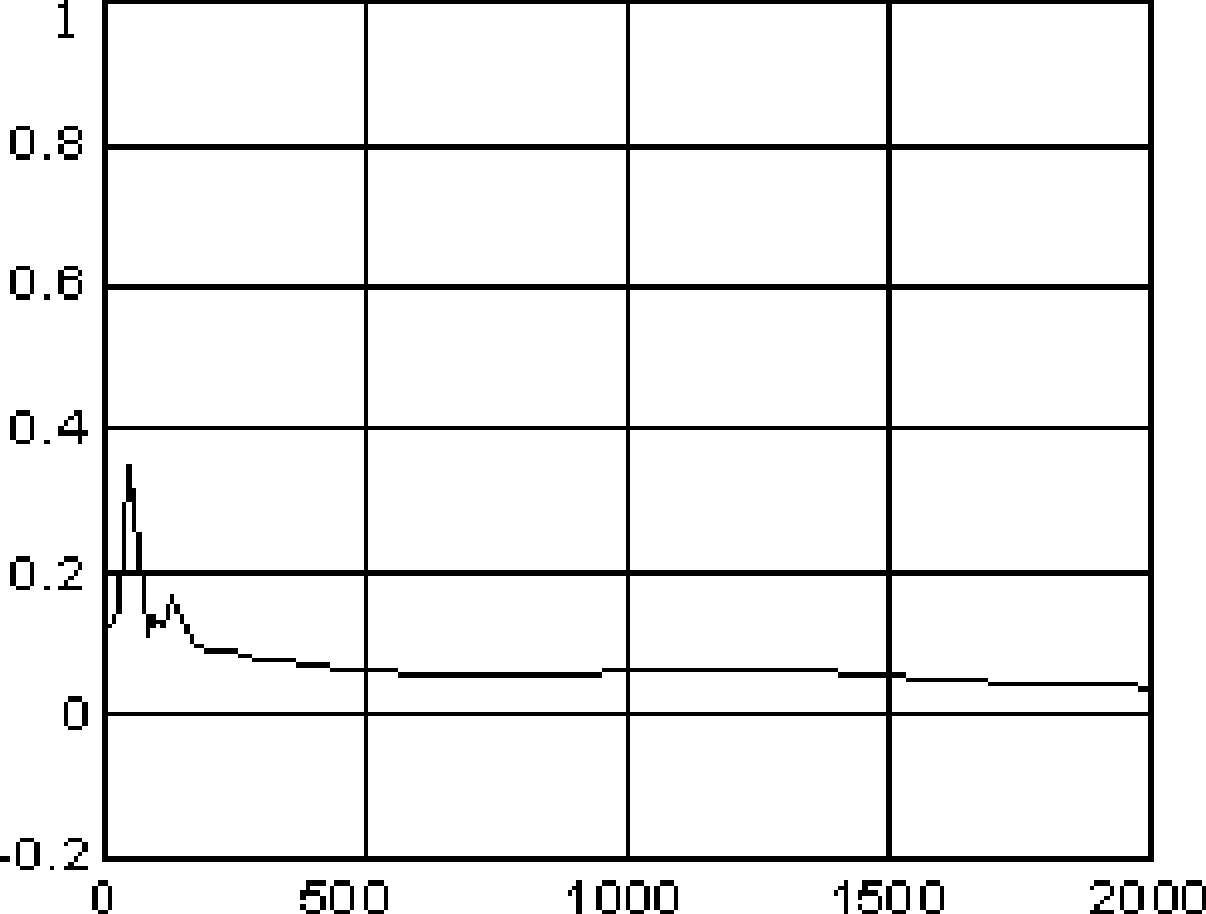
[0053] This embodiment studies the essence of solving multi-objective optimization parameters is to regard the weight coefficient in the evaluation function as a variable parameter, and then proposes a neural network based on the Lagrange function, using the calculation of the optimal weight coefficient under the condition of the least squares criterion , give appropriate parameters according to actual needs, and obtain a satisfactory and stable effective solution.

[0054] Existing model optimization methods for multi-objective optimization:

[0055] In objective optimization, record m vector objective functions as

[0056] f(x)=(f 1 (x), f 2 (x),...,f m (x)) (1)

[0057] The constraint set is denoted as

[0058] D={x: x ∈ R n , g i (x)≥0, i=1, 2, ..., p; h j (x)=1, j=1, 2, ..., q} (2)

[0059] Then the formulation of the problem is to solve

[0060] min x ∈ D f ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a Lagrange function based least-squares multi-objective optimization method which includes the steps of step 1, converting multi-objective programming into single-objective programming; step 2, fitting established models to obtain a fitting error; step 3, obtaining an optimal solution model; step 4, interposing a weighted factor beta into a target function Q(n); step 5, obtaining an extended function; step 6, removing non-negative weights from the optimal solution model; and step 7, calculating an optimal weighting coefficient by least-squares criterion. By the method, a system can evolve to the equilibrium state no matter how the initial state of the system is, a neural network can converge a variable into a unique global optimal solution no matter how an initial value of an optimized variable is.

Description

technical field [0001] The invention relates to the field of objective optimization calculation, in particular to a least-squares criterion multi-objective optimization method based on Lagrange function. Background technique [0002] When solving practical problems, in order to achieve satisfactory results, people always choose the best solution from many alternative solutions according to a certain standard. When there is only one target in the considered problem as the criterion for judging the pros and cons, this is the usual single solution. However, in order to better solve practical problems, it is more and more necessary to consider the optimization problem of multiple objectives at the same time, that is, the multi-objective optimization problem. The key to solving the multi-objective optimization problem lies in the determination of the objective weights. Multi-objective optimization methods can be widely used in optimization computing, pattern recognition, array s...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/10G06N3/02
Inventor 高俊文刘建成
Owner 高俊文
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com