Multi-sample facial expression recognition method based on low-rank tensor decomposition

A tensor decomposition and expression recognition technology, applied in the field of facial expression recognition, can solve the problems that expressions are easily affected by different individuals, and it is difficult to preserve the nonlinear characteristics of expressions, so as to improve the recognition rate of facial expressions and the ability to express them. Effect

Active Publication Date: 2019-11-29
UNIV OF ELECTRONIC SCI & TECH OF CHINA
View PDF6 Cites 6 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

That is, the same kind of expression is easily affected by different individuals, and in the research of practical application, the change information of expression features has two c

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Multi-sample facial expression recognition method based on low-rank tensor decomposition
  • Multi-sample facial expression recognition method based on low-rank tensor decomposition
  • Multi-sample facial expression recognition method based on low-rank tensor decomposition

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0016] In order to make the objectives, technical solutions, and advantages of the present invention clearer, the present invention will be further described in detail below in conjunction with the embodiments and the drawings.

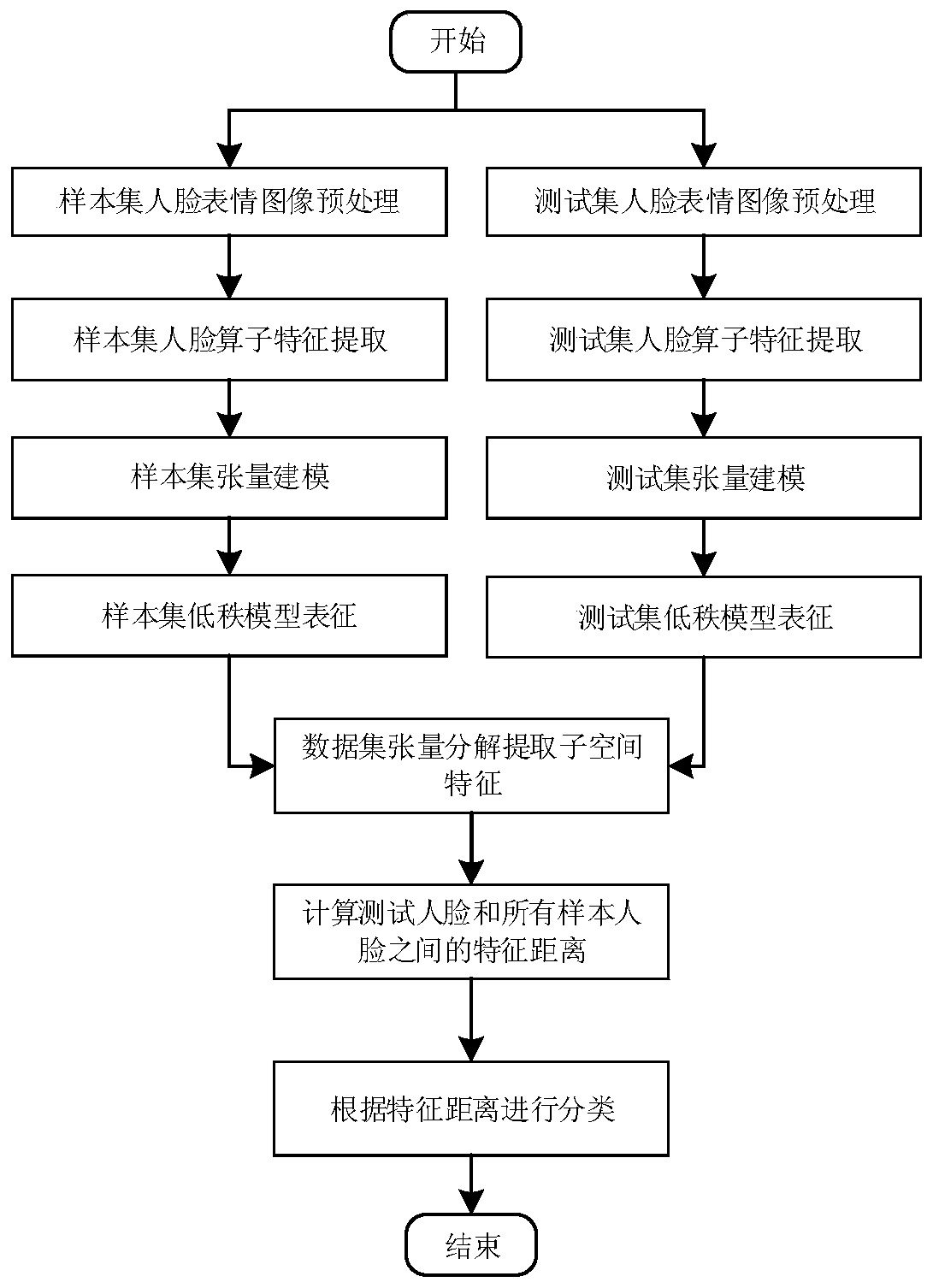
[0017] The present invention proposes a reference to the overall framework schematic diagram of a diverse face expression recognition method based on low-rank tensor decomposition figure 1 Shown.

[0018] The present invention provides a facial expression recognition method, which includes the following steps:

[0019] Perform steps S1 to S5 on the sample set and test set:

[0020] S1: Image preprocessing, using the face detection algorithm to intercept the face area in the image;

[0021] S2: Feature extraction, feature extraction of facial expression images through feature operators in multiple modes;

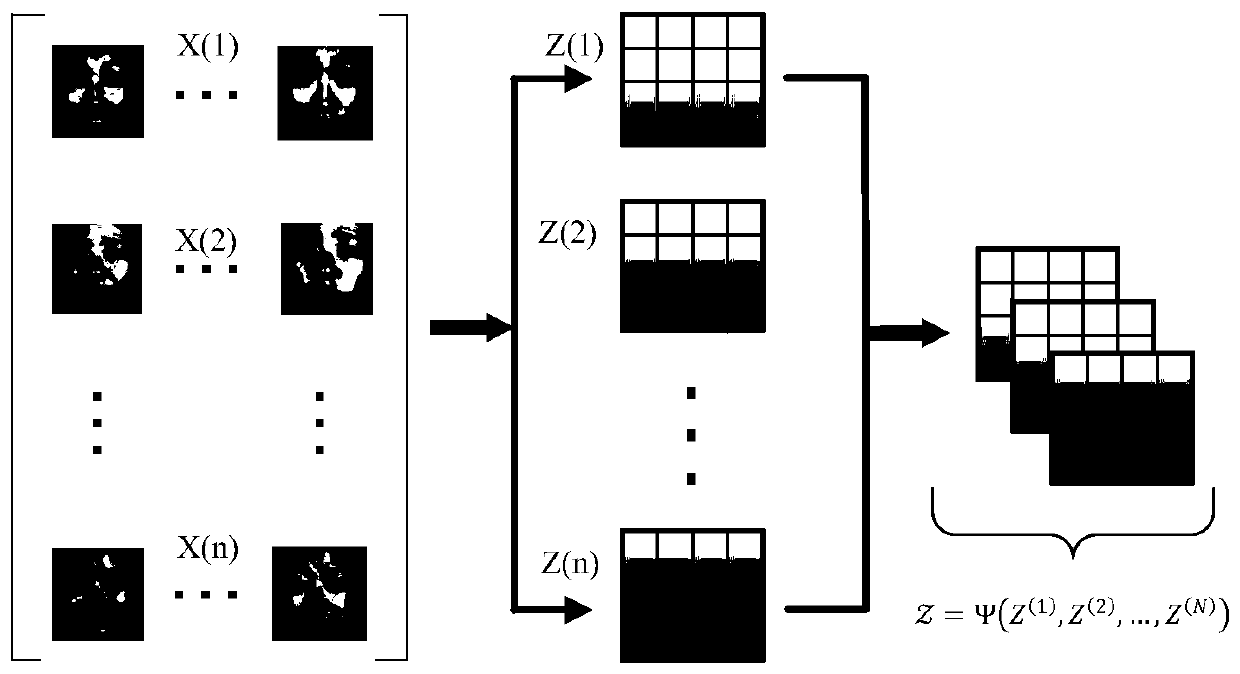
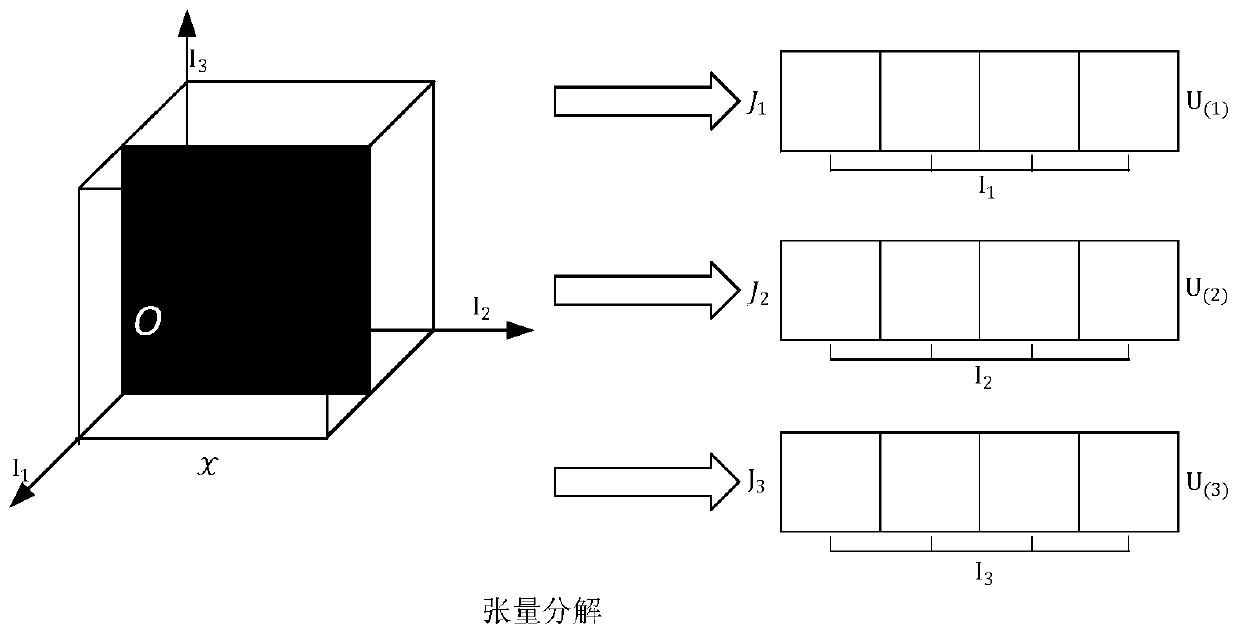
[0022] S3: Tensor modeling, according to the extracted operator features of the face region, construct a tensor model based on the operator and the experimenta...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention provides a multi-sample facial expression recognition method based on low-rank tensor decomposition. The multi-sample facial expression recognition method comprises an image preprocessing step, a feature extraction step, a tensor modeling step, a low-rank learning step, a tensor decomposition step and a feature classification step. According to the multi-sample facial expression recognition method, tensor representation feature space is utilized to reserve nonlinear features of an image; and face sub-space area features of different individuals are learned through a low-rank tensor decomposition technology, and face information under different dimensions is obtained, and tensors under all sub-spaces are decomposed, clustered and reconstructed to obtain effective expression features, and the expression information expression capacity is higher, so that the face expression recognition rate is increased.

Description

technical field [0001] The invention relates to the technical field of facial expression recognition, in particular to a method for recognizing diverse facial expressions based on low-rank tensor decomposition. Background technique [0002] In the daily communication of human beings, only 7% of the information transmitted by language is used in human facial expressions, while the information transmitted by human facial expressions is as high as 55%. Research on how computers can understand and express emotions like humans, and can adapt to the environment autonomously, will fundamentally change the connection between humans and computers. Therefore, facial expression recognition has broad application prospects. One is that it can promote the development of multiple subjects such as human-computer interaction, artificial intelligence, psychology, and computer vision, and the other is that it plays a huge role in the application of service industry, reconnaissance and basic di...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06K9/00
CPCG06V40/172G06V40/168G06V40/174
Inventor 刘欣刚李辰琦卓欣然汪卫彬
Owner UNIV OF ELECTRONIC SCI & TECH OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap