Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Structured constitution method of high enclose long low code rate multi-scale LDPC code

A technology of LDPC codes and construction methods, which is applied in the field of communication channel coding and decoding, and can solve problems such as inability to reflect superiority

Inactive Publication Date: 2008-08-27
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF0 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0009] However, the existing algebraic construction methods of multi-ary LDPC codes are limited to avoiding the occurrence of rings with a length of 4, that is, the minimum ring length can only be guaranteed to be 6. The RS code has superior performance, so only comparing the algebraically constructed multi-ary LDPC code with the RS code does not reflect the superiority of the algebraic construction of the multi-ary LDPC code and other methods of constructing LDPC codes

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Structured constitution method of high enclose long low code rate multi-scale LDPC code
  • Structured constitution method of high enclose long low code rate multi-scale LDPC code
  • Structured constitution method of high enclose long low code rate multi-scale LDPC code

Examples

Experimental program
Comparison scheme
Effect test

example 1

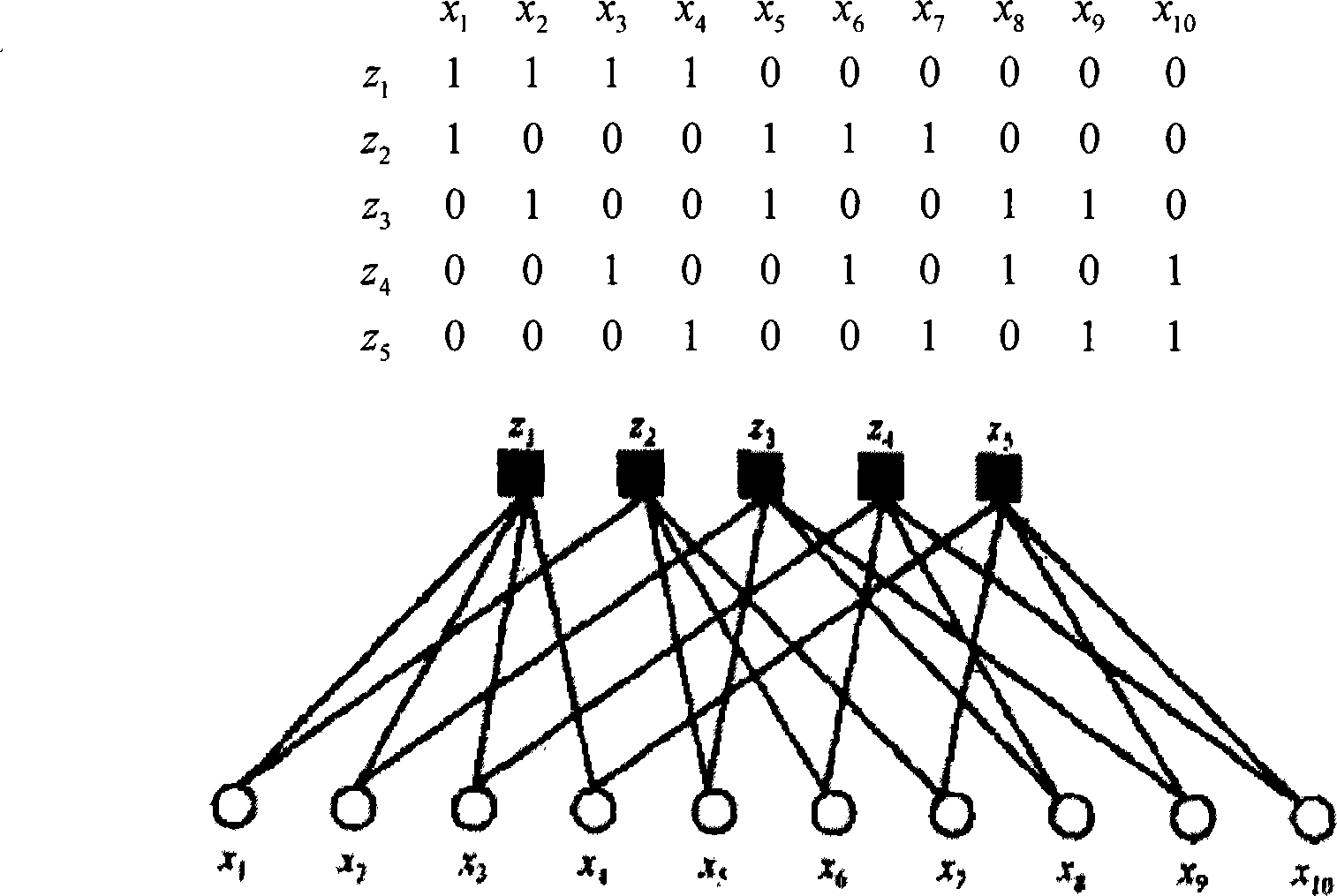
[0033] The first step select m=3, s=2, then q=2 6 = 64;

[0034] The second step is to construct the set B={1, α, α 2 , 1+α+α 2};

[0035] The third step is to construct GF(2 6 ) on the basis matrix of 256×4;

[0036] The fourth step replaces each element in the base matrix with its address vector, and the non-zero elements of the address vector use the original elements in the base matrix to obtain GF(2 6 ) on the final check matrix of 256×252. Although the parity check matrix has more rows than columns, its rank is only 175, so the LDPC code corresponding to this parity check matrix is ​​a 64-ary (252, 77) code, the code rate is 0.3056, and the column weight is 4. And the minimum ring length is 8.

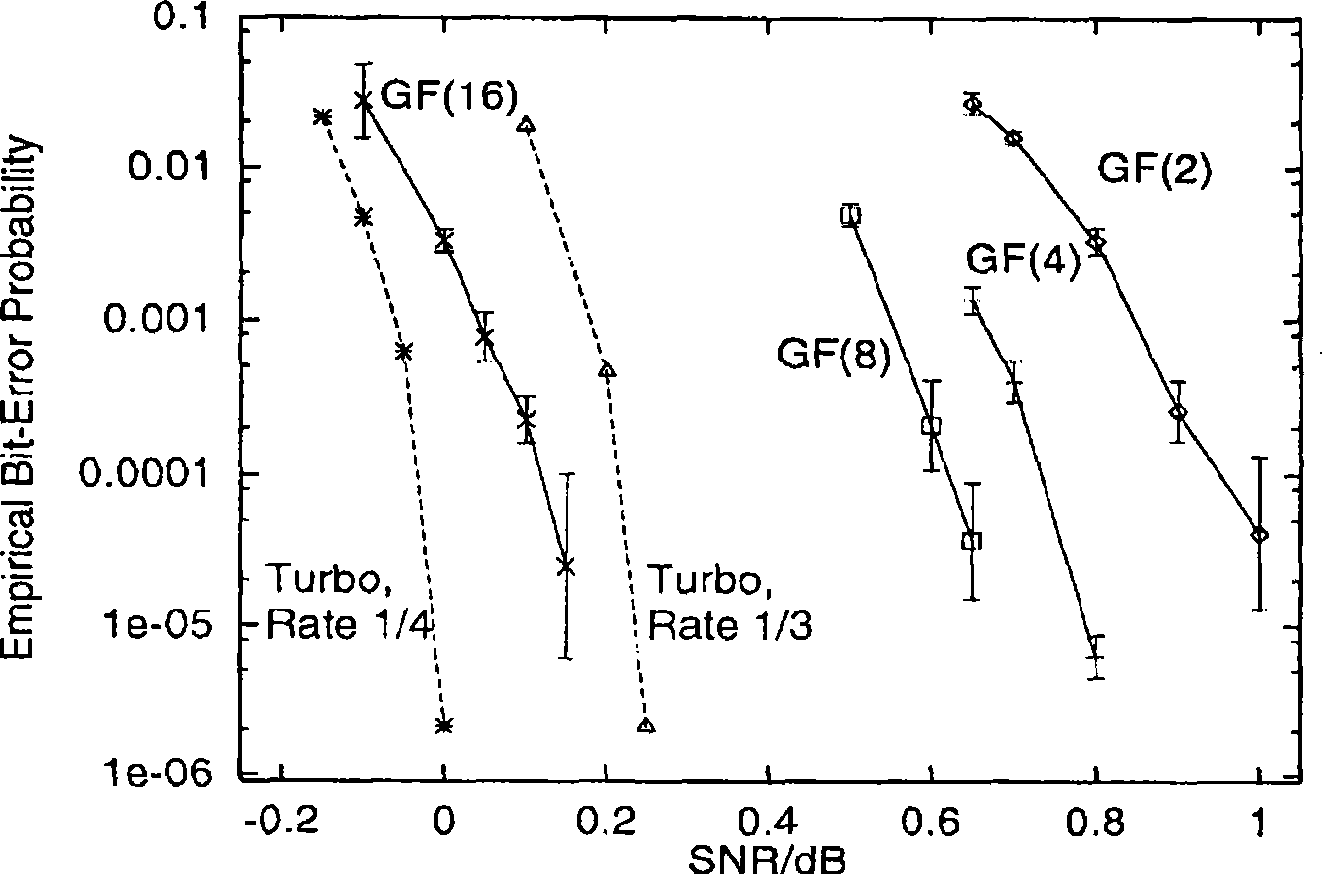
[0037] Figure 4 The performance simulation results of this code are given in , for comparison, in Figure 4 The performance simulation of Mackay random LDPC codes with the same code rate, code length, base number and column weight is also given in . It can be seen from...

example 2

[0039] The first step select m=4, s=2, then q=2 8 =256

[0040] The second step is to construct the set B={1, α, α 2 , 1+α+α 2 , 1+α+α 2 +α 3}

[0041] The third step is to construct GF(2 8 1280×4 basis matrix on )

[0042] The fourth step replaces each element in the base matrix with its address vector, and the non-zero elements of the address vector use GF(2 4 )={γ -∞ , gamma 0 , gamma 1 ,...,γ 14} in non-zero elements. The specific replacement method is as follows: the first position in the address vector corresponds to γ 0 (That is, if the non-zero element in the address vector is in the first position, set this non-zero element to γ 0 , similar to the following), the second position corresponds to γ 1 ,..., the 15th position corresponds to γ 14 , the 16th position corresponds again to γ 0 ……So on and so forth. After replacing the elements in the basis matrix with the address vector, we get GF(2 4 ) on the final parity check matrix of 1280×1024. Although...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a construction method of structured non-binary LDPC code with large girth and low bit-rate based on finite field. The method includes the following steps: 1, parameters m and s are selected; 2, a subset B of GF(2) is constructed; 3, a base matrix W is constructed on the GF(2) by taking use of the subset B; 4, each element of the base matrix W is replaced with the address vector of the element and the nary numbers of the none-zero elements of the address vector are selected according to the nary numbers of the LDPC code to be constructed; in this way the LDPC code can be constructed. The construction method of check matrices provided by the invention is capable of constructing non-binary LDPC codes with any minimum length. Simulation results show that algebraic non-binary LDPC codes constructed through the construction method are obviously improved as compared with Mackay non-binary stochastic LDPC codes with the same parameters.

Description

technical field [0001] The invention relates to a structural construction method of a multi-ary LDPC code with high girth and low code rate based on a finite field, which belongs to the field of communication channel coding and decoding, and specifically relates to a multi-ary low-density parity check code check Matrix construction method. Background technique [0002] In general, practical channels are not ideal. First of all, these channels have non-ideal frequency selection characteristics. In addition, there are noise interference and other interference mixed in when the signal is transmitted through the channel. These disturbances impair the transmitted signal and cause errors in the received digital sequence. In order to overcome these noises and interferences and increase the reliability of data transmission, or to increase the fidelity of received signals, it is often necessary to introduce some redundant bits into the information sequence. This method of increasi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H03M13/11
Inventor 刘珂珂费泽松匡镜明
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com