Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Extended target probability hypothesis density filtering method based on cubature Kalman filtering

A technology of probability hypothesis density and Kalman filtering, which is applied to instruments, character and pattern recognition, computer components, etc., can solve problems that are difficult to solve, non-linear function Jacobian matrix does not exist, etc.

Inactive Publication Date: 2014-04-16
XI'AN POLYTECHNIC UNIVERSITY
View PDF3 Cites 25 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The purpose of the present invention is to provide a kind of extended target probability hypothesis density filter method based on volumetric Kalman filter, solve the tracking problem that the non-linear function Jacobian matrix that EK-EPHD cannot handle does not exist or is difficult to solve

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Extended target probability hypothesis density filtering method based on cubature Kalman filtering
  • Extended target probability hypothesis density filtering method based on cubature Kalman filtering
  • Extended target probability hypothesis density filtering method based on cubature Kalman filtering

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

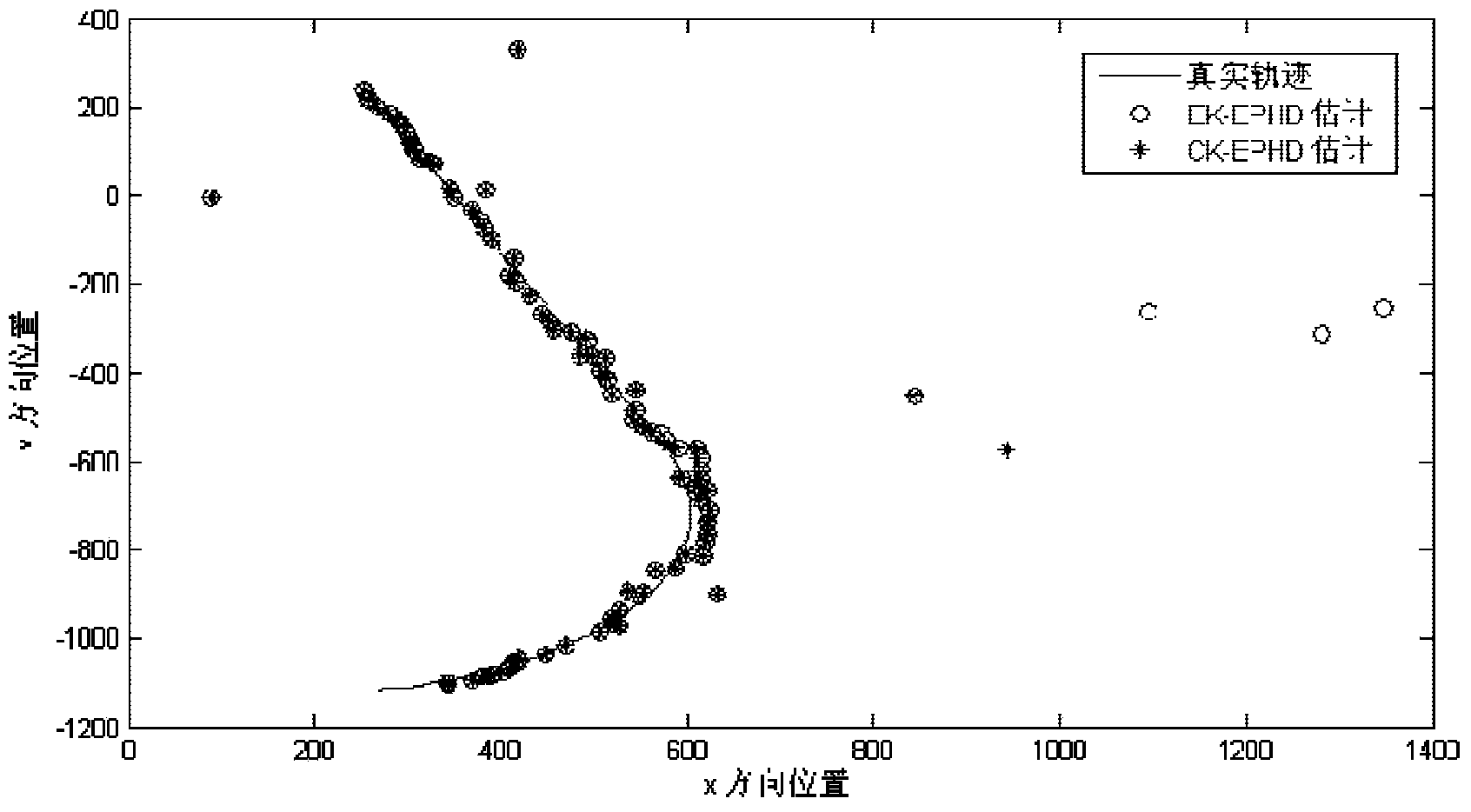
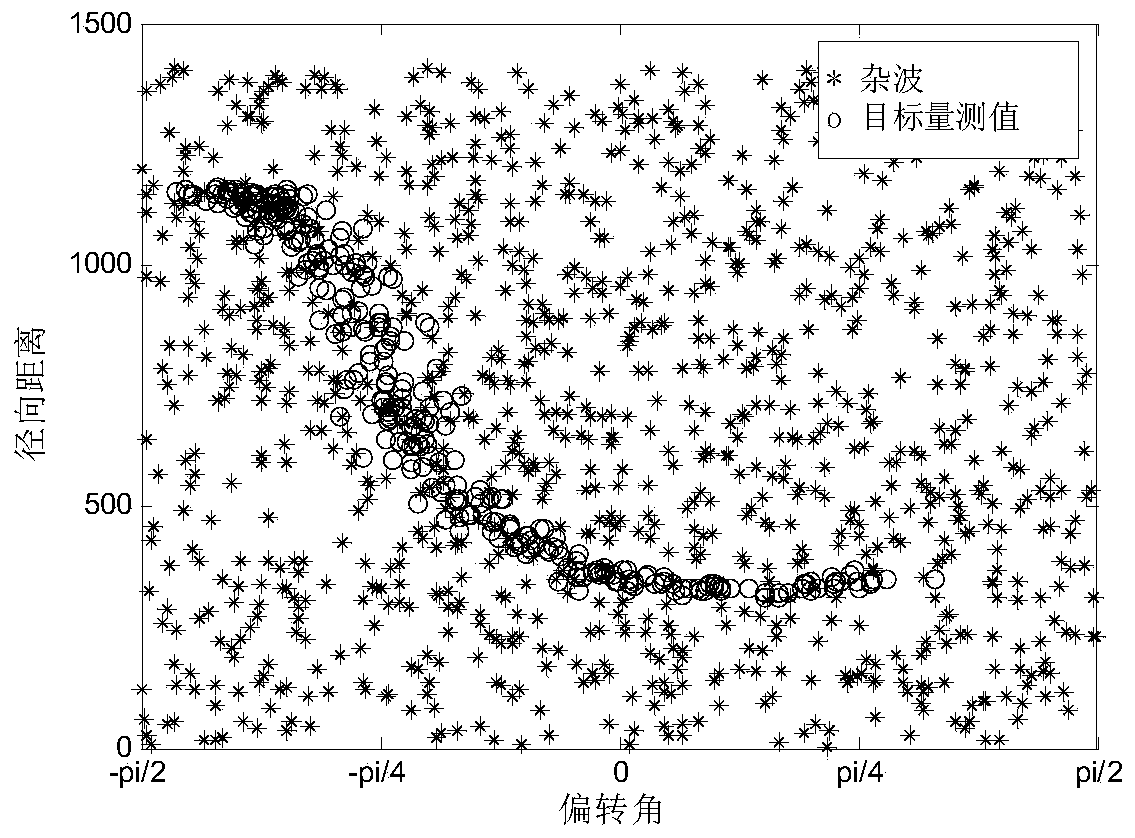
[0198] Example 1: Tracking experiment of a single extended target

[0199] The state transition equation and measurement equation of the preset target are respectively:

[0200] x k =F k x k-1 +G k ν k (33);

[0201] z k = [ arctan ( y k / x k ) x k 2 + y k 2 ] T + w k - - - ( 34 ) ;

[0202] In f...

Embodiment 2

[0219] Tracking of Multiple Extended Targets

[0220] The state transition equation and measurement equation of the target are the same as in Embodiment 1, and the parameter settings are also the same;

[0221] It is set that there are 3 targets in the entire simulation area, target 1 appears at time k=1 and dies at time k=100; target 2 appears at time k=11 and dies at time k=100; target 3 occurs at time k=66 Appears and dies at k=100 time; target 1 and target 2 both move at a constant speed, and target 3 makes a turning motion;

[0222] Let the PHD of the random set of newborn targets be:

[0223] γ k ( x ) = 0.1 N ( x ; m γ ( 1 ) , P γ ) ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an extended target probability hypothesis density filtering method based on cubature Kalman filtering. The method comprises the steps of (1) pre-setting the Gaussian mixture form of posterior strength of the moment k-1 and obtaining the mean value and covariance of the ith Gaussian item, (2) conducting one-step prediction on the weight, mean value and covariance of the ith Gaussian item obtained from the first step, and (3) conducting measurement updating on the prediction result obtained from the second step to obtain the estimated value of each Gaussian component (as stated in the specification) of the moment k. According to the extended target probability hypothesis density filtering method based on cubature Kalman filtering, extended target tracking is achieved under a nonlinear system, extended target tracking is achieved when the Jacobian matrix of a nonlinear function does not exist or is hard to solve, and a new realization approach is provided for extended target tracking under nonlinear conditions.

Description

technical field [0001] The invention belongs to the technical field of target tracking methods, and relates to an extended target probability hypothesis density filtering method, in particular to a volumetric Kalman filter-based extended target probability hypothesis density filtering method. Background technique [0002] Target tracking is the process of estimating the current state of the target based on the measurements received by the sensor. Traditional multi-target tracking methods, such as: joint data association, multi-hypothesis tracking, etc. are all based on data association. As the number of targets increases, these tracking methods will have the problem of "combination explosion" and exponential growth of calculation amount; The Probability Hypothesis Density (PHD) filtering method based on random finite sets proposed in recent years can effectively avoid the problem of data association, and can directly analyze the multi-targets in complex environments with unk...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06K9/32
Inventor 马丽丽王妮陈金广胡西民
Owner XI'AN POLYTECHNIC UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com