Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Challenge-response signatures and secure diffie-hellman protocols

A signer and independent variable technology, applied to key distribution, can solve the problem of avoiding any form of analysis

Inactive Publication Date: 2008-01-30
IBM CORP
View PDF1 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0008] However, despite its appeal and success, MQV has so far evaded any formal analysis in a well-defined model of key exchange

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Challenge-response signatures and secure diffie-hellman protocols
  • Challenge-response signatures and secure diffie-hellman protocols
  • Challenge-response signatures and secure diffie-hellman protocols

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

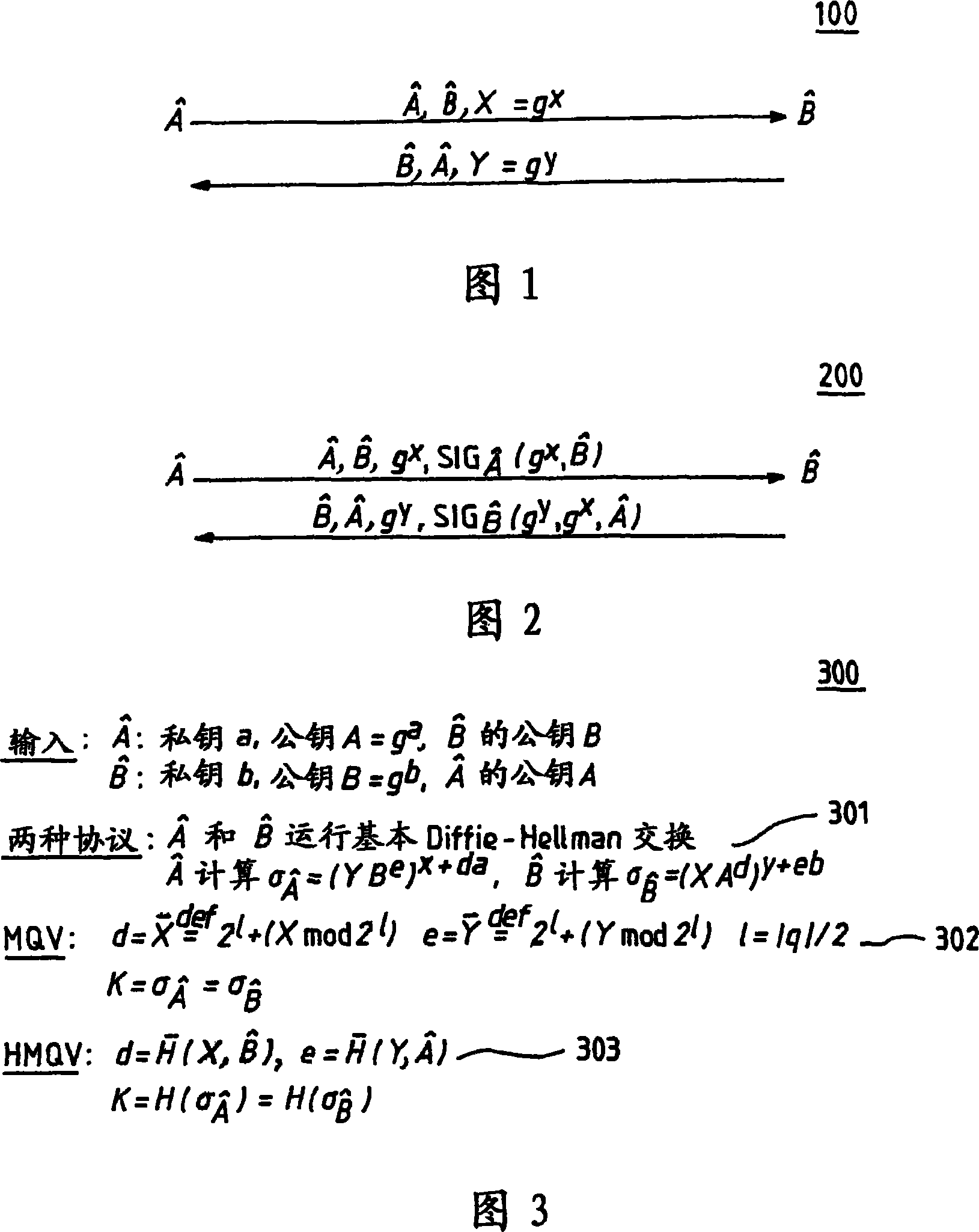
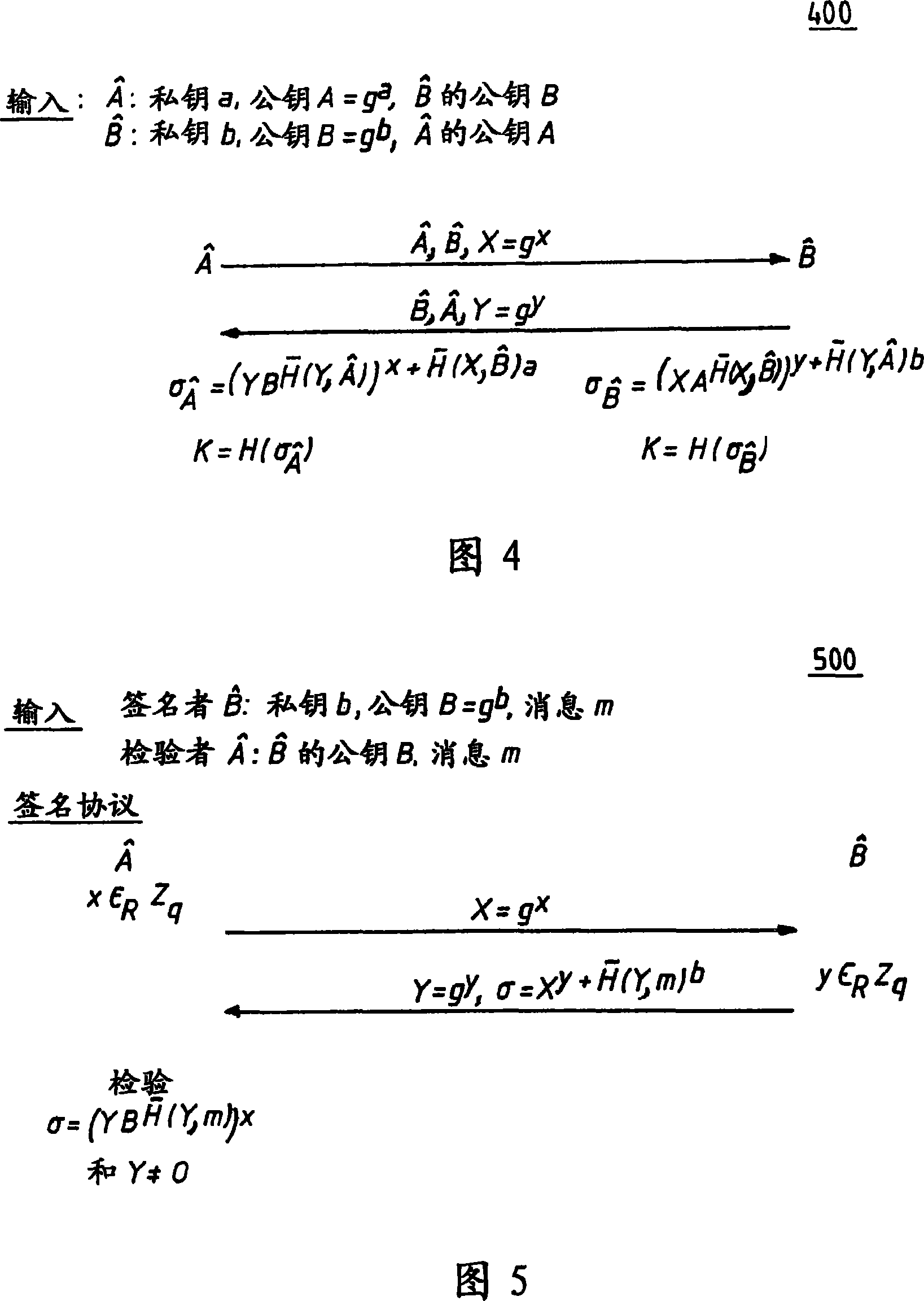
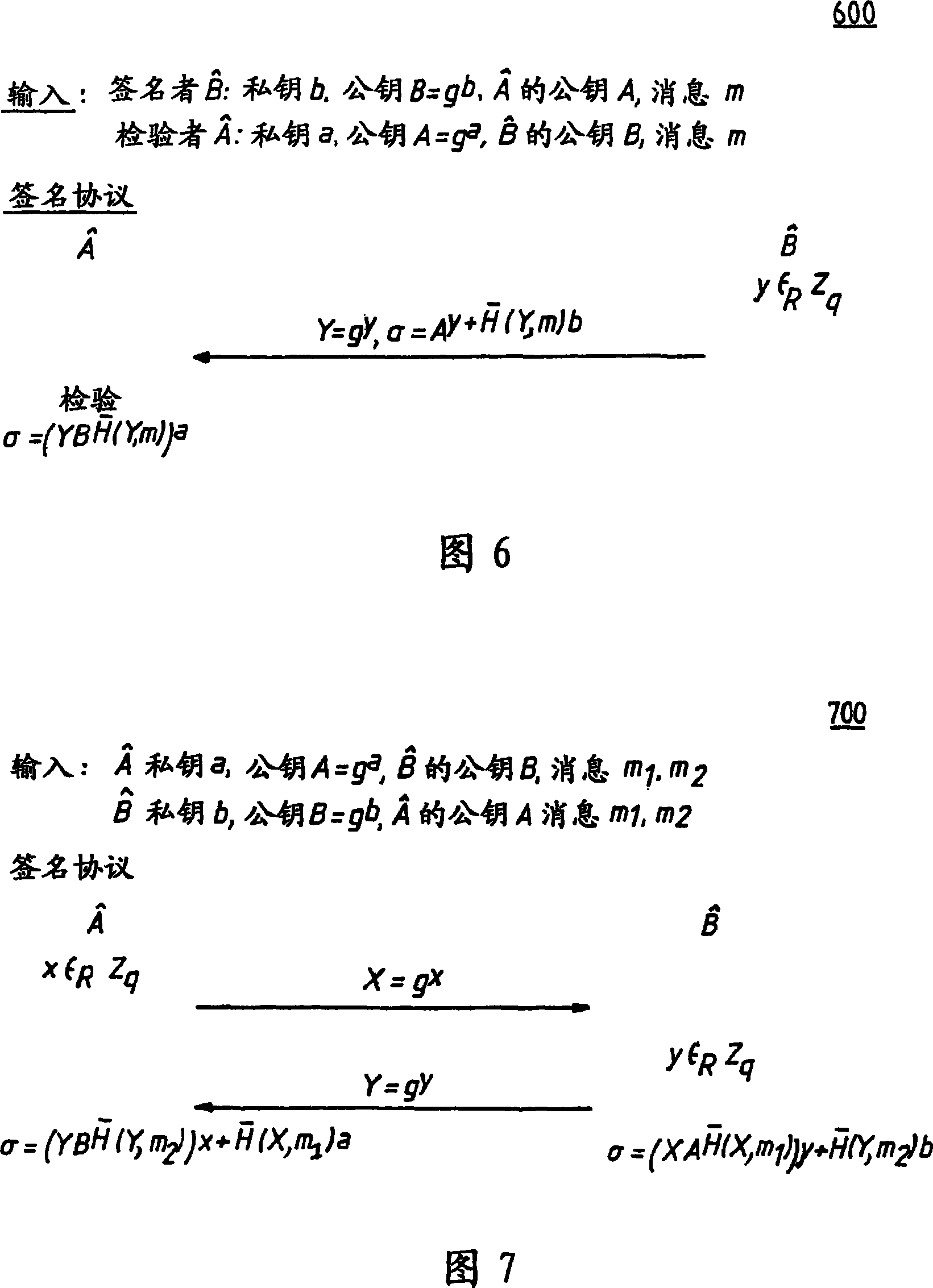
[0029] Referring now to the drawings, and more particularly to FIGS. 1-11 , there are shown exemplary embodiments of methods and structures in accordance with the present invention.

[0030] As a preliminary note on groups and notations, all protocols and operations discussed in this paper assume a cyclic group G of order q (usually prime) generated by a generator g. The bit length of q is given by |q| (eg means the logarithm of q to base 2, rounded up to the nearest integer), and this quantity is used as an implied safety parameter. For simplicity, as is common in practice, the parameters G, g and q are assumed to be fixed and known in advance by all parties. Optionally, these values ​​can be included in certificates or the like.

[0031] A multiplicative representation of group operations is used here, but the process is equally applicable to additive groups, such as elliptic curves or any other algebraic or special groups, finite fields, composite modules, etc. In the pro...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A method (and structure) of exchange between two parties interconnected by a device or network. A recipient party (verifier) chooses a secret value x for computing a value X=F1(x), where F1 comprises a first predetermined function having at least one argument, the value x being one of the at least one argument of F1. A signing party (signer) chooses a secret value y for computing a value Y=F2(y), where F2 comprises a second predetermined function having at least one argument, the value y being one of the at least one argument of F2. The signer obtains the value X, and the signer has a private key b and a public key B. The signer computes a value s=F3(y,b,X), where F3 comprises a third predetermined function having at least three arguments: the value y, the private key b, and the value X being three arguments of the at least three arguments of F3. There exists a fourth predetermined function F4(x,Y,B) to calculate a value s', F4 having at least three arguments: the value x, the value Y, and the public key B being three arguments of the at least three arguments of F4, but the value s is not an argument of F4. There exists no secret shared between the verifier and the signer that serves as a basis for any argument in any of the functions F1, F2, F3, and F4. The verifier can consider the values s and s' as valid authenticators if value s' is determined to be related in a predetermined manner to value s.

Description

technical field [0001] Aspects of the invention generally relate to signatures that are provably secure to senders and recipients of information exchanges. More specifically, challenge-response signature schemes have the property that both the verifier and the signer can compute the same or related signatures, the former by knowing the challenge and the latter by knowing the private signature key ), thereby permitting in the exemplary embodiment variants of provably secure, conventional key exchange protocols, including variants of the well-known MQV protocol. Background technique [0002] As originally suggested, the Diffie-Hellman (DH) key exchange protocol 100 shown in Figure 1 is considered secure against eavesdropping-only attackers. The search for an "authenticated Diffie-Hellman" protocol resistant to efficient, man-in-the-middle attacks has led to numerous ad-hoc (ad hoc) proposals, among them Many were damaged or showed faults. With the development of rigorous se...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/08
Inventor H·克拉夫奇克
Owner IBM CORP
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com