Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Backstepping sliding mode control method for formation flying spacecraft

A technology of formation flying and backstepping sliding mode, which is applied in the direction of attitude control, adaptive control, general control system, etc., can solve the problem of limited time coordination control of spacecraft that is difficult to expand formation flight

Active Publication Date: 2020-06-09
XIANGTAN UNIV
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, these cooperative controllers are only asymptotically stable (Wang and Xie, 2011; Thunberg et al., 2014)
[0006] Most previous research works are difficult to extend to the situation of limited-time coordinated control of formation flying spacecraft, especially when there is no exchange of control signals between adjacent vehicles

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Backstepping sliding mode control method for formation flying spacecraft
  • Backstepping sliding mode control method for formation flying spacecraft
  • Backstepping sliding mode control method for formation flying spacecraft

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

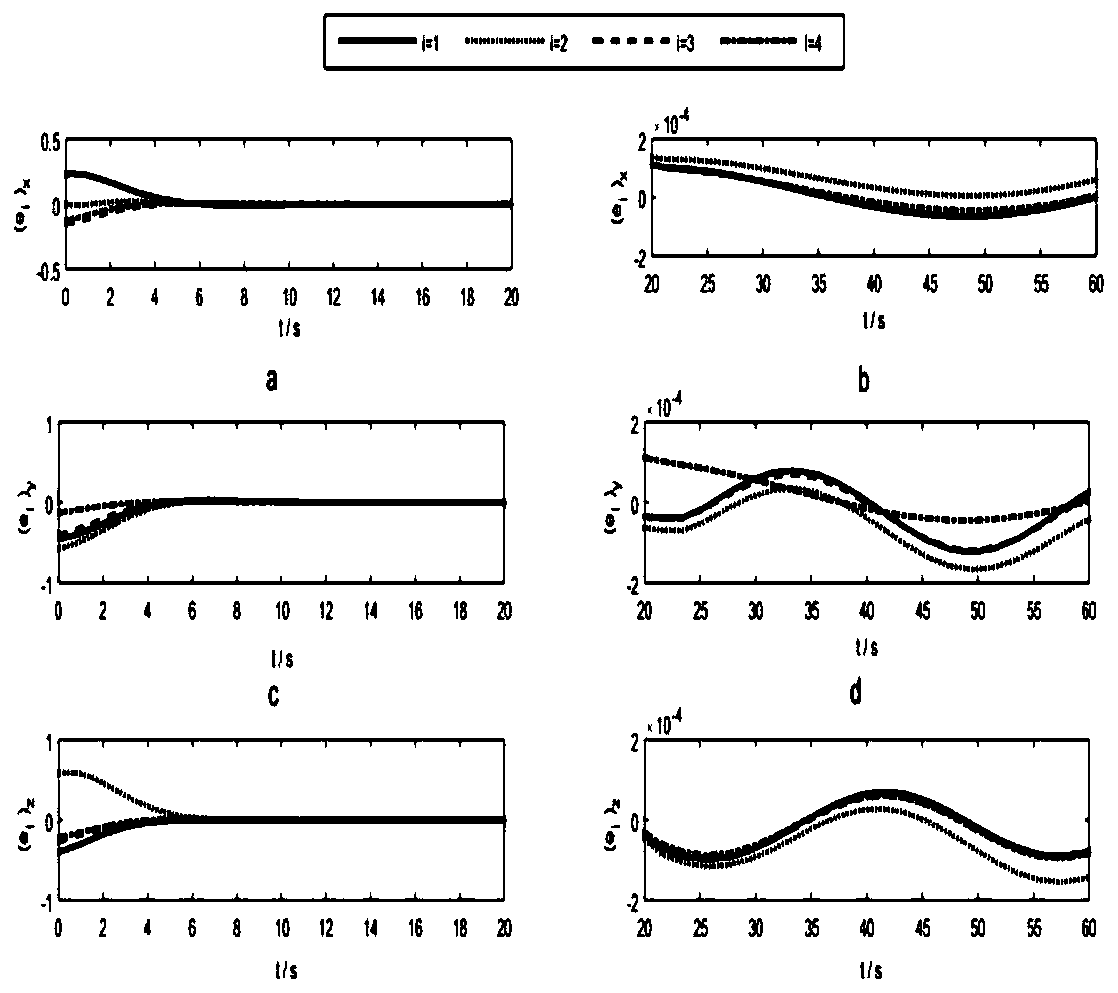
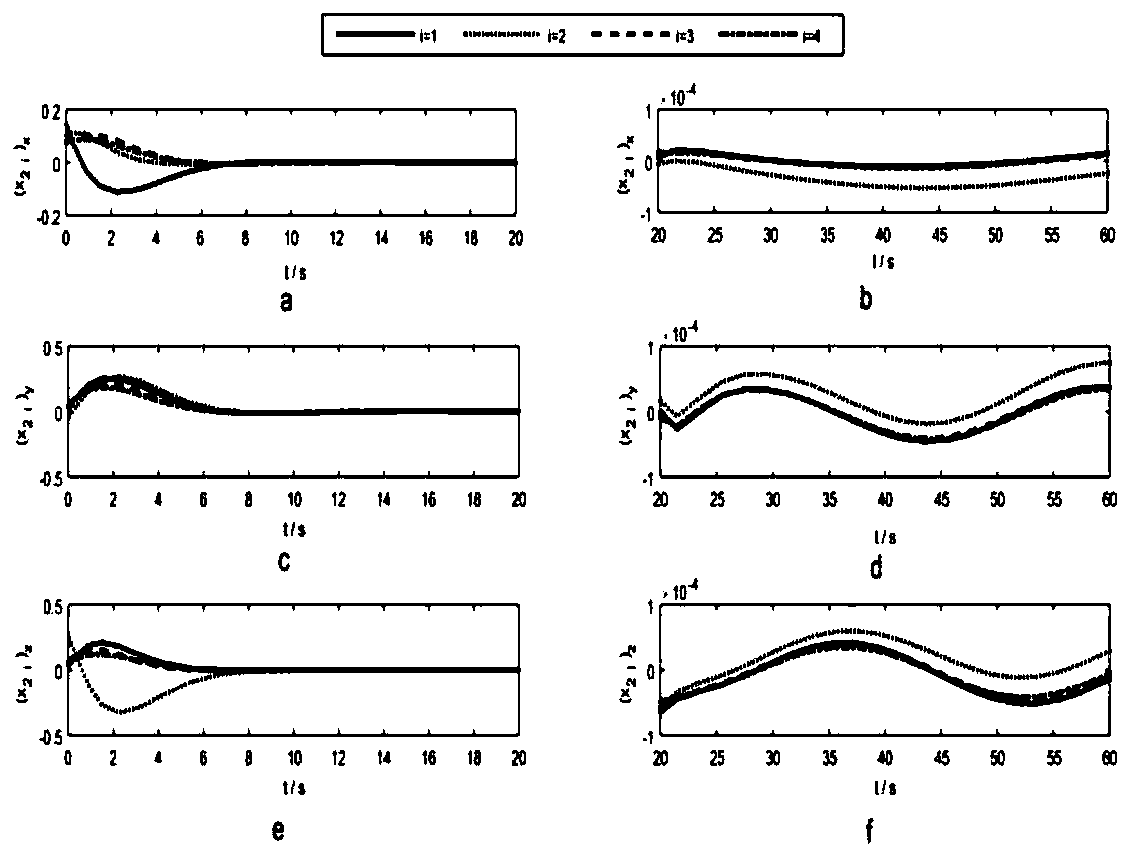
[0216] Embodiment 1 is the backstepping sliding mode control method for formation flight spacecraft for bounded external disturbances

[0217] (1) Establish the attitude dynamic model of formation flight spacecraft

[0218] Since the spacecraft is modeled as a rigid body, it is described by a rotation matrix:

[0219] R i is the rotation matrix that transforms the body coordinate system into the inertial coordinate system, ω i ∈R 3×1 is the angular velocity in the body coordinate system, u i ∈R 3×1 and d i ∈R 3×1 are the control torque and external disturbance torque, respectively, J i ∈ R 3×3 is the inertia matrix, and the dynamic equation describing the attitude of the spacecraft is as follows:

[0220]

[0221]

[0222]

[0223] (2) Introduce spacecraft attitude error

[0224] R d ∈SO(3) and ω d ∈R 3×1 is the reference attitude and angular velocity in the reference coordinate system, and are the rotation matrix error and the angular velocity error,...

Embodiment 2

[0351] Embodiment 2 For external disturbances with unknown boundaries, the backstepping sliding mode control method of formation flying spacecraft

[0352] (1) Establish the attitude dynamic model of formation flight spacecraft

[0353] Since the spacecraft is modeled as a rigid body, it is described by a rotation matrix:

[0354] R i is the rotation matrix that transforms the body coordinate system into the inertial coordinate system, ω i ∈ R 3×1 is the angular velocity in the body coordinate system, u i ∈ R 3×1 and d i ∈ R 3×1 are the control torque and external disturbance torque, respectively, J i ∈ R 3×3 is the inertia matrix, and the dynamic equation describing the attitude of the spacecraft is as follows:

[0355]

[0356]

[0357]

[0358] (2) Introduce spacecraft attitude error

[0359] R d ∈SO(3) and ω d ∈ R 3×1 is the reference attitude and angular velocity in the reference coordinate system, and are the rotation matrix error and the angula...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a formation flying spacecraft back-stepping sliding-mode control method, and belongs to the technical field of spacecraft posture adjustment. By the back-stepping sliding-modemethod, two distributed robust consistency tracking controllers are designed. The first robust controller can compensate known bounded external interface, is continuous and free from buffeting. In order to meet the use requirements of self-adaptive control, the second robust finite time controller does not need the upper bound of the known external interface. As the two controllers are designed based on a rotation matrix, attitude represented by the rotation matrix has global unique attribute, and the shortcoming of system unwinding can be overcome. By the aid of Lyapunov theorem, a whole closed-loop system is stable in finite time, simulation experiments prove that absolute attitude can be tracked, and formation member attitude consistency can be kept.

Description

technical field [0001] The invention belongs to the technical field of spacecraft attitude adjustment, and in particular relates to a backstepping sliding mode control method for formation flying spacecraft. Background technique [0002] Spacecraft formation flying (Spacecraft formation flying, SFF) can be applied to many space missions. By distributing payloads on a group of spacecraft, the formation spacecraft has the advantages of low launch cost, high flexibility, and high success rate. (Kristiansen and Nicklasson, 2009). [0003] However, due to link failure and link reconfiguration, there are problems such as communication delay and switching topology during communication link information exchange, which will deteriorate the control performance of formation aircraft. (Sun et al., 2011; Zhou and Hu, 2013) based on Lyapunov functions, a finite-time controller was given by backstepping and adding power integral terms. (Sun et al., 2011) designed a six-degree-of-freedom ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B13/04G05D1/08
Inventor 李鹏周彦兰永红盘宏斌刘勇向礼丹赵昆仑
Owner XIANGTAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com